线性代数(三) 线性方程组向量空间
前言
如何利用行列式,矩阵求解线性方程组。
线性方程组的相关概念

用矩阵方程表示
- 齐次线性方程组:Ax=0;
- 非齐次线性方程组:Ax=b.
可以理解 齐次线性方程组 是特殊的 非齐次线性方程组
如何判断线性方程组的解

- 其中R(A)表示矩阵A的秩
- B表示A的增广矩阵
- n表示末知数个数

增广矩阵

矩阵的秩



秩r<= 未知数的数量n
r=n时,称为满秩
如何求解矩阵A的秩
- 矩阵经过初等变化后秩不变
- r+1阶子式的行列式=0的特性
可以将矩阵转为化

矩阵的秩,就是矩阵初等变换后化成行阶梯形时的非零行的行数。

- 方程组的系数矩阵的秩与方程组增广矩阵的秩相等。方程组里的所有方程都是不冲突的,不会出现等式左边都是“x+y”,右边却一个是“1”,一个是“3”的情况,因为这样会得出1=3的错误等式,令方程组无解。
- 方程组的系数矩阵的秩等于未知数的个数。方程组里的方程,必须有n个是不能相互推出,这个n,便是未知数的个数。像前文举例的“x+y=2”和“2x+2y=4”,便只能属于是一个方程,因为后者可以通过前者乘以2得出。
- 当方程组的系数矩阵的秩与方程组增广矩阵的秩相等且均小于方程组中未知数个数n的时候,方程组有无穷多解。当所有的方程都不冲突,但存在一个或一个以上的方程是可以由其他方程变换过来的,这就相当于n个未知数,却没有n个方程,自然就是无穷多解了。
- 当方程组的系数矩阵的秩小于方程组增广矩阵的秩的时候,方程组无解。存在两个或多个方程有冲突,那别说了,直接无解就是了
增广矩阵求解

其计算过程还是通过消元法来解方程组。
克拉默法则
当矩阵A的行列式det(A)!=0时,可使用行列式的解方程- 克拉默法则求解
求多解

可见上述方程组的解,是一个集合,怎么表示这个集合?

基础解系
指在无穷多组解中,找到一组解,且满足:
- 这组解内的向量线性无关
- 方程组的任意一个解都可由这组向量线性表示
那么这组解(向量组),就称为基础解系
实际上这和极大线性无关组是一回事
齐次线性方程组 A x ⃗ = 0 ⃗ A\vec{x}=\vec{0} Ax=0的基础解系为
a ⃗ = ( − 1 , − 2 , 1 ) T \vec{a}=(-1,-2, 1)^T a=(−1,−2,1)T
通解为
x ⃗ = k 1 ∗ a ⃗ \vec{x}=k_1*\vec{a} x=k1∗a
其中: k 1 k_1 k1取任意常数
通解就是线性方程组解的具体表达方式
向量组



如果R(A)=m,则表示有解。即得不出上述 y = − z y=-z y=−z y和z变量的相关性

线性方程组的解的结构
所谓线性方程组的解的结构,就是当线性方程组有无限多个解时,解与解之间的相互关系.
当方程组存在唯一解时,无须讨论解的结构
基础解系给出解空间的一组基 而基的线性组合为通解。所以通解就是 基础解系前面乘于个任意数k

向量空间

定义:所谓封闭,是指集合中任意两个元素作某一运算得到的结果仍属于该集合.
如果向量空间 V 的非空子集合 V1 对于 V 中所定义的加法及乘数两种运算是封闭的,则称 V1 是 V 的子空间.
向量容量的基

- 原来方程组的多解,在空间中其反应的是一个线,面,立方的区域(方程组的维度而决定)。
- 方程的基解,即基向量。
主要参考
《如何理解矩阵的「秩」?》
《线性方程组在什么时候有唯一解/无穷个解/无解?》
《11.2 齐次线性方程组的基础解系和通解》
《线性代数之——向量空间》
相关文章:

线性代数(三) 线性方程组向量空间
前言 如何利用行列式,矩阵求解线性方程组。 线性方程组的相关概念 用矩阵方程表示 齐次线性方程组:Ax0;非齐次线性方程组:Axb. 可以理解 齐次线性方程组 是特殊的 非齐次线性方程组 如何判断线性方程组的解 其中R(A)表示矩阵A的…...

学习跨度级交互以提取方面情感三元组
方面情感三元组 方面情感三元组(Aspect Sentiment Triplet)是一种在情感分析中使用的结构,它包含三个部分:方面目标(Aspect Target)、情感(Sentiment)和对应的观点词(Op…...
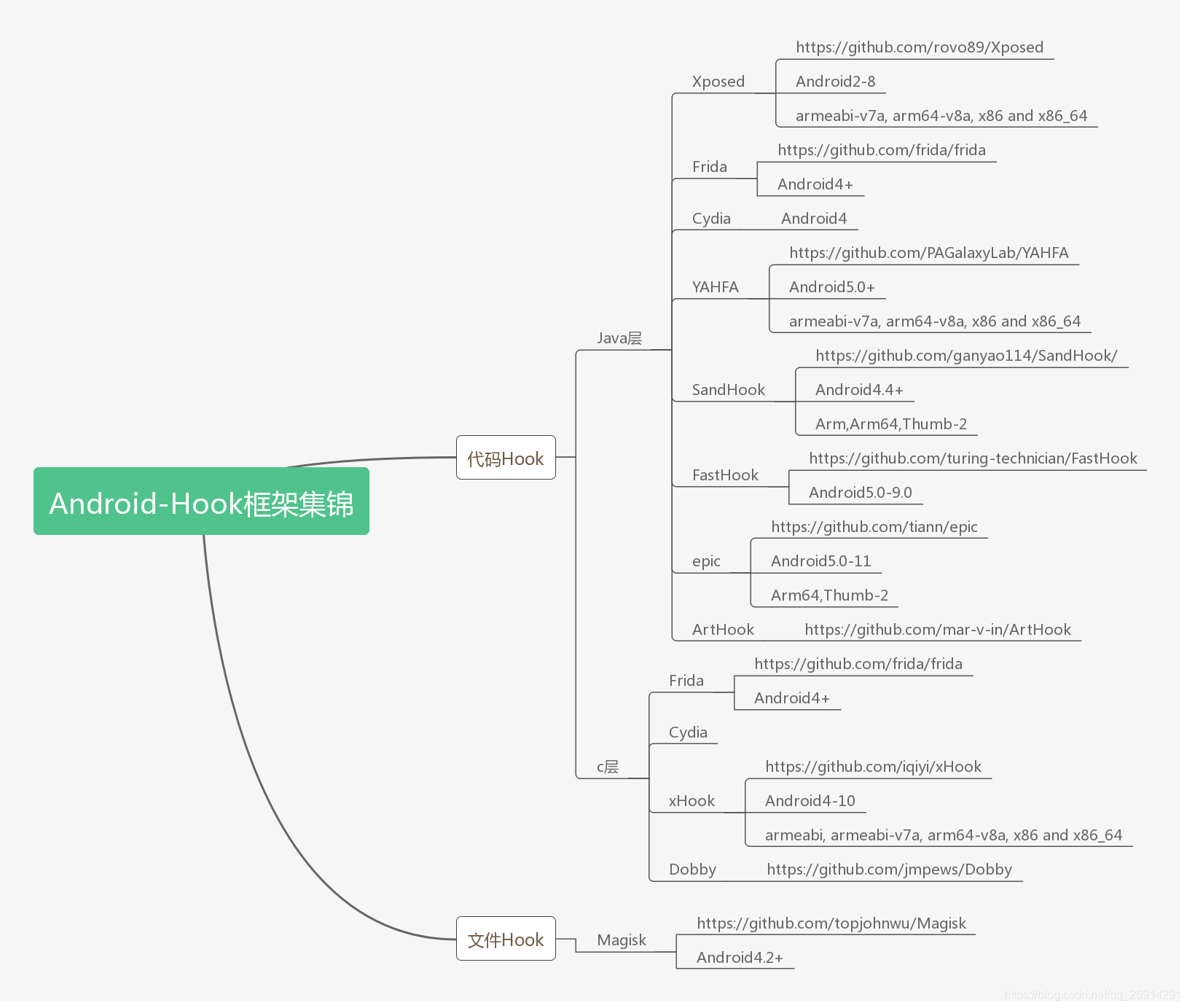
那些年的Xposed开发经验记录
把之前写的Xposed相关文章合并到一块,方便查阅 目录 多进程App的Hook问题XposedHelper中的静态变量demo的AndroidManifest.xml的测试核心代码结论限制handleLoadPackage被单个进程多次执行的问题 多dex Hook问题为应用增加权限利用Xposed删除权限参考 Hook框架集锦…...
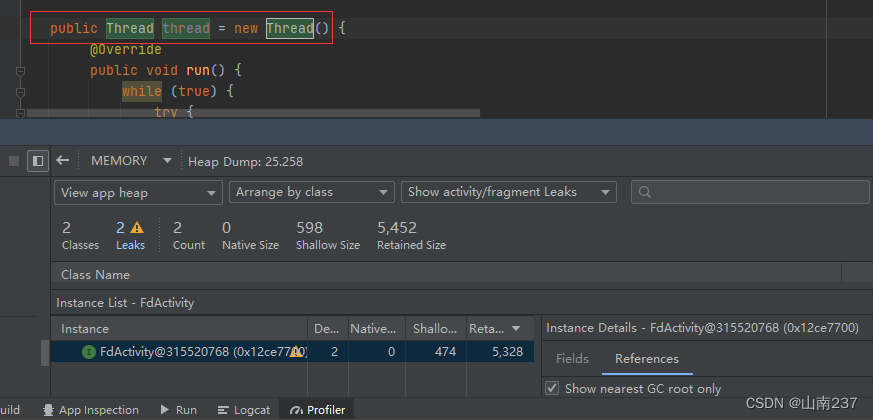
android studio内存分析之Memory profiler的使用
目录 Android Studio中内存分析工具Memory profiler的使用1. 打开Memory Profiler2. 工具使用3. 内存选项说明4. 内存性能分析器概览5. 内存计算方式6. 查看内存分配7. 捕获java/kotlin方式查看内存分配8. 堆转储文件导入和导出 内存性能分析器中的泄漏检测 Android Studio中内…...

Qt下载慢/无法下载解决方式
文章目录 一. Qt在线安装下载二. 安装方式 一. Qt在线安装下载 官网下载:https://www.qt.io/download清华源下载:https://mirrors.tuna.tsinghua.edu.cn/qt/official_releases/online_installers/ 二. 安装方式 进入下载好的目录 在目录栏输入CMD&…...
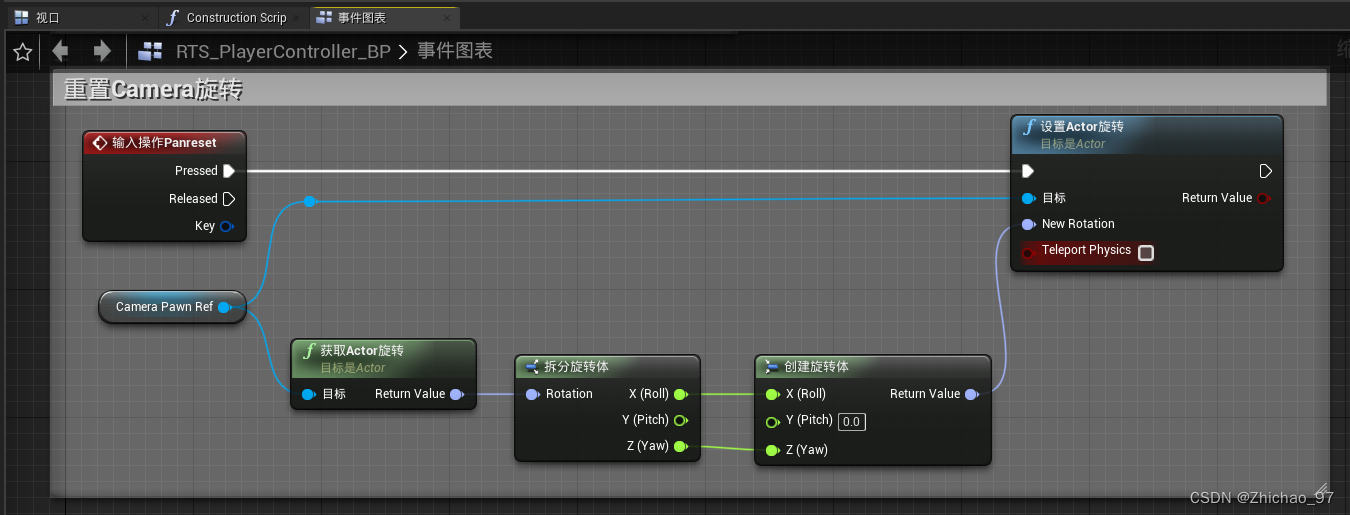
【UE4 RTS】04-Camera Pan
前言 本篇实现了CameraPawn的旋转功能。 效果 步骤 1. 打开项目设置,添加两个操作映射 2. 打开玩家控制器“RTS_PlayerController_BP”,新建一个浮点型变量,命名为“PanSpeed” 在事件图表中添加如下节点 此时运行游戏可以发现当鼠标移动…...

出现raise NotImplementedError报错
在学习《动手学深度学习》时,实现下面代码时,报出raise NotImplementedError错误。 import collections import torch from d2l import torch as d2l import math from torch import nnclass Seq2SeqEncoder(d2l.Encoder):def __init__(self,vocab_size,…...
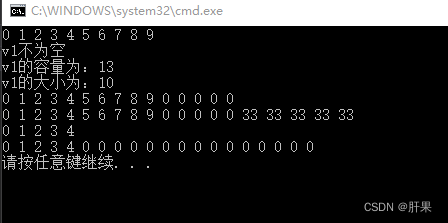
第一百二十二天学习记录:C++提高:STL-vector容器(上)(黑马教学视频)
vector基本概念 功能: vector数据结构和数组非常相似,也称为单端数组 vector与普通数组区别: 不同之处在于数组是静态空间,而vector可以动态扩展 动态扩展: 并不是在原空间之后续接新的空间,而是找更大的内…...

《Linux从练气到飞升》No.11 初识操作系统
🕺作者: 主页 我的专栏C语言从0到1探秘C数据结构从0到1探秘Linux菜鸟刷题集 😘欢迎关注:👍点赞🙌收藏✍️留言 🏇码字不易,你的👍点赞🙌收藏❤️关注对我真的…...

什么是 XSS 攻击?
概念 XSS 攻击指的是跨站脚本攻击,是一种代码注入攻击。攻击者通过在网站注入恶意脚本,使之在用户的浏览器上运行,从而盗取用户的信息如 cookie 等。 XSS 的本质是因为网站没有对恶意代码进行过滤,与正常的代码混合在一起了&…...
基于Spring Boot的招聘网站的设计与实现(Java+spring boot+MySQL)
获取源码或者论文请私信博主 演示视频: 基于Spring Boot的招聘网站的设计与实现(Javaspring bootMySQL) 使用技术: 前端:html css javascript jQuery ajax thymeleaf 微信小程序 后端:Java springboot框…...

中级课程——CSRF
文章目录 案例原理挖掘 案例 原理 挖掘 挖掘详情 首先就是对目标敏感部位进行抓包分析,比如修改信息、转账、添加信息等等。通常一个数据包HTTP请求头里边都会有一个Referer,这个需要特别去验证。比如放到Burpsuit Repeater里边去测试:去掉…...
面试热题(岛屿数量)
给你一个由 1(陆地)和 0(水)组成的的二维网格,请你计算网格中岛屿的数量。 岛屿总是被水包围,并且每座岛屿只能由水平方向和/或竖直方向上相邻的陆地连接形成。 此外,你可以假设该网格的四条边均…...
GCC获取码率后的分配)
【WebRTC---源码篇】(二十四)GCC获取码率后的分配
RtpTransportControllerSend::PostUpdates 配置码率 GoogCcNetworkController::GetPacingRates pacing_factor_默认2.5。也就是说pacer发送报文的码率是探测码率的2.5倍。 PacerConfig GoogCcNetworkController::GetPacingRates(Timestamp at_time) const {// Pacing rate …...
数据可视化工具LightningChart .NET正式发布v10.5.1——拥有全新的3D新功能
LightningChart.NET完全由GPU加速,并且性能经过优化,可用于实时显示海量数据-超过10亿个数据点。 LightningChart包括广泛的2D,高级3D,Polar,Smith,3D饼/甜甜圈,地理地图和GIS图表以及适用于科学…...

AWS认证SAA-C03每日一题
本题库由云计算狂魔微信公众号分享。 【SAA-C03助理级解决方案架构师认证】A company has a multi-tier application that runs six front-end web servers in an Amazon EC2 Auto Scaling group in a single Availability Zone behind an Application Load Balancer(ALB).A …...
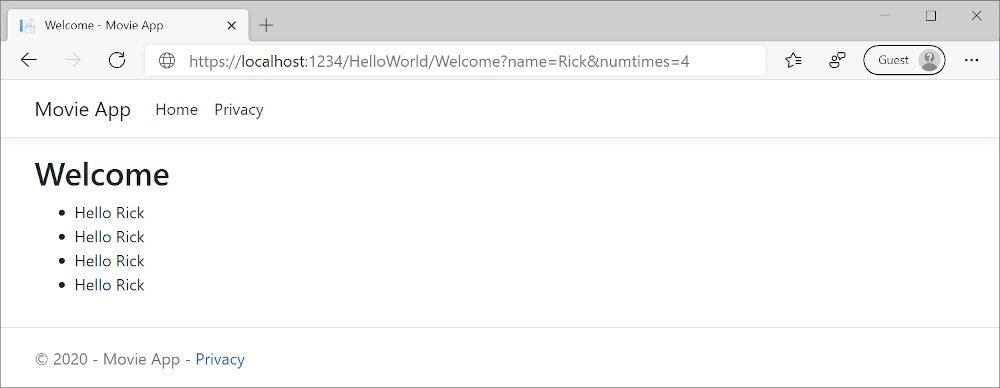
ASP.NET Core MVC -- 将视图添加到 ASP.NET Core MVC 应用
Index页 右键单击“视图”文件夹,然后单击“添加”>>“新文件夹”,并将文件夹命名为“HelloWorld”。 右键单击“Views/HelloWorld”文件夹,然后单击“添加”>“新项”。 在“添加新项 - MvcMovie”对话框中: 在右上…...
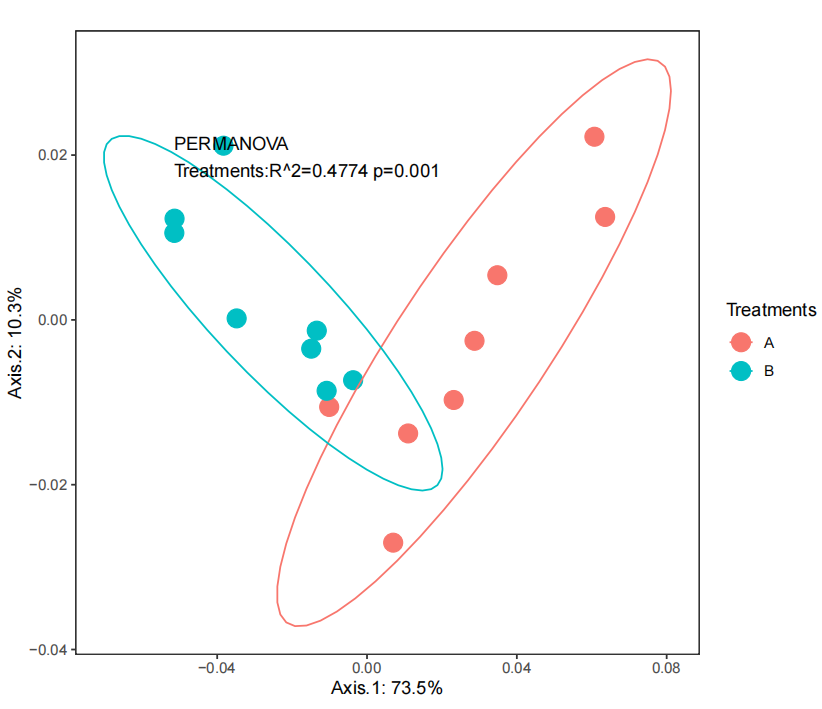
基于R做宏基因组结果的PCoA分析
写在前面 因为公司给的PCA结果效果不佳,决定从中重新挑选部分样本进行再分析 步骤 表格结果预处理 在属水平genus参考原本结果已有的PCA图,尽可能挑选距离较远且聚团的样本 选取不同样本属水平的丰度数据,整理成逗号分隔的csv文件 代码…...

8.10 算法刷题【1道题】
8.10 算法刷题 22. 链表中环的入口结点(快慢指针) 22. 链表中环的入口结点(快慢指针) 原题链接 /*** Definition for singly-linked list.* struct ListNode {* int val;* ListNode *next;* ListNode(int x) : val(x…...
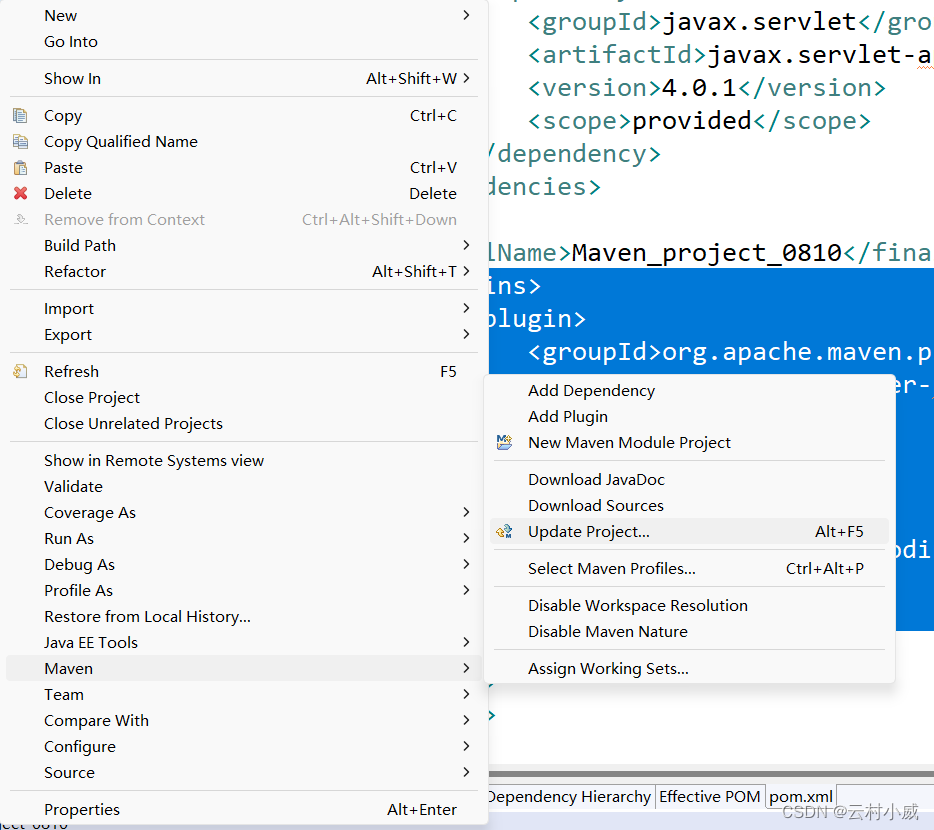
Apache Maven:从构建到部署,一站式解决方案
目录 一、Maven介绍 1. Maven是什么? 2.Maven的作用? 二、Maven仓库介绍 2.1 库的分类 三、Maven安装与配置 3.1 Maven安装 3.2 Maven环境配置 3.3 仓库配置 四、Eclipse与Maven配置 五、Maven项目测试 5.1 新建Maven项目步骤及注意事项 5.…...

AI-调查研究-01-正念冥想有用吗?对健康的影响及科学指南
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

【kafka】Golang实现分布式Masscan任务调度系统
要求: 输出两个程序,一个命令行程序(命令行参数用flag)和一个服务端程序。 命令行程序支持通过命令行参数配置下发IP或IP段、端口、扫描带宽,然后将消息推送到kafka里面。 服务端程序: 从kafka消费者接收…...

【WiFi帧结构】
文章目录 帧结构MAC头部管理帧 帧结构 Wi-Fi的帧分为三部分组成:MAC头部frame bodyFCS,其中MAC是固定格式的,frame body是可变长度。 MAC头部有frame control,duration,address1,address2,addre…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个生活电费的缴纳和查询小程序
一、项目初始化与配置 1. 创建项目 ohpm init harmony/utility-payment-app 2. 配置权限 // module.json5 {"requestPermissions": [{"name": "ohos.permission.INTERNET"},{"name": "ohos.permission.GET_NETWORK_INFO"…...

莫兰迪高级灰总结计划简约商务通用PPT模版
莫兰迪高级灰总结计划简约商务通用PPT模版,莫兰迪调色板清新简约工作汇报PPT模版,莫兰迪时尚风极简设计PPT模版,大学生毕业论文答辩PPT模版,莫兰迪配色总结计划简约商务通用PPT模版,莫兰迪商务汇报PPT模版,…...

C# 表达式和运算符(求值顺序)
求值顺序 表达式可以由许多嵌套的子表达式构成。子表达式的求值顺序可以使表达式的最终值发生 变化。 例如,已知表达式3*52,依照子表达式的求值顺序,有两种可能的结果,如图9-3所示。 如果乘法先执行,结果是17。如果5…...

Oracle11g安装包
Oracle 11g安装包 适用于windows系统,64位 下载路径 oracle 11g 安装包...

nnUNet V2修改网络——暴力替换网络为UNet++
更换前,要用nnUNet V2跑通所用数据集,证明nnUNet V2、数据集、运行环境等没有问题 阅读nnU-Net V2 的 U-Net结构,初步了解要修改的网络,知己知彼,修改起来才能游刃有余。 U-Net存在两个局限,一是网络的最佳深度因应用场景而异,这取决于任务的难度和可用于训练的标注数…...

git: early EOF
macOS报错: Initialized empty Git repository in /usr/local/Homebrew/Library/Taps/homebrew/homebrew-core/.git/ remote: Enumerating objects: 2691797, done. remote: Counting objects: 100% (1760/1760), done. remote: Compressing objects: 100% (636/636…...

快速排序算法改进:随机快排-荷兰国旗划分详解
随机快速排序-荷兰国旗划分算法详解 一、基础知识回顾1.1 快速排序简介1.2 荷兰国旗问题 二、随机快排 - 荷兰国旗划分原理2.1 随机化枢轴选择2.2 荷兰国旗划分过程2.3 结合随机快排与荷兰国旗划分 三、代码实现3.1 Python实现3.2 Java实现3.3 C实现 四、性能分析4.1 时间复杂度…...

