面试热题(岛屿数量)
给你一个由
'1'(陆地)和'0'(水)组成的的二维网格,请你计算网格中岛屿的数量。岛屿总是被水包围,并且每座岛屿只能由水平方向和/或竖直方向上相邻的陆地连接形成。
此外,你可以假设该网格的四条边均被水包围。
输入:grid = [["1","1","1","1","0"],["1","1","0","1","0"],["1","1","0","0","0"],["0","0","0","0","0"] ] 输出:1
这种题型一般都是按照dfs进行遍历查找,因为一个位置上有8种选择

所以我们应该提前的声明两个数组,一个数组中放x坐标,一个数组放y坐标
//设置方向 上右下左int[] xnum={-1,0,1,0};int[] ynum={0,1,0,-1};
我觉得这东西和扫雷是一个性质

将雷区看做是水域,数字区看成是我们的陆地,以当前节点为中心,往周围漫射(一条路走到底),但是如果
如果我们从A点到B点,如果不加限制的话,我们同样也能从B点到A点,这样就有可能能造成死循环,或者使得最后的效率变慢,所以我们可以采用两种方式
第一种方式:额外的维护一个visited数组,对访问过的地域进行标记
visited=new boolean[row][column];第二种方式:将访问过的陆地给填充成海域,不需要其他额外的操作
grid[i][j]='0';如果还不理解题,还可以这样想,假如题目数组中1组成的是由纯净水的组成的管道,我们每次遍历一个地点就是相当于给这些管道中滴了一滴红墨水,红墨水随着水的流动性,不一会这条管道中的纯净水都会变成红颜色的水
//相当于滴红墨水,需要知道该地点的坐标
private void dfs(char[][] grid, int x, int y) {} //如果是碰到水域,则停止遍历if(grid[x][y]=='0'){return;}//是陆地且没有被访问过,进行访问,并以该地点为中心,漫射if(grid[x][y]=='1'&&!visited[x][y]){visited[x][y]=true;//对于漫射的8种选择for (int i = 0; i <4; i++) {int newx=x+xnum[i];int newy=y+ ynum[i];//越界情况直接继续,不需要执行if(newx<0||newx>=row||newy<0||newy>=column||visited[newx][newy]){continue;}dfs(grid,newx,newy);}在判断是否是一个新的岛屿,肯定需要满足两个条件:1.是陆地 2.没有被访问过
//开始连接的岛屿,第一个if(!visited[i][j]&&grid[i][j]=='1'){count++;}碰到新的陆地后,再进行重复的操作
dfs(grid,i,j);好了,这道题的原理已经讲完,希望对大家能对这道题有一个比较深刻的印象
源码如下:
//设置方向 上右下左int[] xnum={-1,0,1,0};int[] ynum={0,1,0,-1};boolean[][] visited;int row;int column;public int numIslands(char[][] grid) {//对入参进行判断if(grid==null||grid.length==0||grid[0].length==0){return 0;}int count=0;//从每一个点都开始进行遍历row=grid.length;column=grid[0].length;visited=new boolean[row][column];for (int i = 0; i <row; i++) {for (int j = 0; j <column; j++) {//开始连接的岛屿,第一个if(!visited[i][j]&&grid[i][j]=='1'){count++;dfs(grid,i,j);}}}return count;}private void dfs(char[][] grid, int x, int y) {//如果是碰到水域,则停止遍历if(grid[x][y]=='0'){return;}if(grid[x][y]=='1'&&!visited[x][y]){visited[x][y]=true;for (int i = 0; i <4; i++) {int newx=x+xnum[i];int newy=y+ ynum[i];if(newx<0||newx>=row||newy<0||newy>=column||visited[newx][newy]){continue;}dfs(grid,newx,newy);}}}
相关文章:

面试热题(岛屿数量)
给你一个由 1(陆地)和 0(水)组成的的二维网格,请你计算网格中岛屿的数量。 岛屿总是被水包围,并且每座岛屿只能由水平方向和/或竖直方向上相邻的陆地连接形成。 此外,你可以假设该网格的四条边均…...
GCC获取码率后的分配)
【WebRTC---源码篇】(二十四)GCC获取码率后的分配
RtpTransportControllerSend::PostUpdates 配置码率 GoogCcNetworkController::GetPacingRates pacing_factor_默认2.5。也就是说pacer发送报文的码率是探测码率的2.5倍。 PacerConfig GoogCcNetworkController::GetPacingRates(Timestamp at_time) const {// Pacing rate …...
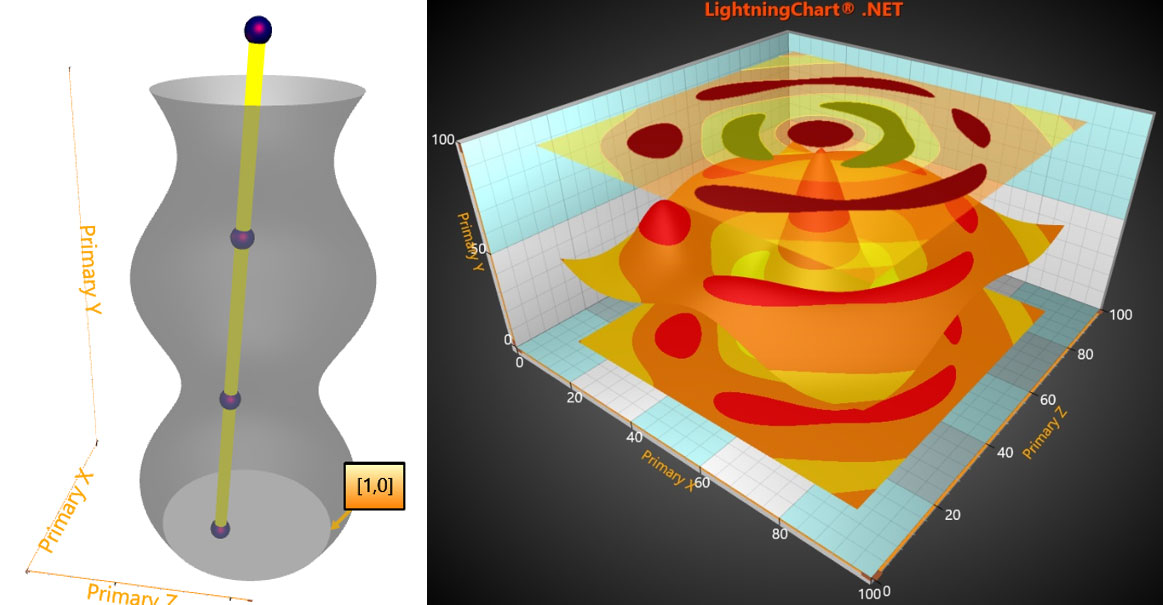
数据可视化工具LightningChart .NET正式发布v10.5.1——拥有全新的3D新功能
LightningChart.NET完全由GPU加速,并且性能经过优化,可用于实时显示海量数据-超过10亿个数据点。 LightningChart包括广泛的2D,高级3D,Polar,Smith,3D饼/甜甜圈,地理地图和GIS图表以及适用于科学…...

AWS认证SAA-C03每日一题
本题库由云计算狂魔微信公众号分享。 【SAA-C03助理级解决方案架构师认证】A company has a multi-tier application that runs six front-end web servers in an Amazon EC2 Auto Scaling group in a single Availability Zone behind an Application Load Balancer(ALB).A …...
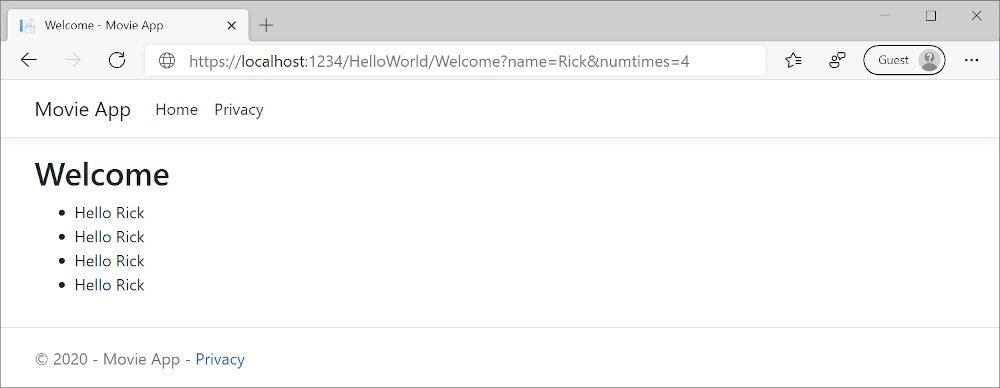
ASP.NET Core MVC -- 将视图添加到 ASP.NET Core MVC 应用
Index页 右键单击“视图”文件夹,然后单击“添加”>>“新文件夹”,并将文件夹命名为“HelloWorld”。 右键单击“Views/HelloWorld”文件夹,然后单击“添加”>“新项”。 在“添加新项 - MvcMovie”对话框中: 在右上…...
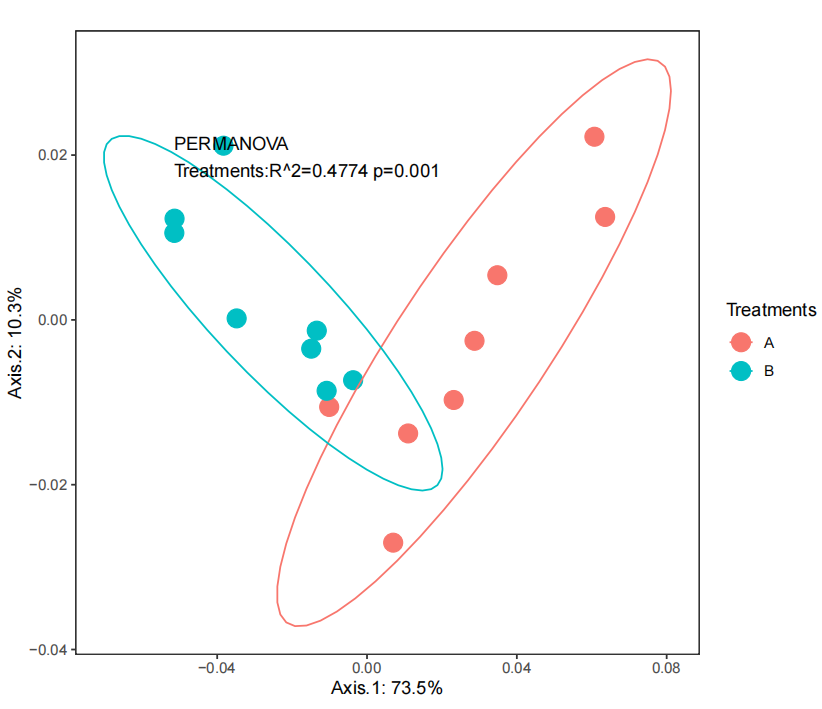
基于R做宏基因组结果的PCoA分析
写在前面 因为公司给的PCA结果效果不佳,决定从中重新挑选部分样本进行再分析 步骤 表格结果预处理 在属水平genus参考原本结果已有的PCA图,尽可能挑选距离较远且聚团的样本 选取不同样本属水平的丰度数据,整理成逗号分隔的csv文件 代码…...

8.10 算法刷题【1道题】
8.10 算法刷题 22. 链表中环的入口结点(快慢指针) 22. 链表中环的入口结点(快慢指针) 原题链接 /*** Definition for singly-linked list.* struct ListNode {* int val;* ListNode *next;* ListNode(int x) : val(x…...
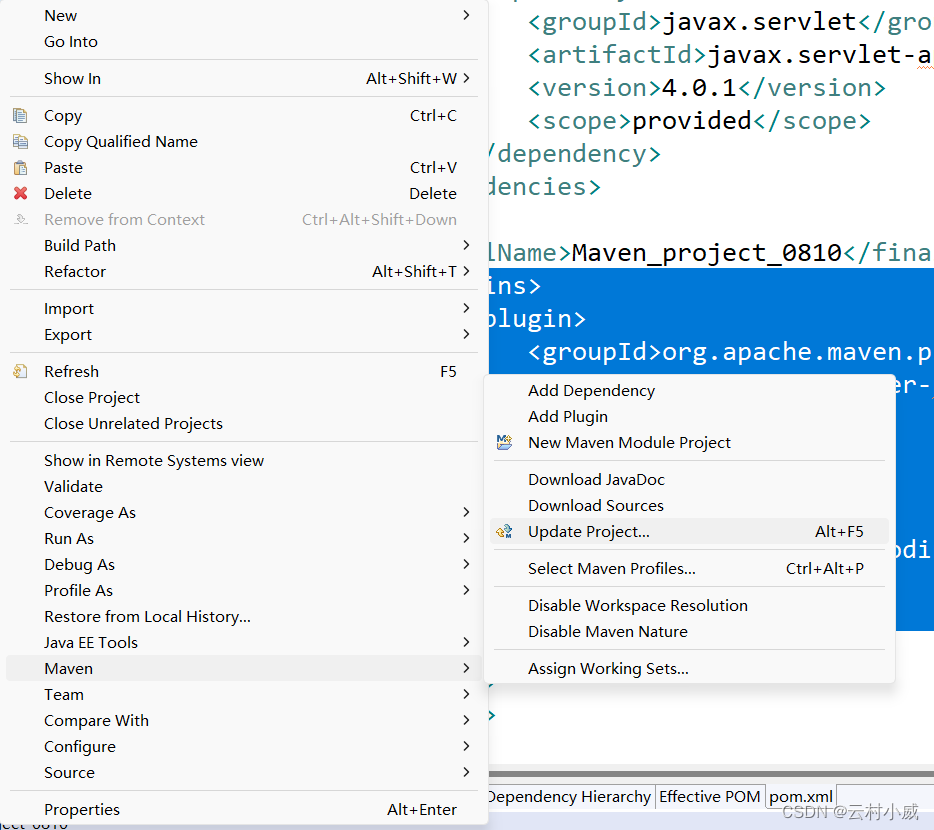
Apache Maven:从构建到部署,一站式解决方案
目录 一、Maven介绍 1. Maven是什么? 2.Maven的作用? 二、Maven仓库介绍 2.1 库的分类 三、Maven安装与配置 3.1 Maven安装 3.2 Maven环境配置 3.3 仓库配置 四、Eclipse与Maven配置 五、Maven项目测试 5.1 新建Maven项目步骤及注意事项 5.…...

文章四:版本控制策略 - 穿越时光机:Git版本控制进阶技巧
开始本篇文章之前先推荐一个好用的学习工具,AIRIght,借助于AI助手工具,学习事半功倍。欢迎访问:http://airight.fun 概述 版本控制是Git的核心功能,它使得开发者可以记录代码的历史变更,并能够在不同版本…...
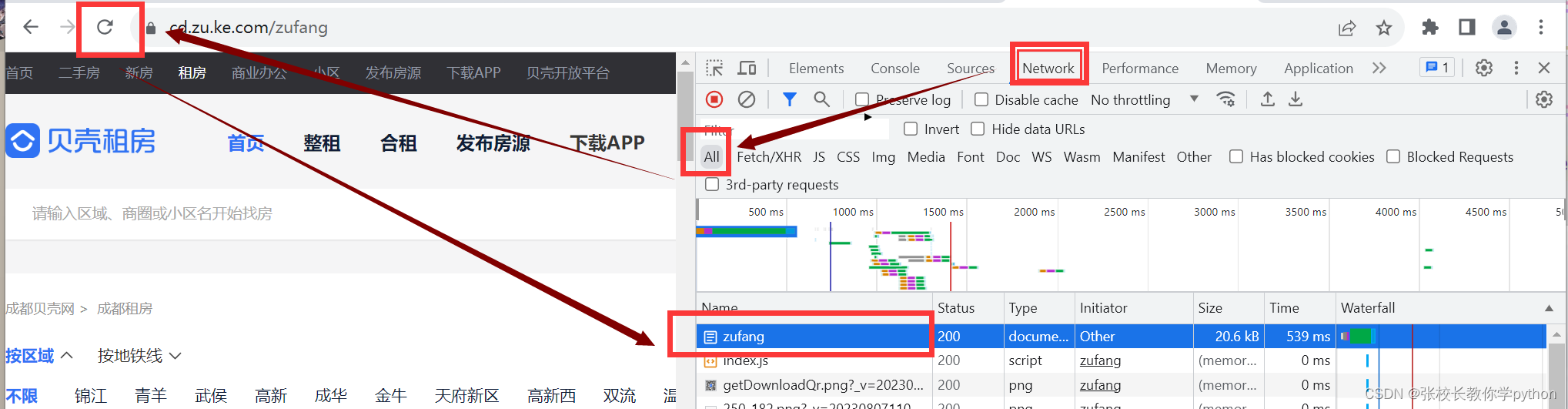
爬虫如何应对网站的反爬机制?如何查找user-agent对应的值
import requestsurl https://movie.douban.com/top250 response requests.get(url) # 查看结果 print(response)在requests使用一文中我们有讲到,当状态码不是200时表示爬虫不可用,也就是说我们获取不到网页源代码。但是我们还是可以挣扎一下ÿ…...
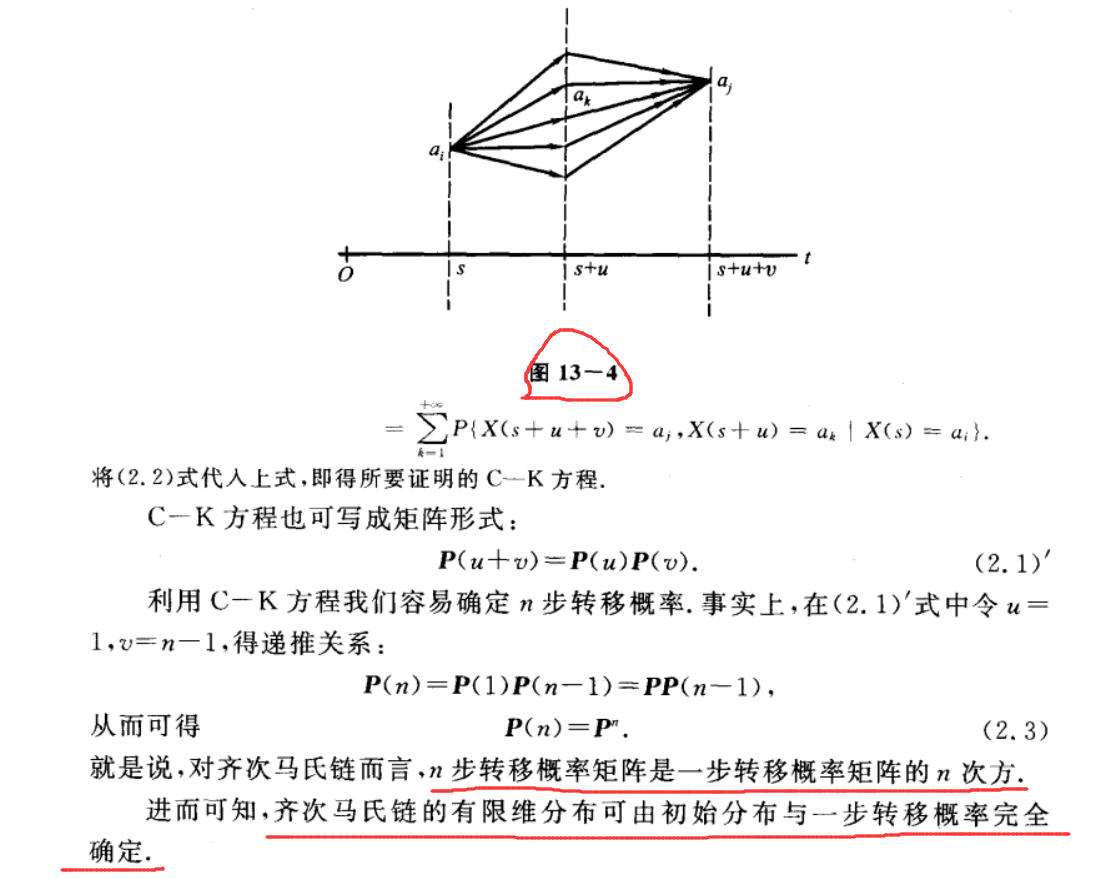
一个概率论例题引发的思考
浙江大学版《概率论与梳理统计》一书中的,第13章第1节例2如下: 这个解释和模型比较简单易懂。接下来,第2节的例2是一个关于此模型的题目: 在我自己的理解中,此题的解法跟上一个题目一样,第二级传输后&…...
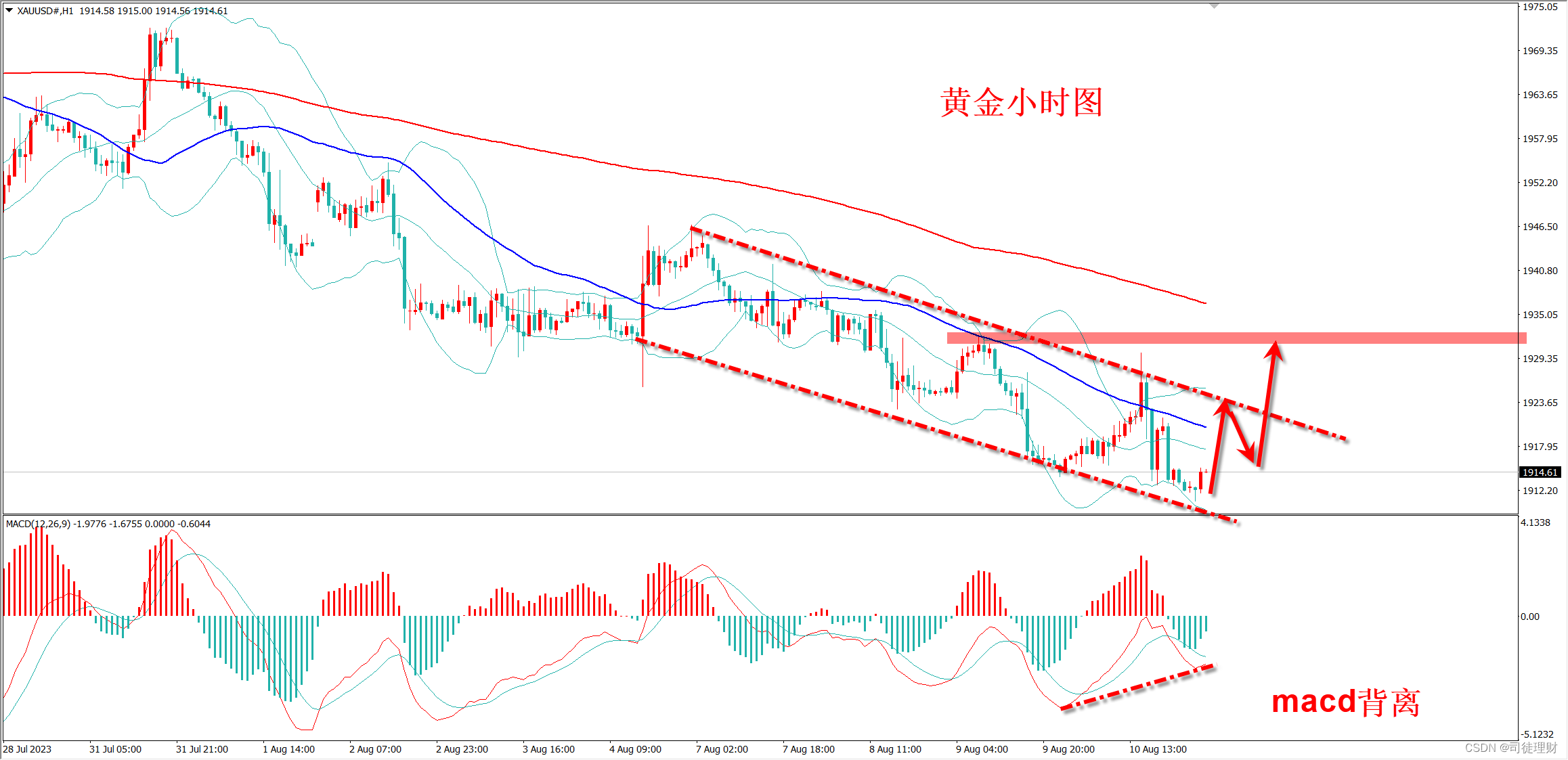
司徒理财:8.11黄金最新走势分析早盘1914现价多
黄金昨日再次破位新低,但是下跌力度出现衰竭迹象,意味着本次下跌暂时告一段落,行情将会开启一波反弹,早盘1914现价直接多,先看反弹上涨!黄金从走势上看,日线上已经跌至前低附近,也是…...

请写一个非对称加密工具 示例包括完整的通信流程
非对称加密工具通常用于保护数据的机密性和身份验证。下面是一个简化的示例,展示了完整的通信流程,包括密钥生成、加密、解密和数字签名验证: import java.security.KeyPair; import java.security.KeyPairGenerator; import java.security.…...
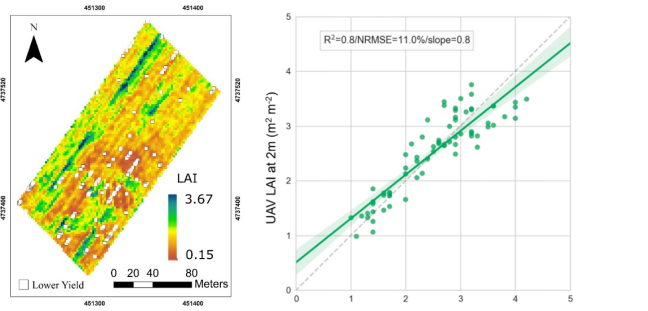
近地面无人机植被定量遥感与生理参数反演技术
遥感(RS-Remote Sensing)——不接触物体本身,用传感器收集目标物的电磁波信息,经处理、分析后,识别目标物,揭示其几何、物理性质和相互关系及其变化规律的现代科学技术。 换言之,即是“遥远的感…...

卡巴斯基为基于Linux的嵌入式设备推出专用解决方案
导读卡巴斯基在其卡巴斯基嵌入式系统安全产品中引入了对 Linux 的支持。这种适应性强的多层解决方案现在为基于Linux的嵌入式系统、设备和场景提供优化的安全,合通常适用于这些系统的严格监管标准。 卡巴斯基在其卡巴斯基嵌入式系统安全产品中引入了对 Linux 的支持…...

Word转PDF工具哪家安全?推荐好用的文件格式转换工具
Word文档是我们最常见也是最常用的办公软件,想必大家都知道了Word操作起来十分的简单,而且功能也是比较齐全的。随着科技的不断进步,如今也是有越来越多类型的办公文档,PDF就是其中之一,那么word转pdf怎么转?Word转PD…...

dma_mmap_coherent函数的使用
dma_mmap_coherent函数可以将dma地址映射到用户态,通过应用程序直接操作dma地址。 实现应该分配一段dma地址,例如: buf_addr dmam_alloc_coherent(&pdev->dev, size, &dma_addr, GFP_KERNEL);buf_addr 是内核态的虚拟地址&…...

MySQL_DQL语句(查询语句以及常用函数)
基础查询 不带条件的查询查询多个字段 语法: #查询指定字段的数据 SELECT 字段1, 字段2, 字段3 ... FROM 表名 ; #查询表中全部字段的数据 SELECT * FROM 表名 ;案例:查询表中所有信息数据 SELECT * FROM employee;案例:查询表中姓名和性别…...
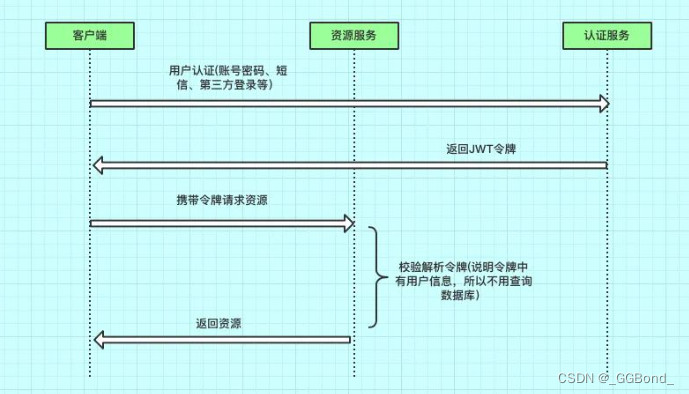
一步步教你实现JWT认证和授权
一步步教你实现JWT认证和授权 前言一、引入二、Token认证与JWT认证的关系三、什么是JWT认证?四、JWT的组成1、头部(Header)2、载荷(Payload)3、签名(Signature) 五、JWT认证的工作流程六、代码举…...

【python 深度学习】解决遇到的问题
目录 一、RuntimeError: module compiled against API version 0xc but this version of numpy is 0xb 二、AttributeError: module ‘tensorflow’ has no attribute ‘flags’ 三、conda 更新 Please update conda by running 四、to search for alternate channels that…...

【SpringBoot】100、SpringBoot中使用自定义注解+AOP实现参数自动解密
在实际项目中,用户注册、登录、修改密码等操作,都涉及到参数传输安全问题。所以我们需要在前端对账户、密码等敏感信息加密传输,在后端接收到数据后能自动解密。 1、引入依赖 <dependency><groupId>org.springframework.boot</groupId><artifactId...

条件运算符
C中的三目运算符(也称条件运算符,英文:ternary operator)是一种简洁的条件选择语句,语法如下: 条件表达式 ? 表达式1 : 表达式2• 如果“条件表达式”为true,则整个表达式的结果为“表达式1”…...

Linux-07 ubuntu 的 chrome 启动不了
文章目录 问题原因解决步骤一、卸载旧版chrome二、重新安装chorme三、启动不了,报错如下四、启动不了,解决如下 总结 问题原因 在应用中可以看到chrome,但是打不开(说明:原来的ubuntu系统出问题了,这个是备用的硬盘&a…...

深入解析C++中的extern关键字:跨文件共享变量与函数的终极指南
🚀 C extern 关键字深度解析:跨文件编程的终极指南 📅 更新时间:2025年6月5日 🏷️ 标签:C | extern关键字 | 多文件编程 | 链接与声明 | 现代C 文章目录 前言🔥一、extern 是什么?&…...

浅谈不同二分算法的查找情况
二分算法原理比较简单,但是实际的算法模板却有很多,这一切都源于二分查找问题中的复杂情况和二分算法的边界处理,以下是博主对一些二分算法查找的情况分析。 需要说明的是,以下二分算法都是基于有序序列为升序有序的情况…...

鸿蒙DevEco Studio HarmonyOS 5跑酷小游戏实现指南
1. 项目概述 本跑酷小游戏基于鸿蒙HarmonyOS 5开发,使用DevEco Studio作为开发工具,采用Java语言实现,包含角色控制、障碍物生成和分数计算系统。 2. 项目结构 /src/main/java/com/example/runner/├── MainAbilitySlice.java // 主界…...

Fabric V2.5 通用溯源系统——增加图片上传与下载功能
fabric-trace项目在发布一年后,部署量已突破1000次,为支持更多场景,现新增支持图片信息上链,本文对图片上传、下载功能代码进行梳理,包含智能合约、后端、前端部分。 一、智能合约修改 为了增加图片信息上链溯源,需要对底层数据结构进行修改,在此对智能合约中的农产品数…...

OCR MLLM Evaluation
为什么需要评测体系?——背景与矛盾 能干的事: 看清楚发票、身份证上的字(准确率>90%),速度飞快(眨眼间完成)。干不了的事: 碰到复杂表格(合并单元…...

Mysql故障排插与环境优化
前置知识点 最上层是一些客户端和连接服务,包含本 sock 通信和大多数jiyukehuduan/服务端工具实现的TCP/IP通信。主要完成一些简介处理、授权认证、及相关的安全方案等。在该层上引入了线程池的概念,为通过安全认证接入的客户端提供线程。同样在该层上可…...

用 FFmpeg 实现 RTMP 推流直播
RTMP(Real-Time Messaging Protocol) 是直播行业中常用的传输协议。 一般来说,直播服务商会给你: ✅ 一个 RTMP 推流地址(你推视频上去) ✅ 一个 HLS 或 FLV 拉流地址(观众观看用)…...
