一个概率论例题引发的思考
浙江大学版《概率论与梳理统计》一书中的,第13章第1节例2如下:

这个解释和模型比较简单易懂。接下来,第2节的例2是一个关于此模型的题目:

在我自己的理解中,此题的解法跟上一个题目一样,第二级传输后,一共有4中可能性,按照平均概率相加即可。
{ p n q n q n p n } \begin {Bmatrix} p^n & q^n \\ q^n & p^n \end{Bmatrix} {pnqnqnpn}
然而,仔细考虑之后发现不妥。因为最后结果的概率,这样计算不太合适,但是又没有发现更合理的理论和方法,又看到这一节的如下论述:


似乎抓到了什么,但是又特别模糊。
再看以下C-K方程:

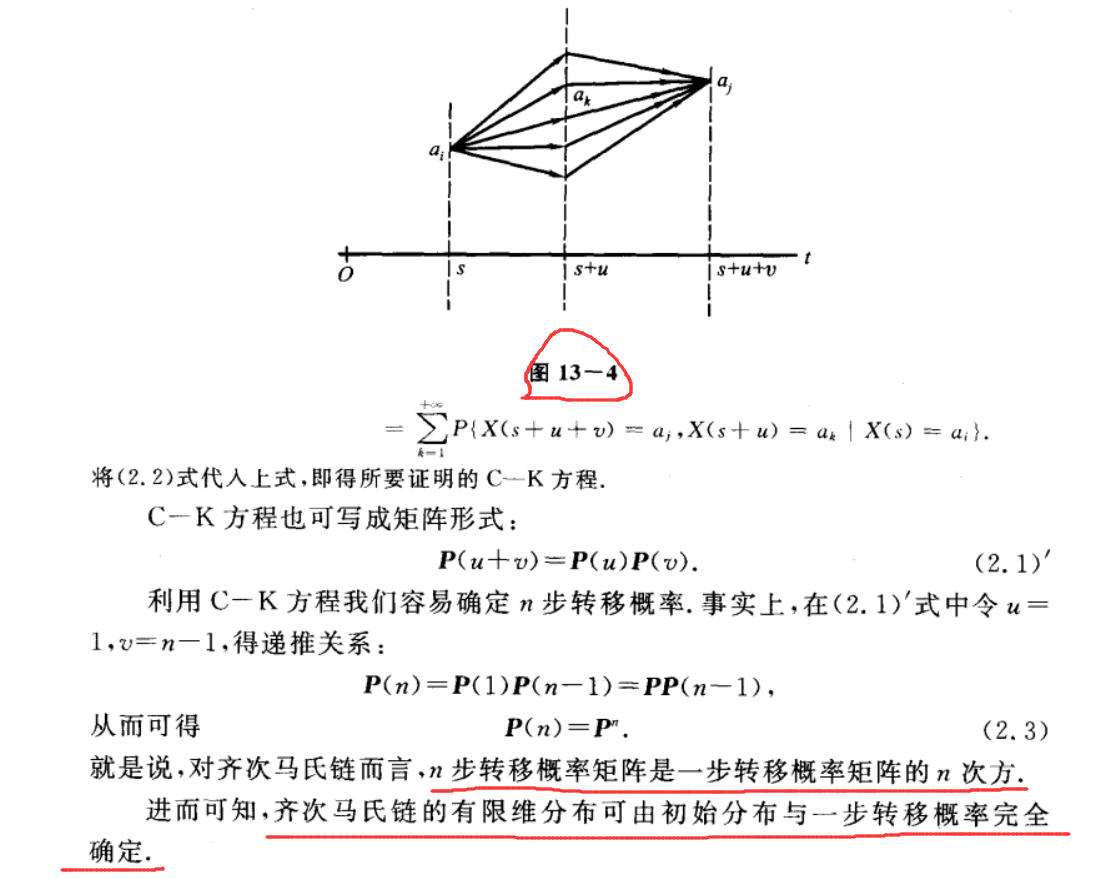
因此,参考此文:https://blog.csdn.net/m0_37567738/article/details/132182007?spm=1001.2014.3001.5502可以得出结论,此种题目的解题方法还是要回到马尔可夫概率转移矩阵中去找答案。
我觉得要理解此题目的底层逻辑,还需要了解以下公式:
P { X n = a n } = ∑ i = 1 + ∞ P { X n = a n , X 0 = a i } = ∑ i = 1 + ∞ P { X n = a n ∣ X 0 = a i } P { X 0 = a i } = ∑ i = 1 + ∞ P i ( 0 ) P i j ( n ) = ∑ i = 1 + ∞ P i 1 ( 1 ) P i j ( n − 1 ) = ∑ i = 1 + ∞ P 2 i ( 2 ) P i j ( n − 2 ) = ∑ i = 1 + ∞ P 3 i ( 3 ) P i j ( n − 3 ) = . . . . . . P \{X_n = a_n\} = \sum_{i = 1}^{+\infty} P\{ X_n = a_n, X_0 = a_i \} = \\ \sum_{i = 1}^{+\infty} P\{ X_n = a_n|X_0 = a_i \} P\{ X_0 = a_i \}=\sum_{i=1}^{+\infty} P_i(0) P_{ij}(n) = \\ \sum_{i=1}^{+\infty} P_{i1}(1) P_{ij}(n-1)= \sum_{i=1}^{+\infty} P_{2i}(2) P_{ij}(n-2) = \sum_{i=1}^{+\infty} P_{3i}(3) P_{ij}(n-3) = ...... \\ P{Xn=an}=i=1∑+∞P{Xn=an,X0=ai}=i=1∑+∞P{Xn=an∣X0=ai}P{X0=ai}=i=1∑+∞Pi(0)Pij(n)=i=1∑+∞Pi1(1)Pij(n−1)=i=1∑+∞P2i(2)Pij(n−2)=i=1∑+∞P3i(3)Pij(n−3)=......
这个逻辑的本质区别就在于,它是利用后验概率去推算先验概率的,这是一种理论上的优越性。
我们想要求解的概率P,它依赖于其概率矩阵的乘法运算,而不是说简单把4种转换相加。
相关文章:

一个概率论例题引发的思考
浙江大学版《概率论与梳理统计》一书中的,第13章第1节例2如下: 这个解释和模型比较简单易懂。接下来,第2节的例2是一个关于此模型的题目: 在我自己的理解中,此题的解法跟上一个题目一样,第二级传输后&…...
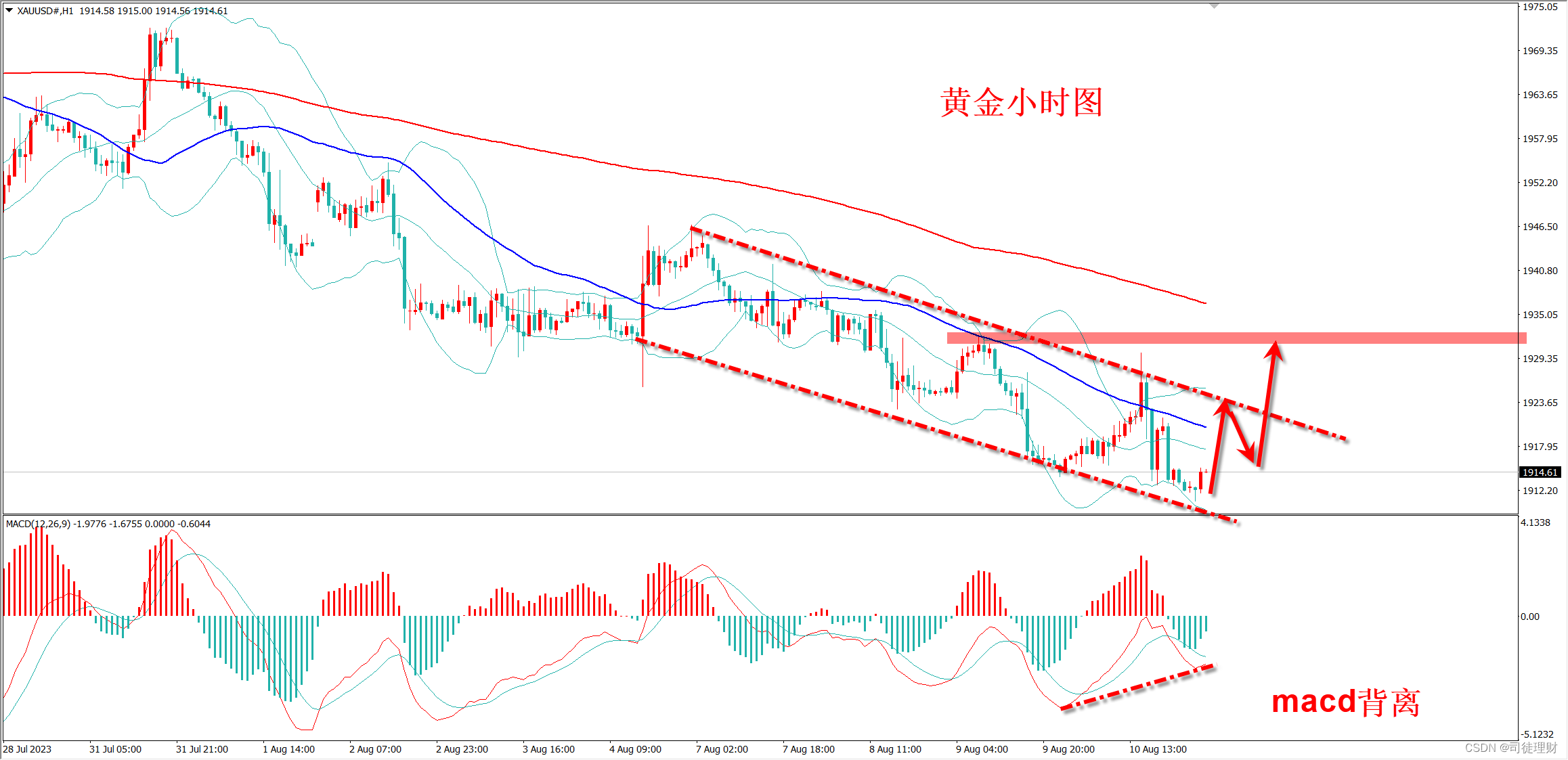
司徒理财:8.11黄金最新走势分析早盘1914现价多
黄金昨日再次破位新低,但是下跌力度出现衰竭迹象,意味着本次下跌暂时告一段落,行情将会开启一波反弹,早盘1914现价直接多,先看反弹上涨!黄金从走势上看,日线上已经跌至前低附近,也是…...

请写一个非对称加密工具 示例包括完整的通信流程
非对称加密工具通常用于保护数据的机密性和身份验证。下面是一个简化的示例,展示了完整的通信流程,包括密钥生成、加密、解密和数字签名验证: import java.security.KeyPair; import java.security.KeyPairGenerator; import java.security.…...
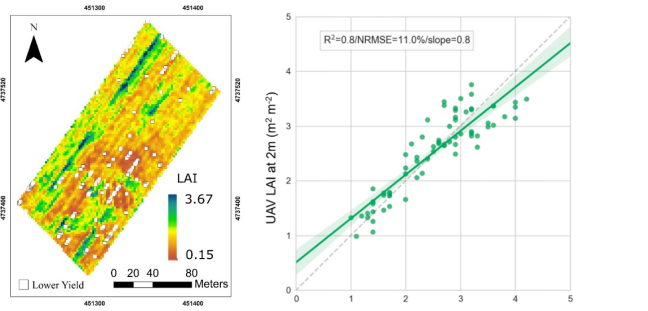
近地面无人机植被定量遥感与生理参数反演技术
遥感(RS-Remote Sensing)——不接触物体本身,用传感器收集目标物的电磁波信息,经处理、分析后,识别目标物,揭示其几何、物理性质和相互关系及其变化规律的现代科学技术。 换言之,即是“遥远的感…...

卡巴斯基为基于Linux的嵌入式设备推出专用解决方案
导读卡巴斯基在其卡巴斯基嵌入式系统安全产品中引入了对 Linux 的支持。这种适应性强的多层解决方案现在为基于Linux的嵌入式系统、设备和场景提供优化的安全,合通常适用于这些系统的严格监管标准。 卡巴斯基在其卡巴斯基嵌入式系统安全产品中引入了对 Linux 的支持…...

Word转PDF工具哪家安全?推荐好用的文件格式转换工具
Word文档是我们最常见也是最常用的办公软件,想必大家都知道了Word操作起来十分的简单,而且功能也是比较齐全的。随着科技的不断进步,如今也是有越来越多类型的办公文档,PDF就是其中之一,那么word转pdf怎么转?Word转PD…...

dma_mmap_coherent函数的使用
dma_mmap_coherent函数可以将dma地址映射到用户态,通过应用程序直接操作dma地址。 实现应该分配一段dma地址,例如: buf_addr dmam_alloc_coherent(&pdev->dev, size, &dma_addr, GFP_KERNEL);buf_addr 是内核态的虚拟地址&…...

MySQL_DQL语句(查询语句以及常用函数)
基础查询 不带条件的查询查询多个字段 语法: #查询指定字段的数据 SELECT 字段1, 字段2, 字段3 ... FROM 表名 ; #查询表中全部字段的数据 SELECT * FROM 表名 ;案例:查询表中所有信息数据 SELECT * FROM employee;案例:查询表中姓名和性别…...
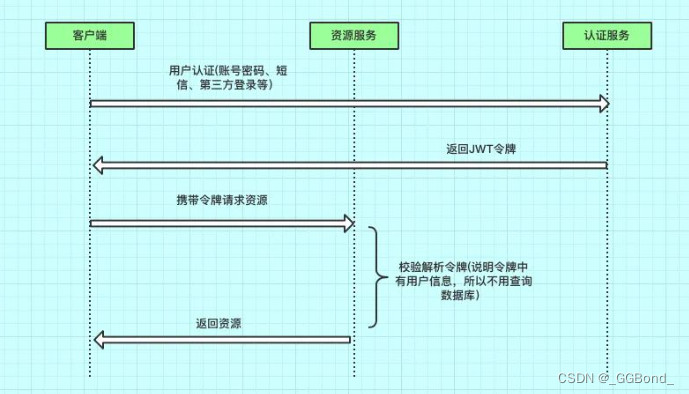
一步步教你实现JWT认证和授权
一步步教你实现JWT认证和授权 前言一、引入二、Token认证与JWT认证的关系三、什么是JWT认证?四、JWT的组成1、头部(Header)2、载荷(Payload)3、签名(Signature) 五、JWT认证的工作流程六、代码举…...

【python 深度学习】解决遇到的问题
目录 一、RuntimeError: module compiled against API version 0xc but this version of numpy is 0xb 二、AttributeError: module ‘tensorflow’ has no attribute ‘flags’ 三、conda 更新 Please update conda by running 四、to search for alternate channels that…...

maxwell 基于zookeeper的高可用方案
Maxwell版本1.39.2 一: 添加zk的pox文件 <!-- customize HA --> <dependency><groupId>org.apache.curator</groupId><artifactId>curator-framework</artifactId><version>5.4.0</version> </dependency>&…...
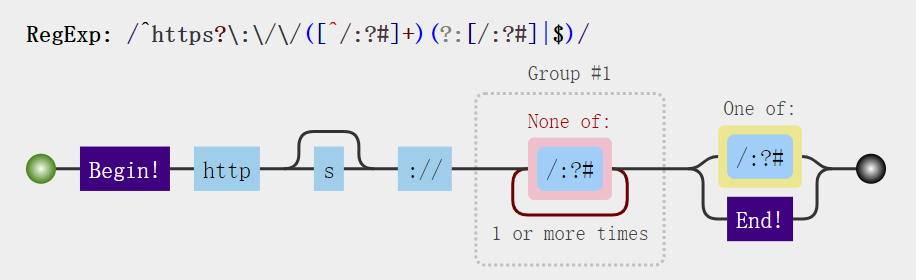
【JavaScript】match用法 | 正则匹配
match正则匹配 var e "www.apple.com:baidu.com" var match e.match(/com/g) console.log("match: "match);> "match: com,com"match返回值问题 match的返回值是一个数组 数组的第0个元素是与整个正则表达式匹配的结果 数组的第1个元素是…...

前端css + js +vue +element-ui 实现响应式布局,根据浏览器窗体大小自动响应
前端css js vue element-ui 实现响应式布局,根据浏览器窗体大小自动响应 1、环境2、js代码3、代码解释1、定义对象2、定义方法3、监听窗口变化,计算比例值,并赋值给transform 属性4、实现监听 3、html 代码4、特别注意 1、环境 我的环境是e…...
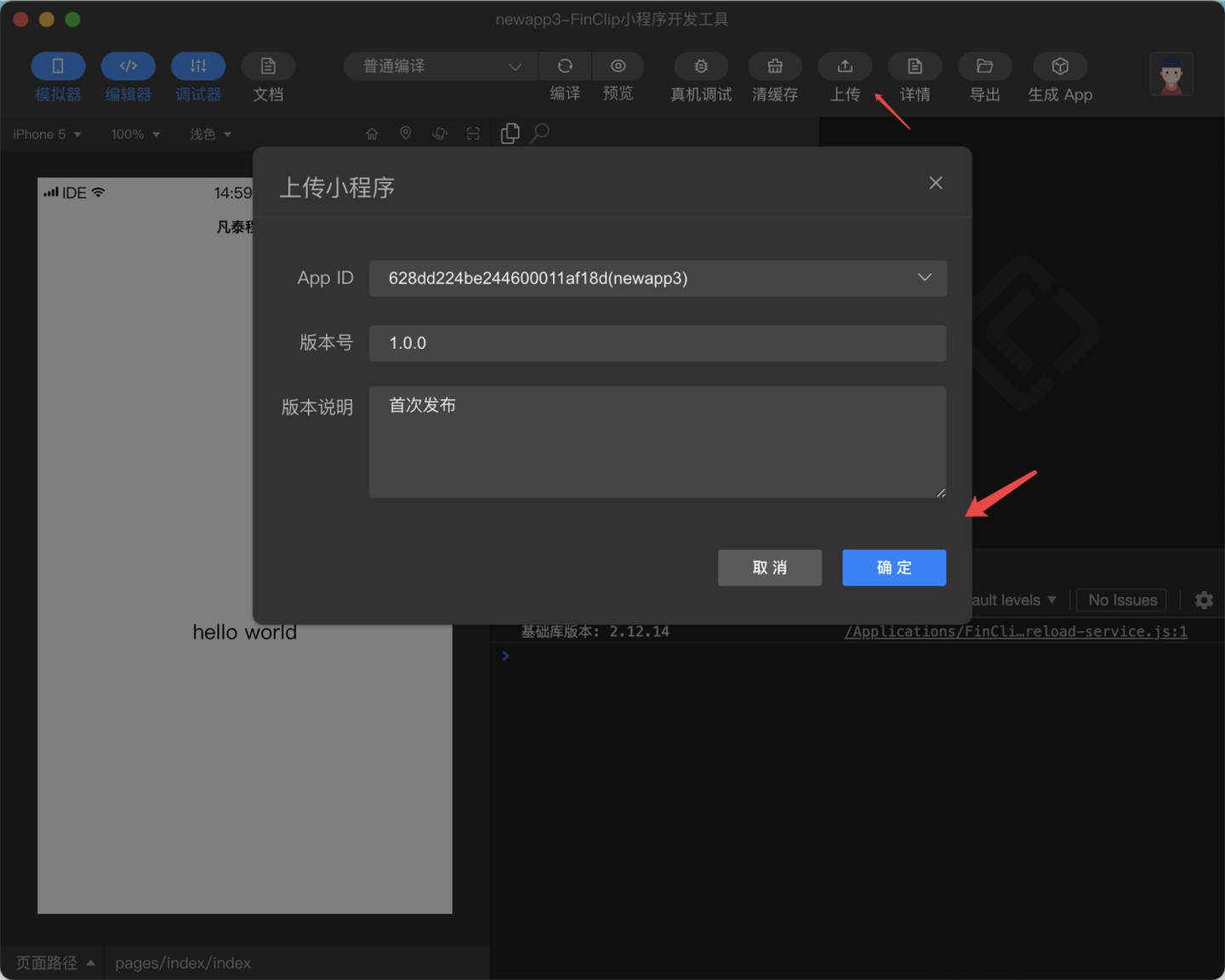
小程序生成App:轻量低门槛的开发方式
小程序生成App可以成为一种轻量低门槛的开发App的方式,但是需要根据具体情况进行选择。如果应用需要处理大量数据或需要进行复杂计算,或者需要实现原生特有的功能或交互效果,可能需要选择其他开发方式。 在文章开始之前,我们看看目…...
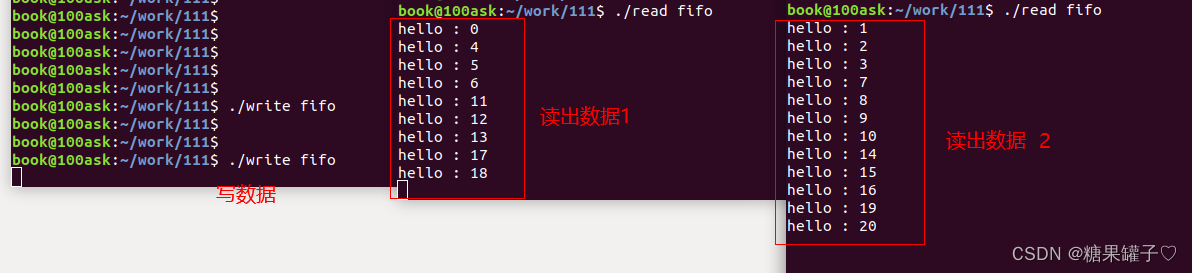
Linux命名管道进程通信
文章目录 前言一、什么是命名管道通信二、创建方式三、代码示例四、文件进程通信总结 前言 命名管道 是实现进程间通信的强大工具,它提供了一种简单而有效的方式,允许不同进程之间进行可靠的数据交换。不仅可以在同一主机上的不相关进程间进行通信&…...
如何将苹果彻底删除视频找回?试试这3种方法
如今是短视频时代,大家通常会使用苹果手机来拍摄视频,以此记录生活中的美好日常。但是大家都知道视频是十分占空间的,这也经常会出现iPhone内存不足,磁盘崩溃的问题。 当遇到iPhone内存不足的情况时,大家往往会选择清…...
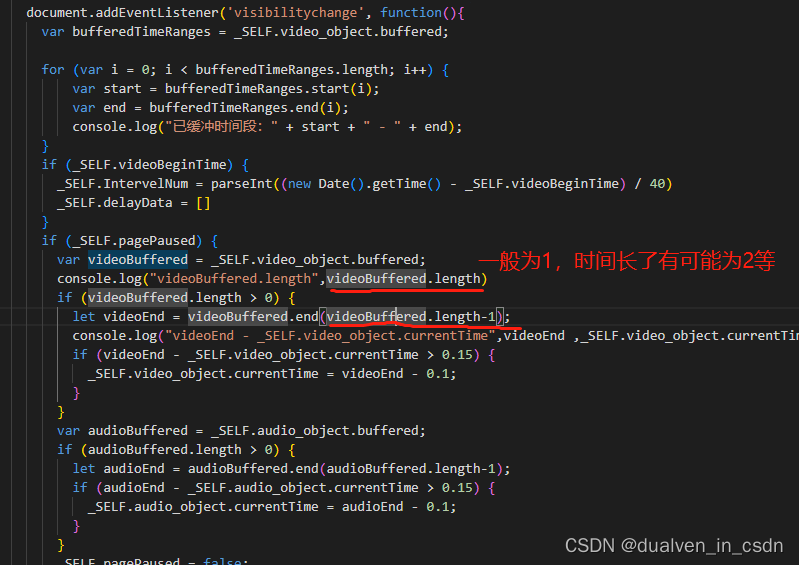
【音视频、chatGpt】h5页面最小化后,再激活后视频停住问题的解决
目录 现象 观察 解决 现象 页面有时候要切换,要最小化;短时间或者几个小时内切换回来,视频可以正常续上;而放置较长时间,几个小时或者一晚上,切换回来后,视频可能卡死 观察 切换页面&#x…...

[CSS] 图片九宫格
效果 index.html <!DOCTYPE html> <html lang"en"><head><meta charset"UTF-8"/><meta http-equiv"X-UA-Compatible" content"IEedge"/><meta name"viewport" content"widthdevice-…...
MChat-Gpt V1.0.0 (将ChatGpt机器人接入内网供全体使用)
Github>https://github.com/MartinxMax/MChat-Gpt 首页 MChat-Gpt V1.0.0将ChatGpt机器人接入内网供全体使用 你需要一个ChatGpt账户如果您在中国则需要使用代理访问,设置TUN代理模式 安装依赖 选择你的系统进行安装 服务端配置 #python3 ChatGpt_Server.py -h 使用&a…...
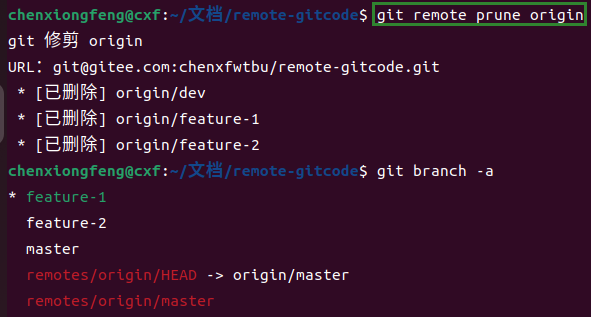
日常开发中Git命令指北
Git基本操作 创建化仓库 mkdir 目录 cd 目录 git init配置本地仓库 # 配置用户名,邮箱 git config user.name "cxf" git config user.email "1969612859qq.com" # 查看本地配置(小写的 L) git config -l # 重置配置&a…...

HTML 列表、表格、表单
1 列表标签 作用:布局内容排列整齐的区域 列表分类:无序列表、有序列表、定义列表。 例如: 1.1 无序列表 标签:ul 嵌套 li,ul是无序列表,li是列表条目。 注意事项: ul 标签里面只能包裹 li…...

屋顶变身“发电站” ,中天合创屋面分布式光伏发电项目顺利并网!
5月28日,中天合创屋面分布式光伏发电项目顺利并网发电,该项目位于内蒙古自治区鄂尔多斯市乌审旗,项目利用中天合创聚乙烯、聚丙烯仓库屋面作为场地建设光伏电站,总装机容量为9.96MWp。 项目投运后,每年可节约标煤3670…...
详解:相对定位 绝对定位 固定定位)
css的定位(position)详解:相对定位 绝对定位 固定定位
在 CSS 中,元素的定位通过 position 属性控制,共有 5 种定位模式:static(静态定位)、relative(相对定位)、absolute(绝对定位)、fixed(固定定位)和…...

ElasticSearch搜索引擎之倒排索引及其底层算法
文章目录 一、搜索引擎1、什么是搜索引擎?2、搜索引擎的分类3、常用的搜索引擎4、搜索引擎的特点二、倒排索引1、简介2、为什么倒排索引不用B+树1.创建时间长,文件大。2.其次,树深,IO次数可怕。3.索引可能会失效。4.精准度差。三. 倒排索引四、算法1、Term Index的算法2、 …...
的原因分类及对应排查方案)
JVM暂停(Stop-The-World,STW)的原因分类及对应排查方案
JVM暂停(Stop-The-World,STW)的完整原因分类及对应排查方案,结合JVM运行机制和常见故障场景整理而成: 一、GC相关暂停 1. 安全点(Safepoint)阻塞 现象:JVM暂停但无GC日志,日志显示No GCs detected。原因:JVM等待所有线程进入安全点(如…...

均衡后的SNRSINR
本文主要摘自参考文献中的前两篇,相关文献中经常会出现MIMO检测后的SINR不过一直没有找到相关数学推到过程,其中文献[1]中给出了相关原理在此仅做记录。 1. 系统模型 复信道模型 n t n_t nt 根发送天线, n r n_r nr 根接收天线的 MIMO 系…...

Xen Server服务器释放磁盘空间
disk.sh #!/bin/bashcd /run/sr-mount/e54f0646-ae11-0457-b64f-eba4673b824c # 全部虚拟机物理磁盘文件存储 a$(ls -l | awk {print $NF} | cut -d. -f1) # 使用中的虚拟机物理磁盘文件 b$(xe vm-disk-list --multiple | grep uuid | awk {print $NF})printf "%s\n"…...

VM虚拟机网络配置(ubuntu24桥接模式):配置静态IP
编辑-虚拟网络编辑器-更改设置 选择桥接模式,然后找到相应的网卡(可以查看自己本机的网络连接) windows连接的网络点击查看属性 编辑虚拟机设置更改网络配置,选择刚才配置的桥接模式 静态ip设置: 我用的ubuntu24桌…...

人工智能 - 在Dify、Coze、n8n、FastGPT和RAGFlow之间做出技术选型
在Dify、Coze、n8n、FastGPT和RAGFlow之间做出技术选型。这些平台各有侧重,适用场景差异显著。下面我将从核心功能定位、典型应用场景、真实体验痛点、选型决策关键点进行拆解,并提供具体场景下的推荐方案。 一、核心功能定位速览 平台核心定位技术栈亮…...

【免费数据】2005-2019年我国272个地级市的旅游竞争力多指标数据(33个指标)
旅游业是一个城市的重要产业构成。旅游竞争力是一个城市竞争力的重要构成部分。一个城市的旅游竞争力反映了其在旅游市场竞争中的比较优势。 今日我们分享的是2005-2019年我国272个地级市的旅游竞争力多指标数据!该数据集源自2025年4月发表于《地理学报》的论文成果…...
