回归决策树模拟sin函数
# -*-coding:utf-8-*-
import numpy as np
from sklearn import tree
import matplotlib.pyplot as pltplt.switch_backend("TkAgg")
# 创建了一个随机数生成器对象 rng
rng=np.random.RandomState(1)
print("rng",rng)
#5*rng.rand(80,1)生成一个80行、1列的数组,数组中的每个元素都是从0到5之间的随机数。然后,np.sort函数对这个数组进行排序,axis=0表示按行(也就是每一列)排序。
#axis=0,数组只有行,没有列
X=np.sort(5*rng.rand(80,1),axis=0)#ravel()把二维数组变为一位数组
y=np.sin(X).ravel()#选取0,5,10,15,20....,让这些下标数字加上噪声
y[::5]+=3*(0.5-rng.rand(16))regr_1=tree.DecisionTreeRegressor(max_depth=2)
regr_2=tree.DecisionTreeRegressor(max_depth=5)
clf1=regr_1.fit(X,y)
clf2=regr_2.fit(X,y)#转为二维数组
X_test=np.reshape( np.arange(0.0,5.0,0.01),(-1,1) )
# X_test=np.arrange(0.0,5.0,0.01)[:,np.newaxis]y_1=regr_1.predict(X_test)
y_2=regr_2.predict(X_test)plt.figure()
plt.scatter(X,y,s=20,edgecolors="black",c="darkorange",label="data")
plt.plot(X_test,y_1,color="cornflowerblue",label="max_depth=2",linewidth=2)
plt.plot(X_test,y_2,color="yellowgreen",label="max_depth=5",linewidth=2)
plt.xlabel("data")
plt.ylabel("target")
plt.title("Decision Tree Regreesion")
plt.legend()
plt.show()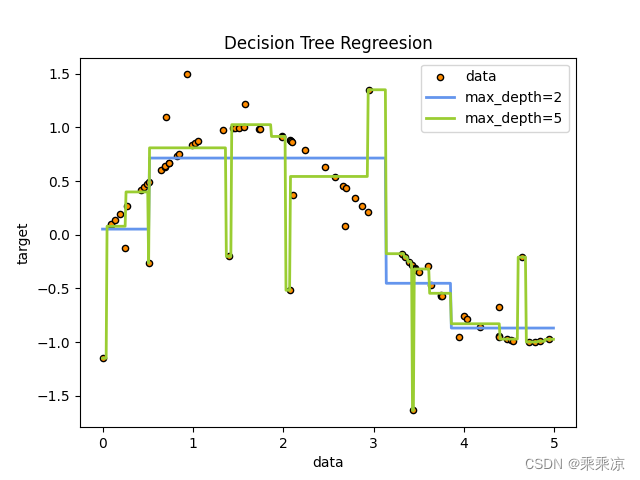
相关文章:

回归决策树模拟sin函数
# -*-coding:utf-8-*- import numpy as np from sklearn import tree import matplotlib.pyplot as pltplt.switch_backend("TkAgg") # 创建了一个随机数生成器对象 rng rngnp.random.RandomState(1) print("rng",rng) #5*rng.rand(80,1)生成一个80行、1列…...

NeRF基础代码解析
embedders 对position和view direction做embedding。 class FreqEmbedder(nn.Module):def __init__(self, in_dim3, multi_res10, use_log_bandsTrue, include_inputTrue):super().__init__()self.in_dim in_dimself.num_freqs multi_resself.max_freq_log2 multi_resself…...
职场新星:Java面试干货让你笑傲求职路(三)
职场新星:Java面试干货让你笑傲求职路 1、token 为什么存放在 redis 中?2、索引的底层原理是什么?3、Spring IOC和AOP的原理4、接口和抽象类有什么共同点和区别?5、为什么要使用线程池?直接new个线程不好吗?…...

获取指定收获地址的信息
目录 1 /// 获取指定收获地址的信息 2 /// 删除指定的收获地址信息 3 /// 取消订单 4 /// 确认订单收货 /// <summary> /// 获取指定收获地址的信息</...
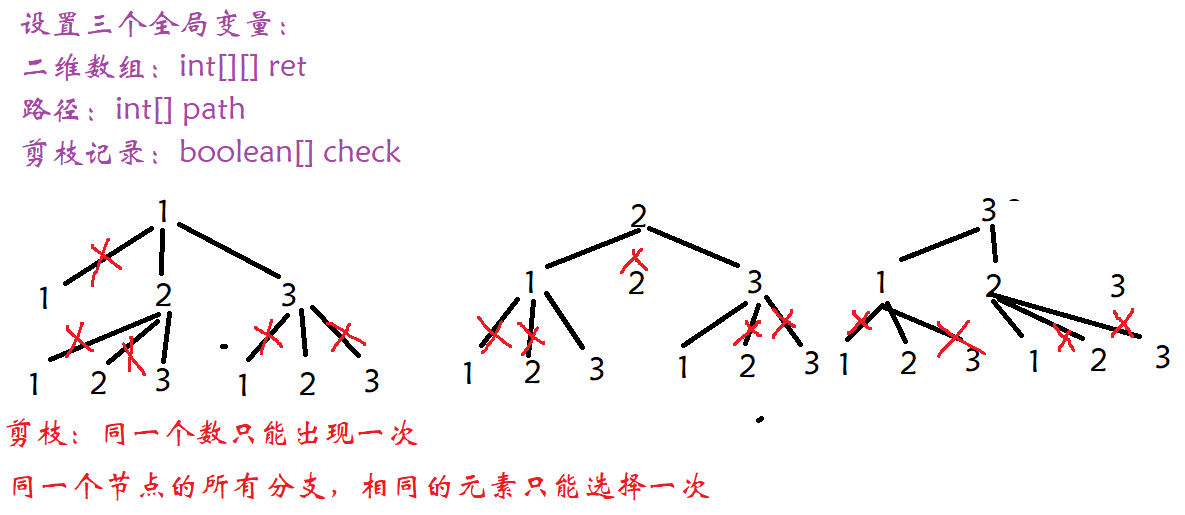
突破笔试:力扣全排列(medium)
1. 题目链接:46. 全排列 2. 题目描述:给定一个不含重复数字的数组 nums ,返回其 所有可能的全排列 。你可以 按任意顺序 返回答案。 示例 1: 输入:nums [1,2,3] 输出:[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[…...
gitlab 503 错误的解决方案
首先使用 sudo gitlab-ctl status 命令查看哪些服务没用启动 sudo gitlab-ctl status 再用 gitlab-rake gitlab:check 命令检查 gitlab。根据发生的错误一步一步纠正。 gitlab-rake gitlab:check 查看日志 tail /var/log/gitlab/gitaly/current删除gitaly.pid rm /var/opt…...

智能离子风棒联网监控静电消除器的主要功能和特点
智能离子风棒联网监控静电消除器是一种集成了智能化和网络化监控功能的设备,用于监测和消除静电现象。它的工作原理是通过产生大量的正负离子,将空气中的静电中和和消除,从而达到防止静电积累和放电的目的。 智能离子风棒联网监控静电消除器的…...
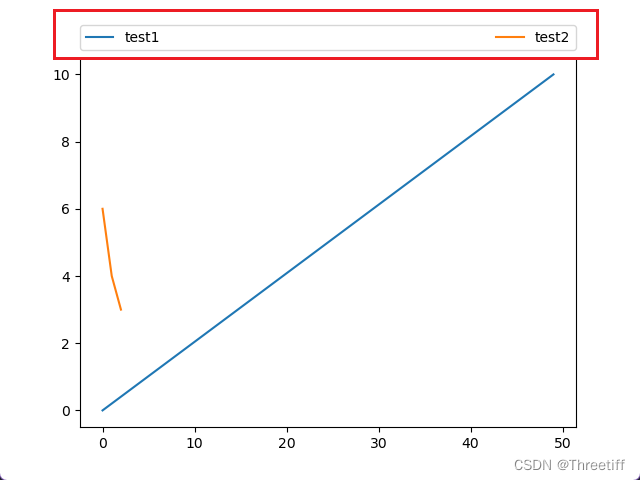
matplotlib 设置legend的位置在轴最上方,长度与图的长度相同
import matplotlib.pyplot as plt import numpy as npx1 np.linspace(0, 10, 50) x2 [6,4,3]ax plt.subplot() ax.plot(x1, label"test1") ax.plot(x2, label"test2") # 设置图例的位置 # 将左下角放置在【0, 1.02】位置处,横为1,…...

Docker-Compose 安装rabbitmq
【编写:docker-compose-rabbitmq.yml】创建数据目录: mkdir -p /opt/rabbitmq/data cd /opt/rabbitmq# 创建 docker-compose-rabbitmq.yml vim docker-compose-rabbitmq.yml 输入: version: "3.1" services:rabbitmq:image: rabbit…...

leetcode357- 2812. 找出最安全路径
这个题比较经典,可以用多个算法来求解,分别给出各个算法的求解方法,主要是分为第一部分的多源BFS求每个位置的距离和第二部分求(0,0)到(n-1,n-1)的最短路径(可以用多种方法求) 目录 多源BFS求最短路径枚举安全系数判断…...
Oracle连接数据库提示 ORA-12638:身份证明检索失败
ORA-12638 是一个 Oracle 数据库的错误代码,它表示身份验证(认证)检索失败。这通常与数据库连接相关,可能由于以下几个原因之一引起: 错误的用户名或密码: 提供的数据库用户名或密码不正确,导致…...

在 Linux 中使用 systemd 注册服务
Systemd 是一种现代的 Linux 系统初始化系统和服务管理器。它旨在管理系统服务的初始化、配置和控制。Systemd 的一个关键特性是它可以管理服务,这些服务是为系统提供特定功能的后台进程。在本指南中,我们将探讨如何使用 systemd 在 Linux 中注册服务。 …...

(03)Unity HTC VRTK 基于 URP 开发记录
1.简介 本篇主要内容为:URP如何与VRTK结合、URP需要注意的地方、VRTK的功能进行阐述。 因项目本身要求要渲染出比较好的画质,所以抛弃了Unity默认渲染管线Built-in,使用URP进行渲染,当然也可以选HDRP,但考虑到后期项目…...
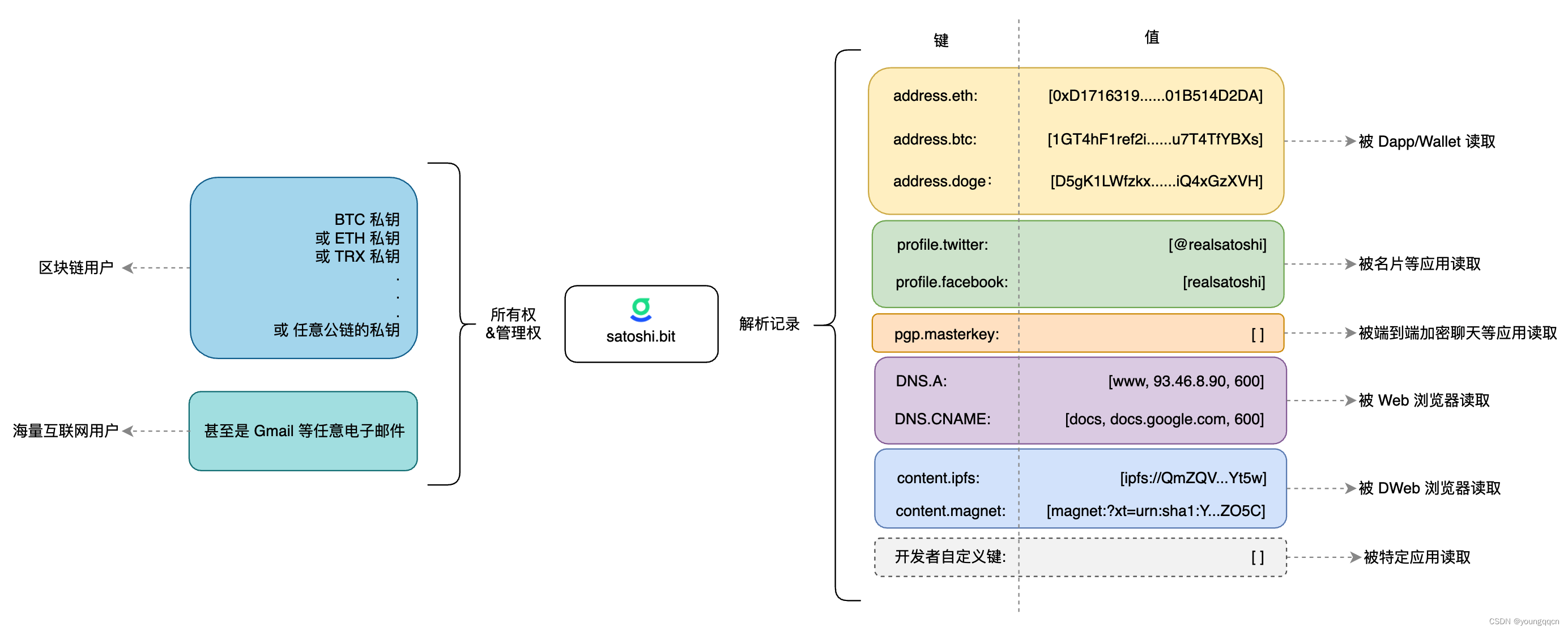
.bit域名调研
.bit域名研究 问题: .bit域名和ENS域名的相同点?不同点?有什么关系? .bit的定义 .bit 是基于区块链的,开源的,跨链去中心化账户系统.bit 提供了以 .bit 为后缀的全局唯一的命名体系,可用于加密…...
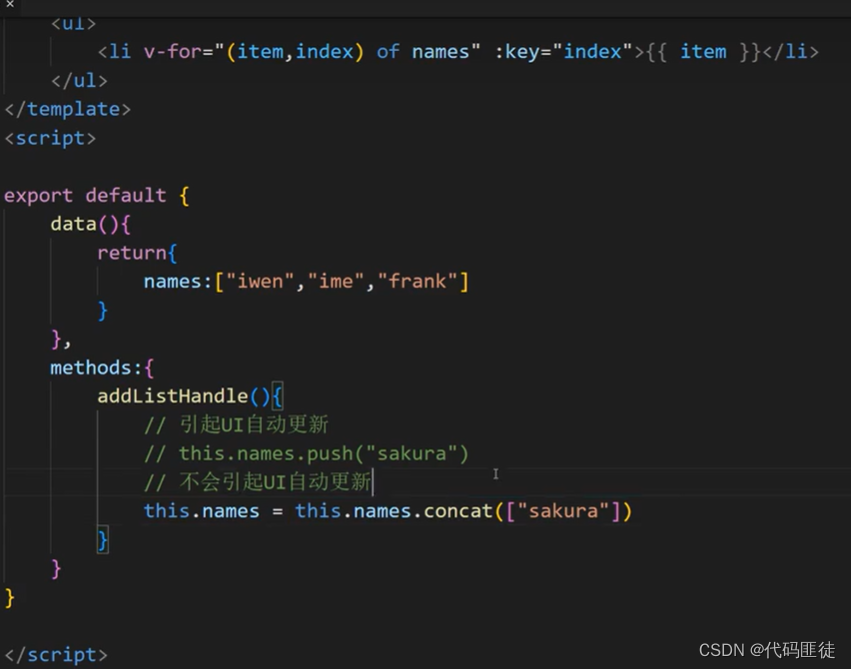
Vue数组变更方法和替换方法
一、可以引起UI界面变化 Vue 将被侦听的数组的变更方法进行了包裹,所以它们也将会触发视图更新。这些被包裹过的方法包括: push()pop()shift()unshift()splice()sort()reverse() 以上七个数组都会改变原数组,下面来分别讲解它们的区别&…...

Centos-6.3安装使用MongoDB
安装说明 系统环境:Centos-6.3 安装软件:mongodb-linux-x86_64-2.2.2.tgz 下载地址:http://www.mongodb.org/downloads 安装机器:192.168.15.237 上传位置:/usr/local/ 软件安装位置:/usr/local/mongodb 数…...

Mysql 复杂查询丨联表查询
💗wei_shuo的个人主页 💫wei_shuo的学习社区 🌐Hello World ! JOIN(联表查询) 联表查询(Join)是一种在数据库中使用多个表进行关联查询的操作。它通过使用 JOIN 关键字将多个表连接在…...
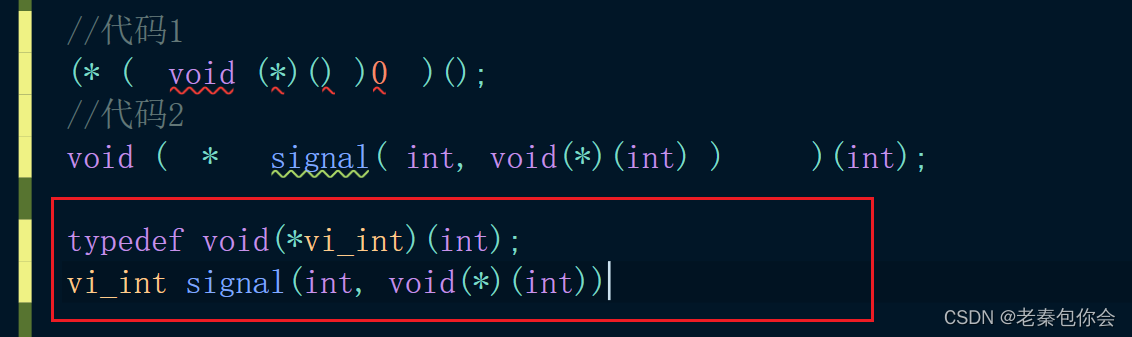
C语言进阶第二课-----------指针的进阶----------升级版
作者前言 🎂 ✨✨✨✨✨✨🍧🍧🍧🍧🍧🍧🍧🎂 🎂 作者介绍: 🎂🎂 🎂 🎉🎉🎉…...

若依vue -【 111 ~ 更 ~ 127 完 】
【更】111 3.5.0版本更新介绍 112 使用docker实现一键部署 1、安装docker yum install https://download.docker.com/linux/fedora/30/x86_64/stable/Packages/containerd.io-1.2.6-3.3.fc30.x86_64.rpm yum install -y yum-utils device-mapper-persistent-data lvm2 yum-c…...
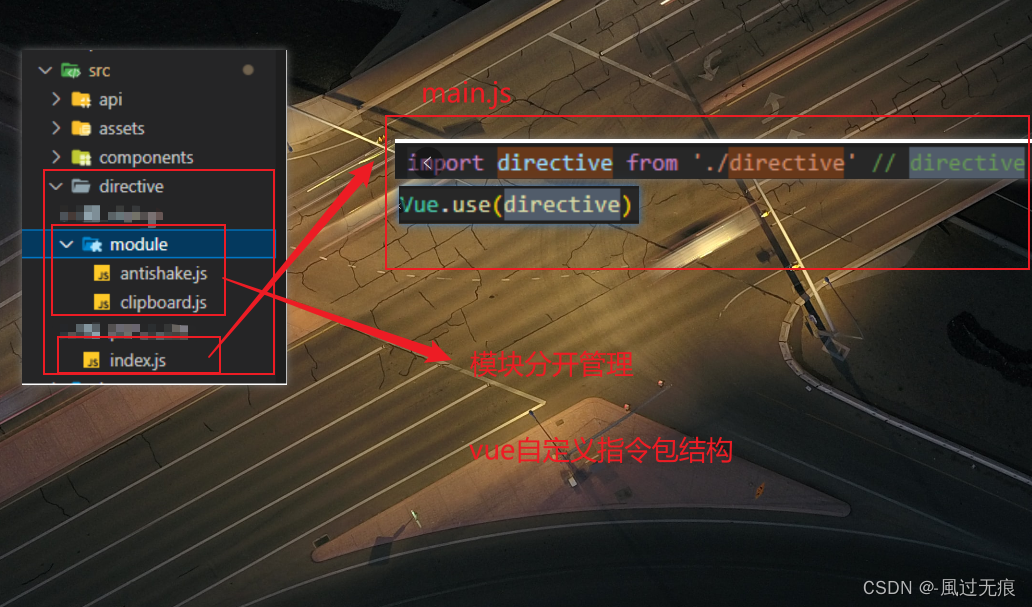
vue-pc端实现按钮防抖处理-自定义指令
前言 我们经常在移动端会处理按钮和输入框的防抖和节流处理,在pc端很少进行这样的操作 但是在pc端也是可以进行按钮的防抖操作,这样也是比较合理,可以不用但不可以不会 我们只要配合vue项目自定义指令加上全局注册,就可以实现按…...
详解)
后进先出(LIFO)详解
LIFO 是 Last In, First Out 的缩写,中文译为后进先出。这是一种数据结构的工作原则,类似于一摞盘子或一叠书本: 最后放进去的元素最先出来 -想象往筒状容器里放盘子: (1)你放进的最后一个盘子(…...

iOS 26 携众系统重磅更新,但“苹果智能”仍与国行无缘
美国西海岸的夏天,再次被苹果点燃。一年一度的全球开发者大会 WWDC25 如期而至,这不仅是开发者的盛宴,更是全球数亿苹果用户翘首以盼的科技春晚。今年,苹果依旧为我们带来了全家桶式的系统更新,包括 iOS 26、iPadOS 26…...

前端倒计时误差!
提示:记录工作中遇到的需求及解决办法 文章目录 前言一、误差从何而来?二、五大解决方案1. 动态校准法(基础版)2. Web Worker 计时3. 服务器时间同步4. Performance API 高精度计时5. 页面可见性API优化三、生产环境最佳实践四、终极解决方案架构前言 前几天听说公司某个项…...

EtherNet/IP转DeviceNet协议网关详解
一,设备主要功能 疆鸿智能JH-DVN-EIP本产品是自主研发的一款EtherNet/IP从站功能的通讯网关。该产品主要功能是连接DeviceNet总线和EtherNet/IP网络,本网关连接到EtherNet/IP总线中做为从站使用,连接到DeviceNet总线中做为从站使用。 在自动…...

多种风格导航菜单 HTML 实现(附源码)
下面我将为您展示 6 种不同风格的导航菜单实现,每种都包含完整 HTML、CSS 和 JavaScript 代码。 1. 简约水平导航栏 <!DOCTYPE html> <html lang"zh-CN"> <head><meta charset"UTF-8"><meta name"viewport&qu…...

Mysql中select查询语句的执行过程
目录 1、介绍 1.1、组件介绍 1.2、Sql执行顺序 2、执行流程 2.1. 连接与认证 2.2. 查询缓存 2.3. 语法解析(Parser) 2.4、执行sql 1. 预处理(Preprocessor) 2. 查询优化器(Optimizer) 3. 执行器…...

基于PHP的连锁酒店管理系统
有需要请加文章底部Q哦 可远程调试 基于PHP的连锁酒店管理系统 一 介绍 连锁酒店管理系统基于原生PHP开发,数据库mysql,前端bootstrap。系统角色分为用户和管理员。 技术栈 phpmysqlbootstrapphpstudyvscode 二 功能 用户 1 注册/登录/注销 2 个人中…...

CVPR2025重磅突破:AnomalyAny框架实现单样本生成逼真异常数据,破解视觉检测瓶颈!
本文介绍了一种名为AnomalyAny的创新框架,该方法利用Stable Diffusion的强大生成能力,仅需单个正常样本和文本描述,即可生成逼真且多样化的异常样本,有效解决了视觉异常检测中异常样本稀缺的难题,为工业质检、医疗影像…...

认识CMake并使用CMake构建自己的第一个项目
1.CMake的作用和优势 跨平台支持:CMake支持多种操作系统和编译器,使用同一份构建配置可以在不同的环境中使用 简化配置:通过CMakeLists.txt文件,用户可以定义项目结构、依赖项、编译选项等,无需手动编写复杂的构建脚本…...

实战设计模式之模板方法模式
概述 模板方法模式定义了一个操作中的算法骨架,并将某些步骤延迟到子类中实现。模板方法使得子类可以在不改变算法结构的前提下,重新定义算法中的某些步骤。简单来说,就是在一个方法中定义了要执行的步骤顺序或算法框架,但允许子类…...
