121. 买卖股票的最佳时机
题目描述
给定一个数组 prices ,它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。
你只能选择 某一天 买入这只股票,并选择在 未来的某一个不同的日子 卖出该股票。设计一个算法来计算你所能获取的最大利润。
返回你可以从这笔交易中获取的最大利润。如果你不能获取任何利润,返回 0 。
示例 1:
输入:[7,1,5,3,6,4]
输出:5
解释:在第 2 天(股票价格 = 1)的时候买入,在第 5 天(股票价格 = 6)的时候卖出,最大利润 = 6-1 = 5 。注意利润不能是 7-1 = 6, 因为卖出价格需要大于买入价格;同时,你不能在买入前卖出股票。
示例 2:
输入:prices = [7,6,4,3,1]
输出:0
解释:在这种情况下, 没有交易完成, 所以最大利润为 0。
提示:
1 <= prices.length <= 1050 <= prices[i] <= 104
解答
class Solution {
public:int maxProfit(vector<int>& prices) {// 贪心法取最左最小值和最右最大值int low = INT_MAX;int res = 0;for(int i = 0; i < prices.size(); ++i){low = min(low, prices[i]);res = max(res, prices[i] - low);} return res;}int maxProfit1(vector<int>& prices) {// dp[i][0] 表示第i天持有可获得的最大利润// dp[i][1] 表示第i天不持有可获得的最大利润vector<vector<int>> dp(prices.size(), vector<int>(2, 0));// 第i天持有股票所得最多现金dp[i][0]有两种情况// case1:第i-1天就持有,则保持现状为 dp[i - 1][0]// case1:第i-1天未持有,则当天买入 -prices[i]// 得 dp[i][0] = max(dp[i - 1][0], - prices[i]);// 第i天不持有股票所得最多现金dp[i][1]有两种情况// case1:第i-1天持有,则当天卖出 dp[i - 1][0] + prices[i]// case1:第i-1天未持有,则保持现状 dp[i - 1][1]// 故得:dp[i][1] = max(dp[i - 1][1], dp[i - 1][0] + prices[i]);dp[0][0] = -prices[0];dp[0][1] = 0;for(int i = 1; i < prices.size(); ++i){dp[i][0] = max(dp[i - 1][0], -prices[i]);dp[i][1] = max(dp[i - 1][0] + prices[i], dp[i - 1][1]);}// 最后一天不持有所得最大现金return dp[prices.size() - 1][1];}
};
相关文章:

121. 买卖股票的最佳时机
题目描述 给定一个数组 prices ,它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。 你只能选择 某一天 买入这只股票,并选择在 未来的某一个不同的日子 卖出该股票。设计一个算法来计算你所能获取的最大利润。 返回你可以从这笔交易中获取的…...
 LTO(Link-Time Optimization))
FDO(Feedback-Driven Optimization) LTO(Link-Time Optimization)
反馈驱动优化(Feedback-Driven Optimization,FDO)和链接时优化(Link-Time Optimization,LTO)是两种重要的编译器优化技术。下面我们详细介绍这两种技术: 反馈驱动优化 (FDO): FDO 是…...

低成本无刷高速吹风机单片机方案
高速吹风机的转速一般是普通吹风机的5倍左右。一般来说,吹风机的电机转速一般为2-3万转/分钟,而高速吹风机的电机转速一般为10万转/分钟左右。高转速增加了高风速。一般来说,吹风机的风力只有12-17米/秒,而高速吹风机的风力可以达…...

使用Python爬取某查查APP端(Appium自动化篇)
1. 写在前面 某查查网站反爬虫风控还是较强的,之后会分别介绍一下PC端协议、APP端自动化、APP端接口协议三种采集方案。这里主要介绍APP端的自动化方式,APP端自动化方式需要登陆账号,协议的话需要签名授权(自动化经测试没有太多限…...

vue3实现组件可拖拽 vuedraggable
npm i -S vuedraggablenext 中文文档,里面有完整代码案例,值得一看 vue.draggable vue3 版本在工作台中的应用场景 - itxst.com...

gradio常用组件
gradio常用组件 1.gradio程序启动2.写入html相关代码3.文本框4. 回车触发事件5.选择按钮框6.下拉框7.点击按钮8.清空按钮9.监听组件10.输出流11.template 1.gradio程序启动 import gradio as gr def tab():pass with gr.Blocks() as ui:gr.Markdown("# <center>&am…...
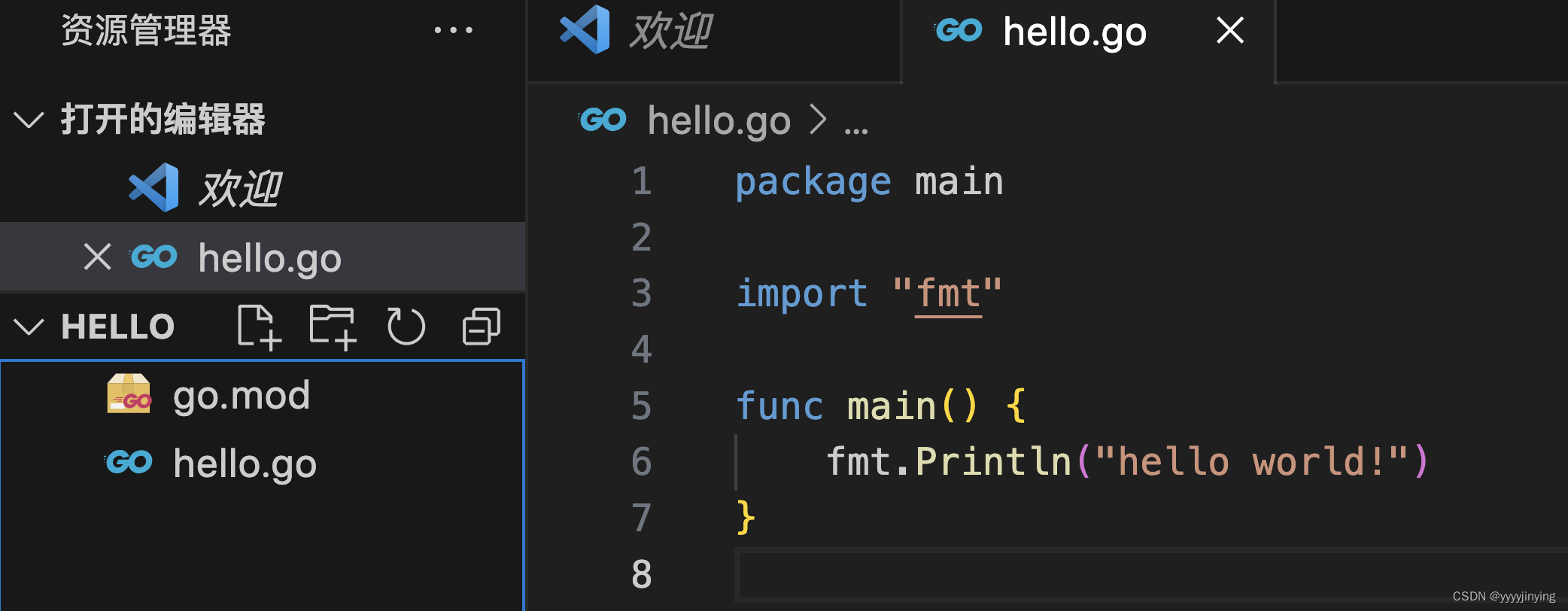
vcode开发go
配置环境变量 go env -w GO111MODULEon go env -w GOPROXYhttps://goproxy.cn,direct 创建文件夹 mkdir hello cd hello go mod help go mod help 初始化一个项目 go mod init hello 获取第三方包 go get github.com/shopspring/decimal 将依赖包下载到本地 go mod …...

聊城大学823软件工程考研
1.什么是软件工程?它目标和内容是什么? 软件工程就是用科学的知识和技术原理来定义,开发,维护软件的一门学科。 软件工程目标:付出较低开发成本;达到要求的功能;取得较好的性能;开发的软件易于移植&…...
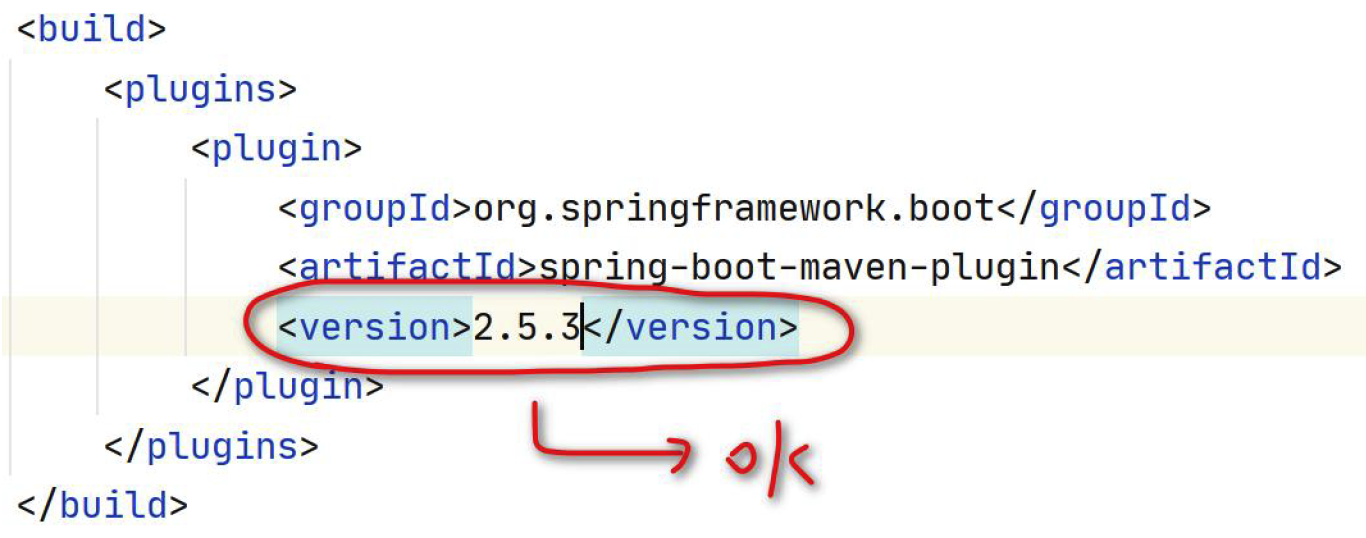
Spring Initailizr--快速入门--SpringBoot的选择
😀前言 本篇博文是关于IDEA使用Spring Initializer快速创建Spring Boot项目的说明,希望能够帮助到您😊 🏠个人主页:晨犀主页 🧑个人简介:大家好,我是晨犀,希望我的文章可…...

大数据课程I1——Kafka的概述
文章作者邮箱:yugongshiye@sina.cn 地址:广东惠州 ▲ 本章节目的 ⚪ 了解Kafka的概念; ⚪ 掌握Kafka的配置与启动; 一、简介 1. 基本概念 Apache kafka 是一个分布式数据流平台。可以从如下几个层面来理解: 1. 我们可以向Kafka发布数据以及从Kafka订阅…...

视图簇 se54 sm34 se54
今天演练了一下 维护视图到视图簇的过程。 se11建表,建表之后 【使用程序】→【表维护生成器】 se54 新建视图簇 对象结构 选中其中一行 字段附属 PS:以上每一行都要设置过去 , 设置完成了 激活 sm34展示...

风丘科技将亮相 EVM ASIA 2023
风丘科技将首次亮相 EVM ASIA 2023 WINDHILL will debut EVM ASIA 2023 ——可持续移动的未来 —The Future of SUSTAINABLE Mobility EVM ASIA 2023是亚太地区电气化的国际性展会,专注于新能源汽车、充电技术及汽车零件制造等。展会致力于促进包括充电站、交通…...

腾讯云服务器S6、SA3、S5、SA2等CVM实例介绍
腾讯云服务器CVM实例标准型S6、SA3、S5、SA2等多款实例降价,最高幅度达40%,标准型S6云服务器是新一代云服务器,SA3和SA2是AMD处理器,标准型S5是次新一代的云服务器,如下图: 腾讯云服务器CVM降价 标准型S6&a…...

使用kickstart和anaconda自动化安装centos系统
使用kickstart和anaconda自动化安装centos系统 使用kickstart和anaconda自动化安装centos系统 anaconda 介绍 kickstart 介绍 实验过程 前提 1.已经安装好至少两台centos系统 2.需要实现自动安装的系统的光盘镜像 3.已安装的系统之间可以通讯(比如处于VMware中的NAT网络的…...
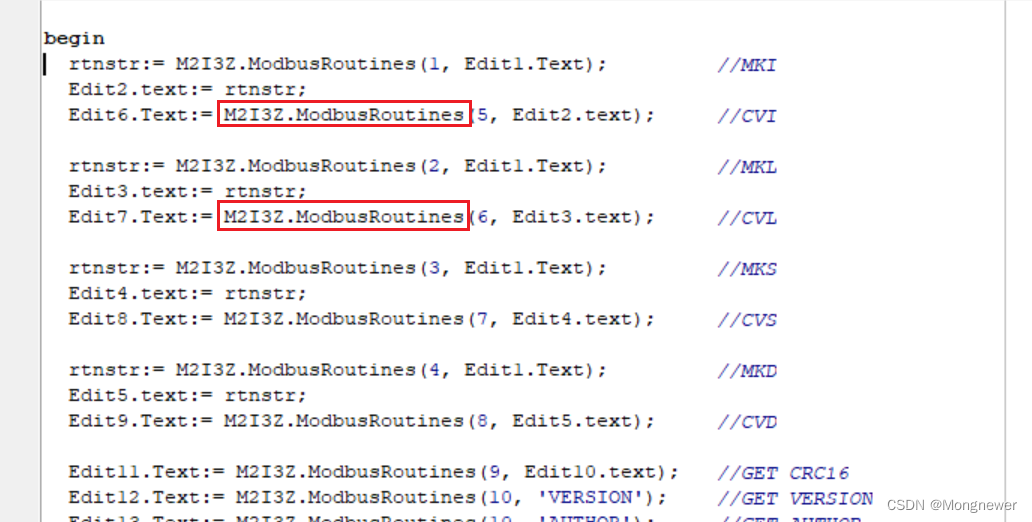
Delphi7通过VB6之COM对象调用PowerBASIC写的DLL功能
Delphi7通过VB6之COM对象调用PowerBASIC写的DLL功能。标题挺长,其实目标很简单,就是在Delphi7中使用PowerBASIC的MKI/CVI, MKS/CVS, MKD/CVD,并顺便加入CRC16检验函数,再进行16进制高低字节调整,方便在VB6、Delphi、La…...

中电金信:ChatGPT一夜爆火,知识图谱何以应战?
随着ChatGPT的爆火出圈 人工智能再次迎来发展小高潮 那么作为此前搜索领域的主流技术 知识图谱前路又将如何呢? 事实上,ChatGPT也并非“万能”,作为黑箱模型,ChatGPT很难验证生成的知识是否准确。并且ChatGPT是通过概率模型执行推…...

单细胞分类和预测任务
对于分类和预测任务,在生物信息学领域有一些常用的方法和工具可以使用。以下是一些常见的方法和工具: 1. 机器学习方法: 包括支持向量机(Support Vector Machine,SVM)、随机森林(Random Forest…...

那些年的Webview开发经验记录
获取网站视频真实链接 直接上工具类 直接调用即可,这个工具类会返回加载的网页中所有的链接,至于对链接怎么处理就是你们自己的事了, 亲测至今我所遇到的所有视频,它都可以捕获到其链接 import android.app.Activity; import an…...

ssh-keygen详解
ssh-keygen命令参数详解 -b BITS指定密钥长度。 -e读取私有或公共 OpenSSH 密钥文件并以 -m 选项指定的格式之一将密钥打印到标准输出。 -C添加注释。 -f FILENAME指定用来保存密钥的文件名。 -i以 -m 选项指定的格式读取未加密的私钥(或公钥)文件&…...
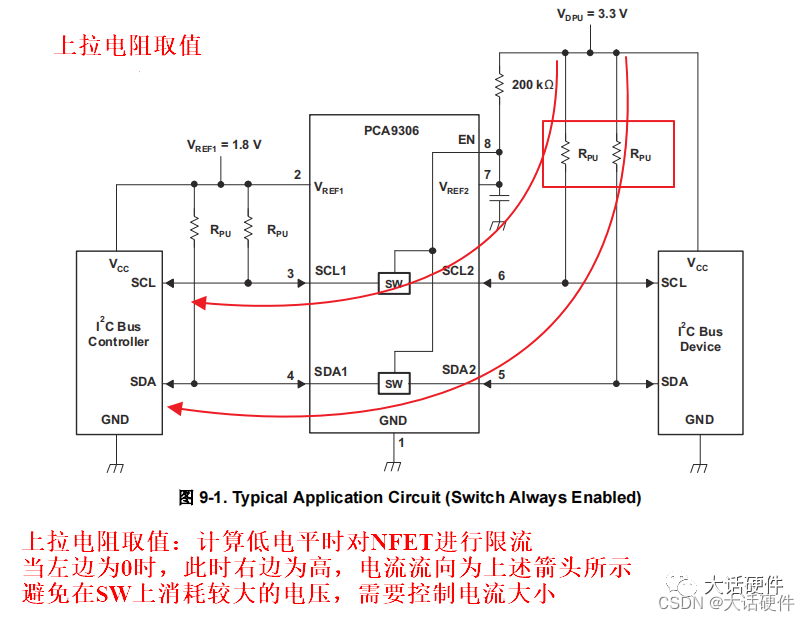
自动方向识别式 LSF型电平转换芯片
大家好,这里是大话硬件。 今天这篇文章想分享一下电平转换芯片相关的内容。 其实在之前的文章分享过一篇关于电平转换芯片的相关内容,具体可以看链接《高速电路逻辑电平转换设计》。当时这篇文章也是分析的电平转换芯片,不过那时候更多的是…...

stm32G473的flash模式是单bank还是双bank?
今天突然有人stm32G473的flash模式是单bank还是双bank?由于时间太久,我真忘记了。搜搜发现,还真有人和我一样。见下面的链接:https://shequ.stmicroelectronics.cn/forum.php?modviewthread&tid644563 根据STM32G4系列参考手…...
)
React Native 开发环境搭建(全平台详解)
React Native 开发环境搭建(全平台详解) 在开始使用 React Native 开发移动应用之前,正确设置开发环境是至关重要的一步。本文将为你提供一份全面的指南,涵盖 macOS 和 Windows 平台的配置步骤,如何在 Android 和 iOS…...

智慧工地云平台源码,基于微服务架构+Java+Spring Cloud +UniApp +MySql
智慧工地管理云平台系统,智慧工地全套源码,java版智慧工地源码,支持PC端、大屏端、移动端。 智慧工地聚焦建筑行业的市场需求,提供“平台网络终端”的整体解决方案,提供劳务管理、视频管理、智能监测、绿色施工、安全管…...

【Web 进阶篇】优雅的接口设计:统一响应、全局异常处理与参数校验
系列回顾: 在上一篇中,我们成功地为应用集成了数据库,并使用 Spring Data JPA 实现了基本的 CRUD API。我们的应用现在能“记忆”数据了!但是,如果你仔细审视那些 API,会发现它们还很“粗糙”:有…...

基于Java+MySQL实现(GUI)客户管理系统
客户资料管理系统的设计与实现 第一章 需求分析 1.1 需求总体介绍 本项目为了方便维护客户信息为了方便维护客户信息,对客户进行统一管理,可以把所有客户信息录入系统,进行维护和统计功能。可通过文件的方式保存相关录入数据,对…...

基于SpringBoot在线拍卖系统的设计和实现
摘 要 随着社会的发展,社会的各行各业都在利用信息化时代的优势。计算机的优势和普及使得各种信息系统的开发成为必需。 在线拍卖系统,主要的模块包括管理员;首页、个人中心、用户管理、商品类型管理、拍卖商品管理、历史竞拍管理、竞拍订单…...

JavaScript 数据类型详解
JavaScript 数据类型详解 JavaScript 数据类型分为 原始类型(Primitive) 和 对象类型(Object) 两大类,共 8 种(ES11): 一、原始类型(7种) 1. undefined 定…...

Git 3天2K星标:Datawhale 的 Happy-LLM 项目介绍(附教程)
引言 在人工智能飞速发展的今天,大语言模型(Large Language Models, LLMs)已成为技术领域的焦点。从智能写作到代码生成,LLM 的应用场景不断扩展,深刻改变了我们的工作和生活方式。然而,理解这些模型的内部…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现企业微信功能
1. 开发环境准备 安装DevEco Studio 3.1: 从华为开发者官网下载最新版DevEco Studio安装HarmonyOS 5.0 SDK 项目配置: // module.json5 {"module": {"requestPermissions": [{"name": "ohos.permis…...
)
安卓基础(Java 和 Gradle 版本)
1. 设置项目的 JDK 版本 方法1:通过 Project Structure File → Project Structure... (或按 CtrlAltShiftS) 左侧选择 SDK Location 在 Gradle Settings 部分,设置 Gradle JDK 方法2:通过 Settings File → Settings... (或 CtrlAltS)…...
