机器人静力学与刚度模型学习笔记
总算进行到刚度模型了。。。
❤ 2023.8.6 ❤
机器人静力学
学习资料
→→→【4-10机器人的静力分析】
机器人末端广义力
F = [ f m ] = [ f x f y f z m x m y m z ] F=\left[\begin{matrix}f\\m\\\end{matrix}\right]=\left[\begin{matrix}f_x\\f_y\\f_z\\m_x\\m_y\\m_z\\\end{matrix}\right] F=[fm]= fxfyfzmxmymz
机器人关节力矩矢量
τ = [ τ 1 τ 2 … τ n ] T \tau=\left[\begin{matrix}\tau_1&\tau_2&\ldots&\tau_n\\\end{matrix}\right]^\mathrm{T} τ=[τ1τ2…τn]T
根据虚功与虚位移原理
τ T Δ q = τ 1 Δ q 1 + τ 1 Δ q 1 + … + τ n Δ q n = f T d + m T φ = F T D \tau^\mathrm{T}\Delta q=\tau_1\Delta q_1+\tau_1\Delta q_1+\ldots+\tau_n\Delta q_n=f^\mathrm{T}d+m^\mathrm{T}\varphi=F^\mathrm{T}D τTΔq=τ1Δq1+τ1Δq1+…+τnΔqn=fTd+mTφ=FTD
又
D = J ( q ) d q D=J\left(q\right)dq D=J(q)dq
于是不计关节摩擦和杆件重力,其关系为
τ = J T F \tau=J^\mathrm{T}F τ=JTF
这里 J T F J^\mathrm{T}F JTF为机器人力雅可比矩阵,是速度雅可比矩阵的转秩
机器人刚度模型
6轴机器人关节刚度
K θ = d i a g ( [ K 1 , K 2 , K 3 , K 4 , K 5 , K 6 ] ) K_\theta=diag\left(\left[K_1,K_2,K_3,K_4,K_5,K_6\right]\right) Kθ=diag([K1,K2,K3,K4,K5,K6])
在末端力作用下,关节变形为
d q = K θ − 1 ⋅ τ = K θ − 1 ⋅ J T ⋅ F dq=K_\theta^{-1}\cdot\tau=K_\theta^{-1}\cdot J^\mathrm{T}\cdot F dq=Kθ−1⋅τ=Kθ−1⋅JT⋅F
于是机器人末端偏移量
Δ X = J ⋅ d q = J K θ − 1 J T F \Delta X=J\cdot d_q=JK_\theta^{-1}J^\mathrm{T}F ΔX=J⋅dq=JKθ−1JTF
Δ X = [ Δ d Δ φ ] \Delta X=\left[\begin{matrix}\Delta d\\\Delta\varphi\\\end{matrix}\right] ΔX=[ΔdΔφ]
Δ d \Delta d Δd——机器人末端位置偏移
Δ φ \Delta\varphi Δφ——机器人末端姿态偏移
相关文章:

机器人静力学与刚度模型学习笔记
总算进行到刚度模型了。。。 ❤ 2023.8.6 ❤ 机器人静力学 学习资料 →→→【4-10机器人的静力分析】 机器人末端广义力 F [ f m ] [ f x f y f z m x m y m z ] F\left[\begin{matrix}f\\m\\\end{matrix}\right]\left[\begin{matrix}f_x\\f_y\\f_z\\m_x\\m_y\\m_z\\\end{…...

geeemap学习总结(1)——Anaconda-VSCode-geemap环境安装与配置
配置conda geemap 环境 通过Anaconda配置geemap环境较为方便,首先需在系统中完成 Anaconda安装。创建名为geemap的环境conda create -n geemap切换到新建的环境conda activate geemap安装geemap依赖包conda install -c conda-forge geemap 安装mambaconda install …...
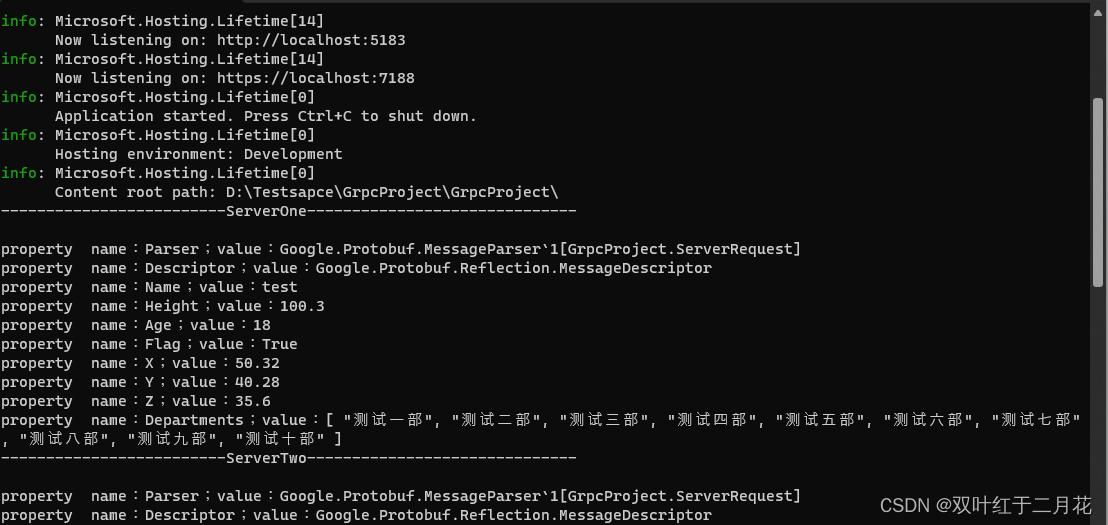
.netcore grpc一元方法详解
一、grpc服务端搭建 打开visual studio--》新建项目--》创建ASP.NET Core gRPC服务。 这里我是用的.NET 6.0做为底层框架,使用该框架支持grpc的功能更全面。令注使用nuget包Grpc.AspNetCore这里我使用的是2.40.0版本。 // 创建dollar.proto文件syntax "prot…...

自学网络安全(黑客)全网详细路线
前言 web渗透是网络安全大行业里入门板块,就像十年前的软件,前景非常被看好,薪资也很诱人。与软件测试和前端开发只需掌握一定的编程能力不同的是,渗透需要掌握的知识内容较多,花费的时间较长,渗透测试掌握…...
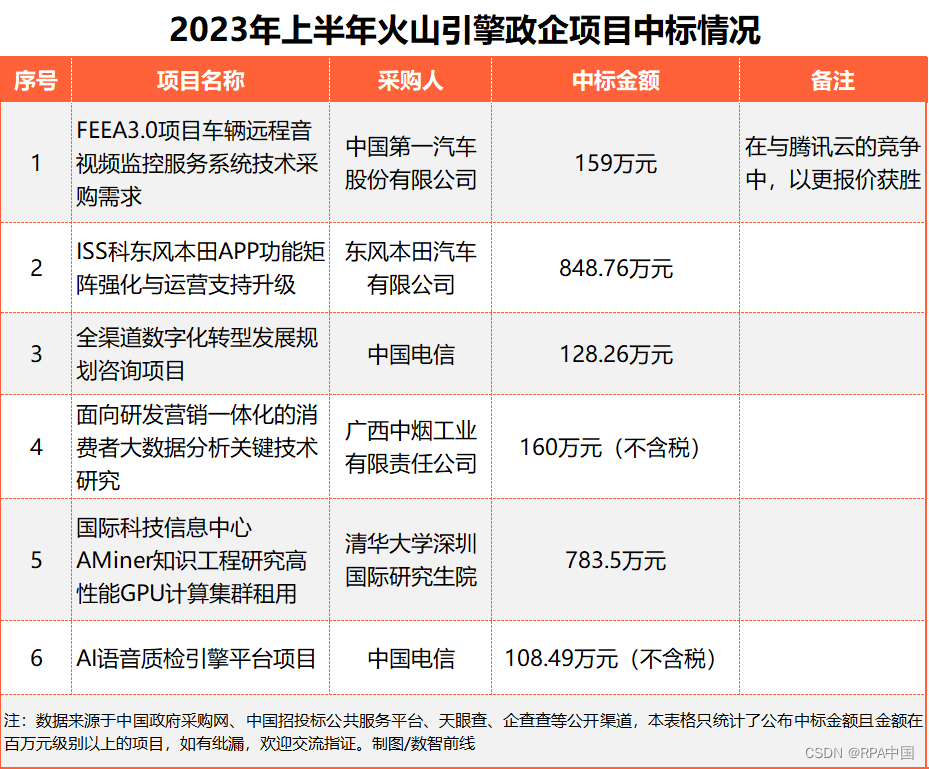
上半年210个数字化大单,花落谁家?
2023年,各地数字化采购项目有怎样的进展?最近,我们通过中国政府采购网、中国招投标公共服务平台、天眼查、企查查等渠道,梳理了2023年上半年政企数字化项目的中标情况,并从中看到今年数字化项目的市场特点。 01 金融千…...
)
Integer.bitCount()
先看一道算法题: 剑指 Offer 15. 二进制中1的个数 编写一个函数,输入是一个无符号整数(以二进制串的形式),返回其二进制表达式中数字位数为 1 的个数(也被称为 汉明重量).)。 提示: …...
【Gitee的使用】Gitee的简单使用,查看/创建SSH公匙、创建版本库、拉取代码、提交代码
推荐阅读 CSDN主页GitHub开源地址Unity3D插件分享简书地址我的个人博客 大家好,我是佛系工程师☆恬静的小魔龙☆,不定时更新Unity开发技巧,觉得有用记得一键三连哦。 一、前言 本篇文章简单介绍,如何在Gitee上面创建版本库、拉取…...

Java 跨平台多媒体处理样例
代码 import cn.hutool.core.exceptions.ExceptionUtil; import cn.hutool.core.io.FileUtil; import cn.hutool.core.io.IoUtil; import cn.hutool.core.util.CharsetUtil; import lombok.extern.slf4j.Slf4j; import ws.schild.jave.Encoder; import ws.schild.jave.Multime…...
——安装)
cmake基础(3)——安装
一、简介 install命令用于指定安装时的规则,由于安装命令比较复杂,这里做一部分内容的介绍,后续用到再继续完善。 1.命令简介 本文档基于3.20,目前有6种安装方式。 install(TARGETS <target>... [...]) install({FILES …...
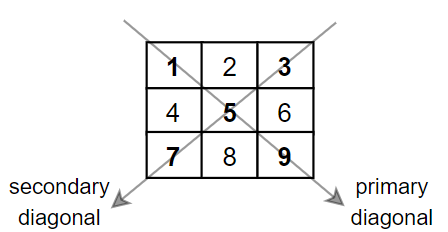
LeetCode解法汇总1572. 矩阵对角线元素的和
目录链接: 力扣编程题-解法汇总_分享记录-CSDN博客 GitHub同步刷题项目: https://github.com/September26/java-algorithms 原题链接:力扣(LeetCode)官网 - 全球极客挚爱的技术成长平台 描述: 给你一个正…...
)
BFC(Block formatting context 块级格式化上下文)
1、开启了BFC能解决什么问题? 给父元素开启BFC,其子元素不会再产生 margin 塌陷问题。自己不会被其他浮动元素所覆盖。就算其子元素浮动,元素自身高度也不会塌陷。 2、如何开启? 根元素浮动元素绝对定位、固定定位的元素行内块…...
Leetcode-每日一题【剑指 Offer 14- II. 剪绳子 II】
题目 2、3、3的三段,此时得到的最大乘积是18。 答案需要取模 1e97(1000000007),如计算初始结果为:1000000008,请返回 1。 示例 1: 输入: 2输出: 1解释: 2 1 1, 1 1 1 示例 2: 输入: 10输出…...
bye 我的博客网站
Bye🙋🙋🙋,我的博客网站。在我的服务器上运行了9个月之久的博客网站要和大家Bye了。 背景 可能很多人不知道我的这个博客网站的存在,好吧,最后一次展示它了,博客网站地址在这里,它…...
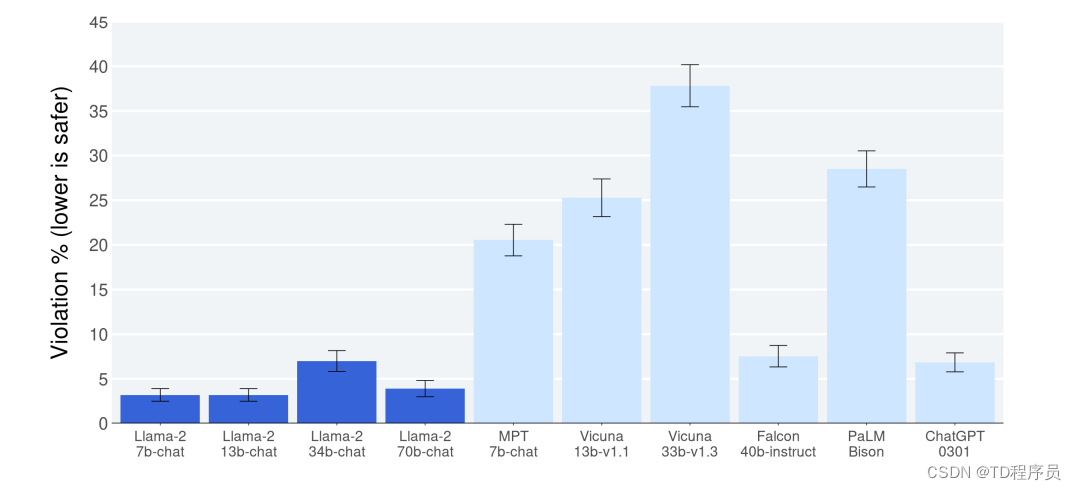
Llama 2:开放基础和微调聊天模型
介绍 大型语言模型(llm)作为高能力的人工智能助手,在复杂的推理任务中表现出色,这些任务需要广泛领域的专家知识,包括编程和创意写作等专业领域。它们可以通过直观的聊天界面与人类进行交互,这在公众中得到了迅速而广泛的采用。 法学硕士的能力是显著的考虑到训练的表面上…...
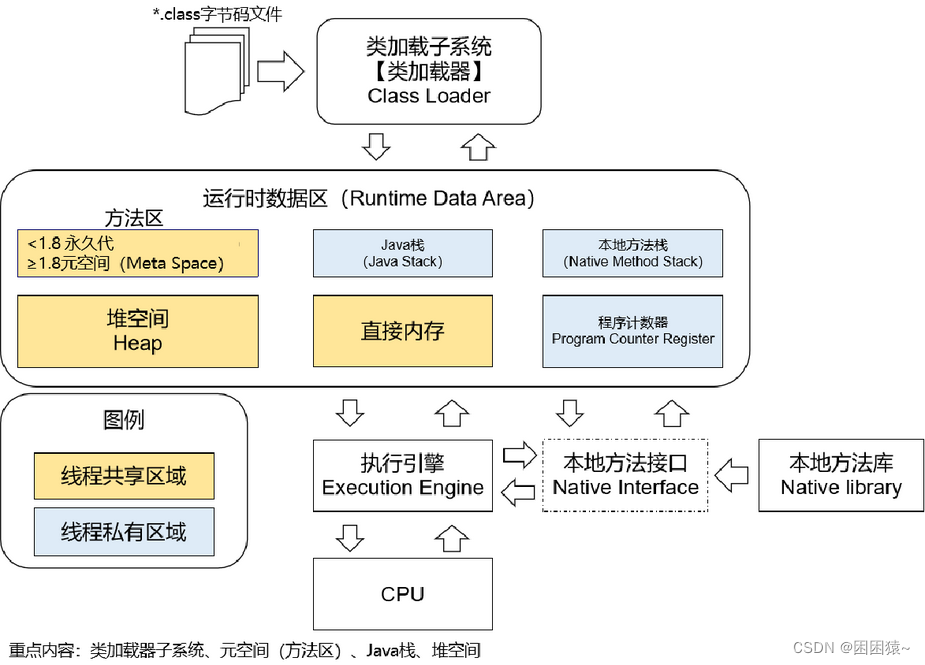
JVM工作的总体机制概述
JDK、JRE、JVM关系回顾 JVM:Java Virtual Machine,翻译过来是Java虚拟机JRE:Java Runtime Environment,翻译过来是Java运行时环境 JREJVMJava程序运行时所需要的类库JDK:Java Development Kits,翻译过来是…...
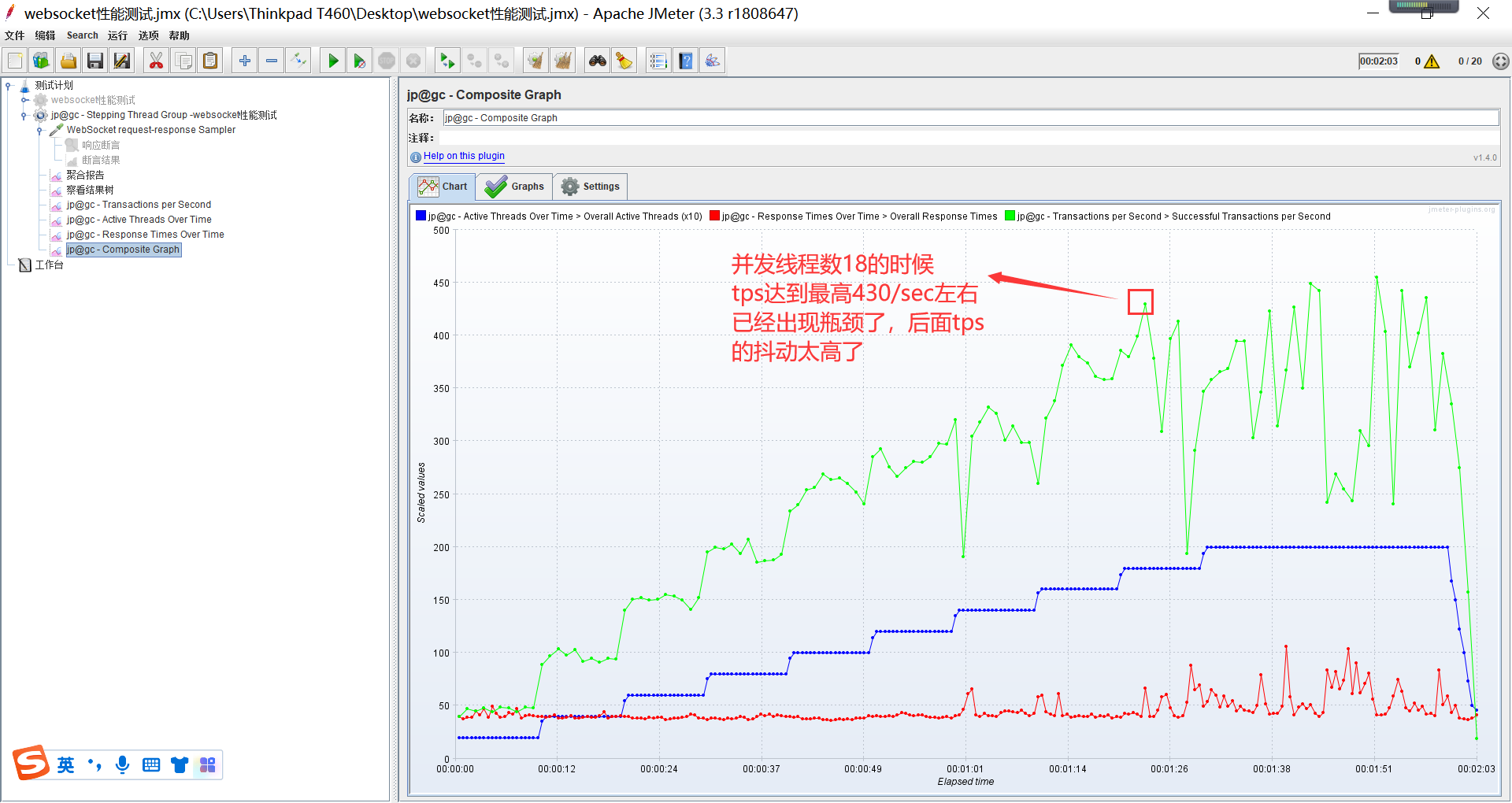
jmeter工具测试和压测websocket协议【杭州多测师_王sir】
一、安装JDK配置好环境变量,安装好jmeter 二、下载WebSocketSampler发送请求用的,地址:https://bitbucket.org/pjtr/jmeter-websocket-samplers/downloads/?spma2c4g.11186623.2.15.363f211bH03KeI 下载解压后的jar包放到D:\JMeter\apache-j…...

国产漏洞扫描器Xray入门,详细教程
国产漏洞扫描器Xray入门,详细教程 1.Xray简介2.快速开始3.使用 xray 代理模式进行漏洞扫描4.使用 xray 基础爬虫模式进行漏洞扫描5.使用 xray 进行服务扫描1.Xray简介 xray 是一款功能强大的安全评估工具,由多名经验丰富的一线安全从业者呕心打造而成,主要特性有: 检测速度…...
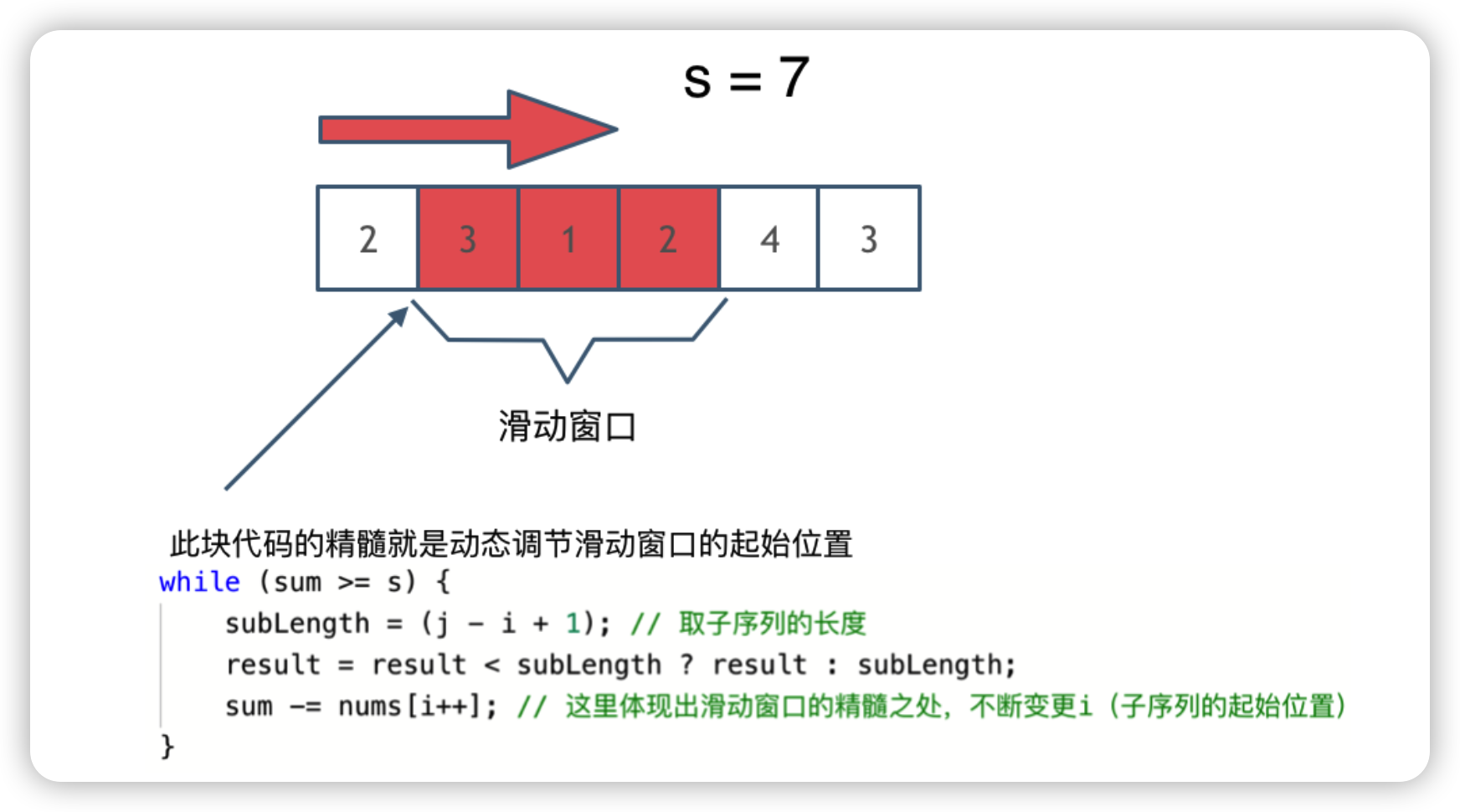
LeetCode209. 长度最小的子数组
题目:LeetCode209. 长度最小的子数组 描述: 给定一个含有 n 个正整数的数组和一个正整数 target 。 找出该数组中满足其和 ≥ target 的长度最小的 连续子数组 [numsl, numsl1, …, numsr-1, numsr] ,并返回其长度。如果不存在符合条件的子…...

css冒号对齐
实现后的样式效果 实现方式 html: <el-col v-if"item.showInSingle ! false" :span"6" style"padding: 4px 0"><label>{{ item.label }}:</label><span v-if"singleData[item.prop] ! 0 &…...

那些年的golang开发经验记录
goland 问题CreateProcess error216, 该版本的 %1 与你运行的 Windows 版本不兼容。请查看计算机的系统信息,然后联系软件发布者 Cannot run program "......" (in directory "D:\project\go\awesomeProject\src\test"): CreateProcess error2…...

家政维修平台实战20:权限设计
目录 1 获取工人信息2 搭建工人入口3 权限判断总结 目前我们已经搭建好了基础的用户体系,主要是分成几个表,用户表我们是记录用户的基础信息,包括手机、昵称、头像。而工人和员工各有各的表。那么就有一个问题,不同的角色…...

React19源码系列之 事件插件系统
事件类别 事件类型 定义 文档 Event Event 接口表示在 EventTarget 上出现的事件。 Event - Web API | MDN UIEvent UIEvent 接口表示简单的用户界面事件。 UIEvent - Web API | MDN KeyboardEvent KeyboardEvent 对象描述了用户与键盘的交互。 KeyboardEvent - Web…...

ESP32 I2S音频总线学习笔记(四): INMP441采集音频并实时播放
简介 前面两期文章我们介绍了I2S的读取和写入,一个是通过INMP441麦克风模块采集音频,一个是通过PCM5102A模块播放音频,那如果我们将两者结合起来,将麦克风采集到的音频通过PCM5102A播放,是不是就可以做一个扩音器了呢…...

IoT/HCIP实验-3/LiteOS操作系统内核实验(任务、内存、信号量、CMSIS..)
文章目录 概述HelloWorld 工程C/C配置编译器主配置Makefile脚本烧录器主配置运行结果程序调用栈 任务管理实验实验结果osal 系统适配层osal_task_create 其他实验实验源码内存管理实验互斥锁实验信号量实验 CMISIS接口实验还是得JlINKCMSIS 简介LiteOS->CMSIS任务间消息交互…...

自然语言处理——循环神经网络
自然语言处理——循环神经网络 循环神经网络应用到基于机器学习的自然语言处理任务序列到类别同步的序列到序列模式异步的序列到序列模式 参数学习和长程依赖问题基于门控的循环神经网络门控循环单元(GRU)长短期记忆神经网络(LSTM)…...

稳定币的深度剖析与展望
一、引言 在当今数字化浪潮席卷全球的时代,加密货币作为一种新兴的金融现象,正以前所未有的速度改变着我们对传统货币和金融体系的认知。然而,加密货币市场的高度波动性却成为了其广泛应用和普及的一大障碍。在这样的背景下,稳定…...

GruntJS-前端自动化任务运行器从入门到实战
Grunt 完全指南:从入门到实战 一、Grunt 是什么? Grunt是一个基于 Node.js 的前端自动化任务运行器,主要用于自动化执行项目开发中重复性高的任务,例如文件压缩、代码编译、语法检查、单元测试、文件合并等。通过配置简洁的任务…...
免费数学几何作图web平台
光锐软件免费数学工具,maths,数学制图,数学作图,几何作图,几何,AR开发,AR教育,增强现实,软件公司,XR,MR,VR,虚拟仿真,虚拟现实,混合现实,教育科技产品,职业模拟培训,高保真VR场景,结构互动课件,元宇宙http://xaglare.c…...

多模态图像修复系统:基于深度学习的图片修复实现
多模态图像修复系统:基于深度学习的图片修复实现 1. 系统概述 本系统使用多模态大模型(Stable Diffusion Inpainting)实现图像修复功能,结合文本描述和图片输入,对指定区域进行内容修复。系统包含完整的数据处理、模型训练、推理部署流程。 import torch import numpy …...

C++ 设计模式 《小明的奶茶加料风波》
👨🎓 模式名称:装饰器模式(Decorator Pattern) 👦 小明最近上线了校园奶茶配送功能,业务火爆,大家都在加料: 有的同学要加波霸 🟤,有的要加椰果…...
