LeetCode209. 长度最小的子数组
题目:LeetCode209. 长度最小的子数组
描述:
给定一个含有 n 个正整数的数组和一个正整数 target 。
找出该数组中满足其和 ≥ target 的长度最小的 连续子数组 [numsl, numsl+1, …, numsr-1, numsr] ,并返回其长度。如果不存在符合条件的子数组,返回 0 。

思路:
滑动窗口
接下来就开始介绍数组操作中另一个重要的方法:滑动窗口。
所谓滑动窗口,就是不断的调节子序列的起始位置和终止位置,从而得出我们要想的结果。
在暴力解法中,是一个for循环滑动窗口的起始位置,一个for循环为滑动窗口的终止位置,用两个for循环 完成了一个不断搜索区间的过程。
那么滑动窗口如何用一个for循环来完成这个操作呢。
首先要思考 如果用一个for循环,那么应该表示 滑动窗口的起始位置,还是终止位置。
如果只用一个for循环来表示 滑动窗口的起始位置,那么如何遍历剩下的终止位置?
此时难免再次陷入 暴力解法的怪圈。
所以 只用一个for循环,那么这个循环的索引,一定是表示 滑动窗口的终止位置。
在本题中实现滑动窗口,主要确定如下三点:
窗口内是什么?
如何移动窗口的起始位置?
如何移动窗口的结束位置?
窗口就是 满足其和 ≥ s 的长度最小的 连续 子数组。
窗口的起始位置如何移动:如果当前窗口的值大于s了,窗口就要向前移动了(也就是该缩小了)。
窗口的结束位置如何移动:窗口的结束位置就是遍历数组的指针,也就是for循环里的索引。
解题的关键在于 窗口的起始位置如何移动,如图所示:
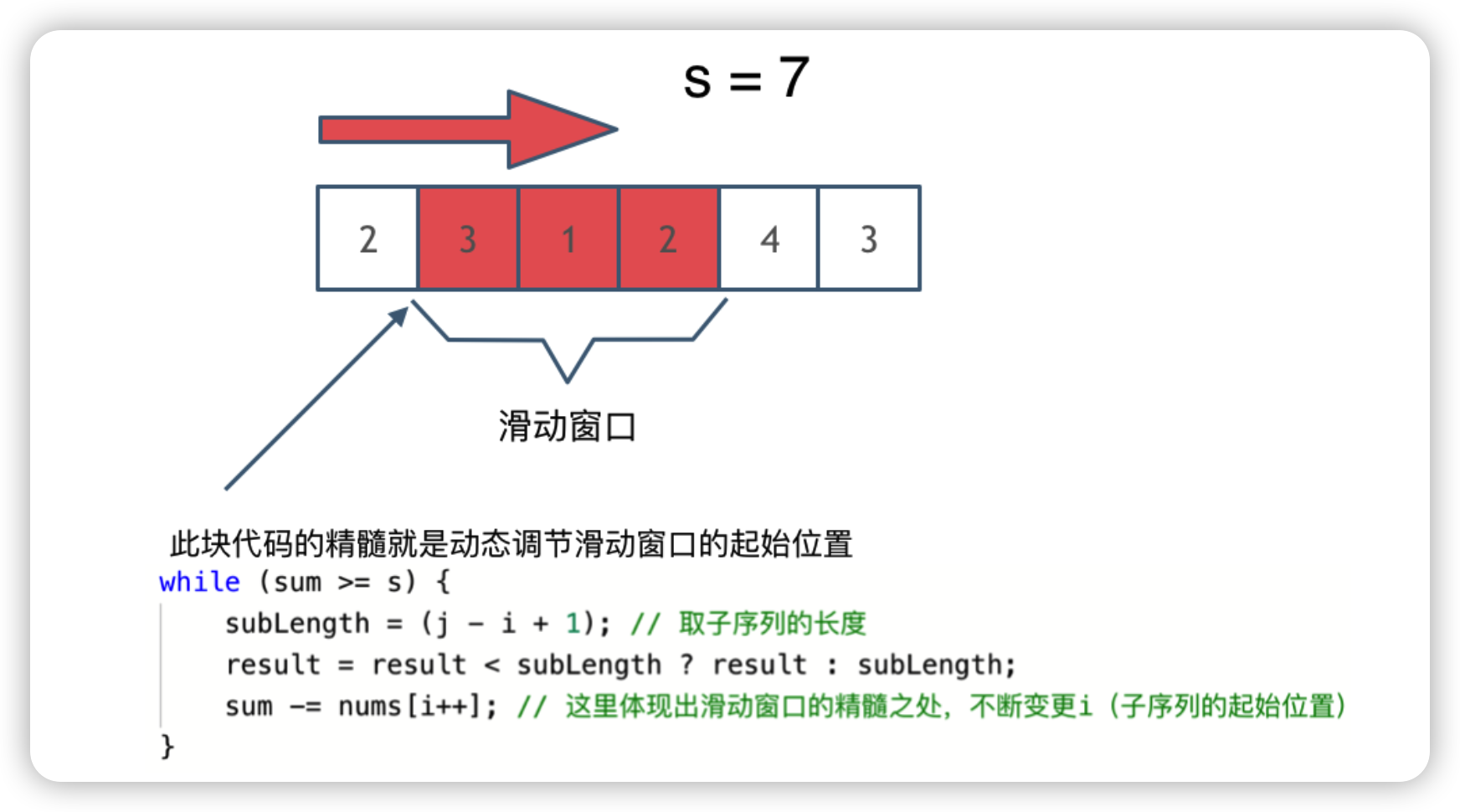
可以发现滑动窗口的精妙之处在于根据当前子序列和大小的情况,不断调节子序列的起始位置。从而将O(n^2)暴力解法降为O(n)。
public class Solution {public int minSubArrayLen(int target, int[] nums) {int i=0;int sum=0;int length=Integer.MAX_VALUE;for (int j = 0; j < nums.length; j++) {sum+=nums[j];while(sum>=target){length=(j-i+1)<length?(j-i+1):length;sum-=nums[i++];}}return length=length==Integer.MAX_VALUE?0:length;}
}
相关文章:

LeetCode209. 长度最小的子数组
题目:LeetCode209. 长度最小的子数组 描述: 给定一个含有 n 个正整数的数组和一个正整数 target 。 找出该数组中满足其和 ≥ target 的长度最小的 连续子数组 [numsl, numsl1, …, numsr-1, numsr] ,并返回其长度。如果不存在符合条件的子…...

css冒号对齐
实现后的样式效果 实现方式 html: <el-col v-if"item.showInSingle ! false" :span"6" style"padding: 4px 0"><label>{{ item.label }}:</label><span v-if"singleData[item.prop] ! 0 &…...

那些年的golang开发经验记录
goland 问题CreateProcess error216, 该版本的 %1 与你运行的 Windows 版本不兼容。请查看计算机的系统信息,然后联系软件发布者 Cannot run program "......" (in directory "D:\project\go\awesomeProject\src\test"): CreateProcess error2…...

element中select下拉框如何实现宽度自适应
简单暴力: element 和 elementPlus 都可以直接在el-select上添加 style"width: 100%" 解决 <el-select style"width: 100%" v-model"cats" multiple filterable placeholder"请选择分类"> . . . </el-select&…...

springboot项目get请求下划线转驼峰@JsonProperty注解失效问题
问题:解决sprigboot项目get请求中有下划线的入参参数,如:first_name,希望在项目中将下划线格式转成firstName,用JsonProperty注解发现失效问题 1.核查:JsonProperty注解对应包是否正确 正确包:…...
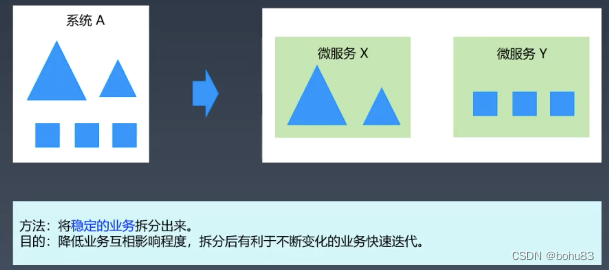
架构训练营学习笔记:6-2 微服务基础选型
基础选型 微服务基础设施架构 优先级 其中,核心 就是服务注册、服务发现、服务路由。 模式1-嵌入SDK 模式2-反向代理式 模式3-网络代理式(Service Mesh) 模式对比 常见微服务框架选择 嵌入SDK-dubbo Spring Cloud 反向代理式 APISIX …...
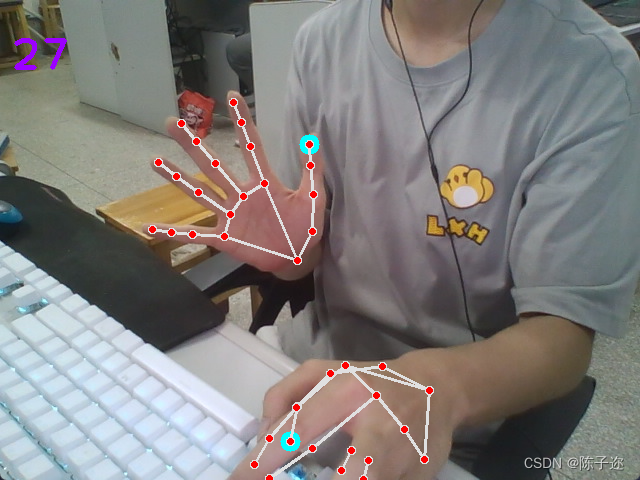
opencv实战项目 实现手势跟踪并返回位置信息(封装调用)
OpenCV 是一个基于 Apache2.0 许可(开源)发行的跨平台计算机视觉和机器学习软件库,可以运行在Linux、Windows、Android和Mac OS操作系统上。 需要提前准备opencv 和 mediapipe库 pip --default-timeout5000 install -i https://pypi.tuna.tsi…...

ElementUI动态添加表单项
昨天感冒发烧了,脑子不好使。在实现这个动态表单项时一直报错脑瓜子嗡嗡的! 不过好在昨天休息好了,今天起来趁脑瓜子好使,一会就弄好了。 这里记录一下 <el-form-itemv-for"(classId,index) in addFom.classIds":lab…...

Myatis和MybatisPlus常见分页方式
Myatis和MybatisPlus常见分页方式 一、mybaits 原生limit分页 SELECT * FROM order_info limit #{pageNow},#{pageSize}分页插件(ssm中,通过xml配置分页。springboot通过则通过配置文件) PageHelper插件:PageHelper.startPage(…...
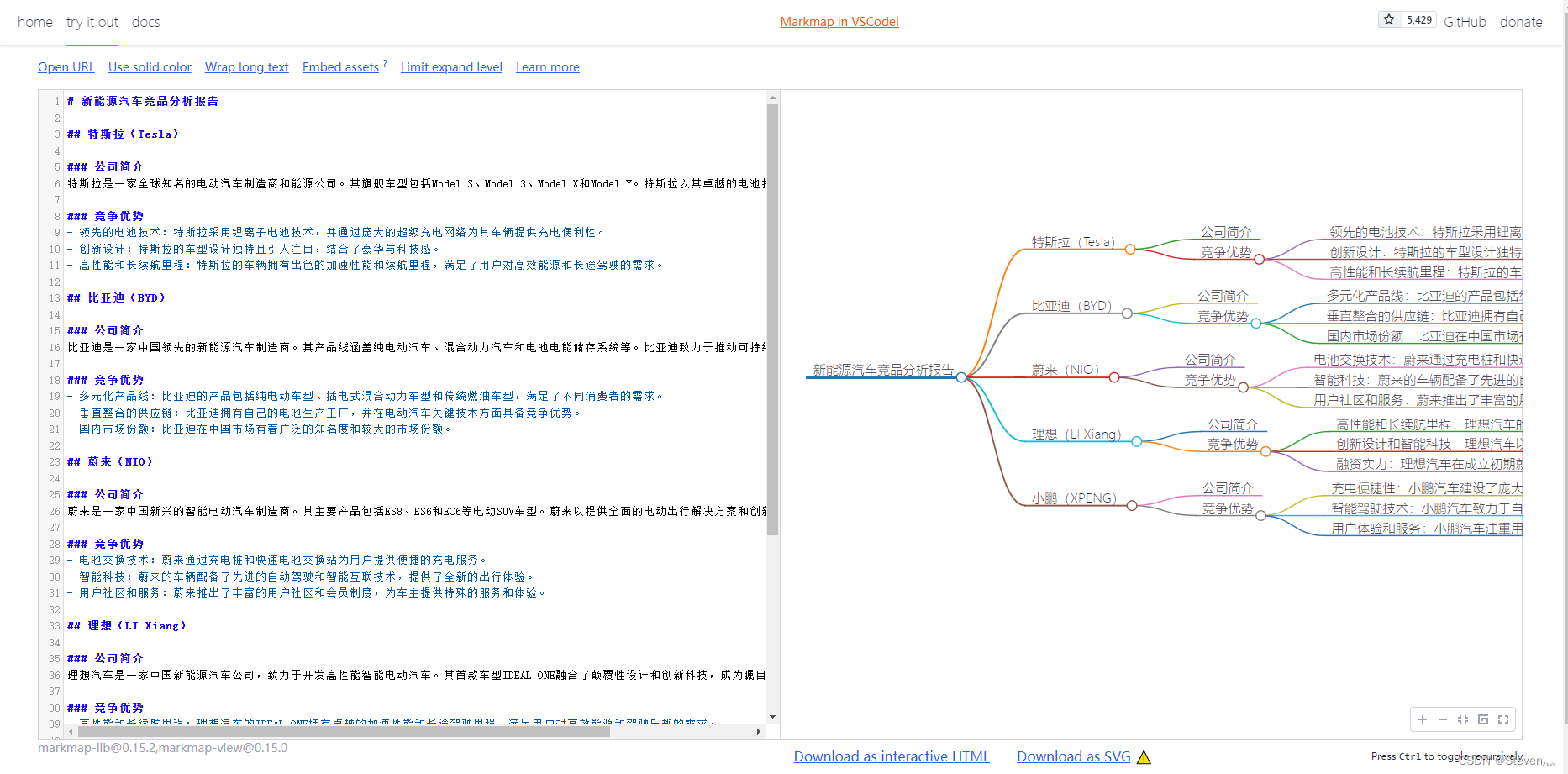
利用ChatGPT绘制思维导图——以新能源汽车竞品分析报告为例
随着人们对环境保护的日益关注和传统燃油汽车的限制,全球范围内对新能源汽车的需求不断增长。新能源汽车市场的激烈竞争使得了解各个竞品的特点和优劣成为关键。然而,针对这一领域的详尽竞品分析却常常需要大量时间和精力。 在此背景下,人工智…...
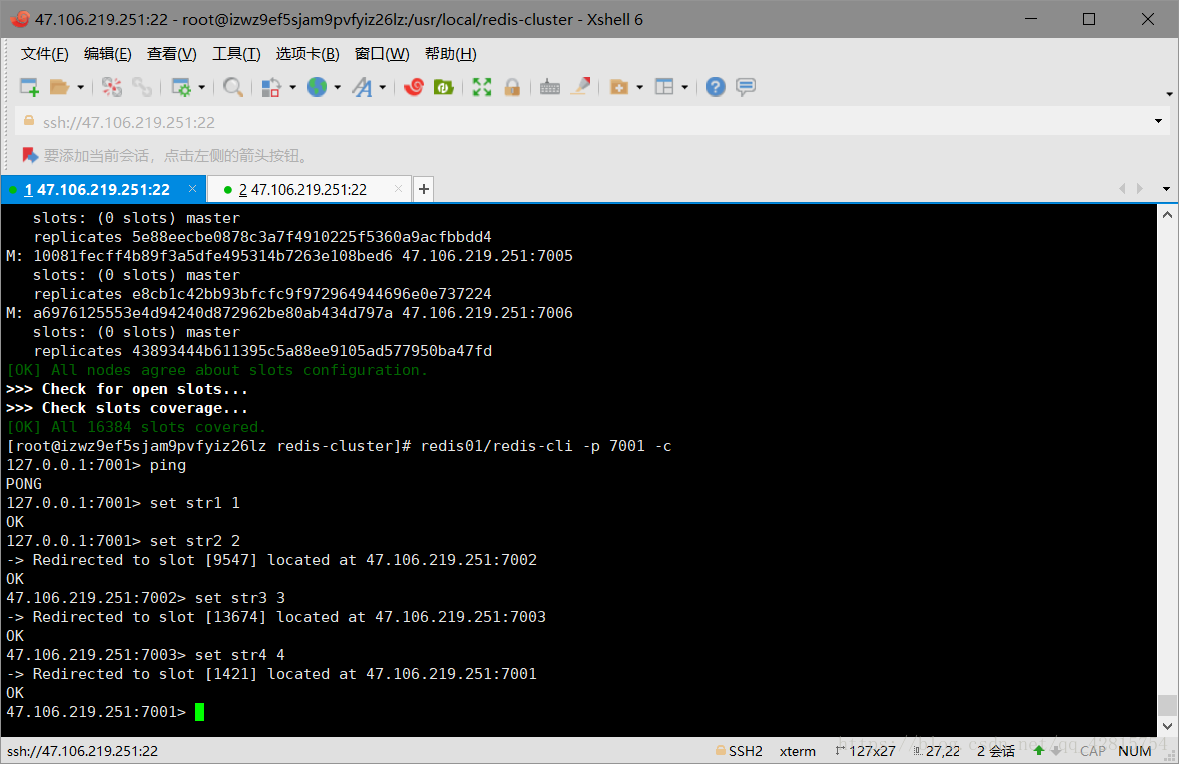
redis集群搭建(非常详细,适合新手)
免密登录脚本 #!/bin/bash # 检查是否已经存在 SSH 密钥对,如果没有则创建一个 if [ ! -f ~/.ssh/id_rsa ]; thenssh-keygen -t rsa -b 4096 -f ~/.ssh/id_rsa -N fi# 为每个目标主机复制公钥 for ip in 192.168.9.{11..16}; dossh-copy-id -i ~/.ssh/id_rsa.pub …...

CTFshow web93-104关
这周要学习的是php代码审计 根据师兄的作业 来做web入门的93-104关 93关 看代码 进行分析 他的主函数 include("flag.php"); highlight_file(__FILE__); if(isset($_GET[num])){ $num $_GET[num]; if($num4476){ die("no no no!"); …...
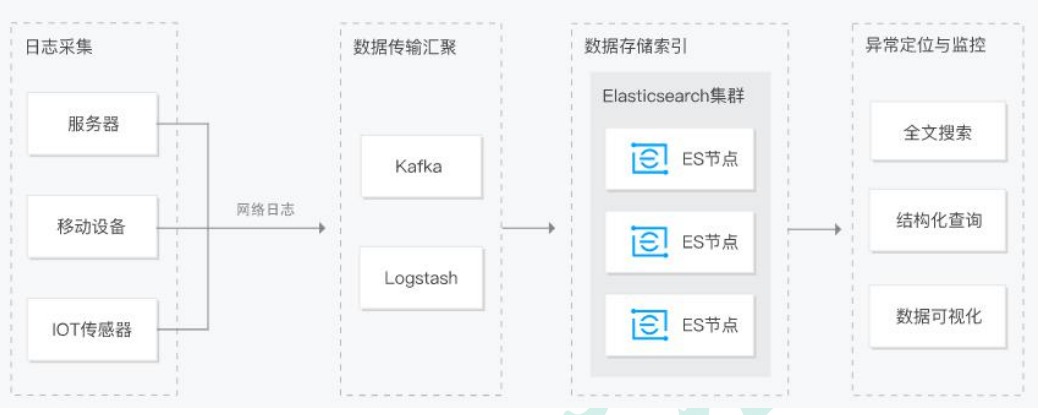
ElasticSearch详细操作
ElasticSearch搜索引擎详细操作以及概念 文章目录 ElasticSearch搜索引擎详细操作以及概念 1、_cat节点操作1.1、GET/_cat/nodes:查看所有节点1.2、GET/_cat/health:查看es健康状况1.3_、_GET/_cat/master:查看主节点1.4、GET/_cat/indices&a…...
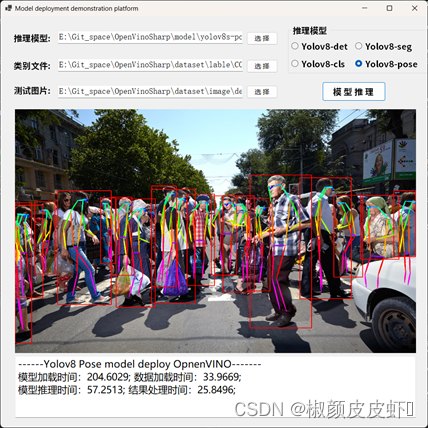
【OpenVINOSharp】 基于C#和OpenVINO2023.0部署Yolov8全系列模型
基于C#和OpenVINO2023.0部署Yolov8全系列模型 1 项目简介1.1 OpenVINOTM 2 OpenVinoSharp2.1 OpenVINOTM 2023.0安装配置2.2 C 动态链接库2.3 C#构建Core推理类2.4 NuGet安装OpenVinoSharp 3 获取和转换Yolov8模型3.1 安装ultralytics3.2 导出yolov8模型3.3 安装OpenVINOTM Pyt…...

121. 买卖股票的最佳时机
题目描述 给定一个数组 prices ,它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。 你只能选择 某一天 买入这只股票,并选择在 未来的某一个不同的日子 卖出该股票。设计一个算法来计算你所能获取的最大利润。 返回你可以从这笔交易中获取的…...
 LTO(Link-Time Optimization))
FDO(Feedback-Driven Optimization) LTO(Link-Time Optimization)
反馈驱动优化(Feedback-Driven Optimization,FDO)和链接时优化(Link-Time Optimization,LTO)是两种重要的编译器优化技术。下面我们详细介绍这两种技术: 反馈驱动优化 (FDO): FDO 是…...

低成本无刷高速吹风机单片机方案
高速吹风机的转速一般是普通吹风机的5倍左右。一般来说,吹风机的电机转速一般为2-3万转/分钟,而高速吹风机的电机转速一般为10万转/分钟左右。高转速增加了高风速。一般来说,吹风机的风力只有12-17米/秒,而高速吹风机的风力可以达…...

使用Python爬取某查查APP端(Appium自动化篇)
1. 写在前面 某查查网站反爬虫风控还是较强的,之后会分别介绍一下PC端协议、APP端自动化、APP端接口协议三种采集方案。这里主要介绍APP端的自动化方式,APP端自动化方式需要登陆账号,协议的话需要签名授权(自动化经测试没有太多限…...

vue3实现组件可拖拽 vuedraggable
npm i -S vuedraggablenext 中文文档,里面有完整代码案例,值得一看 vue.draggable vue3 版本在工作台中的应用场景 - itxst.com...

gradio常用组件
gradio常用组件 1.gradio程序启动2.写入html相关代码3.文本框4. 回车触发事件5.选择按钮框6.下拉框7.点击按钮8.清空按钮9.监听组件10.输出流11.template 1.gradio程序启动 import gradio as gr def tab():pass with gr.Blocks() as ui:gr.Markdown("# <center>&am…...

观成科技:隐蔽隧道工具Ligolo-ng加密流量分析
1.工具介绍 Ligolo-ng是一款由go编写的高效隧道工具,该工具基于TUN接口实现其功能,利用反向TCP/TLS连接建立一条隐蔽的通信信道,支持使用Let’s Encrypt自动生成证书。Ligolo-ng的通信隐蔽性体现在其支持多种连接方式,适应复杂网…...

【WiFi帧结构】
文章目录 帧结构MAC头部管理帧 帧结构 Wi-Fi的帧分为三部分组成:MAC头部frame bodyFCS,其中MAC是固定格式的,frame body是可变长度。 MAC头部有frame control,duration,address1,address2,addre…...

HBuilderX安装(uni-app和小程序开发)
下载HBuilderX 访问官方网站:https://www.dcloud.io/hbuilderx.html 根据您的操作系统选择合适版本: Windows版(推荐下载标准版) Windows系统安装步骤 运行安装程序: 双击下载的.exe安装文件 如果出现安全提示&…...

《C++ 模板》
目录 函数模板 类模板 非类型模板参数 模板特化 函数模板特化 类模板的特化 模板,就像一个模具,里面可以将不同类型的材料做成一个形状,其分为函数模板和类模板。 函数模板 函数模板可以简化函数重载的代码。格式:templa…...

【JVM】Java虚拟机(二)——垃圾回收
目录 一、如何判断对象可以回收 (一)引用计数法 (二)可达性分析算法 二、垃圾回收算法 (一)标记清除 (二)标记整理 (三)复制 (四ÿ…...

打手机检测算法AI智能分析网关V4守护公共/工业/医疗等多场景安全应用
一、方案背景 在现代生产与生活场景中,如工厂高危作业区、医院手术室、公共场景等,人员违规打手机的行为潜藏着巨大风险。传统依靠人工巡查的监管方式,存在效率低、覆盖面不足、判断主观性强等问题,难以满足对人员打手机行为精…...

Unity UGUI Button事件流程
场景结构 测试代码 public class TestBtn : MonoBehaviour {void Start(){var btn GetComponent<Button>();btn.onClick.AddListener(OnClick);}private void OnClick(){Debug.Log("666");}}当添加事件时 // 实例化一个ButtonClickedEvent的事件 [Formerl…...

stm32wle5 lpuart DMA数据不接收
配置波特率9600时,需要使用外部低速晶振...

第一篇:Liunx环境下搭建PaddlePaddle 3.0基础环境(Liunx Centos8.5安装Python3.10+pip3.10)
第一篇:Liunx环境下搭建PaddlePaddle 3.0基础环境(Liunx Centos8.5安装Python3.10pip3.10) 一:前言二:安装编译依赖二:安装Python3.10三:安装PIP3.10四:安装Paddlepaddle基础框架4.1…...

相关类相关的可视化图像总结
目录 一、散点图 二、气泡图 三、相关图 四、热力图 五、二维密度图 六、多模态二维密度图 七、雷达图 八、桑基图 九、总结 一、散点图 特点 通过点的位置展示两个连续变量之间的关系,可直观判断线性相关、非线性相关或无相关关系,点的分布密…...
