C++ 计算 拟合优度R^2
解决的问题:
拟合优度(Goodness of Fit)是指回归直线对观测值的拟合程度,度量拟合优度的统计量是可决系数(亦称确定系数) R?。R最大值为
1。R%的值越接近1,说明回归直线对观测值的拟合程度越好,反之,R%值越小,说明回归直线对观测值的拟合程度越差.
这是网上的介绍,那么根据算法的公式
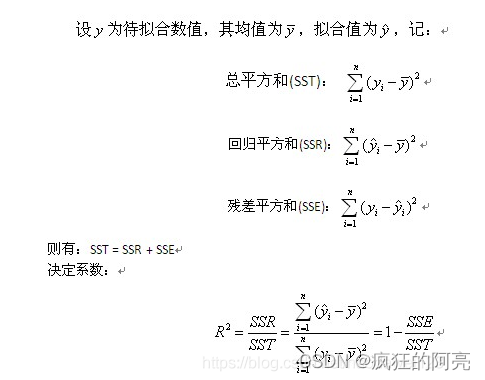
咱们实现自己的算法
如何实现:
1:拟合出自己的曲线方程式
y = a0 + a1*x + a2*x^2;
如下图:
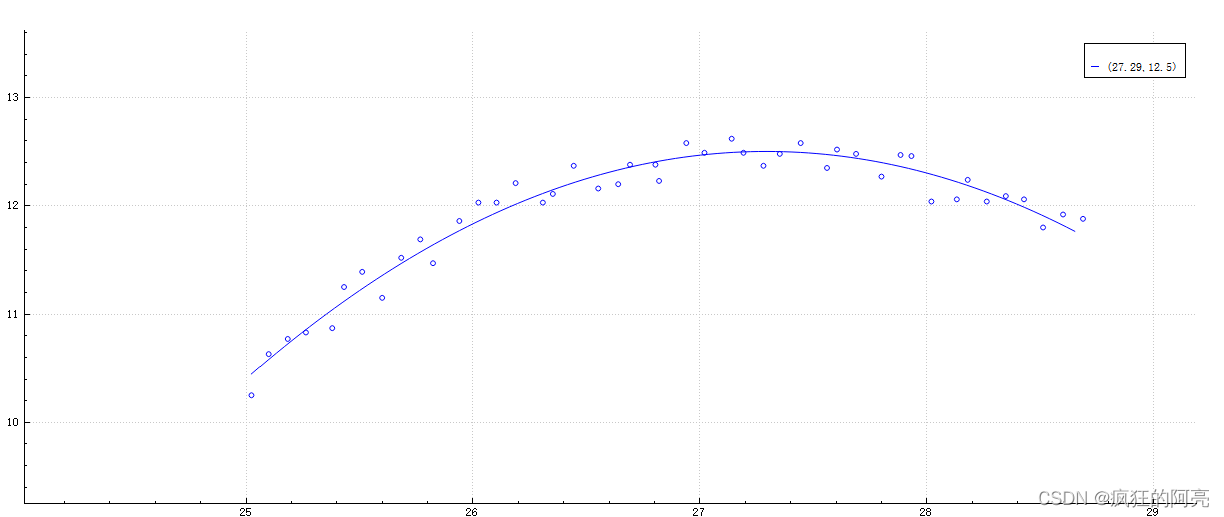
具体这个函数的拟合方法,有相应的代码,可以点关注私信我,我使用opencv自带的函数
cv::solve
然后就是计算R Squared的值
代码块解析:
double calculateMean(QVector<double> &numbers)
{double sum = 0.0;int count = 0.0;for (double number : numbers){sum += number;++count;}// 返回平均值return sum / count;
}double calculateYValue(double xValue)
{double yValue = 0.0;yValue = a0 + (a1 * xValue) + (a2*xValue*xValue);return yValue;
}double calculateRfitValue(QVector<double> x, QVector<double> y)
{double yMean = calculateMean(y);double SSR = 0.0;double SSE = 0.0;double SST = 0.0;for(int i = 0; i < x.length(); ++i){SSR += pow((calculateYValue(x[i]) - yMean), 2);SSE += pow((y[i] - calculateYValue(x[i])), 2);}SST = SSR + SSE;return (1.0- SSE/SST);
}int main(int argc, char *argv[])
{QCoreApplication a(argc, argv);QVector<double> myX = {29.82,29.62,29.42,29.21,29.01,28.8,28.59,28.38,28.17,27.97,27.76,27.55,27.34,27.13,26.92,26.71,26.5,26.3,26.09,25.88};QVector<double> myY = {133.2,135.2,137.12,139.2,141.2,142.3,143.5,144.2,144.9,145.3,143.6,145.8,144.6,143.4,142.0,140.2,138.7,136.2,133.7,130.4};qDebug() << "r2: " << calculateRfitValue(myX, myY);return a.exec();
}相关文章:

C++ 计算 拟合优度R^2
解决的问题: 拟合优度(Goodness of Fit)是指回归直线对观测值的拟合程度,度量拟合优度的统计量是可决系数(亦称确定系数) R?。R最大值为 1。R%的值越接近1,说明回归直线对观测值的拟合程度越好,反之,R%值越小&#x…...
Springboot-Retrofit HTTP工具框架快速使用
在SpringBoot项目直接使用okhttp、httpClient或者RestTemplate发起HTTP请求,既繁琐又不方便统一管理。 因此,在这里推荐一个适用于SpringBoot项目的轻量级HTTP客户端框架retrofit-spring-boot-starter,使用非常简单方便,同时又提供…...
)
微信小程序实现人脸识别(从一个没有开通人脸核身的小程序跳转到要给开通人脸核身的小程序,进行人脸识别后再跳转回来)
A小程序没有开通人脸识别功能,B小程序开通了人脸识别。 总体思路是:从A小程序需要进行人脸识别的地方携带参数跳转到B小程序进行人脸识别,识别后把参数传递回来。 A小程序的参考代码如下: //人脸识别相关 start powerDrawerFace(e){var that = thisthat.setData({faceO…...
CSS-grid布局
网格布局也叫grid布局,平常写样式的时候基本上都是用的flex布局。 像以下布局,用flex布局就可能会有有点麻烦,这时候用grid布局就方便的多了。 或者是照片墙 grid布局就是将容器划分为行和列,产生单元格,然后在指定的…...
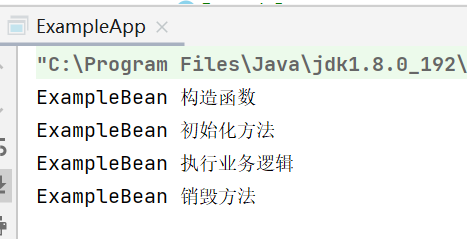
【JavaEE进阶】Bean 作用域和生命周期
文章目录 一. 关于Bean作用域的实例1. lombok2. 实例代码 二. 作用域定义1. Bean的六种作用域2. 设置作用域 三. Spring 执行流程和 Bean 的生命周期1. Spring 执行流程2. Bean生命周期 一. 关于Bean作用域的实例 注意在此例子中需要用到lombok 1. lombok lombok是什么? Lo…...
3分钟自建查分系统?现在每个人都可以实现了
学生成绩查询系统在现代教育管理中扮演着重要的角色,它不仅可以方便学生和家长查询成绩,也能帮助老师更好地管理和分析学生的学业表现。作为一名教师,了解如何制作学生成绩查询系统是提高教学效率和管理学生成绩便利性的关键。 在制作学生成…...

关于APP备案、小程序备案的问题,如何备案?
近日,工信部发布了关于开展移动互联网应用程序备案工作的通知。为落实相关法律法规要求,促进互联网行业规范健康发展,进一步做好移动互联网信息服务管理,现组织开展移动互联网应用程序(以下简称 APP)备案工…...

git上传代码后,如何清空历史日志以及文件操作,重新上传?以及上传代码
【Git教程】如何清除git仓库的所有提交记录,成为一个新的干净仓库 马三也算Github的忠实用户了,经常会把一些练手的项目传到Github上面进行备份。其中有一个名为ColaFramework的Unity框架项目,马三开发了一年多了,期间提交代码的…...

超导热催生meme,换汤不换药的投机轮回
文/章鱼哥 出品/陀螺财经 币圈对炒作meme概念的热情从未消亡过。 随着一种名为LK-99的物质被发现,围绕超导的兴奋不仅激发了科学界,加密货币相关概念也与之沸腾。不出所料,与此前围绕元宇宙、AI大肆炒作一样,许多meme代币已经出现…...

【HashMap】 73. 矩阵置零
73. 矩阵置零 解题思路 首先遍历矩阵找到所有的0元素 将其的行和列索引记录下俩遍历矩阵 将所有的需要更新的元素进行更新 也就是查找hashmap中的每一个元素进行更新查找行或者列是否在hashmap中 class Solution {public void setZeroes(int[][] matrix) {// 首先遍历矩阵找…...
Vue-2.nodejs的介绍和安装
nodejs简介 ► 创建 Node.js 应用:package.json 首先,创建一个新文件夹以便于容纳需要的所有文件,并且在此其中创建一个 package.json 文件,描述你应用程序以及需要的依赖: 配合着你的 package.json 请运行 npm install。如果你…...

分别用Vue和Java来实现的风靡一时的2048 游戏
目录 1、Vue实现2、Java实现 2048 游戏是一个基于网格的数字益智游戏,玩家需要通过滑动相同的数字来合并它们,并最终得到一个值为 2048 的方块。以下是分别用Vue和Java来实现的 2048 游戏,包含运行效果。 1、Vue实现 首先,创建一…...
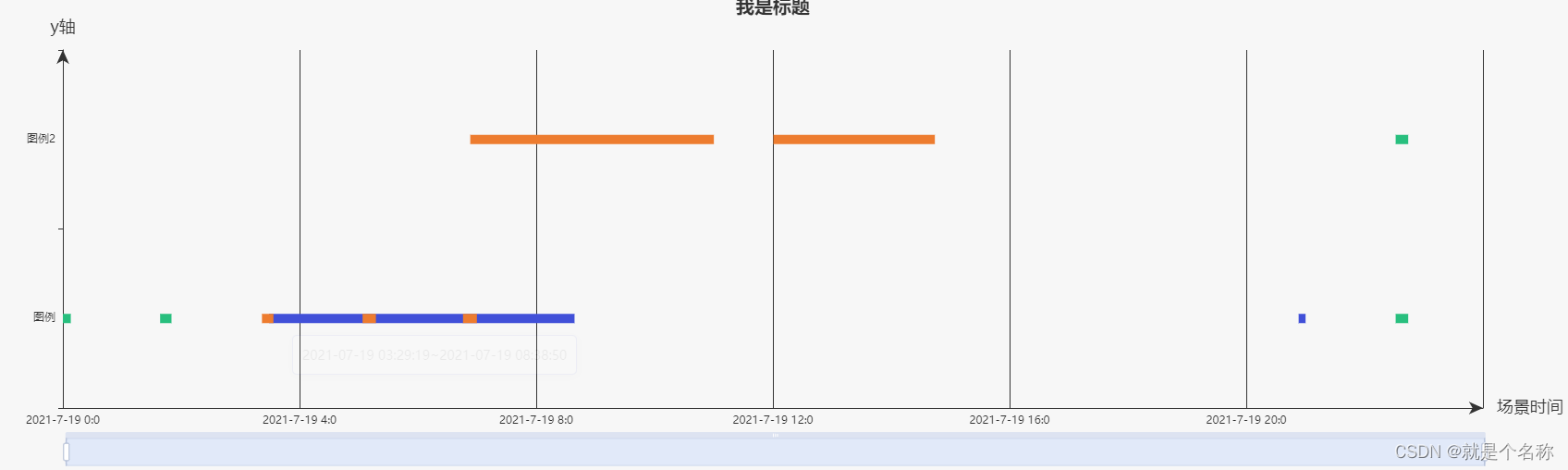
echarts甘特图 一个值多条线
先看图 这里我们用到的是 series :type:custom 自定义,但是这里我遇到一个问题,就是不过你在series里push多少数据,图表上显示的都是在同一水平线,用了好多方法都不好使, renderItem: (params, api) >…...

多态性说明
多态 多态性多态性类型描述编译时多态和运行时多态的差异go 语言多态性 多态性 多态性类型描述 多态性是面向对象编程中的一个重要概念,它允许不同的对象通过相同的接口表现出不同的行为,从而实现更加灵活和可扩展的代码结构。多态性有助于降低代码的耦…...

2023-08-04 LeetCode每日一题(不同路径 III)
2023-08-04每日一题 一、题目编号 980. 不同路径 III二、题目链接 点击跳转到题目位置 三、题目描述 在二维网格 grid 上,有 4 种类型的方格: 1 表示起始方格。且只有一个起始方格。2 表示结束方格,且只有一个结束方格。0 表示我们可以…...

腾讯云服务器地域怎么选?可用区是什么?
腾讯云服务器地域有什么区别?怎么选择比较好?地域选择就近原则,距离地域越近网络延迟越低,速度越快。关于地域的选择还有很多因素,地域节点选择还要考虑到网络延迟速度方面、内网连接、是否需要备案、不同地域价格因素…...
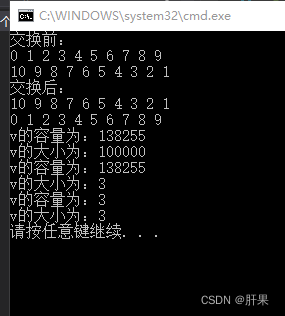
第一百二十三天学习记录:C++提高:STL-vector容器(下)(黑马教学视频)
vector插入和删除 功能描述: 对vector容器进行插入、删除操作 函数原型: push_back(ele); //尾部插入元素ele pop_back(); //删除最后一个元素 insert(const_iterator pos, ele); //迭代器指向位置pos插入元素ele insert(const_iterator pos, int cou…...

谈谈Spring与字节码生成技术
Spring框架是一个面向企业级Java应用开发的开源框架,它提供了许多功能和特性来简化Java开发过程。字节码生成技术在Spring框架中起着重要的作用,用于实现依赖注入(Dependency Injection)和面向切面编程(Aspect-Oriente…...

Java数组详解 -- 基础知识与常用操作
文章目录 前言一、初识数组1. 数组的定义2. 数组的特点3. 声明和初始化数组4. 默认初始化值 二、访问和操作数组元素1. 数组的索引和范围2. 通过索引访问数组元素3. 修改数组元素的值 三、数组的长度和属性1. 数组的长度计算2. 数组的长度属性3. 数组越界的错误 四、数组的遍历…...
第五章 决策树——一二三节:决策树模型与学习,特征选择,决策树的生成,)
(统计学习方法|李航)第五章 决策树——一二三节:决策树模型与学习,特征选择,决策树的生成,
目录 一,决策树模型与学习 1.决策数模型 2.决策树与if-then规则 3.决策树与条件概率分布 4.决策树学习 二,特征选择 1.特征选择问题 2.信息增益 3.信息增益比 三,决策树的生成 1.ID3算法 2.C4.5的生成算法 一,决策树模型…...

Cursor实现用excel数据填充word模版的方法
cursor主页:https://www.cursor.com/ 任务目标:把excel格式的数据里的单元格,按照某一个固定模版填充到word中 文章目录 注意事项逐步生成程序1. 确定格式2. 调试程序 注意事项 直接给一个excel文件和最终呈现的word文件的示例,…...
:OpenBCI_GUI:从环境搭建到数据可视化(下))
脑机新手指南(八):OpenBCI_GUI:从环境搭建到数据可视化(下)
一、数据处理与分析实战 (一)实时滤波与参数调整 基础滤波操作 60Hz 工频滤波:勾选界面右侧 “60Hz” 复选框,可有效抑制电网干扰(适用于北美地区,欧洲用户可调整为 50Hz)。 平滑处理&…...

MySQL 隔离级别:脏读、幻读及不可重复读的原理与示例
一、MySQL 隔离级别 MySQL 提供了四种隔离级别,用于控制事务之间的并发访问以及数据的可见性,不同隔离级别对脏读、幻读、不可重复读这几种并发数据问题有着不同的处理方式,具体如下: 隔离级别脏读不可重复读幻读性能特点及锁机制读未提交(READ UNCOMMITTED)允许出现允许…...

遍历 Map 类型集合的方法汇总
1 方法一 先用方法 keySet() 获取集合中的所有键。再通过 gey(key) 方法用对应键获取值 import java.util.HashMap; import java.util.Set;public class Test {public static void main(String[] args) {HashMap hashMap new HashMap();hashMap.put("语文",99);has…...

iPhone密码忘记了办?iPhoneUnlocker,iPhone解锁工具Aiseesoft iPhone Unlocker 高级注册版分享
平时用 iPhone 的时候,难免会碰到解锁的麻烦事。比如密码忘了、人脸识别 / 指纹识别突然不灵,或者买了二手 iPhone 却被原来的 iCloud 账号锁住,这时候就需要靠谱的解锁工具来帮忙了。Aiseesoft iPhone Unlocker 就是专门解决这些问题的软件&…...

在 Nginx Stream 层“改写”MQTT ngx_stream_mqtt_filter_module
1、为什么要修改 CONNECT 报文? 多租户隔离:自动为接入设备追加租户前缀,后端按 ClientID 拆分队列。零代码鉴权:将入站用户名替换为 OAuth Access-Token,后端 Broker 统一校验。灰度发布:根据 IP/地理位写…...

2025 后端自学UNIAPP【项目实战:旅游项目】6、我的收藏页面
代码框架视图 1、先添加一个获取收藏景点的列表请求 【在文件my_api.js文件中添加】 // 引入公共的请求封装 import http from ./my_http.js// 登录接口(适配服务端返回 Token) export const login async (code, avatar) > {const res await http…...

第一篇:Agent2Agent (A2A) 协议——协作式人工智能的黎明
AI 领域的快速发展正在催生一个新时代,智能代理(agents)不再是孤立的个体,而是能够像一个数字团队一样协作。然而,当前 AI 生态系统的碎片化阻碍了这一愿景的实现,导致了“AI 巴别塔问题”——不同代理之间…...

SpringCloudGateway 自定义局部过滤器
场景: 将所有请求转化为同一路径请求(方便穿网配置)在请求头内标识原来路径,然后在将请求分发给不同服务 AllToOneGatewayFilterFactory import lombok.Getter; import lombok.Setter; import lombok.extern.slf4j.Slf4j; impor…...

智能仓储的未来:自动化、AI与数据分析如何重塑物流中心
当仓库学会“思考”,物流的终极形态正在诞生 想象这样的场景: 凌晨3点,某物流中心灯火通明却空无一人。AGV机器人集群根据实时订单动态规划路径;AI视觉系统在0.1秒内扫描包裹信息;数字孪生平台正模拟次日峰值流量压力…...
