python机器学习(六)决策树(上) 构造树、信息熵的分类和度量、信息增益、CART算法、剪枝
决策树算法
模拟相亲的过程,通过相亲决策图,男的去相亲,会先选择性别为女的,然后依次根据年龄、长相、收入、职业等信息对相亲的另一方有所了解。
通过决策图可以发现,生活中面临各种各样的选择,基于我们的经验和自身需求进行一些筛选,把判断背后的逻辑整理成结构图,会发现呈现树状的结构,也就是所说的树状图。
我们在做决策的时候,会经历两个阶段:构造和剪枝。
构造树
构造就是生成一颗完整的决策树,简单来说,构造的过程就是选择什么属性作为节点的过程,那么在构造过程中,会存在三种节点:
- 根节点:位置位于树的最顶端,可以最大化的去划分类别,帮助我们筛选数据
- 内部节点:位于树中间的节点,也为子节点。
- 叶节点:每个节点决策的结果,不存在子节点。
所以在构造树的过程中,我们要解决三个重要的问题:
- 选择哪个属性作为根节点
- 选择哪些属性作为内部节点(子节点)
- 什么时候停止并且得到目标状态(叶节点)
根节点选择的不同会导致树的选择也存在差异。
问题: 我们怎么来用程序选择根节点呢
目标:通过一种衡量标准,来计算通过不同特征进行分支选择后的分类情况,找出来最好的那个当成根节点,依次类推。
利用根节点可以更好的去切分数据,内部节点是为了更好的细分数据。
信息熵(Entropy)
信息熵是表示随机变量不确定性的度量。熵是物理学中的知识点,表示物体内部的混乱程度,比如口红种类色号繁多,意味着在商场中轻松买到一支完全满意的口红的概率非常低,说明当种类比较混乱的话,不确定性就越大,熵值也就越大;比如要买华为的手机,进入华为专卖店就可以购买,确定性越大,意味着熵值就越小。
熵与分类的关系
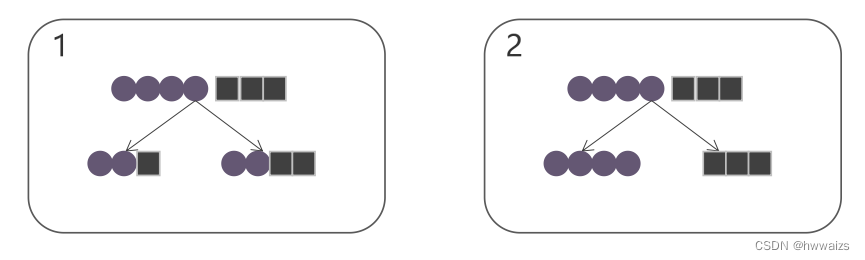
1图进行分类后更混乱了,混乱程度越大,不确定性越大,熵值就越大,2图分类后数据比较纯,分类明确规整,熵值就越小。
用程序去实现的话,就要把指标进行量化。
信息熵的度量
单位:1bit
一枚硬币有正反两面,抛硬币出现反面的概率是50%,出现证明的概率也是50%,这是最简单的二分类的问题,抛一个硬币的不确定性记为1bit,抛硬币的个数,与它呈现的不确定的结果是指数的关系。
1枚硬币:不确定性为2,正反
2枚硬币:不确定性为4,全正,全反,一正一反,一反一正
3枚硬币:不确定性为8
n枚硬币:不确定性为2^n
等概率均匀分布
4种不确定结果 = 2 2 2^2 22,熵为2bit, 2 = l o g 2 4 2=log_24 2=log24
8种不确定结果 = 2 3 2^3 23,熵为3bit, 3 = l o g 2 8 3=log_28 3=log28
m种不确定结果 = 2 n 2^n 2n,熵为nbit, n = l o g 2 m n=log_2m n=log2m
概率都是相等的情况, n = l o g 2 m n=log_2m n=log2m,m为不确定性结果的个数。
概率不等分布
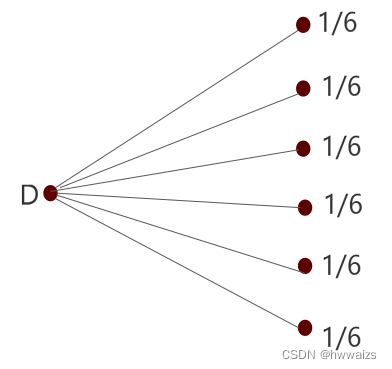
把 D D D分为6种情况,不确定性结果为6,也即为 m = 6 m=6 m=6, D D D的熵为: E n t ( D ) = l o g 2 6 Ent(D)=log_26 Ent(D)=log26
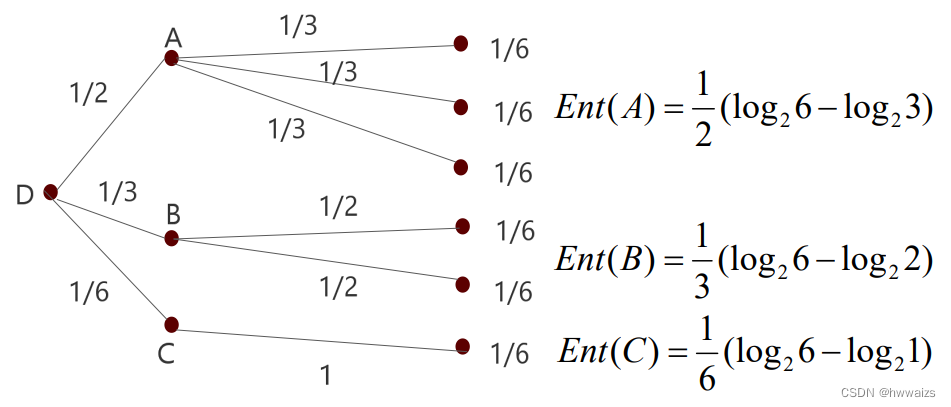
真实的情况可能更加复杂,如下图, D D D的不确定性分为 A 、 B 、 C A、B、C A、B、C三种, A A A又有三种情况为1/2的概率, B B B有两种情况为1/3的概率, C C C有一种情况为1/6的概率。 A A A有三种可能,对应的m(A)=3,单个A的熵为 l o g 2 3 log_23 log23, D D D的数据更纯,纯度高的减去纯度低的得到数据本身的纯度,再考虑概率的问题,乘以权重。
A A A处的熵为 E n t ( A ) = 1 2 ( l o g 2 6 − l o g 2 3 ) Ent(A)=\frac{1}{2}(log_26-log_23) Ent(A)=21(log26−log23)。
B 、 C B、C B、C的熵依此类推。
E n t ( B ) = 1 3 ( l o g 2 6 − l o g 2 2 ) Ent(B)=\frac{1}{3}(log_26-log_22) Ent(B)=31(log26−log22)
E n t ( C ) = 1 6 ( l o g 2 6 − l o g 2 1 ) Ent(C)=\frac{1}{6}(log_26-log_21) Ent(C)=61(log26−log21)
D D D的熵为: E n t ( D ) = E n t ( A ) + E n t ( B ) + E n t ( C ) Ent(D)=Ent(A)+Ent(B)+Ent(C) Ent(D)=Ent(A)+Ent(B)+Ent(C),推导之后可得:
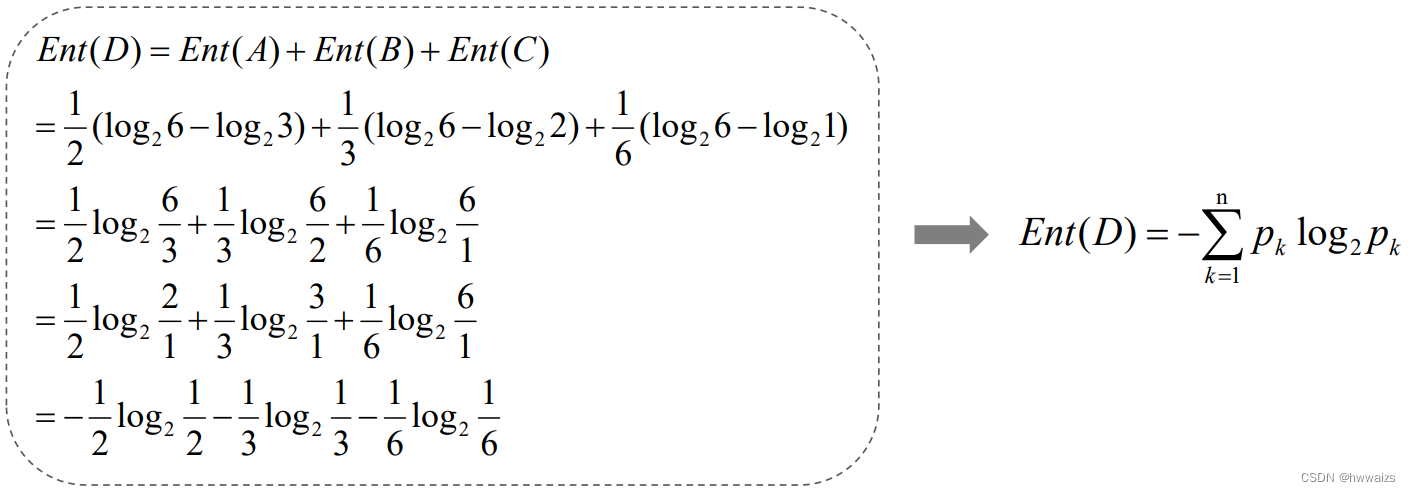
下图为对数的图形,必要过点 ( 1 , 0 ) (1,0) (1,0),横坐标为 P k P_k Pk,纵坐标为 E n t ( A ) Ent(A) Ent(A), P k = 1 P_k=1 Pk=1的时候意味着概率为1,熵为0,表示数据纯度最高。 P k = 1 P_k=1 Pk=1的作用域为0到1之间,所以图形中大于1的部分是没有的。
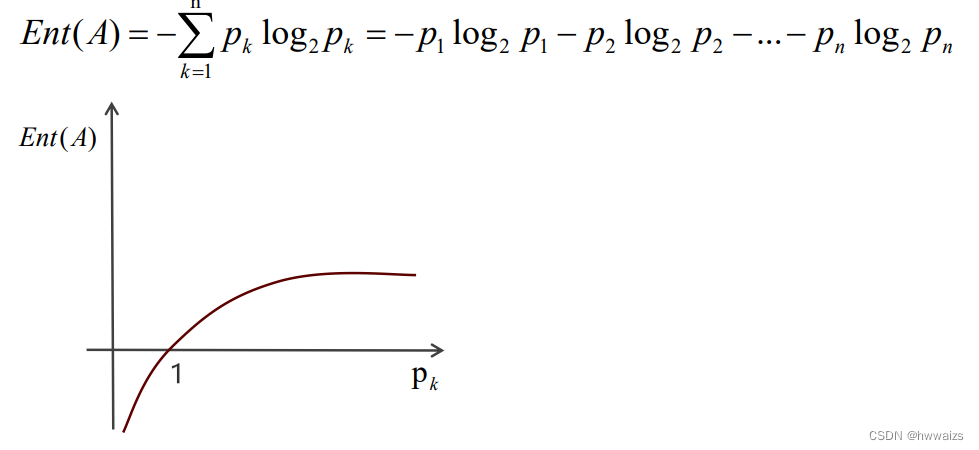
也就是说概率越大,混乱程度越低,熵值就越低。
- 练习1
下图中,图2的熵值大,混乱程度高,图1数据比较纯,都是圆圈,不确定性小,熵值就越小。

- 练习2
集合A:[1,2,3,4,5,6,7,8,9,10]
集合B:[1,1,1,1,1,1,1,1,9,10]
集合B的熵值小,B的数据相对比较纯,出现1的概率比较大,熵值小,稳定性比较高。
做决策树的时候,熵值越低表示数据越纯,分类的效果就会更明显,在数模型中,希望熵值越来越小,
信息增益
熵可以表示样本集合的不确定性,熵越大,样本的不确定性就越大。因此可以使用划分前后集合熵的差值来衡量使用当前特征对于样本集合Y划分结果的好坏。
信息增益表示特征X使得类Y的不确定性减少的程度,决策一个节点的选择。
下图中根节点Y的熵数据比较大为0.9,数据比较混乱,现对Y划分为Y_1和Y_2,熵分布为0.2和0.5,可以看出Y_1的分类效果比较明显。 0.9 − 0.2 > 0.9 − 0.5 0.9-0.2>0.9-0.5 0.9−0.2>0.9−0.5
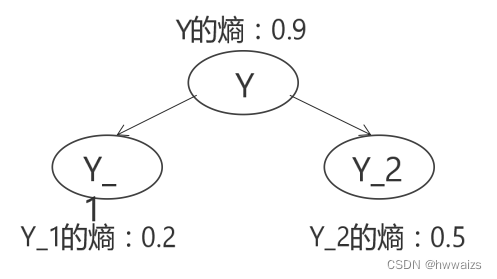
特征A对训练数据集D的信息增益 g ( D , A ) g(D,A) g(D,A),定义为集合 D D D的信息熵 H ( D ) H(D) H(D)与特征 A A A给定条件下 D D D的信息条件熵 H ( D ∣ A ) H(D|A) H(D∣A)之差。即公式为: g ( D , A ) = H ( D ) − H ( D ∣ A ) g(D,A)=H(D)-H(D|A) g(D,A)=H(D)−H(D∣A)
本质上为初始熵和信息熵的差距。
- 信息增益计算例题
如下图,我们根据天气、温度、湿度、刮风四个特征来判断是否打球。
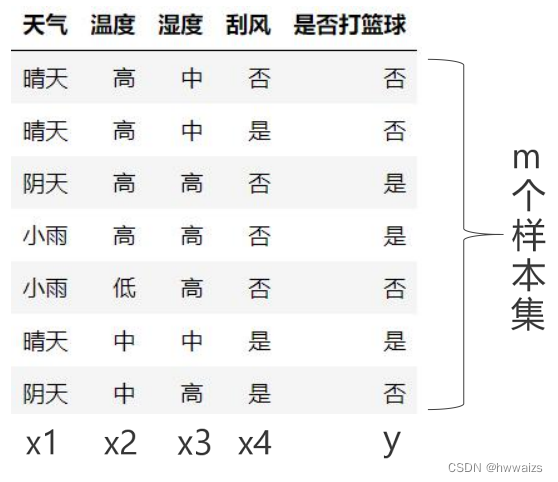
特征:天气、温度、湿度、刮风
标签:是否打篮球
每个特征都决定着标签,对最终结果的影响如下图所示:
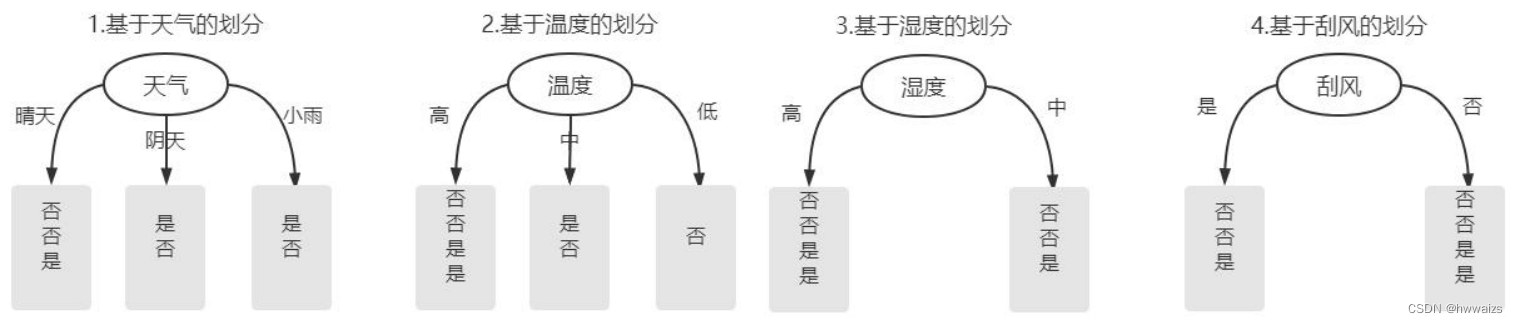
计算过程:
单单从数据上无法判断哪个特征作为根节点,要根据信息增益来选择作为根节点的特征,信息增益越大越好,增益越大说明划分的越有效果,从数据不纯往数据数据越纯的方向上移动。- 1.计算初始熵
- 2.计算各特征的熵
- 3.进行球差得到信息增益
- 4.选择信息增益大的特征作为根节点


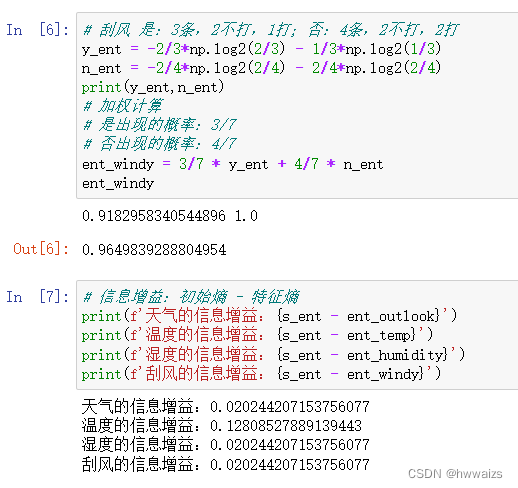
计算结果为温度的信息增益最大,选择温度作为根节点,再从湿度、天气、刮风中选择子节点构建完整的决策树。
通过信息增益获得决策树,是决策算法的一种,称为ID3算法。
ID3算法的缺陷
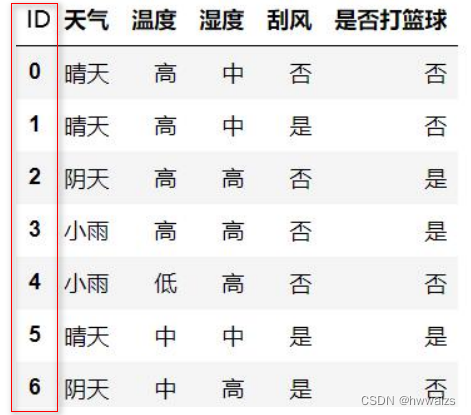
如果在刚才的表格上增加一列ID,ID列的每个数字都不一样,以ID特征来进行分类,每一个ID值不相等且均为单独的一类,每个类都只有自己,意味着数据比较纯,每个数据出现的概率都是100%,意味着ID为0,它的熵为0;ID为6,熵依然为0。如果使用信息增益的话,ID列被作为根节点,它跟最后的结果打球不打球没有关系。
所以ID3算法是由缺陷的,信息增益倾向于分类较多的特征,有些噪音数据就会影响整体的分类,甚至整个树的构造,为了解决这个缺陷,提出了信息增益率。
信息增益率(C4.5)
ID3在计算的时候,倾向于选择取值比较多的属性。为了避免这个问题,C4.5采用信息增益率的方式来选择属性。信息增益率 = 信息增益 / 属性熵,属性就是特征。熵代表数据的混乱程度,数据的不确定性。如果一个属性有多个值,数据就会被划分为多份,数据的概率变大了,虽然信息增益变大了,属性熵也会变大,整体的信息增益率就没有变的那么大。分成多份后,每个类别的熵变低了,对于整个样本来说,不确定性增强了,熵变大了,分类越多,信息增益就越大,信息熵也就变大了。信息增益和熵是同时同向变化的,所以二者的比值就会减少影响,二者成正比的关系,减少信息增益的变大。
CART算法
CART算法,英文全名为(Classification And Regression Tree),中文叫做分类回归树。ID3和C4.5算法可以生成二叉树或多叉树,而CART只支持二叉树。同时CART决策树比较特殊,既可以作分类树,又可以作回归树。
CART分类树与C4.5算法类似,只是在属性选择的衡量指标采用的是基尼系数,用的不再是信息增益或信息增益率。基尼系数是用来衡量一个国家收入差距的常用指标。基尼系数本身反映了样本的不确定度,当基尼系数越小的时候,说明样本之间的差异性小,不确定程度低。分类的过程本身就是提纯的过程,使用CART算法在构造分类树的时候,会选择基尼系数最小的作为属性的划分,跟熵是相反的。
GINI系数公式: G i n i ( D ) = 1 − ∑ k = 1 ∣ y ∣ P k 2 Gini(D)= 1-\displaystyle{\sum_{k=1}^{|y|}P_k^2} Gini(D)=1−k=1∑∣y∣Pk2
如果概率为1,数据的纯度越高,基尼系数就为0。二分类的问题,y不是0就为1,
基尼系数构建决策树:
- 计算初始基尼系数
- 分别计算各特征的基尼系数
- 做差计算基尼系数增益


通过计算得知,温度的基尼系数最大,可以选择作为根节点。
连续性数据处理实现
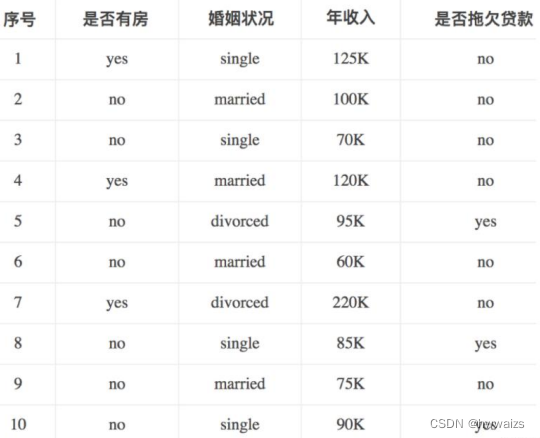
在实际过程中,我们有很多连续值,比如下图年收益就是连续的值,其实就是数值型的属性,那我们怎么来计算基尼系数呢?
流程如下:
- 将乱序的值进行从小到大排序
- 不断的二分

对数据两两数据取中间值,如60和70的中间值是65,70和75的中间值为72.5,依次类推。以65作为分割点,小于65的数只有1个,占数据的十分之一,剩下十分之九里面6个无贷款,3个有贷款计算出基尼增益为0.02;依次以72.5为分割点进行计算,得到上图中的Gini系数增益,得到基尼增益最好的点作为根节点。

连续性数据的处理过程是将连续值进行离散化的过程。
剪枝
剪枝就是给决策树瘦身,这一步想实现的目标就是,不需要太多的判断,同样可以得到不同的结果。比如梯度下降的时候进行了1万次,可能在几百次的时候已经出现了最好的结果,剪枝是为了防止“过拟合”(Overfitting)现象的发生,得到最好结果的时候就停止。过拟合训练集太过完美,测试集在测试的时候结果就会不是很满意。
需要使用剪枝防止过拟合的发生,如果不剪枝一直进行分裂,那样本数据100%会被分割到一个正确的结果。如下图所示,一直进行分裂。
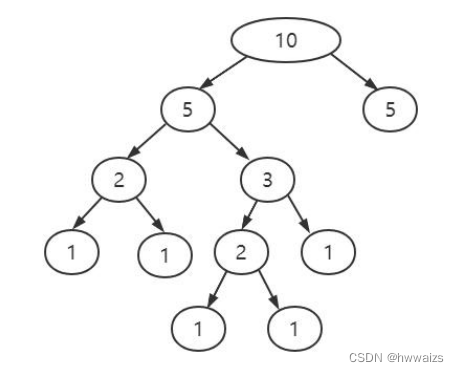
不停的分下去跟分到一半的效果是一样的,就没有必要一直往下分了,否则会一直占用计算机的资源。
预剪枝
在构造树枝前进行一些设定:
- 指定树的高度或者深度,比如上图对10进行分裂了4次,如果指定高度为3,则第4次就不会被执行
- 每一个结点所包含的最小样本数目,比如说指定最小样本数为3,则到3之后也不会往下执行了
- 指定结点的熵小于某个值,不再划分,比如指定熵为0.2,恰好2处的熵为0.2,则也不会往下执行了
后剪枝
在已生成过拟合决策树上进行剪枝,可以得到简化版的剪枝决策树。
相关文章:

python机器学习(六)决策树(上) 构造树、信息熵的分类和度量、信息增益、CART算法、剪枝
决策树算法 模拟相亲的过程,通过相亲决策图,男的去相亲,会先选择性别为女的,然后依次根据年龄、长相、收入、职业等信息对相亲的另一方有所了解。 通过决策图可以发现,生活中面临各种各样的选择,基于我们的…...
eNSP:ospf和mgre的配置
完成下图操作: 信息标注: 如下是各路由器上的命令: r1: <Huawei>sys Enter system view, return user view with CtrlZ. [Huawei]sys r1 [r1]int loop0 [r1-LoopBack0]ip add 192.168.1.1 24 [r1-LoopBack0]int g0/0/0 …...
培训报名小程序-订阅消息发送
目录 1 创建API2 获取模板参数3 编写自定义代码4 添加订单编号5 发送消息6 发布预览 我们上一篇讲解了小程序如何获取用户订阅消息授权,用户允许我们发送模板消息后,按照模板的参数要求,我们需要传入我们想要发送消息的内容给模板,…...

资深测试员才知道的五个行业秘密
作为一名资深测试员,总有一些平时难以诉说的行业秘密,我也不例外。也许这些秘密你认可,也许你嗤之以鼻,但不管如何,我都希望能给你带来一丝感悟,更深的认识测试,并走得更远。 1、手工测试不可替…...

Ozone命令行接口详解
命令行接口简介 Ozone Shell是命令行与Ozone交互的主要界面,底层用的是Java。 有些功能只能通过Ozone Shell进行操作: 创建带有限额限制的Volume管理内部ACLs(访问控制列表)创建带有加密密钥的存储桶 大部分操作除了Shell操作…...
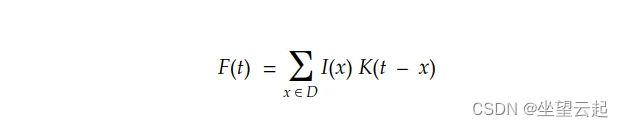
机器学习笔记 - 基于C++的深度学习 二、实现卷积运算
一、卷积 卷积是信号处理领域的老朋友。最初的定义如下 在机器学习术语中: I(…)通常称为输入 K(…)作为内核,并且 F(…)作为给定K的I(x)的特征图。 虑多维离散域,我们可以将积分转换为以下求和 对于二维数字图像,我们可以将其重写为: <...

python pandas 获取Excel文件下所有的sheet名称,表格数据
方法1: 一定要加sheet_nameNone,才能读取出所有的sheet,否则默认读取第一个sheet,且获取到的keys是第一行的值 df pd.read_excel(自己的Excel文件路径.xlsx, sheet_nameNone) # 路径注意转义 for i in df.keys():print(i)方法…...
gateway做token校验
本文使用springcloud的gateway做token校验 登录的本质:拿用户名和密码 换 token。 token会返回给浏览器(存储),当访问的时候,携带token 发起请求。 token校验图 引入redis依赖 <dependency><groupId>or…...

C#学习记录-线程
线程 定义:Thread t new Thread(Test); //可以用匿名 lamda 调用:t.Start("ljc6666");方法可以无参或一个参数,如果要传入多个参数,可以传入一个结构体 namespace _17_线程Thread {internal class Program{stati…...
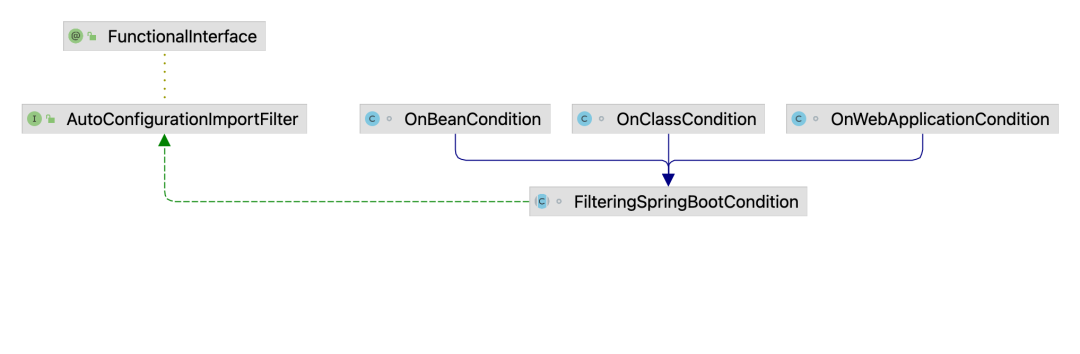
Spring Boot 启动注解分析
虽然我们在日常开发中,Spring Boot 使用非常多,算是目前 Java 开发领域一个标配了,但是小伙伴们仔细想想自己的面试经历,和 Spring Boot 相关的面试题都有哪些?个人感觉应该是比较少的,Spring Boot 本质上还…...

React Native数据存储
最近做RN开发中需要数据存储,查阅RN官方资料,发现推荐我们使用 AsyncStorage,对使用步骤做一下记录。 AsyncStorage是什么 简单的,异步的,持久化的key-value存储系统AsyncStorage在IOS下存储分为两种情况: 存储内容较…...

【网络编程】揭开套接字的神秘面纱
文章目录 1 :peach:简单理解TCP/UDP协议 :peach:2 :peach:网络字节序 :peach:3 :peach:socket编程接口 :peach:3.1 :apple:socket 常见API :apple:3.2 :apple:sockaddr结构:apple: 4 :peach:简单的UDP网络程序 :peach:4.1 :apple:基本分析:apple:4.2 :apple:udpServer.hpp(重点…...

MySQL 8.0 事务定义和基本操作
MySQL 事务(Transaction)的四大特性:A、C、I、D A、原子性:(Atomicity) 一个事务是不可分割的最小工作单位。 执行的事务,要么全部成功,要么回滚到执行事务之前的状态。 C、一致…...
项目经理必备:常用的项目管理系统推荐!
当我们成为项目负责人时,找到合适的工具来管理跟进项目,就成为了迫切需要解决的问题。一款优秀的工具,在项目的管理跟进中,起着极为重要的作用,一般可以付费购买专门的项目管理软件。 1.可快速切换查看不同角度的项目信…...
)
【香瓜说职场】信任危机(2022.08.19)
自从17年4月份开始辞职创业,已经5年零4个月了。今天跟大家聊一点不太正能量的事。 首先关于“要不要说些不好的”这件事,我爸妈常建议我不要把不好的事情写出来,因为觉得丢人、不体面、怕影响合伙人关系、影响同事关系。而我觉得如果只写好的…...
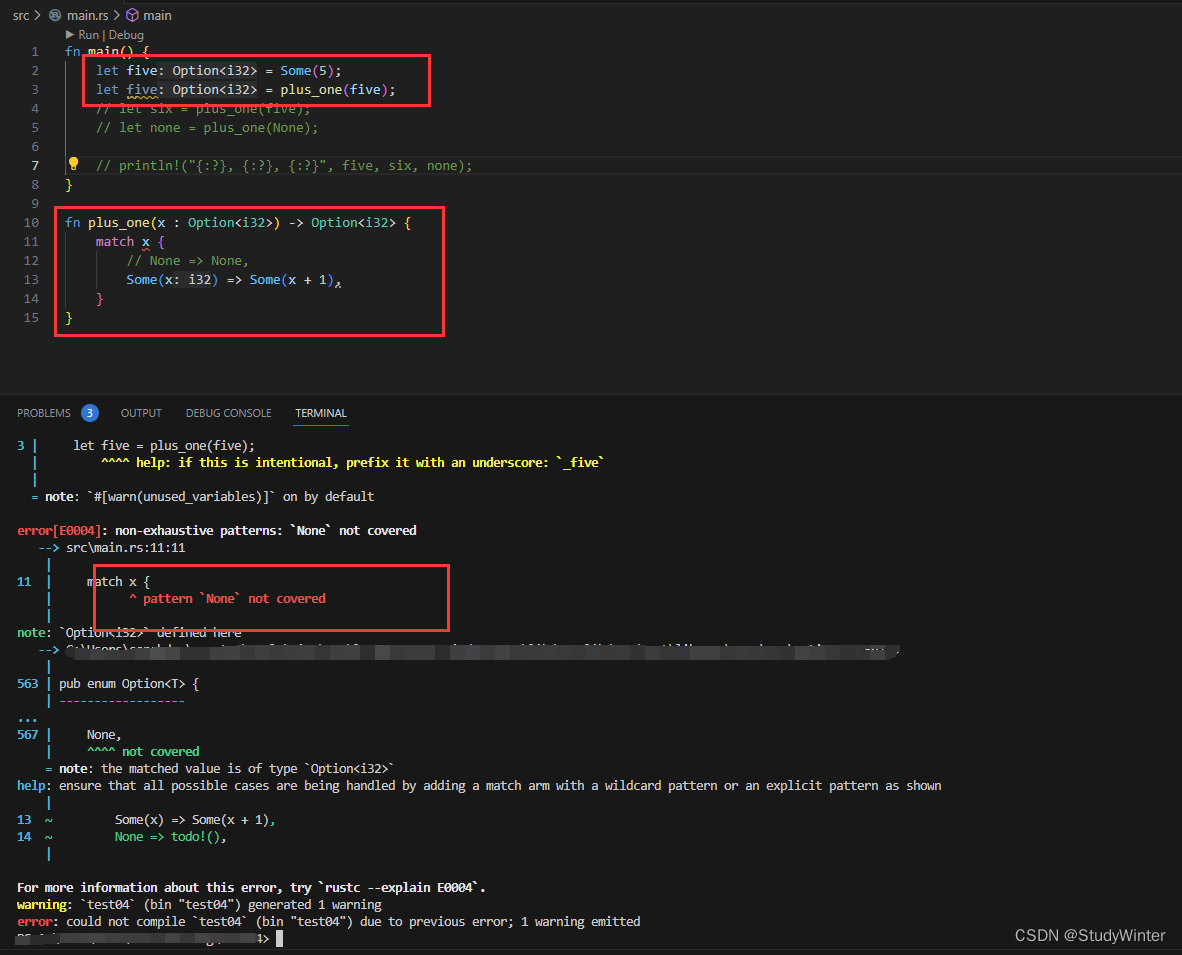
【Rust】Rust学习 第六章枚举和模式匹配
本章介绍 枚举(enumerations),也被称作 enums。枚举允许你通过列举可能的 成员(variants) 来定义一个类型。首先,我们会定义并使用一个枚举来展示它是如何连同数据一起编码信息的。接下来,我们会…...

Win10安装GPU支持的最新版本的tensorflow
我在安装好cuda和cudnn后,使用pip install tensorflow安装的tensorflow都提示不能找到GPU, 为此怀疑默认暗转的tensorflow是不带GPU支持的。 在tensorflow官网提供了多个版本的GPU支持的windows的安装包 https://www.tensorflow.org/install/pip?hlz…...

20个Golang自动化DevOps库
探索 20 个用于简化任务和提高生产力的重要库。 Golang,也称为 Go,是一种静态类型、编译型编程语言,由 Google 的 Robert Griesemer、Rob Pike 和 Ken Thompson 设计。它于 2009 年推出,旨在解决其他编程语言的缺点,特…...
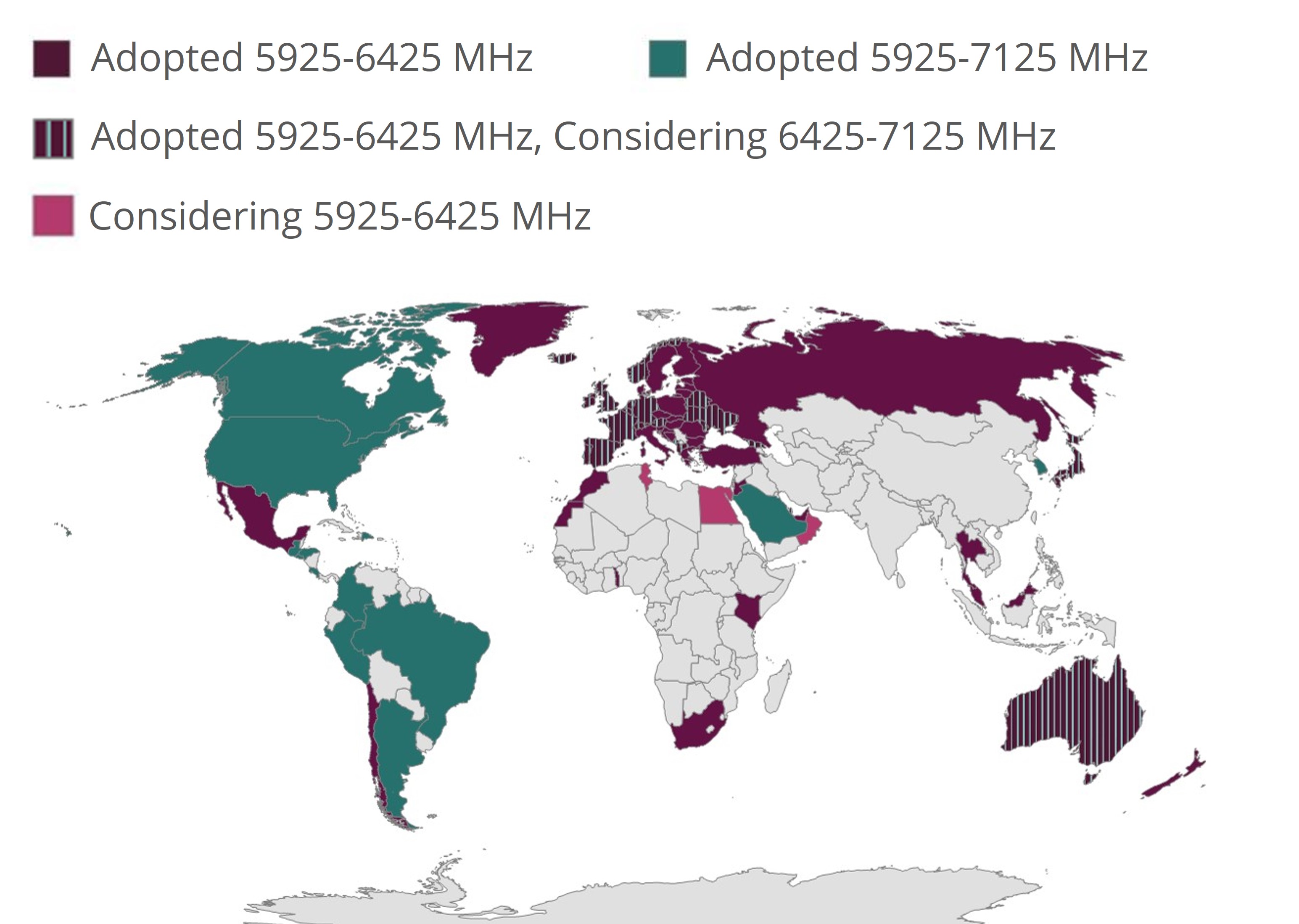
【WiFi】WiFi 6E最新支持的国家和频段
信道Map图 国家和频段 CountryStatus Spectrum Andorra Adopted Considering 5945-6425 MHz 6425-7125 MHz ArgentinaAdopted5925-7125 MHzAustralia Adopted Considering 5925-6425 MHz 6425-7125 MHz Austria Adopted Considering 5945-6425 MHz 6425-7125 MHz BahrainA…...

如何使用html,包括css,js 画思维导图?有哪些可用的方法?
首先,创建一个新的HTML文件,可以使用任何文本编辑器。在文件中添加必要的标签和结构来定义网页的内容和布局。 <!DOCTYPE html> <html> <head><meta charset"UTF-8"><title>Mind Map</title><link re…...

【SQL学习笔记1】增删改查+多表连接全解析(内附SQL免费在线练习工具)
可以使用Sqliteviz这个网站免费编写sql语句,它能够让用户直接在浏览器内练习SQL的语法,不需要安装任何软件。 链接如下: sqliteviz 注意: 在转写SQL语法时,关键字之间有一个特定的顺序,这个顺序会影响到…...

高等数学(下)题型笔记(八)空间解析几何与向量代数
目录 0 前言 1 向量的点乘 1.1 基本公式 1.2 例题 2 向量的叉乘 2.1 基础知识 2.2 例题 3 空间平面方程 3.1 基础知识 3.2 例题 4 空间直线方程 4.1 基础知识 4.2 例题 5 旋转曲面及其方程 5.1 基础知识 5.2 例题 6 空间曲面的法线与切平面 6.1 基础知识 6.2…...

今日科技热点速览
🔥 今日科技热点速览 🎮 任天堂Switch 2 正式发售 任天堂新一代游戏主机 Switch 2 今日正式上线发售,主打更强图形性能与沉浸式体验,支持多模态交互,受到全球玩家热捧 。 🤖 人工智能持续突破 DeepSeek-R1&…...

QT: `long long` 类型转换为 `QString` 2025.6.5
在 Qt 中,将 long long 类型转换为 QString 可以通过以下两种常用方法实现: 方法 1:使用 QString::number() 直接调用 QString 的静态方法 number(),将数值转换为字符串: long long value 1234567890123456789LL; …...

【从零学习JVM|第三篇】类的生命周期(高频面试题)
前言: 在Java编程中,类的生命周期是指类从被加载到内存中开始,到被卸载出内存为止的整个过程。了解类的生命周期对于理解Java程序的运行机制以及性能优化非常重要。本文会深入探寻类的生命周期,让读者对此有深刻印象。 目录 …...

【C++】纯虚函数类外可以写实现吗?
1. 答案 先说答案,可以。 2.代码测试 .h头文件 #include <iostream> #include <string>// 抽象基类 class AbstractBase { public:AbstractBase() default;virtual ~AbstractBase() default; // 默认析构函数public:virtual int PureVirtualFunct…...

comfyui 工作流中 图生视频 如何增加视频的长度到5秒
comfyUI 工作流怎么可以生成更长的视频。除了硬件显存要求之外还有别的方法吗? 在ComfyUI中实现图生视频并延长到5秒,需要结合多个扩展和技巧。以下是完整解决方案: 核心工作流配置(24fps下5秒120帧) #mermaid-svg-yP…...

Vue3中的computer和watch
computed的写法 在页面中 <div>{{ calcNumber }}</div>script中 写法1 常用 import { computed, ref } from vue; let price ref(100);const priceAdd () > { //函数方法 price 1price.value ; }//计算属性 let calcNumber computed(() > {return ${p…...

C# winform教程(二)----checkbox
一、作用 提供一个用户选择或者不选的状态,这是一个可以多选的控件。 二、属性 其实功能大差不差,除了特殊的几个外,与button基本相同,所有说几个独有的 checkbox属性 名称内容含义appearance控件外观可以变成按钮形状checkali…...

【若依】框架项目部署笔记
参考【SpringBoot】【Vue】项目部署_no main manifest attribute, in springboot-0.0.1-sn-CSDN博客 多一个redis安装 准备工作: 压缩包下载:http://download.redis.io/releases 1. 上传压缩包,并进入压缩包所在目录,解压到目标…...
