线性代数复习公式整理(自用/持续更新)
第一章 行列式
设A、B为n阶矩阵
∣ A T ∣ = ∣ A ∣ \left | A^T \right | =\left | A \right | AT =∣A∣
∣ A m ∣ = ∣ A ∣ m \left | A^m \right | =\left | A \right | ^m ∣Am∣=∣A∣m
∣ k A ∣ = k n ∣ A ∣ \left | kA \right | =k^n\left | A \right | ∣kA∣=kn∣A∣
∣ A B ∣ = ∣ A ∣ ∣ B ∣ \left | AB \right | =\left | A \right | \left | B \right | ∣AB∣=∣A∣∣B∣
若 A 可逆,则 ∣ A − 1 ∣ = 1 ∣ A ∣ 若A可逆,则\left | A^{-1} \right | =\frac{1}{\left | A\right | } 若A可逆,则 A−1 =∣A∣1
∣ A ∗ ∣ = ∣ A ∣ n − 1 \left | A^* \right | =\left | A \right | ^{n-1} ∣A∗∣=∣A∣n−1
A A ∗ = A ∗ A = ∣ A ∣ E AA^*=A^*A=\left | A \right | E AA∗=A∗A=∣A∣E
A ∗ = ∣ A ∣ A − 1 ( 若 A 可逆 ) A^*=\left | A \right | A^{-1}(若A可逆) A∗=∣A∣A−1(若A可逆)
A = ∣ A ∣ ( A ∗ ) − 1 A=\left | A \right | (A^*)^{-1} A=∣A∣(A∗)−1
∣ A 1 A 2 A 3 ∣ = A 1 A 2 A 3 , ∣ A 1 A 2 A 3 ∣ = − A 1 A 2 A 3 \begin{vmatrix}A_1 & & \\ & A_2 & \\ & &A_3 \end{vmatrix}=A_1A_2A_3, \begin{vmatrix} & &A_1 \\ & A_2 & \\A_3 & & \end{vmatrix}=-A_1A_2A_3 A1A2A3 =A1A2A3, A3A2A1 =−A1A2A3
设A为n阶矩阵,B为m阶矩阵,根据拉普拉斯展开定理有
∣ A 0 0 B ∣ = ∣ A C 0 B ∣ = ∣ A 0 C B ∣ = ∣ A ∣ ∣ B ∣ \begin{vmatrix}A & 0\\0 &B \end{vmatrix}=\begin{vmatrix}A & C\\0 &B \end{vmatrix}=\begin{vmatrix}A & 0\\C &B \end{vmatrix}=\left | A \right | \left | B \right | A00B = A0CB = AC0B =∣A∣∣B∣
∣ 0 A B 0 ∣ = ∣ C A B 0 ∣ = ∣ 0 A B C ∣ = ( − 1 ) m n ∣ A ∣ ∣ B ∣ \begin{vmatrix}0 & A\\B &0 \end{vmatrix}=\begin{vmatrix}C & A\\B &0 \end{vmatrix}=\begin{vmatrix}0 & A\\B &C \end{vmatrix}=(-1)^{mn}\left | A \right | \left | B \right | 0BA0 = CBA0 = 0BAC =(−1)mn∣A∣∣B∣
化“叉”型行列式
∣ a 0 . . . 0 b . . . A . . . c 0 . . . 0 d ∣ = ( a d − b c ) ∣ A ∣ , 其中 A 是方阵 , 且除了主对角线和副对角线以外其余所有的元素均为 0 \begin{vmatrix} a& 0& ...& 0&b \\ ...& & A& &... \\ c& 0 & ... &0 &d \end{vmatrix}=(ad-bc)\left | A \right | ,其中A是方阵,且除了主对角线和副对角线以外其余所有的元素均为0 a...c00...A...00b...d =(ad−bc)∣A∣,其中A是方阵,且除了主对角线和副对角线以外其余所有的元素均为0
化“ab”型行列式
∣ a b b . . . b b a b . . . b b b a . . . b . . . . . . . . . . . . b b b b . . . a ∣ = [ a + ( n − 1 ) b ] ( a − b ) n − 1 \begin{vmatrix} a& b& b& ...&b \\ b& a& b& ...&b \\ b& b& a& ...&b \\ ...& ...& ...& ...&b \\ b& b& b& ...&a \end{vmatrix}=[a+(n-1)b](a-b)^{n-1} abb...bbab...bbba...b...............bbbba =[a+(n−1)b](a−b)n−1
特征值求行列式
若题干可求得矩阵 A 的所有特征值 λ 1 , λ 2 . . . , λ n , 那么立即有 ∣ A ∣ = λ 1 λ 2 . . . λ n 若题干可求得矩阵A的所有特征值\lambda _1,\lambda _2...,\lambda _n,那么立即有\left | A \right | =\lambda _1\lambda _2...\lambda _n 若题干可求得矩阵A的所有特征值λ1,λ2...,λn,那么立即有∣A∣=λ1λ2...λn
第二章 矩阵
矩阵转置的性质
( A T ) T = A (A^T)^T=A (AT)T=A
( k A ) T = k A T (kA)^T=kA^T (kA)T=kAT
( A ± B ) T = A T ± B T (A\pm B)^T=A^T\pm B^T (A±B)T=AT±BT
( A B ) T = B T A T (AB)^T=B^TA^T (AB)T=BTAT
( A − 1 ) T = ( A T ) − 1 (A^{-1})^T=(A^T)^{-1} (A−1)T=(AT)−1
( A T ) m = ( A m ) T (A^T)^m=(A^m)^T (AT)m=(Am)T
矩阵伴随的性质
A ∗ = ∣ A ∣ A − 1 ( 若 A 可逆 ) A^*=\left | A \right | A^{-1}(若A可逆) A∗=∣A∣A−1(若A可逆)
A − 1 = 1 ∣ A ∣ A ∗ A^{-1}=\frac{1}{\left | A \right | } A^* A−1=∣A∣1A∗
( A T ) ∗ = ( A ∗ ) T (A^T)^*=(A^*)^T (AT)∗=(A∗)T
( k A ) ∗ = k n − 1 A ∗ (kA)^*=k^{n-1}A^* (kA)∗=kn−1A∗
( A B ) ∗ = B ∗ A ∗ (AB)^*=B^*A^* (AB)∗=B∗A∗
( a b c d ) ∗ = ( d − b − c a ) \begin{pmatrix} a & b\\ c&d \end{pmatrix}^*=\begin{pmatrix} d & -b\\ -c&a \end{pmatrix} (acbd)∗=(d−c−ba)
相关文章:
)
线性代数复习公式整理(自用/持续更新)
第一章 行列式 设A、B为n阶矩阵 ∣ A T ∣ ∣ A ∣ \left | A^T \right | \left | A \right | AT ∣A∣ ∣ A m ∣ ∣ A ∣ m \left | A^m \right | \left | A \right | ^m ∣Am∣∣A∣m ∣ k A ∣ k n ∣ A ∣ \left | kA \right | k^n\left | A \right | ∣kA∣kn∣A…...
)
QEMU源码全解析34 —— Machine(4)
接前一篇文章:QEMU源码全解析33 —— Machine(3) 本文内容参考: 《趣谈Linux操作系统》 —— 刘超,极客时间 《QEMU/KVM》源码解析与应用 —— 李强,机械工业出版社 特此致谢! 上一回围绕DEF…...

引用Boost库 CMakeList的写法
引用Boost库 CMakeList的写法 flyfish 环境arm cmake_minimum_required(VERSION 3.5)project(example LANGUAGES CXX)set(CMAKE_CXX_STANDARD 11) set(CMAKE_CXX_STANDARD_REQUIRED ON)set(BOOST_PREFIX /media/Boost/build/out/arm64-v8a/) set(BOOST_INCLUDE_DIR "${…...

Kibana 可视化数据分析以及es常用的数据分析函数
一、Kibana 可视化数据分析 1、Discover 的使用及生成报表:https://elasticstack.blog.csdn.net/article/details/131119502 2、Dashboard的使用:https://elasticstack.blog.csdn.net/article/details/131121890 该文档主要介绍Dashboard中的Lens使用…...

golang云原生怎么学?
学习golang云原生有哪些好处,他们的优缺点又有哪些? 一.好处有哪些? 1.高效性能:Golang是一门编译型语言,具有卓越的执行效率和并发处理能力。在云原生环境中,高效的性能对于应对大规模和高负载的分布式系…...
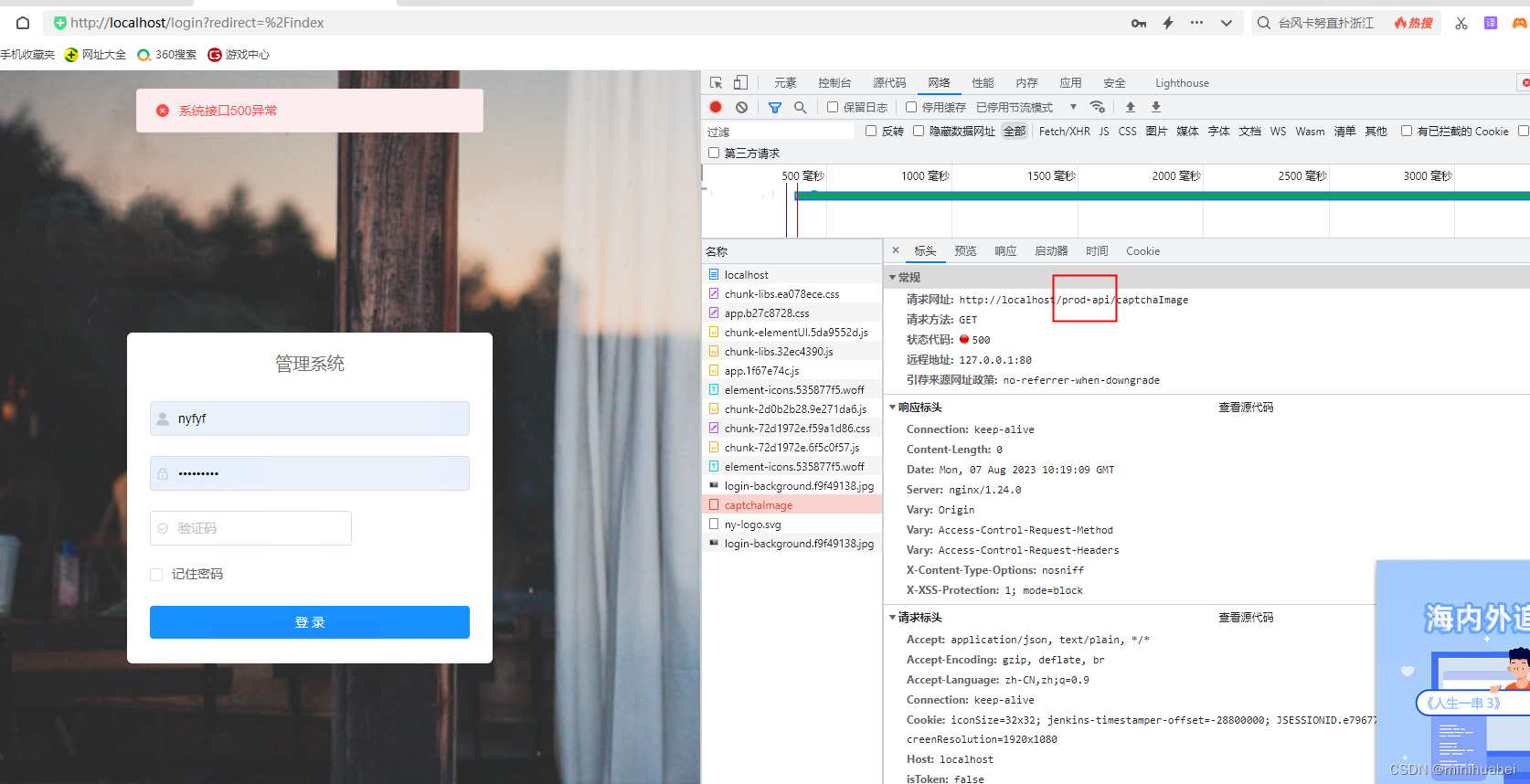
Jenkins+Nginx+vue
安装nodejs 在这里插入图片描述 echo off xcopy C:\ProgramData\Jenkins\.jenkins\workspace\super_manage_vue\dist F:\java\www\super_manage_vue\ /s /e /y echo 复制文件完成 exit安装niginx 配置文件如下 #user nobody; worker_processes 1;#error_log logs/error.lo…...

【vue 监听页面滑动到底部】
监听页面滑动到底部 IntersectionObserverscroll 事件监听器 IntersectionObserver 在 Vue 中监听触底可以通过使用IntersectionObserver实现。IntersectionObserver是一个可以异步观察目标元素与其祖先或视窗交叉状态的API。当目标元素进入或退出视口时,会触发Int…...
创建型设计模式:2、单例模式(C++实现实例 线程安全))
(一)创建型设计模式:2、单例模式(C++实现实例 线程安全)
目录 1、单例模式(Singleton Pattern)的含义 2、单例模式的优缺点 (1)优点: (2)缺点: 3、C实现单例模式的示例(简单) 4、C实现单例模式的示例ÿ…...

《练习100》86~90
题目86 # 生成一个包含20个随机整数(100以内)的列表,对其中偶数索引(下标)的数据进行降序排列,奇数索引的元素不变 import random list1 [random.randint(0,100) for _ in range(20)] list2 list1[::2] …...

C++——命名空间、输入、输出
在我们接触C之前,C语言中有时候会有使用全局变量,全局变量在使用过程中可能会发生冲突,这个冲突有时会是我们与库之间的冲突,有时又会是我们自己定义的之间的冲突,那么这时候命名空间的出现将很好的解决这个问题&#…...
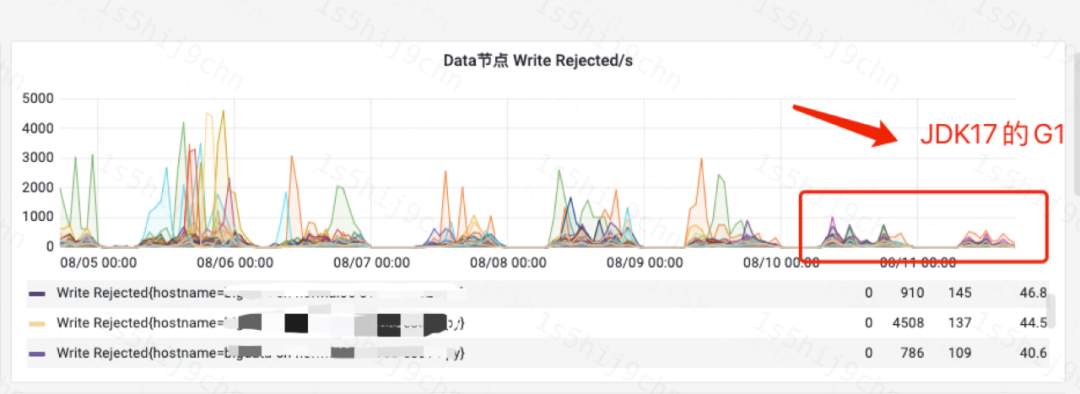
解锁滴滴ES的性能潜力:JDK 17和ZGC的升级之路
前文介绍了滴滴自研的ES强一致性多活是如何实现的,其中也提到为了提升查询性能和解决查询毛刺问题,滴滴ES原地升级JDK17和ZGC,在这个过程中我们遇到了哪些问题,怎样解决的,以及最终上线效果如何,这篇文章就…...

Permutation and Primes 2023牛客暑期多校训练营8 J
登录—专业IT笔试面试备考平台_牛客网 题目大意:给出一个数n,要求构造一个n的排列,满足相邻两个数的差或和是一个奇质数 2<n<1e5 思路:要满足相邻数的差或和是奇质数的话只有三种情况,要么当前数a[i]a[i-1]pr…...

centos如何配置IP地址?
CentOS如何查看和临时配置IP地址 CentOS系统中,可以通过使用ifconfig命令来查看当前本机的IP地址信息。输入ifconfig即可显示当前网络接口的IP地址、网络掩码和网关信息。如果需要设置临时IP地址,可以使用ifconfig命令后接网卡名称和需要设置的IP地址、网…...
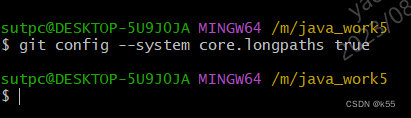
git clone 报错Filename too long
1.使用git clone代码,爆出Filename too long错误 2.原因分析 因为我很少看git clone日志,所以从未想过是clone异常,而且也看到代码clone下来了,所以我就显然以为代码clone成功,但是使用idea打开代码后发现大量代码无法…...

【雕爷学编程】Arduino动手做(184)---快餐盒盖,极低成本搭建机器人实验平台3
吃完快餐粥,除了粥的味道不错之外,我对个快餐盒的圆盖子产生了兴趣,能否做个极低成本的简易机器人呢?也许只需要二十元左右 知识点:轮子(wheel) 中国词语。是用不同材料制成的圆形滚动物体。简…...

redis String类型命令
Redis的String类型是一种简单的键值对数据结构,常用的String类型命令有: SET key value:设置指定key的值为value。GET key:获取指定key的值。DEL key:删除指定key及其对应的值。INCR key:将指定key的值加1…...
Blazor 简单组件(0):简单介绍
文章目录 前言说明环境安装 前言 Blazor 这个技术还是比较新,相关的UI组件还在完善,我这里提供一下我个人的组件开发。 说明 本UI组件是基于BootstrapBlazor(以下简称BB)开发。 BootstrapBlazor 文档 环境安装 C#小轮子:Visual Studio自…...

在vue3+vite项目中使用jsx语法
如果我掏出下图,阁下除了私信我加入学习群,还能如何应对? 正文开始 前言一、下载资源二、利用vite工具引入babel插件总结 前言 最近在为部署人员开发辅助部署的工具,技术栈是vue3viteelectron,在使用jsx语法时&#x…...

HCIA 路由器工作原理 及其 静态路由配置
目录 1、路由器工作原理 2、获取未知网段的方法: 3、静态路由 1)写法: 2)扩展配置 a、环回接口 配置命令: 环回接口的作用: b、手工汇总 手工汇总作用: c、路由黑洞 d、缺省路由 配置…...
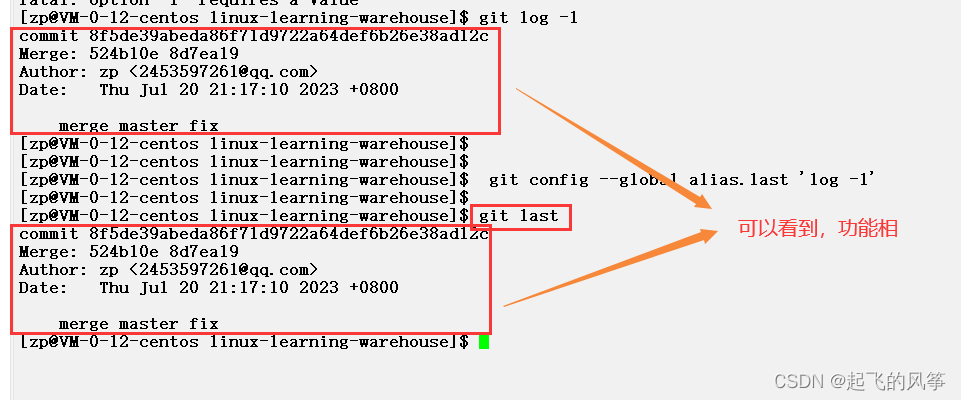
【Git】—— git的配置
目录 (一)忽略特殊⽂件 (二)给命令配置别名 (一)忽略特殊⽂件 在⽇常开发中,我们有些⽂件不想或者不应该提交到远端,⽐如保存了数据库密码的配置⽂件,那怎么让Git知道呢…...

MPNet:旋转机械轻量化故障诊断模型详解python代码复现
目录 一、问题背景与挑战 二、MPNet核心架构 2.1 多分支特征融合模块(MBFM) 2.2 残差注意力金字塔模块(RAPM) 2.2.1 空间金字塔注意力(SPA) 2.2.2 金字塔残差块(PRBlock) 2.3 分类器设计 三、关键技术突破 3.1 多尺度特征融合 3.2 轻量化设计策略 3.3 抗噪声…...

地震勘探——干扰波识别、井中地震时距曲线特点
目录 干扰波识别反射波地震勘探的干扰波 井中地震时距曲线特点 干扰波识别 有效波:可以用来解决所提出的地质任务的波;干扰波:所有妨碍辨认、追踪有效波的其他波。 地震勘探中,有效波和干扰波是相对的。例如,在反射波…...

基于Flask实现的医疗保险欺诈识别监测模型
基于Flask实现的医疗保险欺诈识别监测模型 项目截图 项目简介 社会医疗保险是国家通过立法形式强制实施,由雇主和个人按一定比例缴纳保险费,建立社会医疗保险基金,支付雇员医疗费用的一种医疗保险制度, 它是促进社会文明和进步的…...

剑指offer20_链表中环的入口节点
链表中环的入口节点 给定一个链表,若其中包含环,则输出环的入口节点。 若其中不包含环,则输出null。 数据范围 节点 val 值取值范围 [ 1 , 1000 ] [1,1000] [1,1000]。 节点 val 值各不相同。 链表长度 [ 0 , 500 ] [0,500] [0,500]。 …...

【2025年】解决Burpsuite抓不到https包的问题
环境:windows11 burpsuite:2025.5 在抓取https网站时,burpsuite抓取不到https数据包,只显示: 解决该问题只需如下三个步骤: 1、浏览器中访问 http://burp 2、下载 CA certificate 证书 3、在设置--隐私与安全--…...

解决本地部署 SmolVLM2 大语言模型运行 flash-attn 报错
出现的问题 安装 flash-attn 会一直卡在 build 那一步或者运行报错 解决办法 是因为你安装的 flash-attn 版本没有对应上,所以报错,到 https://github.com/Dao-AILab/flash-attention/releases 下载对应版本,cu、torch、cp 的版本一定要对…...

Axios请求超时重发机制
Axios 超时重新请求实现方案 在 Axios 中实现超时重新请求可以通过以下几种方式: 1. 使用拦截器实现自动重试 import axios from axios;// 创建axios实例 const instance axios.create();// 设置超时时间 instance.defaults.timeout 5000;// 最大重试次数 cons…...

自然语言处理——Transformer
自然语言处理——Transformer 自注意力机制多头注意力机制Transformer 虽然循环神经网络可以对具有序列特性的数据非常有效,它能挖掘数据中的时序信息以及语义信息,但是它有一个很大的缺陷——很难并行化。 我们可以考虑用CNN来替代RNN,但是…...

深入解析C++中的extern关键字:跨文件共享变量与函数的终极指南
🚀 C extern 关键字深度解析:跨文件编程的终极指南 📅 更新时间:2025年6月5日 🏷️ 标签:C | extern关键字 | 多文件编程 | 链接与声明 | 现代C 文章目录 前言🔥一、extern 是什么?&…...

【C++从零实现Json-Rpc框架】第六弹 —— 服务端模块划分
一、项目背景回顾 前五弹完成了Json-Rpc协议解析、请求处理、客户端调用等基础模块搭建。 本弹重点聚焦于服务端的模块划分与架构设计,提升代码结构的可维护性与扩展性。 二、服务端模块设计目标 高内聚低耦合:各模块职责清晰,便于独立开发…...
