DIDL4_前向传播与反向传播(模型参数的更新)
前向传播与反向传播
- 前向传播与反向传播的作用
- 前向传播及公式
- 前向传播范例
- 反向传播及公式
- 反向传播范例
- 小结
- 前向传播计算图
前向传播与反向传播的作用
在训练神经网络时,前向传播和反向传播相互依赖。
对于前向传播,我们沿着依赖的方向遍历计算图并计算其路径上的所有变量。
然后将这些用于反向传播,其中计算顺序与计算图的相反,用于计算w、b的梯度(即神经网络中的参数)。随后使用梯度下降算法来更新参数。
因此,在训练神经网络时,在初始化模型参数后, 我们交替使用前向传播和反向传播,利用反向传播给出的梯度来更新模型参数。
注意:
- 反向传播重复利用前向传播中存储的中间值,以避免重复计算。 带来的影响之一是我们需要保留中间值,直到反向传播完成。 这也是训练比单纯的预测需要更多的内存(显存)的原因之一。
- 这些中间值的大小与网络层的数量和批量的大小大致成正比。 因此,使用更大的批量来训练更深层次的网络更容易导致内存不足(out of memory)错误。
前向传播及公式
前向传播(forward propagation或forward pass) 指的是:按顺序(从输入层到输出层)计算和存储神经网络中每层的结果。
假设输入样本是 x∈Rd\mathbf{x}\in \mathbb{R}^dx∈Rd, 并且我们的隐藏层不包括偏置项。 这里的中间变量是:
z=W(1)x,\mathbf{z}= \mathbf{W}^{(1)} \mathbf{x},z=W(1)x,
其中W(1)∈Rh×d\mathbf{W}^{(1)} \in \mathbb{R}^{h \times d}W(1)∈Rh×d是隐藏层的权重参数。 将中间变量z∈Rh\mathbf{z}\in \mathbb{R}^hz∈Rh通过激活函数ϕ\phiϕ后, 我们得到长度为hhh的隐藏激活向量:
h=ϕ(z).\mathbf{h}= \phi (\mathbf{z}).h=ϕ(z).
隐藏变量h\mathbf{h}h也是一个中间变量。 假设输出层的参数只有权重W(2)∈Rq×h\mathbf{W}^{(2)} \in \mathbb{R}^{q \times h}W(2)∈Rq×h, 我们可以得到输出层变量,它是一个长度为qqq的向量:
o=W(2)h.\mathbf{o}= \mathbf{W}^{(2)} \mathbf{h}.o=W(2)h.
假设损失函数为lll,样本标签为yyy,我们可以计算单个数据样本的损失项
L=l(o,y).L = l(\mathbf{o}, y).L=l(o,y).
根据L2L_2L2正则化的定义,给定超参数λ\lambdaλ,正则化项为
s=λ2(∥W(1)∥F2+∥W(2)∥F2),s = \frac{\lambda}{2} \left(\|\mathbf{W}^{(1)}\|_F^2 + \|\mathbf{W}^{(2)}\|_F^2\right),s=2λ(∥W(1)∥F2+∥W(2)∥F2),
其中矩阵的Frobenius范数是将矩阵展平为向量后应用的L2L_2L2范数。 最后,模型在给定数据样本上的正则化损失为:
J=L+s.J = L + s.J=L+s.
前向传播范例
反向传播及公式
反向传播(backward propagation或backpropagation)指的是计算神经网络参数梯度的方法。也称“BP算法”
简言之,该方法根据微积分中的链式规则,按相反的顺序从输出层到输入层遍历网络。
该算法存储了计算某些参数梯度时所需的任何中间变量(偏导数)。
假设我们有函数Y=f(X)\mathsf{Y}=f(\mathsf{X})Y=f(X)和Z=g(Y)\mathsf{Z}=g(\mathsf{Y})Z=g(Y), 其中输入和输出X,Y,Z\mathsf{X}, \mathsf{Y}, \mathsf{Z}X,Y,Z是任意形状的张量。 利用链式法则,我们可以计算Z\mathsf{Z}Z关于X\mathsf{X}X的导数
∂Z∂X=prod(∂Z∂Y,∂Y∂X).\frac{\partial \mathsf{Z}}{\partial \mathsf{X}} = \text{prod}\left(\frac{\partial \mathsf{Z}}{\partial \mathsf{Y}}, \frac{\partial \mathsf{Y}}{\partial \mathsf{X}}\right).∂X∂Z=prod(∂Y∂Z,∂X∂Y).
反向传播的目的是计算梯度∂J/∂W(1)\partial J/\partial \mathbf{W}^{(1)}∂J/∂W(1)和∂J/∂W(2)\partial J/\partial \mathbf{W}^{(2)}∂J/∂W(2). 为此,我们应用链式法则,依次计算每个中间变量和参数的梯度。 计算的顺序与前向传播中执行的顺序相反,因为我们需要从计算图的结果开始,并朝着参数的方向努力。
- 计算目标函数J=L+sJ=L+sJ=L+s相对于损失项LLL和正则项sss的梯度
∂J∂L=1and∂J∂s=1.\frac{\partial J}{\partial L} = 1 \; \text{and} \; \frac{\partial J}{\partial s} = 1.∂L∂J=1and∂s∂J=1. - 根据链式法则计算目标函数关于输出层变量o\mathbf{o}o的梯度:
∂J∂o=prod(∂J∂L,∂L∂o)=∂L∂o∈Rq.\frac{\partial J}{\partial \mathbf{o}} = \text{prod}\left(\frac{\partial J}{\partial L}, \frac{\partial L}{\partial \mathbf{o}}\right) = \frac{\partial L}{\partial \mathbf{o}} \in \mathbb{R}^q.∂o∂J=prod(∂L∂J,∂o∂L)=∂o∂L∈Rq. - 计算正则化项相对于两个参数的梯度:
∂s∂W(1)=λW(1)and∂s∂W(2)=λW(2).\frac{\partial s}{\partial \mathbf{W}^{(1)}} = \lambda \mathbf{W}^{(1)} \; \text{and} \; \frac{\partial s}{\partial \mathbf{W}^{(2)}} = \lambda \mathbf{W}^{(2)}.∂W(1)∂s=λW(1)and∂W(2)∂s=λW(2). - 计算最接近输出层的模型参数的梯度 ∂J/∂W(2)∈Rq×h\partial J/\partial \mathbf{W}^{(2)} \in \mathbb{R}^{q \times h}∂J/∂W(2)∈Rq×h。 使用链式法则得出:
∂J∂W(2)=prod(∂J∂o,∂o∂W(2))+prod(∂J∂s,∂s∂W(2))=∂J∂oh⊤+λW(2).\frac{\partial J}{\partial \mathbf{W}^{(2)}}= \text{prod}\left(\frac{\partial J}{\partial \mathbf{o}}, \frac{\partial \mathbf{o}}{\partial \mathbf{W}^{(2)}}\right) + \text{prod}\left(\frac{\partial J}{\partial s}, \frac{\partial s}{\partial \mathbf{W}^{(2)}}\right)= \frac{\partial J}{\partial \mathbf{o}} \mathbf{h}^\top + \lambda \mathbf{W}^{(2)}.∂W(2)∂J=prod(∂o∂J,∂W(2)∂o)+prod(∂s∂J,∂W(2)∂s)=∂o∂Jh⊤+λW(2). - 为了获得关于W(1)\mathbf{W}^{(1)}W(1)的梯度,我们需要继续沿着输出层到隐藏层反向传播。 关于隐藏层输出的梯度∂J/∂h∈Rh\partial J/\partial \mathbf{h} \in \mathbb{R}^h∂J/∂h∈Rh由下式给出:
∂J∂h=prod(∂J∂o,∂o∂h)=W(2)⊤∂J∂o.\frac{\partial J}{\partial \mathbf{h}} = \text{prod}\left(\frac{\partial J}{\partial \mathbf{o}}, \frac{\partial \mathbf{o}}{\partial \mathbf{h}}\right) = {\mathbf{W}^{(2)}}^\top \frac{\partial J}{\partial \mathbf{o}}.∂h∂J=prod(∂o∂J,∂h∂o)=W(2)⊤∂o∂J. - 由于激活函数ϕ\phiϕ是按元素计算的, 计算中间变量z\mathbf{z}z的梯度∂J/∂z∈Rh\partial J/\partial \mathbf{z} \in \mathbb{R}^h∂J/∂z∈Rh需要使用按元素乘法运算符,我们用⊙\odot⊙表示:
∂J∂z=prod(∂J∂h,∂h∂z)=∂J∂h⊙ϕ′(z).\frac{\partial J}{\partial \mathbf{z}} = \text{prod}\left(\frac{\partial J}{\partial \mathbf{h}}, \frac{\partial \mathbf{h}}{\partial \mathbf{z}}\right) = \frac{\partial J}{\partial \mathbf{h}} \odot \phi'\left(\mathbf{z}\right).∂z∂J=prod(∂h∂J,∂z∂h)=∂h∂J⊙ϕ′(z). - 最后,我们可以得到最接近输入层的模型参数的梯度 ∂J/∂W(1)∈Rh×d\partial J/\partial \mathbf{W}^{(1)} \in \mathbb{R}^{h \times d}∂J/∂W(1)∈Rh×d。 根据链式法则,我们得到:
∂J∂W(1)=prod(∂J∂z,∂z∂W(1))+prod(∂J∂s,∂s∂W(1))=∂J∂zx⊤+λW(1).\frac{\partial J}{\partial \mathbf{W}^{(1)}} = \text{prod}\left(\frac{\partial J}{\partial \mathbf{z}}, \frac{\partial \mathbf{z}}{\partial \mathbf{W}^{(1)}}\right) + \text{prod}\left(\frac{\partial J}{\partial s}, \frac{\partial s}{\partial \mathbf{W}^{(1)}}\right) = \frac{\partial J}{\partial \mathbf{z}} \mathbf{x}^\top + \lambda \mathbf{W}^{(1)}.∂W(1)∂J=prod(∂z∂J,∂W(1)∂z)+prod(∂s∂J,∂W(1)∂s)=∂z∂Jx⊤+λW(1).
反向传播范例
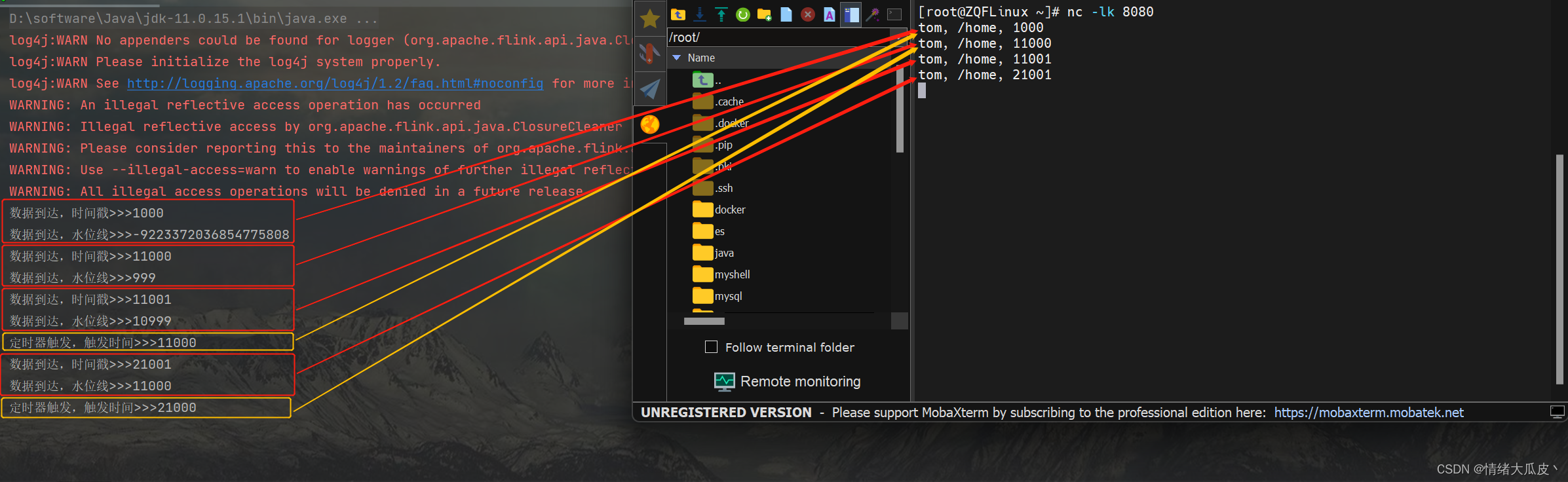
假设输入x = 1.5,模型初始参数w=0.8,b=0.2。学习率为0.1,则过程如下图:
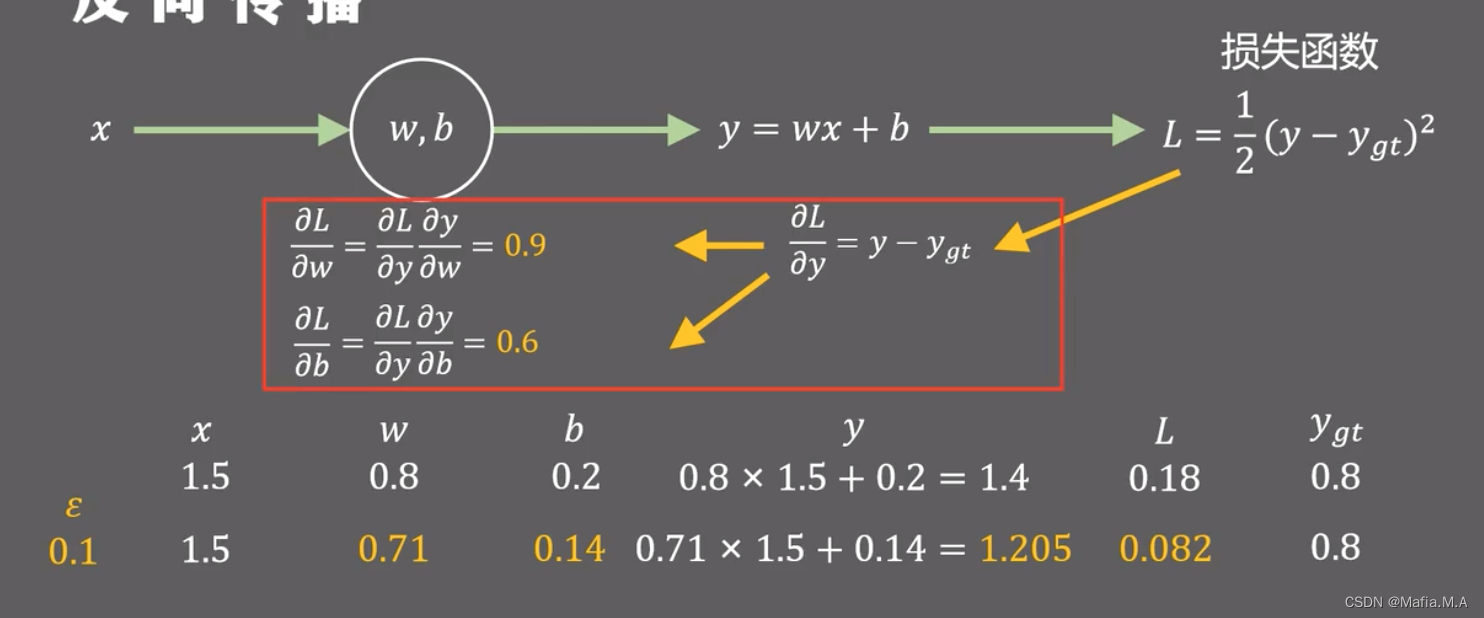
当有两层的时候:
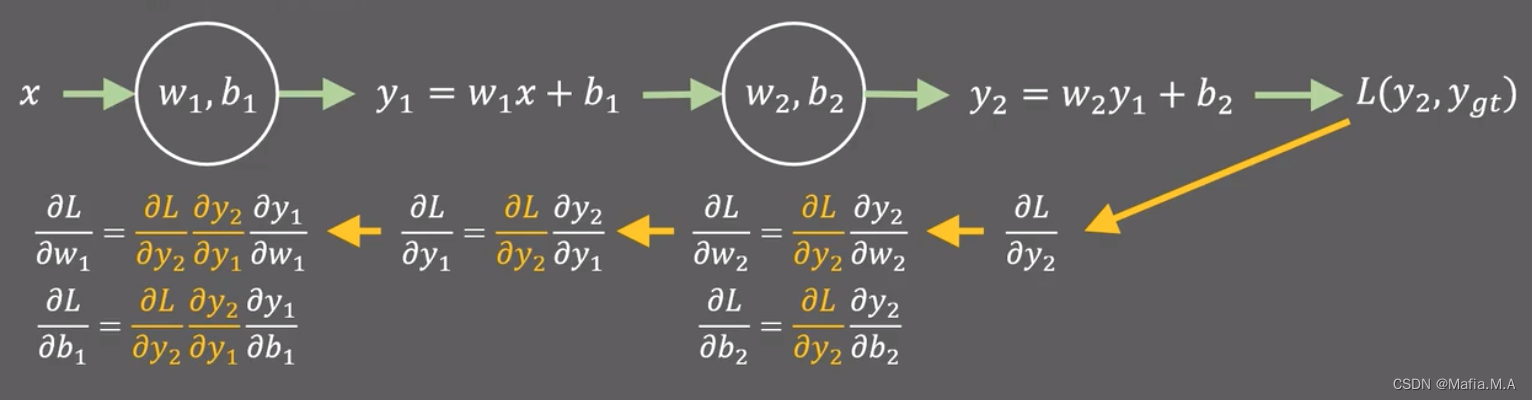
小结
- 前向传播在神经网络定义的计算图中按顺序计算和存储中间变量,它的顺序是从输入层到输出层。
- 反向传播按相反的顺序(从输出层到输入层)计算和存储神经网络的中间变量和参数的梯度。
- 在训练深度学习模型时,前向传播和反向传播是相互依赖的。
- 训练比预测需要更多的内存。
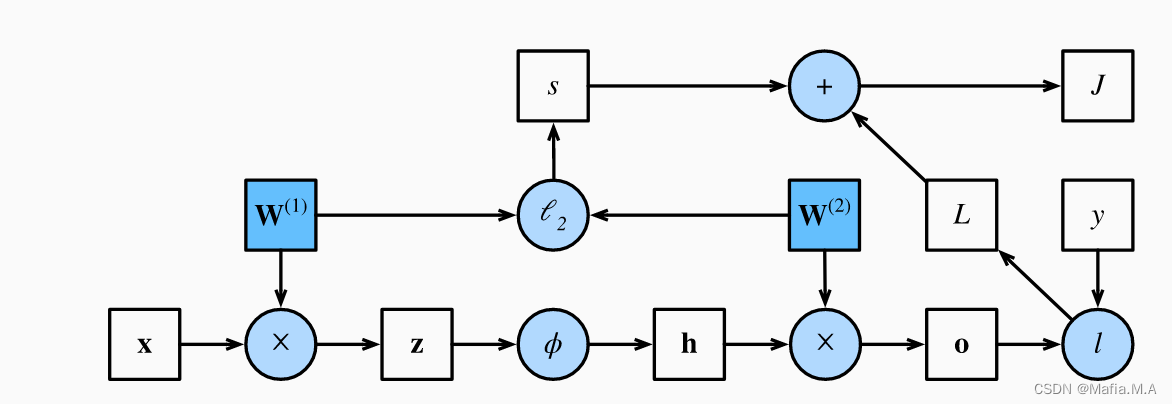
前向传播计算图
其中正方形表示变量,圆圈表示操作符。 左下角表示输入,右上角表示输出。 注意显示数据流的箭头方向主要是向右和向上的。
相关文章:

DIDL4_前向传播与反向传播(模型参数的更新)
前向传播与反向传播前向传播与反向传播的作用前向传播及公式前向传播范例反向传播及公式反向传播范例小结前向传播计算图前向传播与反向传播的作用 在训练神经网络时,前向传播和反向传播相互依赖。 对于前向传播,我们沿着依赖的方向遍历计算图并计算其路…...

链表学习之链表划分
链表解题技巧 额外的数据结构(哈希表);快慢指针;虚拟头节点; 链表划分 将单向链表值划分为左边小、中间相等、右边大的形式。中间值为pivot划分值。 要求:调整之后节点的相对次序不变,时间复…...

(考研湖科大教书匠计算机网络)第五章传输层-第一、二节:传输层概述及端口号、复用分用等概念
获取pdf:密码7281专栏目录首页:【专栏必读】考研湖科大教书匠计算机网络笔记导航 文章目录一:传输层概述(1)概述(2)从计算机网络体系结构角度看传输层(3)传输层意义二&am…...

C#:Krypton控件使用方法详解(第七讲) ——kryptonHeader
今天介绍的Krypton控件中的kryptonHeader,下面开始介绍这个控件的属性:控件的样子如上图所示,从上面控件外观来看,这个控件有三部分组成。第一部分是前面的图片,第二部分是kryptonHeader1文本,第三部分是控…...

5年软件测试工程师分享的自动化测试经验,一定要看
今天给大家分享一个华为的软件测试工程师分享的关于自动化测试的经验及干货。真的后悔太晚找他要了, 纯干货。一定要看完! 1.什么是自动化测试? 用程序测试程序,用代码取代思考,用脚本运行取代手工测试。自动化测试涵…...

什么是猜疑心理?小猫测试网科普小作文
什么是猜疑心理?猜疑心理是说一个人心中想法偏离了客观事实,牵强附会,往往是指不好的一面,对别人的一言一行都充满了不良的解读,认为这些对自己都有针对性,目的性,对自己都是不利的。猜疑心理重…...

Redis命令行对常用数据结构String、list、set、zset、hash等增删改查操作
1.Redis命令的小套路 - NX:not exist - EX:expire - M:multi 2.基本操作 ①切换数据库 Redis默认有16个数据库。 115 # Set the number of databases. The default database is DB 0, you can select 116 # a different one on a per-con…...

mycobot 使用教程
(1) 树莓派4B ubuntu系统调整swap空间与使SD卡快速扩容参考:https://www.bilibili.com/read/cv14825069https://blog.csdn.net/weixin_45824920/article/details/114381292?spm1001.2101.3001.6650.1&utm_mediumdistribute.pc_relevant.none-task-blog-2%7Edef…...
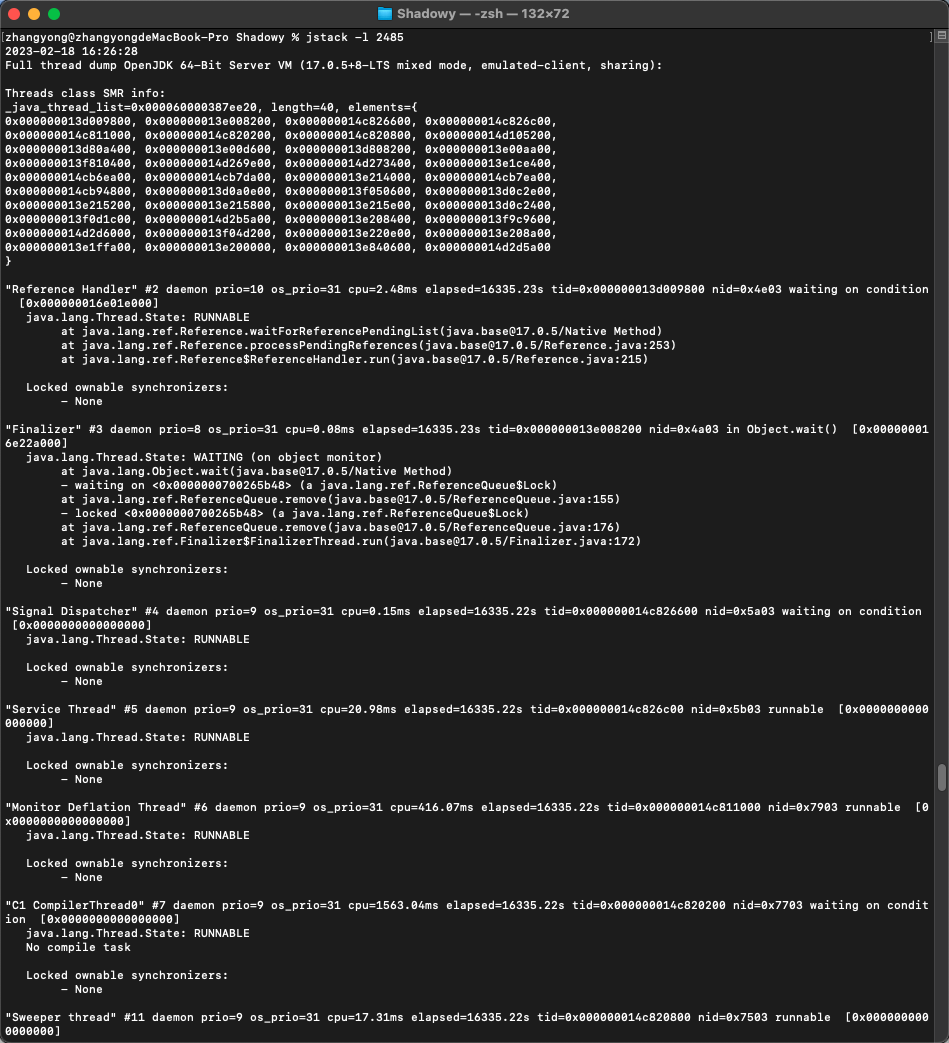
JVM学习总结,虚拟机性能监控、故障处理工具:jps、jstat、jinfo、jmap、Visual VM、jstack等
上篇:JVM学习总结,全面介绍运行时数据区域、各类垃圾收集器的原理使用、内存分配回收策略 参考资料:《深入理解Java虚拟机》第三版 文章目录三,虚拟机性能监控、故障处理工具1)jps:虚拟机进程状况工具2&…...

指针笔记(指针数组和指向数组的指针,数组中a和a的区别等)
指针数组和指向数组的指针 int *p[4]和int (*p)[4]有何区别? 前者是一个指针数组,数组大小为4,每一个元素都是一个指向int的指针 后者是指向int[4]类型数组的指针 以上代码若运行会报如下错误 main函数中定义的a数组本质是一个指向int[2]的…...

MySQL ---基础概念
目录 餐前小饮:什么是服务器?什么是数据库服务器? 一、数据库服务软件 1. 常见数据库产品 2.如何开启和停止MySQL服务 二、数据库术语及语法 1.数据库术语 2.SQL语法结构 3.SQL 语法要点 三、SQL分类 1.数据定义语言(D…...
【基础】Flink -- ProcessFunction
Flink -- ProcessFunction处理函数概述处理函数基本处理函数 ProcessFunction按键分区处理函数 KeyedProcessFunction定时器与定时服务基于处理时间的分区处理函数基于事件时间的分区处理函数窗口处理函数 ProcessWindowFunction应用案例 -- Top N处理函数概述 为了使代码拥有…...
JavaEE|网络编程基础与Socket套接字
文章目录一、为什么需要网络编程二、什么是网络编程三、网络编程中的基本概念1.发送端和接收端2.请求和响应3.客户端和服务端4.常见的客户端服务端模型四、Socket套接字概念及分类1.概念2.分类1)流套接字:使用传输层TCP协议2)数据报套接字&am…...

【SpringBoot】基础协议及邮件配置整合
一、名词概念解释 什么是POP3、SMTP和IMAP? 简单的说:POP3和IMAP是用来从服务器上下载邮件的。SMTP适用于发送或中转信件时找到下一个目的地。所以我们发送邮件应该使用SMTP协议。 POP3、SMTP和IMAP协议介绍 IMAP和POP3有什么区别?什么是免费…...
pytorch配置—什么是CUDA,什么是CUDNN、在配置pytorch虚拟环境中遇到的问题、在安装gpu—pytorch中遇到的问题
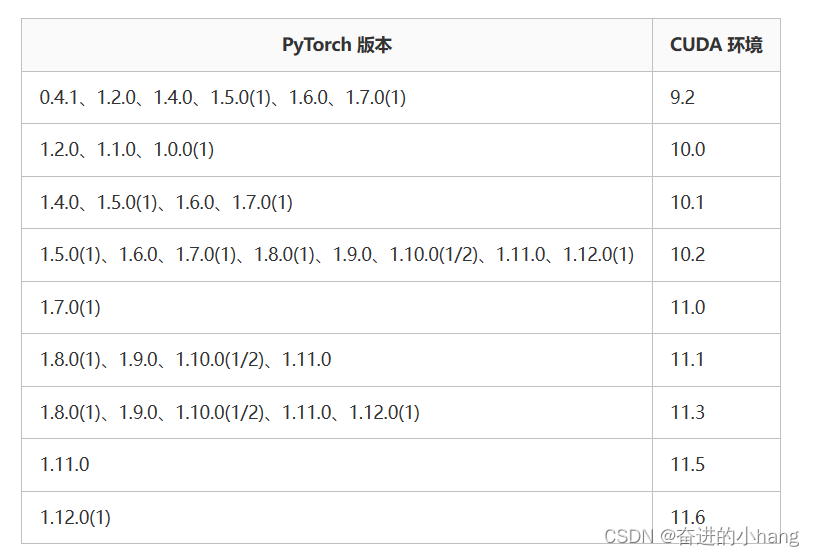
1.什么是CUDA,什么是CUDNN (1)什么是CUDA CUDA(ComputeUnified Device Architecture),是显卡厂商NVIDIA推出的运算平台。 CUDA是一种由NVIDIA推出的通用并行计算架构,该架构使GPU能够解决复杂的计算问题。 ࿰…...
jfr引起的一次jvm异常记录
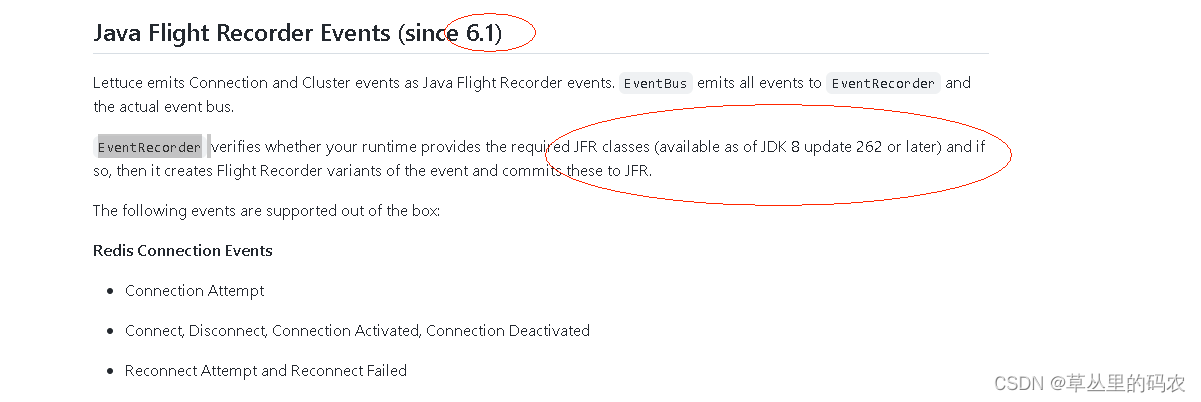
业务生产启动时,20个节点有1-2个节点因为jvm问题出现启动失败,k8s自动重启后正常。在测试环境2个节点下偶现 排查思路: 先拿到hs_err_pid的jvm错误文件找到当前线程和内部错误信息 hs_err_pid 文件分析 当前线程:lettuce的线程…...

Java智慧校园平台源码:SaaS模式智慧校园运营云平台源码
校班务管理:评价管理: 1.web端/教师端小程序编辑点评 多元化评价,捕捉学生闪光点全方位评价,自定义评价类型、 评价信息实时推送至家长、AI智能点评 班级报表一键导出,智能评测学生在校表现,老师、家长实…...
【yolov5】将标注好的数据集进行划分(附完整可运行python代码)
问题描述 准备使用yolov5训练自己的模型,自己将下载的开源数据集按照自己的要求重新标注了一下,然后现在对其进行划分。 问题分析 划分数据集主要的步骤就是,首先要将数据集打乱顺序,然后按照一定的比例将其分为训练集…...

es-05分词器
文章目录分词器1 normalization:文档规范化,提高召回率2 字符过滤器(character filter):分词之前的预处理,过滤无用字符3 令牌过滤器(token filter):停用词、时态转换、大小写转换、…...

已解决zipfile.BadZipFile: File is not a zip file
已解决Python openpyxl 读取Excel文件,抛出异常zipfile.BadZipFile: File is not a zip file的正确解决,亲测有效!!! 文章目录报错问题报错翻译报错原因解决方法联系博主免费帮忙解决报错报错问题 一个小伙伴遇到问题跑…...

C++:std::is_convertible
C++标志库中提供is_convertible,可以测试一种类型是否可以转换为另一只类型: template <class From, class To> struct is_convertible; 使用举例: #include <iostream> #include <string>using namespace std;struct A { }; struct B : A { };int main…...

Unity3D中Gfx.WaitForPresent优化方案
前言 在Unity中,Gfx.WaitForPresent占用CPU过高通常表示主线程在等待GPU完成渲染(即CPU被阻塞),这表明存在GPU瓶颈或垂直同步/帧率设置问题。以下是系统的优化方案: 对惹,这里有一个游戏开发交流小组&…...

练习(含atoi的模拟实现,自定义类型等练习)
一、结构体大小的计算及位段 (结构体大小计算及位段 详解请看:自定义类型:结构体进阶-CSDN博客) 1.在32位系统环境,编译选项为4字节对齐,那么sizeof(A)和sizeof(B)是多少? #pragma pack(4)st…...

Docker 运行 Kafka 带 SASL 认证教程
Docker 运行 Kafka 带 SASL 认证教程 Docker 运行 Kafka 带 SASL 认证教程一、说明二、环境准备三、编写 Docker Compose 和 jaas文件docker-compose.yml代码说明:server_jaas.conf 四、启动服务五、验证服务六、连接kafka服务七、总结 Docker 运行 Kafka 带 SASL 认…...

java调用dll出现unsatisfiedLinkError以及JNA和JNI的区别
UnsatisfiedLinkError 在对接硬件设备中,我们会遇到使用 java 调用 dll文件 的情况,此时大概率出现UnsatisfiedLinkError链接错误,原因可能有如下几种 类名错误包名错误方法名参数错误使用 JNI 协议调用,结果 dll 未实现 JNI 协…...

基于当前项目通过npm包形式暴露公共组件
1.package.sjon文件配置 其中xh-flowable就是暴露出去的npm包名 2.创建tpyes文件夹,并新增内容 3.创建package文件夹...

Unsafe Fileupload篇补充-木马的详细教程与木马分享(中国蚁剑方式)
在之前的皮卡丘靶场第九期Unsafe Fileupload篇中我们学习了木马的原理并且学了一个简单的木马文件 本期内容是为了更好的为大家解释木马(服务器方面的)的原理,连接,以及各种木马及连接工具的分享 文件木马:https://w…...

莫兰迪高级灰总结计划简约商务通用PPT模版
莫兰迪高级灰总结计划简约商务通用PPT模版,莫兰迪调色板清新简约工作汇报PPT模版,莫兰迪时尚风极简设计PPT模版,大学生毕业论文答辩PPT模版,莫兰迪配色总结计划简约商务通用PPT模版,莫兰迪商务汇报PPT模版,…...

什么是VR全景技术
VR全景技术,全称为虚拟现实全景技术,是通过计算机图像模拟生成三维空间中的虚拟世界,使用户能够在该虚拟世界中进行全方位、无死角的观察和交互的技术。VR全景技术模拟人在真实空间中的视觉体验,结合图文、3D、音视频等多媒体元素…...
 Module Federation:Webpack.config.js文件中每个属性的含义解释)
MFE(微前端) Module Federation:Webpack.config.js文件中每个属性的含义解释
以Module Federation 插件详为例,Webpack.config.js它可能的配置和含义如下: 前言 Module Federation 的Webpack.config.js核心配置包括: name filename(定义应用标识) remotes(引用远程模块࿰…...
