第三章 图论 No.8最近公共祖先lca, tarjan与次小生成树
文章目录
- lca
- Tarjan
- 板子题:1172. 祖孙询问
- lca或tarjan:1171. 距离
- 356. 次小生成树
- 352. 闇の連鎖

lca
O ( m l o g n ) O(mlogn) O(mlogn),n为节点数量,m为询问次数,lca是一种在线处理询问的算法
自己也是自己的祖先
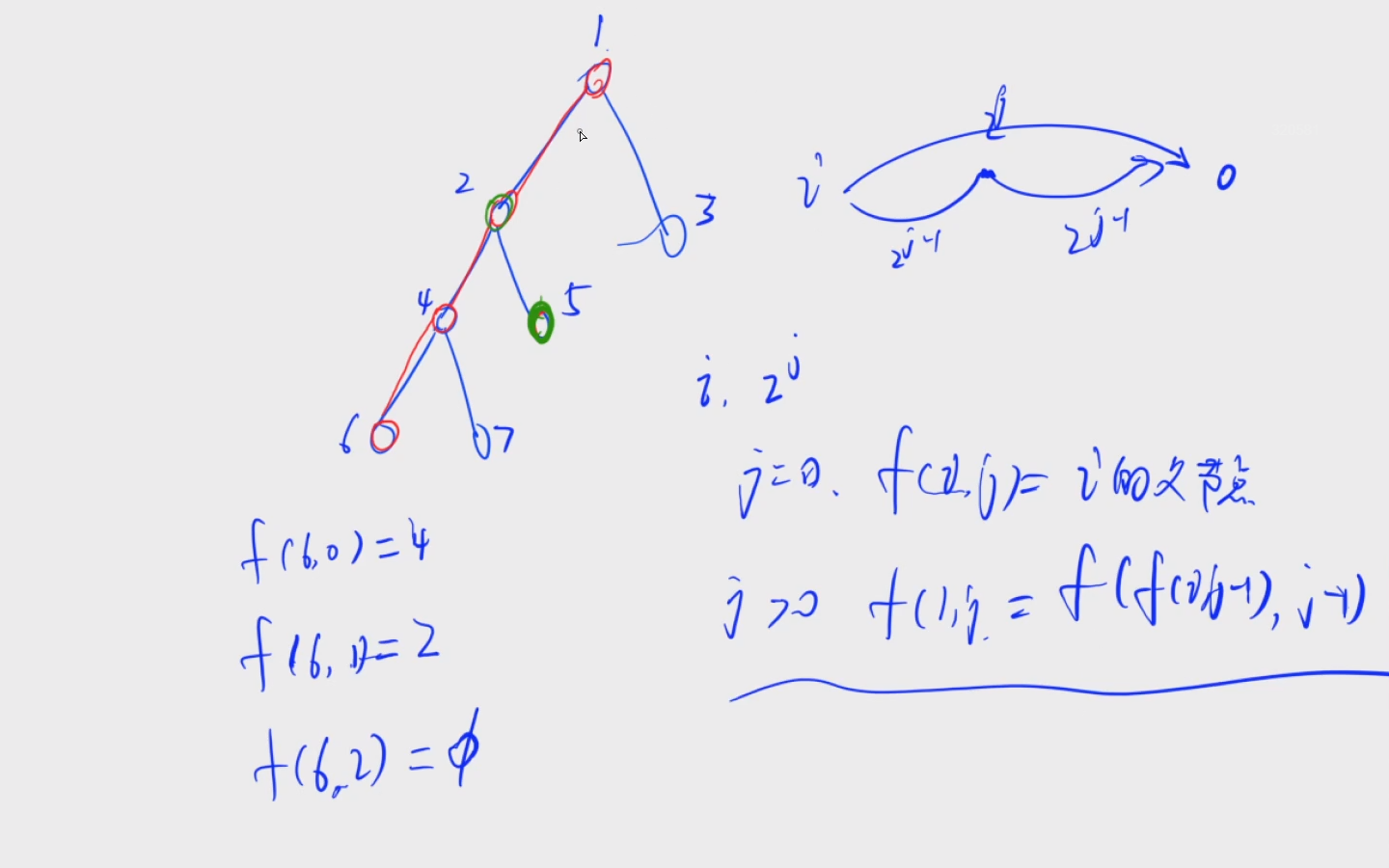
倍增:
f a ( i , j ) fa(i, j) fa(i,j)表示从i开始,向上走 2 j 2^j 2j步走到的点
j = 0,走到父节点
j > 0,分两步走,先走到 2 j − 1 2^{j-1} 2j−1步再走 2 j − 1 2^{j-1} 2j−1步,那么一共就会走 2 j 2^j 2j步, f a ( i , j ) = f a ( f a ( i , j − 1 ) , j − 1 ) fa(i, j) = fa(fa(i, j-1), j-1) fa(i,j)=fa(fa(i,j−1),j−1)
d e p t h ( i ) depth(i) depth(i)表示层数
- 将两点跳到同一层
- 让两个点同时往上跳,直到跳到公共祖先的下一层
第一步:基于二进制的思想,x和y之间的层数差距为 d e p t h ( x ) − d e p t h ( y ) depth(x) - depth(y) depth(x)−depth(y),假设y的层数小于x的层数,此时x要往上跳
若要跳k层,那么根据k的二进制表示将k拆分成多个2的幂相加,由于我们已经预处理了 f ( i , j ) f(i, j) f(i,j),所以根据 f ( i , j ) f(i, j) f(i,j)的值往上跳即可
当 f ( x , k ) = f ( y , k ) f(x, k) = f(y, k) f(x,k)=f(y,k)时,即x往上跳k步和y往上跳k步后,位于同一个位置,此时找到了一个公共祖先,但不是最近公共祖先,所以这里要减小k的值,直到 f ( x , k ) ≠ f ( y , k ) f(x, k) ≠ f(y, k) f(x,k)=f(y,k),此时才找到了最近公共祖先
规定 d e p t h ( 0 ) = 0 depth(0) = 0 depth(0)=0,0号点为哨兵,位于第0层,根节点位于第一层
向上跳 2 k 2^k 2k步后,若跳出了这颗树,那么 f ( i , k ) = 0 f(i, k) = 0 f(i,k)=0
预处理depth和fa的板子:
void bfs(int root)
{memset(dis, 0x3f, sizeof(dis));q[tt ++ ] = root;depth[root] = 1, depth[0] = 0;while (tt >= hh){int x = q[hh ++ ];for (int i = h[x]; i != -1; i = ne[i]){int y = e[i];if (depth[y] > depth[x] + 1){depth[y] = depth[x] + 1;q[tt ++ ] = y;fa[y][0] = x;for (int k = 1; k <= c; ++ k )fa[y][k] = fa[fa[y][k - 1]][k - 1];}}}
}
lca板子:
int lca(int x, int y)
{if (depth[x] < depth[y]) swap(x, y);for (int k = c; k >= 0; -- k )if (depth[fa[x][k]] >= depth[y])x = fa[x][k];if (x == y) return y;for (int k = c; k >= 0; -- k )if (fa[x][k] != fa[y][k]){x = fa[x][k];y = fa[x][k];}return fa[x][0];
}
Tarjan
O ( n + m ) O(n + m) O(n+m) ,n为节点数量,m为询问次数
tarjan是一种离线处理询问的算法,是向上标记法的优化
在深度优先遍历时,将所有点分成三大类
- 已经遍历过且已经回溯的点
- 已经遍历但正在搜索的分支
- 还未搜索到的点
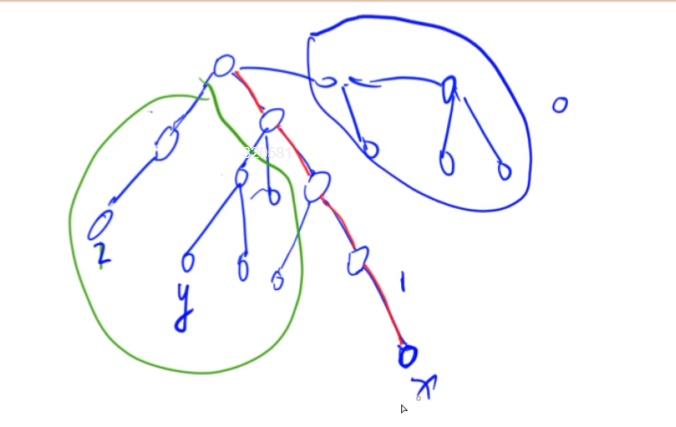
将已经遍历且回溯的点标记成2,正在遍历的点标记成1,未遍历的点标记成0
对于正在回溯的点,需要处理所有有关该点的询问信息:若询问的另外一个点已经遍历过(回溯完成),那么该点将被分到一个集合中,集合的代表点就是两点的最近公共祖先
比如上图,当前正在遍历x这个点,已经遍历完的点为绿色部分,这些点所属集合的代表点位于红色分支上
模板:
// 用dfs维护dis数组
void dfs(int x, int fa)
{for (int i = h[x]; i != -1; i = ne[i]){int y = e[i];if (y != fa){dis[y] = dis[x] + w[i];dfs(y, x);}}
}// tarjan处理询问
void tarjan(int x)
{st[x] = 1; // 当前正在遍历该点for (int i = h[x]; i != -1; i = ne[i]){int y = e[i];if (!st[y]) // 当前为遍历ydian{tarjan(y);p[y] = u;}}for (auto item : query[x]) // 处理有关当前节点的询问{int y = item.first, id = item.first; // id为该询问的唯一编号if (st[y] == 2) // 询问的另一点已经遍历过{int anc = find(y); // 找到集合的代表点,公共祖先res[id] = dis[x] + dis[y] - 2 * dis[anc]; // 根据id将答案存储到数组中}}st[x] = 2; // 当前节点遍历完
}
板子题:1172. 祖孙询问
1172. 祖孙询问 - AcWing题库
由于树的层数最大有40000层,所以一个节点最多向上跳 l o g 400000 log400000 log400000层,大概是一个大于 2 15 2^{15} 215小于 2 16 2^{16} 216的数,所以最多跳 2 16 − 1 2^{16} - 1 216−1层,二进制位取15即可
#include <iostream>
#include <cstring>
using namespace std;const int N = 4e4 + 10, M = 2 * N;
int h[N], e[M], ne[M], idx;
int q[N], hh, tt = -1;
int depth[N], fa[N][16]; // 最多跳2^16-1
int n;void add(int x, int y)
{e[idx] = y, ne[idx] = h[x], h[x] = idx ++ ;
}void bfs(int root)
{q[++ tt] = root;memset(depth, 0x3f, sizeof(depth));depth[0] = 0, depth[root] = 1;while (tt >= hh){int x = q[hh ++ ];for (int i = h[x]; i != -1; i = ne[i]){int y = e[i];if (depth[y] > depth[x] + 1){depth[y] = depth[x] + 1;fa[y][0] = x;q[++ tt ] = y;for (int k = 1; k <= 15; ++ k )fa[y][k] = fa[fa[y][k - 1]][k - 1];}}}
}int lca(int x, int y)
{if (depth[x] < depth[y]) swap(x, y);for (int k = 15; k >= 0; -- k )if (depth[fa[x][k]] >= depth[y])x = fa[x][k];if (x == y) return y;for (int k = 15; k >= 0; -- k )if (fa[x][k] != fa[y][k]){x = fa[x][k];y = fa[y][k];}return fa[x][0];
}int main()
{memset(h, -1, sizeof(h));scanf("%d", &n);int root;int a, b;for (int i = 0; i < n; ++ i ){scanf("%d%d", &a, &b);if (b == -1) root = a;else add(a, b), add(b, a);}bfs(root);int m;scanf("%d", &m);for (int i = 0; i < m; ++ i ){scanf("%d%d", &a, &b);int t = lca(a, b);if (t == a) puts("1");else if (t == b) puts("2");else puts("0");}return 0;
}
lca或tarjan:1171. 距离
1171. 距离 - AcWing题库
与上题一样,题目要处理很多询问,可以用lca或者离线tarjan解决
树的最短路问题可以从公共祖先的角度考虑,假设x和y的公共祖先为t, d i s ( t ) dis(t) dis(t)为根节点到t的距离,那么x和y之间的最短距离就是 d i s ( x ) + d i s ( y ) − 2 ∗ d i s ( t ) dis(x) + dis(y) - 2 * dis(t) dis(x)+dis(y)−2∗dis(t)
题目没有给定根节点,我们任意指定一个点为根节点即可
lca解法:
#include <iostream>
#include <cstring>
using namespace std;const int N = 1e4 + 10, M = 2 * N;
int h[N], e[M], ne[M], w[M], idx;
int depth[N], fa[N][16];
int q[N], hh, tt = -1;
int dis[N];void add(int x, int y, int d)
{e[idx] = y, ne[idx] = h[x], w[idx] = d, h[x] = idx ++ ;
}void dfs(int root)
{memset(depth, 0x3f, sizeof(depth));depth[0] = 0, depth[root] = 1;q[++ tt ] = root;while (tt >= hh){int x = q[hh ++ ];for (int i = h[x]; i != -1; i = ne[i]){int y = e[i];if (depth[y] > depth[x] + 1){depth[y] = depth[x] + 1;dis[y] = dis[x] + w[i];fa[y][0] = x;q[++ tt ] = y;for (int k = 1; k <= 15; ++ k )fa[y][k] = fa[fa[y][k - 1]][k - 1];}}}
}int lca(int x, int y)
{if (depth[x] < depth[y]) swap(x, y);for (int k = 15; k >= 0; -- k )if (depth[fa[x][k]] >= depth[y])x = fa[x][k];if (x == y) return y;for (int k = 15; k >= 0; -- k )if (fa[x][k] != fa[y][k]){x = fa[x][k];y = fa[y][k];}return fa[x][0];
}int main()
{memset(h, -1, sizeof(h));int n, m;scanf("%d%d", &n, &m);int x, y, d;for (int i = 0; i < n - 1; ++ i ){scanf("%d%d%d", &x, &y, &d);add(x, y, d), add(y, x, d);}dfs(1);for (int i = 0; i < m; ++ i ){scanf("%d%d", &x, &y);int t = lca(x, y);printf("%d\n", dis[x] + dis[y] - 2 * dis[t]);}return 0;
}
tarjan解法:
#include <iostream>
#include <cstring>
#include <vector>
using namespace std;const int N = 1e4 + 10, M = 2 * N;
typedef pair<int, int> PII;
vector<PII> query[N];
int h[N], e[M], ne[M], w[M], idx;
int res[M], dis[N], st[N], p[N];
int n, m;void add(int x, int y, int d)
{e[idx] = y, ne[idx] = h[x], w[idx] = d, h[x] = idx ++ ;
}void dfs(int x, int fa)
{for (int i = h[x]; i != -1; i = ne[i]){int y = e[i];if (y != fa){dis[y] = dis[x] + w[i];dfs(y, x);}}
}int find(int x)
{if (p[x] != x) p[x] = find(p[x]);return p[x];
}void tarjan(int x)
{st[x] = 1;for (int i = h[x]; i != -1; i = ne[i]){int y = e[i];if (!st[y]){tarjan(y);p[y] = x;}}for (auto item : query[x]){int y = item.first, id = item.second;if (st[y] == 2){int anc = find(y);res[id] = dis[x] + dis[y] - 2 * dis[anc];}}st[x] = 2;
}int main()
{memset(h, -1, sizeof(h));scanf("%d%d", &n, &m);int x, y, d;for (int i = 0; i < n - 1; ++ i ){scanf("%d%d%d", &x, &y, &d);add(x, y, d), add(y, x, d);}for (int i = 0; i < m; ++ i ){scanf("%d%d", &x, &y);query[x].push_back({y, i}); // 将查询的另一个点与查询编号保存query[y].push_back({x, i});}dfs(1, -1);for (int i = 1; i <= n; ++ i ) p[i] = i;tarjan(1);for (int i = 0; i < m; ++ i ) printf("%d\n", res[i]);return 0;
}
debug:维护的query信息要不同地插入两次
query[x].push_back({y, i});
query[y].push_back({x, i});
因为当前询问有关x的信息时,y可能没有遍历完,但是询问y有关的信息时,x是遍历完的
356. 次小生成树
356. 次小生成树 - AcWing题库
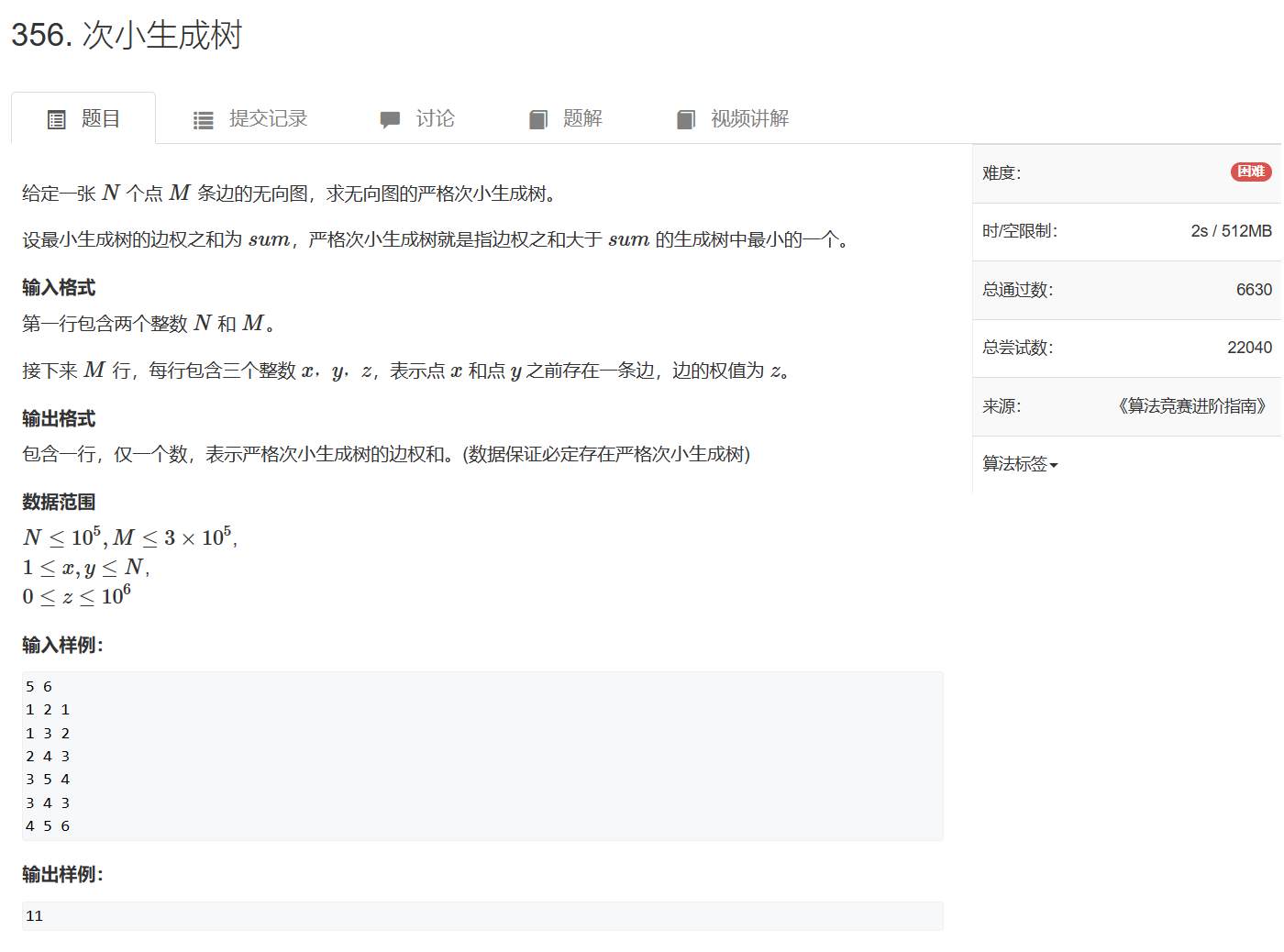
d 1 ( i , j ) d1(i, j) d1(i,j)表示从i往上跳 2 j 2^j 2j层后,路径上的最大边权
d 2 ( i , j ) d2(i, j) d2(i,j)表示从i往上跳 2 j 2^j 2j层后,路径上的次大边权
跳 2 j 2^j 2j步是一个类似分治的过程,分成两部分跳,这两部分依旧能分成两部分跳
路径上的最大值为每一段的最大值取max,次大值为所有子路径的最大值和次大值中的第二大,每次遍历子线段时维护信息即可
if (d > d1) d2 = d1, d1 = d;
else if (d != d1 && d > d2) d2 = d;
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;typedef long long LL;
const int N = 1e5 + 10, M = 3e5 + 10, INF = 0x3f3f3f3f;
struct Edge
{int x, y, w;bool f;bool operator<(const Edge& e) const {return w < e.w;}
}edges[M];int h[N], e[M], ne[M], w[M], idx;
int p[N], depth[N], fa[N][17];
int q[N], hh, tt = -1;
int d1[N][17], d2[N][17];
int d[M];
int n, m;void add(int x, int y, int d)
{e[idx] = y, ne[idx] = h[x], w[idx] = d, h[x] = idx ++ ;
}int find(int x)
{if (x != p[x]) p[x] = find(p[x]);return p[x];
}LL kruskal()
{LL res = 0;sort(edges, edges + m);for (int i = 1; i <= n; ++ i ) p[i] = i;for (int i = 0; i < m; ++ i ){auto t = edges[i];int x = t.x, y = t.y, w = t.w;int px = find(x), py = find(y);if (px != py){res += w;p[px] = py;edges[i].f = true;add(x, y, w), add(y, x, w);}}return res;
}void bfs()
{q[++ tt ] = 1;memset(depth, 0x3f, sizeof(depth));depth[0] = 0, depth[1] = 1;while (tt >= hh){int x = q[hh ++ ];for (int i = h[x]; i != -1; i = ne[i]){int y = e[i];if (depth[y] > depth[x] + 1){depth[y] = depth[x] + 1;fa[y][0] = x;d1[y][0] = w[i], d2[y][0] = -INF;q[++ tt ] = y;for (int k = 1; k <= 16; ++ k ){int mid = fa[y][k - 1];fa[y][k] = fa[mid][k - 1];d1[y][k] = d2[y][k] = -INF;int a[4] = { d1[mid][k - 1], d2[mid][k - 1], d1[y][k - 1], d2[y][k - 1] };for (int i = 0; i < 4; ++ i ){if (a[i] > d1[y][k]) d2[y][k] = d1[y][k], d1[y][k] = a[i];else if (a[i] != d1[y][k] && a[i] > d2[y][k]) d2[y][k] = a[i];}}}}}
}int lca(int x, int y, int w)
{int cnt = 0;if (depth[x] < depth[y]) swap(x, y);for (int k = 16; k >= 0; -- k )if (depth[fa[x][k]] >= depth[y]){d[cnt ++ ] = d1[x][k];d[cnt ++ ] = d2[x][k];x = fa[x][k];}if (x != y){for (int k = 16; k >= 0; -- k ){if (fa[x][k] != fa[y][k]){d[cnt ++ ] = d1[x][k], d[cnt ++ ] = d2[x][k];d[cnt ++ ] = d1[y][k], d[cnt ++ ] = d2[y][k];x = fa[x][k], y = fa[y][k];}d[cnt ++ ] = d1[x][0], d[cnt ++ ] = d2[x][0];d[cnt ++ ] = d1[y][0], d[cnt ++ ] = d2[y][0];}}int dmax1 = -INF, dmax2 = -INF;for (int i = 0; i < cnt; ++ i ){if (d[i] > dmax1) dmax2 = dmax1, dmax1 = d[i];else if (d[i] != dmax1 && d[i] > dmax2) dmax2 = d[i];}if (w > dmax1) return w - dmax1;return w - dmax2;
}int main()
{memset(h, -1, sizeof(h));scanf("%d%d", &n, &m);for (int i = 0; i < m; ++ i )scanf("%d%d%d", &edges[i].x, &edges[i].y, &edges[i].w);LL sum = kruskal(); // 最小生成树的权值bfs();LL res = 1e19;for (int i = 0; i < m; ++ i )if (!edges[i].f)res = min(res, sum + lca(edges[i].x, edges[i].y, edges[i].w));printf("%lld\n", res);return 0;
}
352. 闇の連鎖
352. 闇の連鎖 - AcWing题库

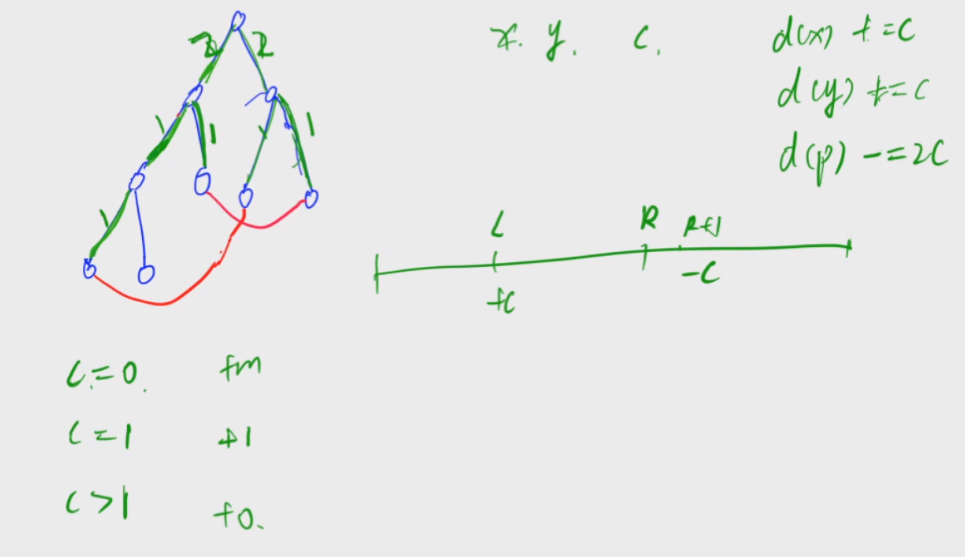
树上差分,将x到y的最短路径上所有的边加上c,若p为x和y的公共祖先,那么
d(x) += c, d(y) += c, d(p) -= 2c
如何计算某条边的权值?以这条边的子节点为根的子树中,所有边的权值相加为这条边的权值
在一颗树中,删除任意一条边,那么这颗树将被切成两个连通块
若向树中再添加一条边,那么这条非树边和树边就一定构成环,要向将此时的“树”切成两个连通块,就要删除环中的任意一条树边与这条非树边
题目限制只能先切树边,再切非树边,一共两次,两次过后还没有切成两个连通块,说明这个方案行不通
当切除树边,不用再切除非树边就得到两个连通块时,由于题目限制,还需要切除一条非树边,假设非树边有m条,那么此时可以选择m条边中的任意一条切除,此时的方案数为m
若切除树边后,还要再切除一条非树边,才能得到两个连通块时,此时的方案数为1,只能切除这条环中的非树边
若切除树边后,还要再切除大于一条的非树边,此时无法再切除,方案数为0
现在的问题是,如何知道切除某条树边后,还需要再切除几条非树边?
假设现在已经用树边建立了一棵树,此时再添加非树边将构成环,将环中的所有树边权值加1,假设初始权值为0,此时可以使用树上差分
然后遍历所有的树边,根据边权计算方案数
#include <iostream>
#include <cstring>
using namespace std;const int N = 1e5 + 10, M = 2e5 + 10;
int h[N], e[M], ne[M], idx;
int depth[N], fa[N][17];
int q[N], hh, tt = -1;
int d[N];
int n, m, ans;void add(int x ,int y)
{e[idx] = y, ne[idx] = h[x], h[x] = idx ++ ;
}void bfs()
{memset(depth, 0x3f, sizeof(depth));depth[0] = 0, depth[1] = 1;q[++ tt ] = 1;while (tt >= hh){int x = q[hh ++ ];for (int i = h[x]; i != -1; i = ne[i]){int y = e[i];if (depth[y] > depth[x] + 1){depth[y] = depth[x] + 1;fa[y][0] = x;q[++ tt ] = y;for (int k = 1; k <= 16; ++ k )fa[y][k] = fa[fa[y][k - 1]][k - 1];}}}
}int lca(int x, int y)
{if (depth[x] < depth[y]) swap(x, y);for (int k = 16; k >= 0; -- k )if (depth[fa[x][k]] >= depth[y])x = fa[x][k];if (x == y) return x;for (int k = 16; k >= 0; -- k )if (fa[x][k] != fa[y][k]){x = fa[x][k];y = fa[y][k];}return fa[x][0];
}int dfs(int x, int f)
{int res = d[x];for (int i = h[x]; i != -1; i = ne[i]){int y = e[i];if (f != y){int t = dfs(y, x);if (t == 0) ans += m;else if (t == 1) ans ++;res += t;}}return res;
}int main()
{memset(h, -1, sizeof(h));scanf("%d%d", &n, &m);int x, y;for (int i = 0; i < n - 1; ++ i ){ scanf("%d%d", &x, &y);add(x, y), add(y, x);}bfs();int res = 0;for (int i = 0; i < m; ++ i){scanf("%d%d", &x, &y);int p = lca(x, y);d[x] ++, d[y] ++, d[p] -= 2;}dfs(1, -1);printf("%d\n", ans);return 0;
}
相关文章:

第三章 图论 No.8最近公共祖先lca, tarjan与次小生成树
文章目录 lcaTarjan板子题:1172. 祖孙询问lca或tarjan:1171. 距离356. 次小生成树352. 闇の連鎖 lca O ( m l o g n ) O(mlogn) O(mlogn),n为节点数量,m为询问次数,lca是一种在线处理询问的算法 自己也是自己的祖先 倍…...
[Kubernetes]Kubeflow Pipelines - 基本介绍与安装方法
1. 背景 近些年来,人工智能技术在自然语言处理、视觉图像和自动驾驶方面都取得不小的成就,无论是工业界还是学术界大家都在惊叹一个又一个的模型设计。但是对于真正做过算法工程落地的同学,在惊叹这些模型的同时,更多的是在忧虑如…...
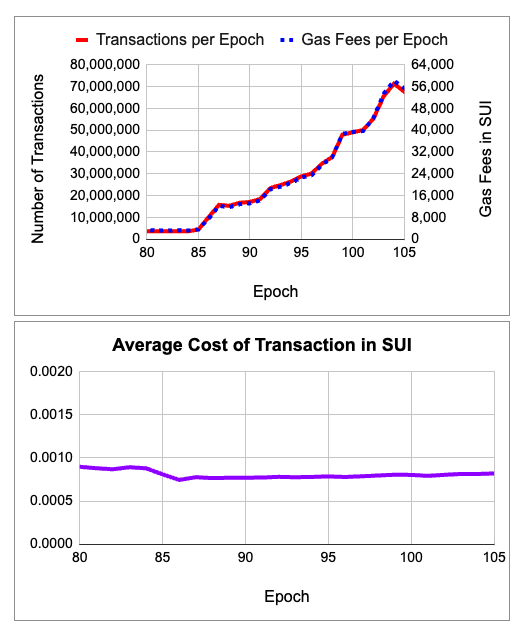
Sui网络的稳定性和高性能
Sui的最初的协议开发者设计了可扩展的网络,通过水平扩展的方式来保持可负担得起的gas费用。其他区块链与之相比,则使用稀缺性和交易成本来控制网络活动。 Sui主网上线前90天的数据指标证明了这一设计概念,在保持100%正常运行的同…...
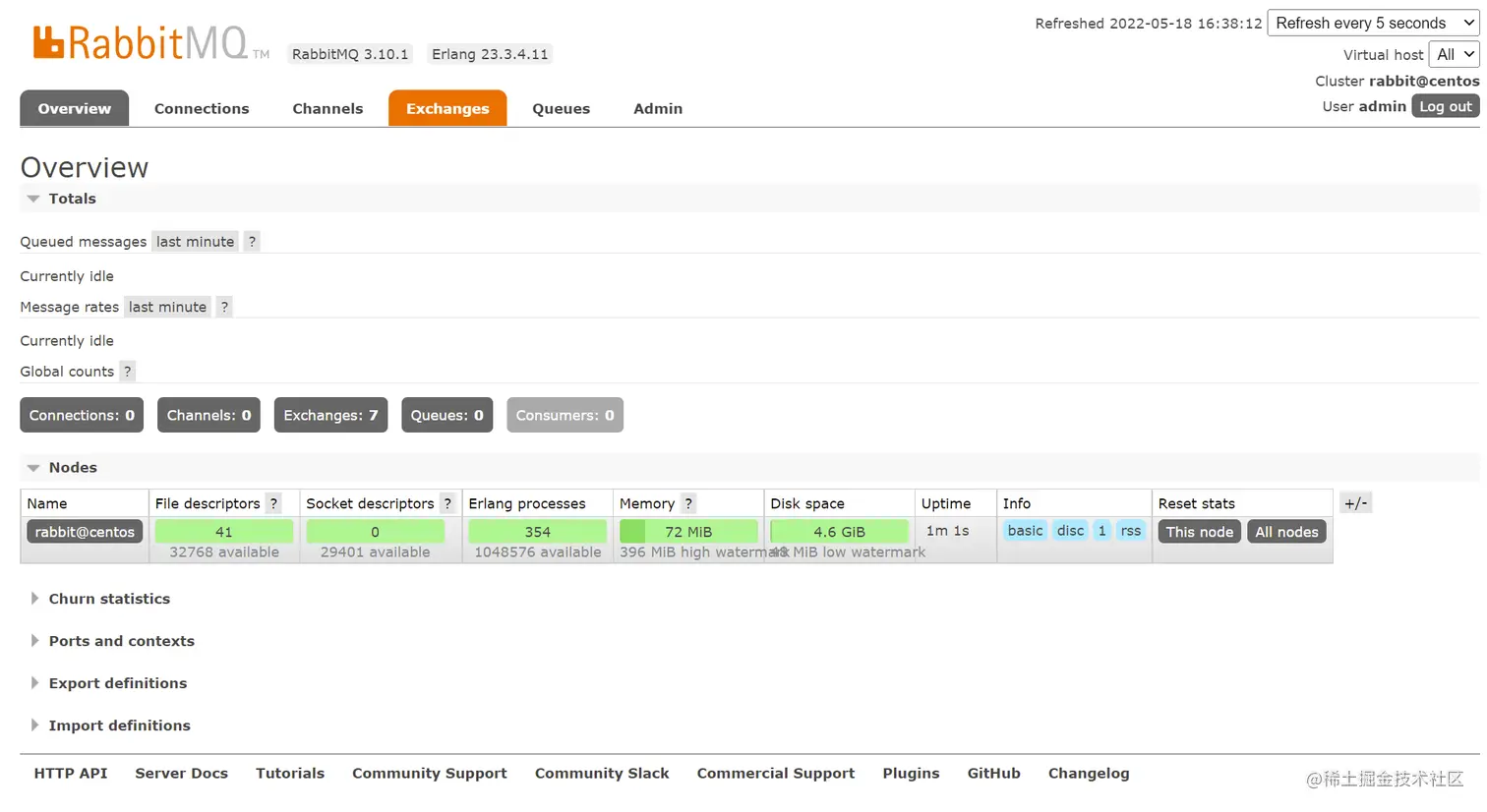
RabbitMQ 安装教程
RabbitMQ 安装教程 特殊说明 因为RabbitMQ基于Erlang开发,所以安装时需要先安装Erlang RabbitMQ和Erlang版本对应关系 查看地址:www.rabbitmq.com/which-erlan… 环境选择 Erlang: 23.3及以上 RabbitMQ: 3.10.1Windows 安装 1. 安装Erlang 下载地…...

STM32F429IGT6使用CubeMX配置GPIO点亮LED灯
1、硬件电路 2、设置RCC,选择高速外部时钟HSE,时钟设置为180MHz 3、配置GPIO引脚 4、生成工程配置 5、部分代码 6、实验现象...

DOM的节点操作+事件高级+DOM事件流+事件对象
一.节点操作 1.父节点: node.parentNode 得到的是离元素最近的父级节点 2.子节点: parentNode.childNodes 所有的子节点 包含元素节点 文本节点等等parentNode.children (非标准) 获取所有的子元素节点,实际开发常用 parentNode.firstChild 获取…...
云端剪切板,让你的数据同步无界
云端剪切板,让你的数据同步无界! 每个人都应该保护自己的数据,同时使它易于访问和共享。这就是我们的云剪切板网站诞生的原因!无论你在哪里,只要登录我们的网站,就可以随时随地使用你的剪切板数据。 你可…...

Location匹配与Rewrite重写
一、常见的Nginx正则表达式 ^ :匹配输入字符串的起始位置 $ :匹配输入字符串的结束位置 * :匹配前面的字符零次或多次。如“ol*”能匹配“o”及“ol”、“oll”:匹配前面的字符一次或多次。如“ol”能匹配“ol”及“oll”、“oll…...
Docker源码阅读 - goland环境准备
docker 源码分为两部分 cli 和 moby(docker) tips: docker是从moby拷贝过去的;docker整体是一个C-S架构,cli客户端,docker服务端 docker-ce:https://github.com/docker/docker-ce cli:https://…...

数据库信息速递 -- MariaDB 裁员后,前景不确定 (翻译)
开头还是介绍一下群,如果感兴趣polardb ,mongodb ,mysql ,postgresql ,redis 等有问题,有需求都可以加群群内有各大数据库行业大咖,CTO,可以解决你的问题。加群请加 liuaustin3微信号 ,在新加的朋友会分到3群ÿ…...

4.1 Windows终端安全
数据参考:CISP官方 目录 安全安装保护账户安全本地安全策略安全中心系统服务安全其他安全设置软件安全获取 一、安全安装(以安装windows系统为例) 选择合适的版本 商业版本:家庭版、专业版、专业工作站版、企业版特殊版本&…...
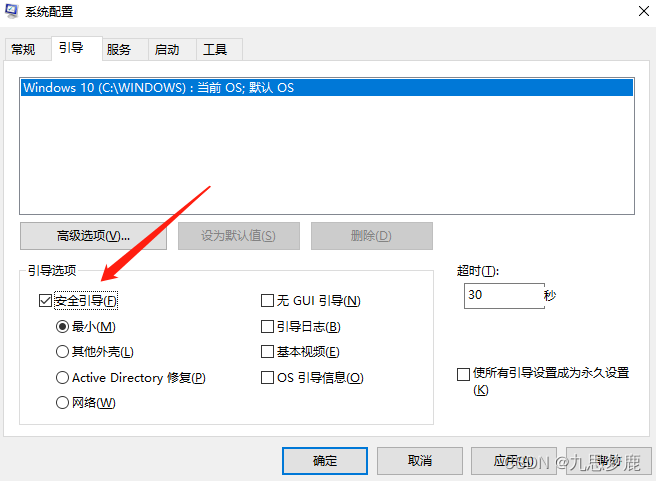
win10强制卸载奇安信天擎
1、win r 打开运行 2、输入msconfig进入系统配置面板 3、点击引导,修改安全引导配置项 4、重启系统(桌面会变成纯黑背景,符合预期,莫紧张) 5、删除安装的文件夹 若是安装天擎时选择的自定义安装,则配置…...

npm常用命令
npm -v:查看 npm 版本 npm init:初始化后会出现一个 Package.json 配置文件,可以在后面加上 -y,快速跳到问答界面 npm install:会根据项目中的 package.json 文件自动给下载项目中所需的全部依赖 npm insall 包含 -…...
创建型设计模式:4、原型模式(Prototype Pattern))
(一)创建型设计模式:4、原型模式(Prototype Pattern)
目录 1、原型模式的含义 2、C实现原型模式的简单实例 1、原型模式的含义 通过复制现有对象来创建新对象,而无需依赖于显式的构造函数或工厂方法,同时又能保证性能。 The prototype pattern is a creational design pattern in software development. …...
【算法学习】高级班九
这种互为旋变串: 给定两个字符串,判断是否互为旋变串 代码: 打表法: 每一层内的数字不互相依赖,只依赖它下面的层但实际上size会约束L1和L2的值,即L1和L2<N-size 思路:设置一个窗口…...
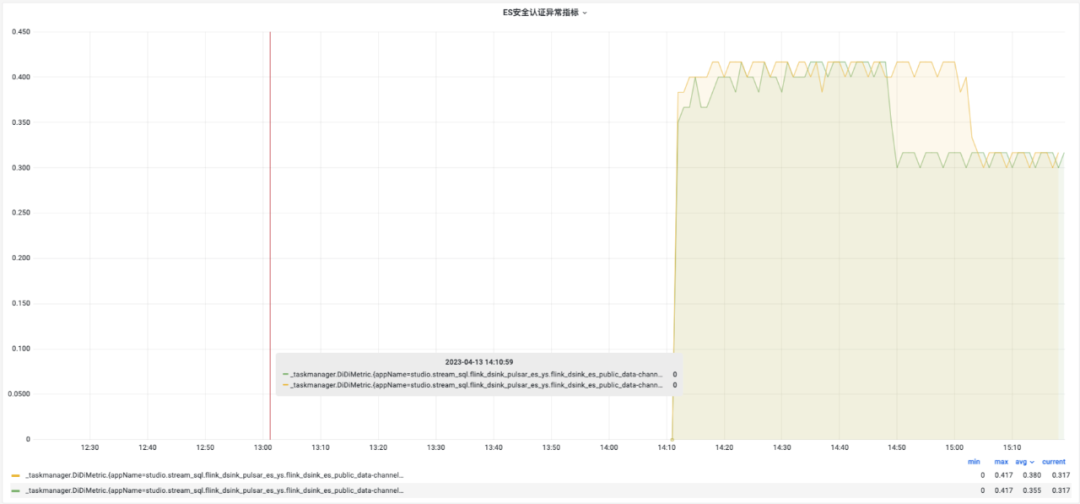
数据安全加固:深入解析滴滴ES安全认证技术方案
前文分别介绍了滴滴自研的ES强一致性多活是如何实现的、以及如何提升ES的性能潜力。由于ES具有强大的搜索和分析功能,同时也因其开源和易于使用而成为黑客攻击的目标。近些年,业界ES数据泄露事件频发, 以下是一些比较严重的数据泄露案件: 202…...

Typescript第九/十章 前后端框架,命名空间和模块
第九章 前后端框架 9.1 前端框架 Typescript特别适合用于开发前端应用。Typescript对JSX有很好的支持,而且能安全地建模不可变性,从而提升应用的结构和安全性,写出的代码正确性高,便于维护。 9.1.1 React JSX/TSX内容等 详情…...

LLM - argparse 解析脚本参数
目录 一.引言 二.argparse 解析 shell 参数 1.使用步骤 2.python 侧示例 3.shell 侧示例 一.引言 CUDA_VISIBLE_DEVICES0 python src/train_bash.py \--stage pt \--model_name_or_path path_to_your_model \--do_train \--dataset wiki_demo \--template default \--fin…...

谈一谈在两个商业项目中使用MVI架构后的感悟
作者:leobertlan 前言 当时项目采用MVP分层设计,组员的代码风格差异也较大,代码中类职责赋予与封装风格各成一套,随着业务急速膨胀,代码越发混乱。试图用 MVI架构 单向流 形成 掣肘 带来一致风格。 但这种做法不够以…...

ApacheCon - 云原生大数据上的 Apache 项目实践
Apache 软件基金会的官方全球系列大会 CommunityOverCode Asia(原 ApacheCon Asia)首次中国线下峰会将于 2023 年 8 月 18-20 日在北京丽亭华苑酒店举办,大会含 17 个论坛方向、上百个前沿议题。 字节跳动云原生计算团队在此次 CommunityOve…...

DAY 47
三、通道注意力 3.1 通道注意力的定义 # 新增:通道注意力模块(SE模块) class ChannelAttention(nn.Module):"""通道注意力模块(Squeeze-and-Excitation)"""def __init__(self, in_channels, reduction_rat…...

为什么需要建设工程项目管理?工程项目管理有哪些亮点功能?
在建筑行业,项目管理的重要性不言而喻。随着工程规模的扩大、技术复杂度的提升,传统的管理模式已经难以满足现代工程的需求。过去,许多企业依赖手工记录、口头沟通和分散的信息管理,导致效率低下、成本失控、风险频发。例如&#…...

[ICLR 2022]How Much Can CLIP Benefit Vision-and-Language Tasks?
论文网址:pdf 英文是纯手打的!论文原文的summarizing and paraphrasing。可能会出现难以避免的拼写错误和语法错误,若有发现欢迎评论指正!文章偏向于笔记,谨慎食用 目录 1. 心得 2. 论文逐段精读 2.1. Abstract 2…...

Java面试专项一-准备篇
一、企业简历筛选规则 一般企业的简历筛选流程:首先由HR先筛选一部分简历后,在将简历给到对应的项目负责人后再进行下一步的操作。 HR如何筛选简历 例如:Boss直聘(招聘方平台) 直接按照条件进行筛选 例如:…...

学习STC51单片机32(芯片为STC89C52RCRC)OLED显示屏2
每日一言 今天的每一份坚持,都是在为未来积攒底气。 案例:OLED显示一个A 这边观察到一个点,怎么雪花了就是都是乱七八糟的占满了屏幕。。 解释 : 如果代码里信号切换太快(比如 SDA 刚变,SCL 立刻变&#…...

Kafka入门-生产者
生产者 生产者发送流程: 延迟时间为0ms时,也就意味着每当有数据就会直接发送 异步发送API 异步发送和同步发送的不同在于:异步发送不需要等待结果,同步发送必须等待结果才能进行下一步发送。 普通异步发送 首先导入所需的k…...
)
GitHub 趋势日报 (2025年06月06日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 590 cognee 551 onlook 399 project-based-learning 348 build-your-own-x 320 ne…...

Web中间件--tomcat学习
Web中间件–tomcat Java虚拟机详解 什么是JAVA虚拟机 Java虚拟机是一个抽象的计算机,它可以执行Java字节码。Java虚拟机是Java平台的一部分,Java平台由Java语言、Java API和Java虚拟机组成。Java虚拟机的主要作用是将Java字节码转换为机器代码&#x…...

【Linux手册】探秘系统世界:从用户交互到硬件底层的全链路工作之旅
目录 前言 操作系统与驱动程序 是什么,为什么 怎么做 system call 用户操作接口 总结 前言 日常生活中,我们在使用电子设备时,我们所输入执行的每一条指令最终大多都会作用到硬件上,比如下载一款软件最终会下载到硬盘上&am…...

《信号与系统》第 6 章 信号与系统的时域和频域特性
目录 6.0 引言 6.1 傅里叶变换的模和相位表示 6.2 线性时不变系统频率响应的模和相位表示 6.2.1 线性与非线性相位 6.2.2 群时延 6.2.3 对数模和相位图 6.3 理想频率选择性滤波器的时域特性 6.4 非理想滤波器的时域和频域特性讨论 6.5 一阶与二阶连续时间系统 6.5.1 …...
