当前位置： 首页 > news >正文

CentOS根分区扩容实战（非LVM）！

news 2025/6/4 14:32:26

  1. 在虚拟化平台（如KVM,ESXI）中，将虚拟机的磁盘大小扩展到所需的大小。这将增加虚拟机的磁盘空间。

  2. 在虚拟机中，使用以下命令查看可用的磁盘和分区信息：

    sudo fdisk -l

  3. 确定要扩展的根分区的设备名称（如 /dev/sda1）。

  4. 安装 gdisk 工具（如果未安装）：

    sudo yum install gdisk

  5. 运行以下命令来扩展分区：

    sudo gdisk /dev/sda

    这将打开 gdisk 工具并加载 /dev/sda 设备的分区表。

  6. 在 gdisk 提示符下，输入 p 查看分区表。

  7. 记下根分区（例如 /dev/sda1）的起始扇区号,一般默认为2048。

  8. 输入 d 删除根分区。

  9. 输入 n 创建一个新的主分区。

  10. 提示输入分区号，按回车键使用默认值。

  11. 提示输入起始扇区号，输入之前记下的起始扇区号。

  12. 提示输入结束扇区号，按回车键使用默认值，以使用整个可用空间。

  13. 输入 t 设置分区类型。

  14. 提示输入分区号，按回车键使用默认值。

  15. 提示输入分区类型代码，输入 8e00 表示 Linux LVM 分区。

  16. 输入 w 保存更改并退出 gdisk。

  17. 运行以下命令来重新加载分区表：

    partprobe

  18. 刷新文件系统

xfs_growfs /dev/sda

相关文章：

CentOS根分区扩容实战（非LVM）！

在虚拟化平台（如KVM,ESXI）中，将虚拟机的磁盘大小扩展到所需的大小。这将增加虚拟机的磁盘空间。 在虚拟机中，使用以下命令查看可用的磁盘和分区信息： sudo fdisk -l确定要扩展的根分区的设备名称（如 /dev/…...

编程日记 2023/8/12 6:35:23

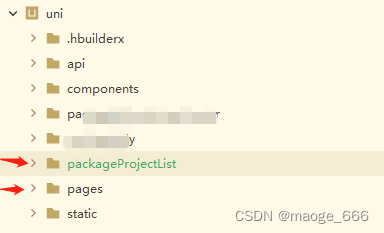
uniapp 微信小程序 分包

1、manifest.json内添加如图所示： "optimization" : {"subPackages" : true },2、在与pages同级上创建各个分包的文件夹 把需要分包的文件对应移入分包文件夹内 3、page.json内修改分包文件的路径 比如： {"path" : &qu…...

编程日记 2023/8/12 6:34:22

Redis_安装、启动以及基本命令

2.Redis安装 2.1前置处理环境 VMware安装安装centOS的linux操作系统xshellxftp 2.2 配置虚拟机网络 按ctrlaltf2 切换到命令行 cd (/)目录 修改/etc/sysconfig/network-scripts/ifcfg-ens3 vi 命令 按insert表示插入 按ctrlesc退出修改状态 :wq 写入并退出 此文件必须保持一…...

编程日记 2023/8/12 6:33:22

IPv4编址及子网划分

IPv4编址及子网划分 一、IPv4地址概述1.1、IPv4报文结构1.2、IPv4地址分类1.2.1、A类1.2.2、B类1.2.3、C类1.2.4、D类1.2.5、E类 1.3、私有IP地址1.4、特殊地址 二、子网划分2.1、子网掩码2.2、VLSM 可变长的子网掩码2.3、子网划分2.4、子网划分示例2.4.1、子网划分案例 —— A…...

编程日记 2023/8/12 6:32:20

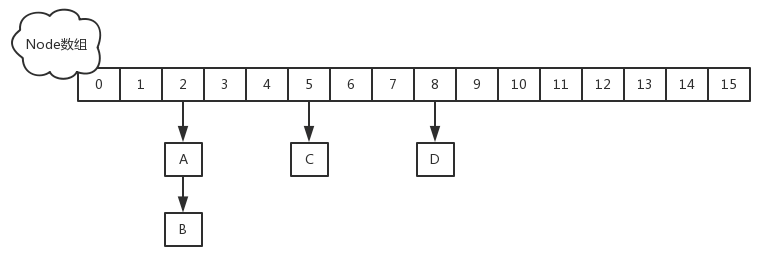
HashMap 二十一问

1&#xff1a;HashMap 的数据结构&#xff1f; A&#xff1a;哈希表结构&#xff08;链表散列&#xff1a;数组链表&#xff09;实现&#xff0c;结合数组和链表的优点。当链表长度超过 8 时&#xff0c;链表转换为红黑树。transient Node<K,V>[] table; 2&#xff1a;…...

编程日记 2023/8/12 6:31:19

什么是Selenium？使用Selenium进行自动化测试

什么是 Selenium&#xff1f;   Selenium 是一种开源工具&#xff0c;用于在 Web 浏览器上执行自动化测试&#xff08;使用任何 Web 浏览器进行 Web 应用程序测试&#xff09;。   等等&#xff0c;先别激动&#xff0c;让我再次重申一下&#xff0c;Selenium 仅可以测试We…...

编程日记 2023/8/12 6:30:18

解决“先commit再pull”造成的git冲突

一、问题场景 在分支上修改了代码然后commit&#xff08;没有push&#xff09;&#xff0c;此时再git pull&#xff0c;拉下了别人的修改&#xff0c;但是报错无法merge 二、解决步骤 1.在idea下方工具栏选择git -> log&#xff0c;可以看到版本变化链表&#xff0c;右键…...

编程日记 2023/8/12 6:29:17

JAVA设计模式----原型设计模式

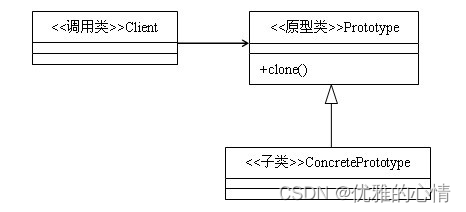
文章目录 一、简介二、实现方式三、原型模式的注意事项浅拷贝与深拷贝浅拷贝深拷贝一、简介 定义：用原型实例指定创建对象的种类，并通过拷贝这些原型创建新的对象。 类型：创建类模式 类图： 原型模式主要用于对象的复制，它的核心是就是类图中的原型类Prototype。Protot…...

编程日记 2023/8/12 6:28:16

树·c++

树&#xff08;Tree&#xff09; 是一种非线性的数据结构&#xff0c;它由若干个 节点&#xff08;Node&#xff09; 组成&#xff0c;并通过 边&#xff08;Edge&#xff09; 相互连接。树的结构类似于现实中的树&#xff0c;其中 根节点&#xff08;Root Node&#xff09; 位…...

编程日记 2023/8/12 6:27:15

vuejs 设计与实现 - 双端diff算法

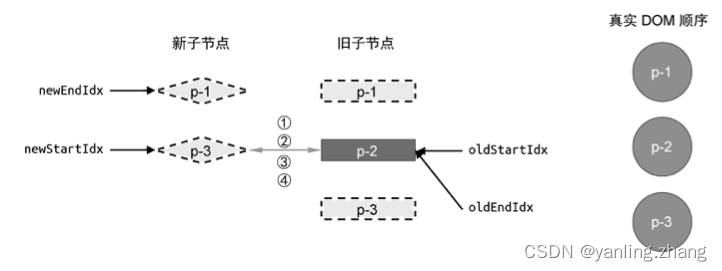
我们介绍了简单 Diff 算法的实现原理。简单 Diff 算法利用虚拟节点的 key 属性&#xff0c;尽可能地复用 DOM元素&#xff0c;并通过移动 DOM的方式来完成更新&#xff0c;从而减少不断地创建和销毁 DOM 元素带来的性能开销。但是&#xff0c;简单 Diff 算法仍然存在很多缺陷&a…...

编程日记 2023/8/12 6:26:13

RISC-V在快速发展的处理器生态系统中找到立足点

原文&#xff1a;RISC-V Finds Its Foothold in a Rapidly Evolving Processor Ecosystem 作者&#xff1a;Agam Shah 转载自&#xff1a;https://thenewstack.io/risc-v-finds-its-foothold-in-a-rapidly-evolving-processor-ecosystem/ 以下是正文 But the open source pr…...

编程日记 2023/8/12 6:25:12

面试题02

这里写目录标题 主存储器和CPU之间增加Cache的目的是？判断一个char变量c1是否为小写字母循环链表顺序存储的线性表，访问结点和增加删除结点的时间复杂度请列举你所知道的c/c++ 语言中引入性能开销或阻碍编译优化的语言特性，并尝试说明对应的解决办法请列举CPU cache对编程开…...

编程日记 2023/8/12 6:24:11

第六章 SpringBoot注解 @ConditionalOnBean

满足条件的则进行组件的注入 Configuration(proxyBeanMethods true) //告诉SpringBoot这是一个配置类 配置文件 ConditionalOnBean(name "tom") public class MyConfig {Bean("tom")public Pet tom(){return new Pet("tomPet");}/*** 外部无论…...

编程日记 2023/8/12 6:23:10

MySQL8的下载与安装-MySQL8知识详解

本文的内容是mysql8的下载与安装。主要讲的是两点&#xff1a;从官方网站下载MySQL8安装和从集成环境安装MySQL8。 一、从官方网站下载MySQL8.0安装 MySQL8.0官方下载地址是&#xff1a;&#xff08;见图&#xff09; 官方正式版的最新版本是8.0.34&#xff0c;也推出了创新版…...

编程日记 2023/8/12 6:22:09

ATF(TF-A)安全通告 TFV-9 (CVE-2022-23960)

ATF(TF-A)安全通告汇总 目录 一、ATF(TF-A)安全通告 TFV-9 (CVE-2022-23960) 二、CVE-2022-23960 一、ATF(TF-A)安全通告 TFV-9 (CVE-2022-23960) Title TF-A披露通过分支预测目标重用&#xff08;branch prediction target reuse&#xff09;引发的前瞻执行处理器漏洞 CV…...

编程日记 2023/8/12 6:21:08

docker实现Nginx

文章目录 1.docker 安装2.docker环境实现Nginx 1.docker 安装 1.使用环境为红帽8.1,添加源 yum-config-manager --add-repo https://mirrors.aliyun.com/docker-ce/linux/centos/docker-ce.repo2.安装 yum install docker-ce docker-ce-cli containerd.io显示出错 Docker C…...

编程日记 2023/8/12 6:20:07

【Java 回忆录】Java全栈开发笔记文档

这里能学到什么&#xff1f; 实战代码文档一比一记录实战问题和解决方案涉及前端、后端、服务器、运维、测试各方面通过各方面的文档与代码&#xff0c;封装一套低代码开发平台直接开腾讯会议&#xff0c;实实在线一起分享技术问题核心以 Spring Boot 作为基础框架进行整合后期…...

编程日记 2023/8/12 6:19:04

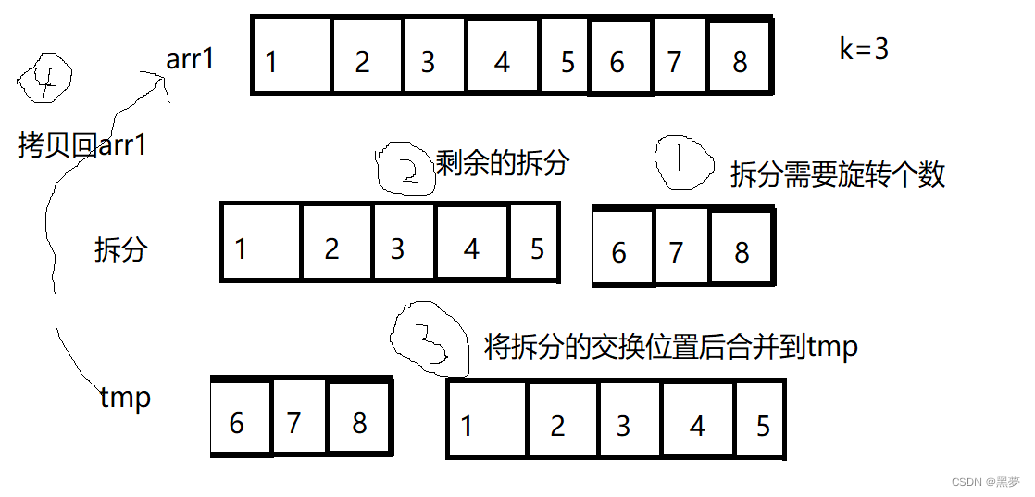
数据结构：力扣刷题

题一&#xff1a;旋转数组 给定一个整数数组 nums&#xff0c;将数组中的元素向右轮转 k 个位置&#xff0c;其中 k 是非负数。 思路一&#xff1a; 创建reverse()函数传入三个值分别为数组地址&#xff0c;从第几个数组元素开始&#xff0c;结束元素位置&#xff1b; 在r…...

编程日记 2023/8/12 6:18:04

【Java】常用设计模式的理解

设计模式 前言 有一些重要的设计原则在开篇和大家分享下&#xff0c;这些原则将贯通全文&#xff1a; 面向接口编程&#xff0c;而不是面向实现。这个很重要&#xff0c;也是优雅的、可扩展的代码的第一步&#xff0c;这就不需要多说了吧。 职责单一原则。每个类都应该只有一…...

编程日记 2023/8/12 6:17:03

python - 爬虫简介

什么是爬虫&#xff1f; 模拟浏览器对网站服务器发送请求解析服务器返回的响应数据&#xff0c;并保存数据 爬虫能获取哪些数据&#xff1f; 原则上所有可以通过浏览器获取的数据都可以爬取爬虫也只能获取爬取浏览器可以正常获取的数据 爬虫的应用场景&#xff1f; 数据分…...

编程日记 2023/8/12 6:16:02

Java 中执行命令并使用指定配置文件的最佳实践

在Java开发中&#xff0c;有时需要从Java应用程序中执行系统命令&#xff0c;并使用指定的配置文件来控制这些命令的行为。本文将详细介绍在Java中执行命令并使用指定配置文件的最佳实践&#xff0c;包括如何设置环境变量、重定向输入输出以及处理可能出现的异常。 一、基本实…...

编程新知 2025/6/4 13:42:07

基于springboot的益智游戏系统的设计与实现

博主介绍&#xff1a;java高级开发&#xff0c;从事互联网行业六年&#xff0c;熟悉各种主流语言&#xff0c;精通java、python、php、爬虫、web开发&#xff0c;已经做了六年的毕业设计程序开发&#xff0c;开发过上千套毕业设计程序&#xff0c;没有什么华丽的语言&#xff0…...

编程新知 2025/6/4 12:57:58

深度强化学习赋能城市消防优化，中科院团队提出DRL新方法破解设施配置难题

在城市建设与发展中&#xff0c;地理空间优化至关重要。从工业园区选址&#xff0c;到公共服务设施布局&#xff0c;它都发挥着关键作用。但传统求解方法存在诸多局限&#xff0c;如今&#xff0c;深度学习技术为其带来了新的转机。 近日&#xff0c;在中国地理学会地理模型与…...

编程新知 2025/6/4 9:13:54

【C++高并发内存池篇】性能卷王养成记：C++ 定长内存池，让内存分配快到飞起！

&#x1f4dd;本篇摘要 在本篇将介绍C定长内存池的概念及实现问题&#xff0c;引入内存池技术&#xff0c;通过实现一个简单的定长内存池部分&#xff0c;体会奥妙所在&#xff0c;进而为之后实现整体的内存池做铺垫&#xff01; &#x1f3e0;欢迎拜访&#x1f3e0;&#xff…...

编程新知 2025/6/4 5:13:44

清理 pycharm 无效解释器

1. 起因&#xff0c; 目的: 经常使用 pycharm 来调试深度学习项目&#xff0c;每次新建虚拟环境&#xff0c;都是显示一堆不存在的名称&#xff0c;删也删不掉。 总觉得很烦&#xff0c;是个痛点。决定深入研究一下。 2. 先看效果 效果是能行&#xff0c;而且清爽多了。 3. …...

编程新知 2025/6/4 3:41:21

宁夏农业科技：创新引领，赋能现代农业新篇章

在广袤的宁夏大地上&#xff0c;农业科技如同一股强劲的春风&#xff0c;吹拂着每一寸土地&#xff0c;为宁夏的农业发展注入了新的活力与希望。近年来&#xff0c;宁夏农业科技以其独特的创新力和实践力&#xff0c;不断推动着现代农业的转型升级&#xff0c;让这片古老的土地…...

编程新知 2025/6/3 23:03:41

【保姆级教程】PDF批量转图文笔记

如果你有一个PDF文档&#xff0c;然后你想把它发成图文笔记emmm&#xff0c;最好再加个水印&#xff0c;你会怎么做&#xff1f; 其实也不麻烦&#xff0c;打开PDF文档&#xff0c;挨个截图&#xff0c;然后打开PS一张一张图片拖进去&#xff0c;再把水印图片拖进去&#xff0…...

编程新知 2025/6/3 22:58:26

AWS API Gateway 配置WAF（中国区）

问题 需要给AWS API Gateway配置WAF。 AWS WAF设置 打开AWS WAF首页&#xff0c;开始创建和配置WAF&#xff0c;如下图&#xff1a; 设置web acl名称&#xff0c;然后开始添加aws相关资源&#xff0c;如下图&#xff1a; 选择资源类型&#xff0c;但是&#xff0c;我这里出…...

编程新知 2025/6/3 22:16:26

Java设计模式详解：策略模式（Strategy Pattern）

在软件开发中&#xff0c;设计模式是解决常见问题的经典方法。策略模式&#xff08;Strategy Pattern&#xff09;作为一种行为型设计模式&#xff0c;能够将算法或行为的定义与使用分离&#xff0c;使得算法可以独立于客户端代码进行变化和扩展。本文将深入解析策略模式的核心…...

编程新知 2025/6/3 18:50:14

力扣刷题Day 68：搜索插入位置（35）

1.题目描述 2.思路 方法1&#xff1a;回溯的二分查找。 方法2&#xff1a;看到了一个佬很简洁的写法&#xff0c;代码贴在下面了。 3.代码&#xff08;Python3&#xff09; 方法1&#xff1a; class Solution:def searchInsert(self, nums: List[int], target: int) ->…...

编程新知 2025/6/3 17:36:24