oi知识表+NOIP提高组算法及算法思想总结

算法及算法思想总结
│ By lib
│
├暴力
├模拟
├递归及递推:数位统计类
├构造
▼├排序算法
│ ├冒泡排序
│ ├选择排序
│ ├计数排序
│ ├基数排序
│ ├插入排序
│ ├归并排序
│ ├快速排序
│ ├堆排序
│ └二叉排序树
│
▼├分治
│ ├快速幂
│ ├单调区间求解(二分答案再验证)
│ ├二分后,先各自计算,然后再根据某种策略合并答案
│ ├逆序对统计
│
▼├贪心
│ ├不相交区间、区间选点问题、区间覆盖问题
│ ├流水作业调度问题、带期限和罚款的单位时间任务调度问题
│ ├其它最优化问题
│
▼├搜索
│ ▼├剪枝
│ │ ├最优化剪枝(可先贪心一个次优解)
│ │ ├可行性
│ │
│ ▼├深度优先搜索(dfs):网格数据
│ │ ▼├实现方式
│ │ │ ├递归实现(栈<=10000-20000层)
│ │ │ └非递归实现(手动栈)
│ │ │
│ │ ├贪心:预处理路径
│ │ ├回溯法
│ │
│ ▼├广度优先搜索(bfs):线性数据
│ │ ├队列(先进先出)
│ │ └双向广度优先搜索(从源汇点同时搜)
│ │
│ ├FloodFill(种子填充法)
│ ├搜索顺序
│ ├搜索与其他算法结合
│ ├二分检索
│
▼├规划
│ ▼├动态规划(DP)
│ │ ▼├优化
│ │ │ ├数据结构
│ │ │ ├单调队列
│ │ │
│ │ ├背包(背包九讲)
│ │ ├区间型动态规划
│ │ ├子序列型动态规划
│ │ ├环形动态规划
│ │ ├树形动态规划
│ │ ├字符串型动态规划
│ │ └记忆化搜索
│ │
│
▼├图论
│ ▼├基本概念
│ │ ├简单路径:一条路径上的结点除起点x1和终点xk可以相同外,其它结点均不相同(x1=xk的简单路径称为回路/环)
│ │ ├阶(图结点个数),度=入度+出度(奇点和偶点)
│ │ ├带权图称为网
│ │ ├子图:假设有两个图G=(V,E)和G’=(V’,E’),如果V’∈ V且E’∈ E,则称G’为G的子图。
│ │ ├连通分量:极大连通子图
│ │ ├混合图(有向+无向):“()”无向边;“<>”有向边
│ │ ├邻接边,邻接点
│ │ ├简单图(无环),完全图(点与点之间均有边)
│ │ ├迹(无重复边),通路/轨(无重复点),圈(起点和终点重合的轨)
│ │ ├DAG(有向无环图)
│ │
│ ├拓扑序(关键路径):AOV网
│ ▼├最短路(三角不等式)
│ │ ▼├算法
│ │ │ ▼├单源最短路(SSSP)
│ │ │ │ ├Dijkstra(无法处理负环)(堆优化) O(n^2) {O(E lg V)}
│ │ │ │ ▼└Spfa(堆优化) O(kE)
│ │ │ │ ├Bellman-Ford的变形
│ │ │ │ └松弛操作
│ │ │ │
│ │ │ ▼└所有顶点对间最短路(APSP)
│ │ │ ├Floyd:在最外层循环做了k-1次之后,dist[i][j]则代表了i到j的路径中,所有结点编号都小于k的最短路径。
│ │ │
│ │ ├次短路∈前K短路
│ │
│ ▼├(最小)生成树(MST)
│ │ ▼├无向图最小生成树
│ │ │ ├Prim(堆优化) O(V^2+E) {O((V+E) lg V)}
│ │ │ └Kruskal(并查集优化) O(E lg E+V*E) {O(E lg E+Eα(V))}
│ │
│ │
│ ▼├网络流
│ │ ▼├算法
│ │ │ ▼├增广路算法
│ │ │ │ ▼├Ford-Fulkerson方法
│ │ │ │ │ ├Edmonds-Karp算法(bfs) O(V*E^2)
│ │ │ │ │ └dfs(效率低下)
│ │ │ │ │
│ │ │ │ ▼└最短增广路算法(分层图) O(V^2*E)
│ │ │ │ ├最短路径增值(MPLA)
│ │ │ │ ├Sap(Gap优化) 推荐
│ │ │ │ └Dinic
│ │ │ │
│ │ │ ▼├预流推进算法:
│ │ │ │ ├push-relabel算法 O(V^2*E)
│ │ │ │ ├relabel-to-front算法 O(V^3)
│ │ │ │ └Hlpp(最高标号预流推进算法)(效率高但代码长) O(V^2*sqrt(E))
│ │ │ │
│ │ │ └压入与重标记算法
│ │
│ ▼├路径
│ │ ├哈密顿回路:点
│ │ └欧拉回路:边(欧拉图:含欧拉回路)
│ │
│ │
│ ├dfs序,bfs序的使用
│
▼├离散结构
│ ▼├串、树
│ │ ├LCA与RMQ相互转化
│ │
│ ▼├矩阵
│ │ ├部分和(前缀和)
│ │ ├离散化
│ │
│
│
▼├数据结构
│ ├顺序表:数组
│ ▼├链表
│ │ ▼├单链表
│ │ ├双链表
│ │ ├循环链表
│ │
│ ├串(见离散结构)
│ ▼├集合
│ │ ▼├哈希表(散列表)
│ │ │ ▼├哈希函数
│ │ │ │ ├直接定址法
│ │ │ │ ├数字分析法
│ │ │ │ ├平方取中法
│ │ │ │ └折叠法
│ │ │ │
│ │ │ ├分段Hash
│ │ │ ▼└处理冲突
│ │ │ ├拉链法
│ │ │ ├多哈希法
│ │ │ ├开放地址法
│ │ │ └建域法
│ │ │
│ │ └并查集(路径压缩)
│ │
│ ▼├堆
│ │ ▼├二叉堆
│ │ │ └最大-最小堆
│ │ │
│ │
│ ├栈:手写栈
│ ▼├队列
│ │ ├链队列
│ │ ├循环队列
│ │ ▼└优先队列(带权值的队列)
│ │
│ ▼├树
│ │ ▼├线段树
│ │ │ └Lazy标记
│ │ │
│ │ ├树状数组(在线支持修改的前缀和)
│ │
│ ▼└图的表示
│ ├邻接矩阵
│ ├邻接表
│ └链式前向星
│
▼├数学
│ ├高精度(*高精除高精不要求*)
│ ├排列组合:Stirling数
│ ├二项式定理
│ ├康托展开:一个全排列到一个整数的双射,经常用来做可以用全排列表示状态的搜索的哈希函数
│ ▼├组合计数
│ │ ▼├递推关系与生成函数(母函数)
│ │ │ ├普通型母函数
│ │ │ └指数型母函数:Fibonacci数列,Catalan数列
│ │ │
│ │ ├抽屉原理
│ │ ├容斥原理
│ │
│ ├素数及素数判定
│ ├乘法逆元(可用欧拉定理,扩展欧几里德定理求解):若ax≡1(mod f),则称a关于模f的乘法逆元为x。
│ ▼├最大公约数
│ │ ├欧几里德算法(辗转相除法):gcd(a,b)=gcd(b,a mod b)
│ │ └扩展欧几里德定理:存在唯一的整数 x,y 使得gcd(a,b)=ax+by
│ │
│
做题流程:1、建模(脱马甲);2、破冰(有序、单调、逆向,发散)(状态与状态间联系);3、设计数据结构保存相关信息,并在数据结构的基础上设计算法解决问题(要证明);4、编写代码、调试程序。
每题任务:1、你尝试了几个解题方向和思路?2、正解怎么做的?3、怎样从题目到正解?4、你自己目标分多少?有没有达到?
理科生做题,多问自己为什么要这么做,下次遇到类似的问题怎么办?
相关文章:

oi知识表+NOIP提高组算法及算法思想总结
算法及算法思想总结 │ By lib │ ├暴力 ├模拟 ├递归及递推:数位统计类 ├构造 ▼├排序算法 │ ├冒泡排序 │ ├选择排序 │ ├计数排序 │ ├基数排序 │ ├插入排序 │ ├归并排序 │ ├快速排序 │…...
【mysql】实现递归查询
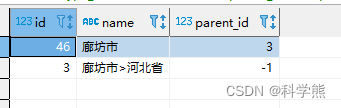
mysql实现递归查询的方法:首先创建表,并初始化数据;然后向下递归,利用find_in_set()函数和group_concat()函数、with recursive实现递归查询。 mysql实现递归查询的方法: 1、创建表 DROP TABLE IF EXISTS t_areainf…...

JUC并发编程之原子类
目录 1. 什么是原子操作 1.1 原子类的作用 1.2 原子类的常见操作 原子类的使用注意事项 并发编程是现代计算机应用中不可或缺的一部分,而在并发编程中,处理共享资源的并发访问是一个重要的问题。为了避免多线程访问共享资源时出现竞态条件࿰…...

测试设计中隐藏的边界有哪些?
概述:边界值分析是测试设计一个稳定的部分,但是对黑盒测试人员来讲有时候边界并不是那么明显。这些不明显的边界被称作隐藏的边界。本文提供几个隐藏的边界的例子,还有一些以让隐藏边界显露来设计测试计划的要点方法。 使用边界值分析和等价…...

领航优配:暑期旅游市场热度持续攀升,相关公司业绩有望持续释放
到发稿,海看股份涨停,中广天择、探路者、众信旅行等涨幅居前。 8月8日,在线旅行板块震动上涨,到发稿,海看股份涨停,中广天择、探路者、众信旅行等涨幅居前。 今年以来,国内旅行商场逐渐恢复。文…...

基于 CentOS 7 构建 LVS-DR 集群 及 配置nginx负载均衡
一、构建LVS-DR集群 1、主机规划 Node01:PC Node02:LVS Node03、Node04:Webserver 2、部署环境 2.1 在Node02上配置 2.1.1 安装ipvsadm管理软件按 [rootlocalhost ~]# yum install -y ipvsadm 2.1.2 配置VIP [rootlocalhost ~]# if…...

docker搭建在线Markdown服务器
1.安装docker 2.编写docker-compose.yml version: "3" services:database:image: postgres:11.6-alpineenvironment:- POSTGRES_USERcodimd- POSTGRES_PASSWORDchange_password- POSTGRES_DBcodimdvolumes:- "database-data:/var/lib/postgresql/data"re…...

打靶练习:WestWild 1.1(一个简单但不失优雅的Ubuntu靶机)
主机发现和nmap信息收集 //主机发现 sudo nmap -sn 192.168.226.0/24 //扫描整个C段//端口扫描//初步扫描 sudo nmap -sT --min-rate 10000 -p- 192.168.226.131 -oA nmapscan/ports //用TCP的三次握手,以速率10000扫描1-65535端口,扫描结果以全格式…...
【2.3】Java微服务:sentinel服务哨兵
✅作者简介:大家好,我是 Meteors., 向往着更加简洁高效的代码写法与编程方式,持续分享Java技术内容。 🍎个人主页:Meteors.的博客 💞当前专栏:Java微服务 ✨特色专栏: 知识分享 &…...

【C++】开源:abseil-cpp基础组件库配置使用
😏★,:.☆( ̄▽ ̄)/$:.★ 😏 这篇文章主要介绍abseil-cpp基础组件库配置使用。 无专精则不能成,无涉猎则不能通。——梁启超 欢迎来到我的博客,一起学习,共同进步。 喜欢的朋友可以关注一下&#…...
【GPT-3 】创建能写博客的AI工具
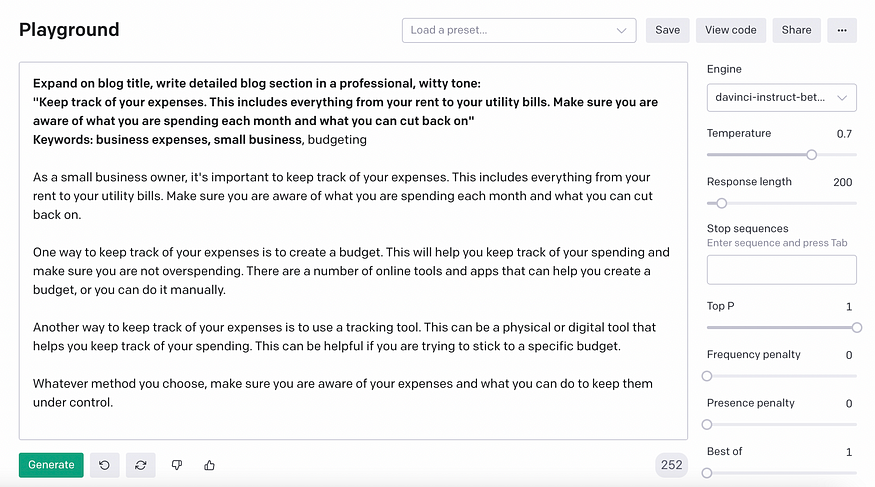
一、说明 如何使用OpenAI API,GPT-3和Python创建AI博客写作工具。 在本教程中,我们将从 OpenAI API 中断的地方继续,并创建我们自己的 AI 版权工具,我们可以使用它使用 GPT-3 人工智能 (AI) API 创建独特的…...
[保研/考研机试] KY35 最简真分数 北京大学复试上机题 C++实现
题目链接: 最简真分数https://www.nowcoder.com/share/jump/437195121691719749588 描述 给出n个正整数,任取两个数分别作为分子和分母组成最简真分数,编程求共有几个这样的组合。 输入描述: 每组包含n(n<600&…...

算法备案后,企业需要做什么?合规与执行挑战
随着技术的迅猛发展,算法已经成为多数企业核心竞争力的一部分。但在技术进步的同时,我们也面临了算法透明度、公平性以及安全性的问题。因此,许多国家已经开始实施算法备案制度,以确保算法的应用满足一定的标准和规范。但在完成算…...

云原生应用程序的自动化管理和编排
云原生应用程序是一种为云环境设计的应用程序,它采用了如微服务、容器、可伸缩性和自动化等特性,以最大限度地提高效率和响应速度。本文将深入探讨云原生应用如何实现自动化管理和编排。 容器化 容器技术,如Docker,是云原生应用程…...
Spring项目整合过滤链模式~实战应用
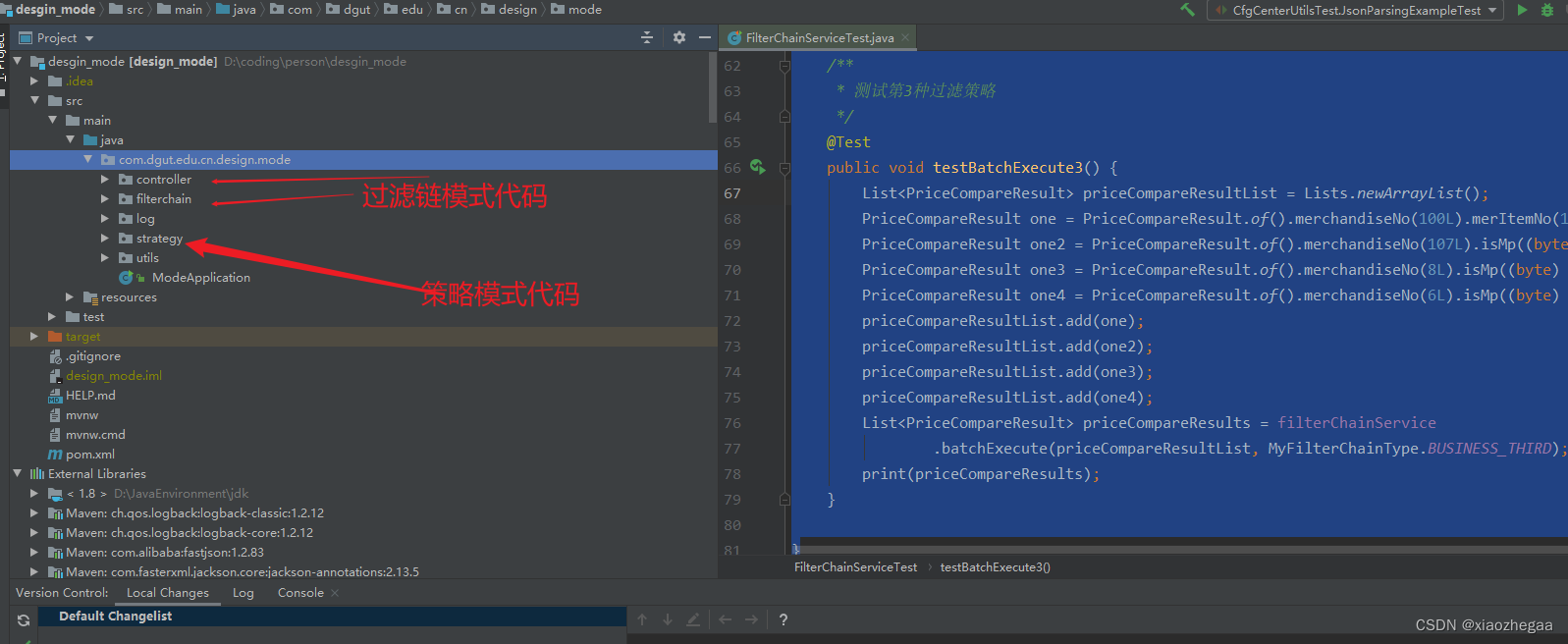
代码下载 设计模式代码全部在gitee上,下载链接: https://gitee.com/xiaozheng2019/desgin_mode.git 日常写代码遇到的囧 1.新建一个类,不知道该放哪个包下 2.方法名称叫A,干得却是A+B+C几件事情,随时隐藏着惊喜 3.想复用一个方法,但是里面嵌套了多余的逻辑,只能自己拆出来…...
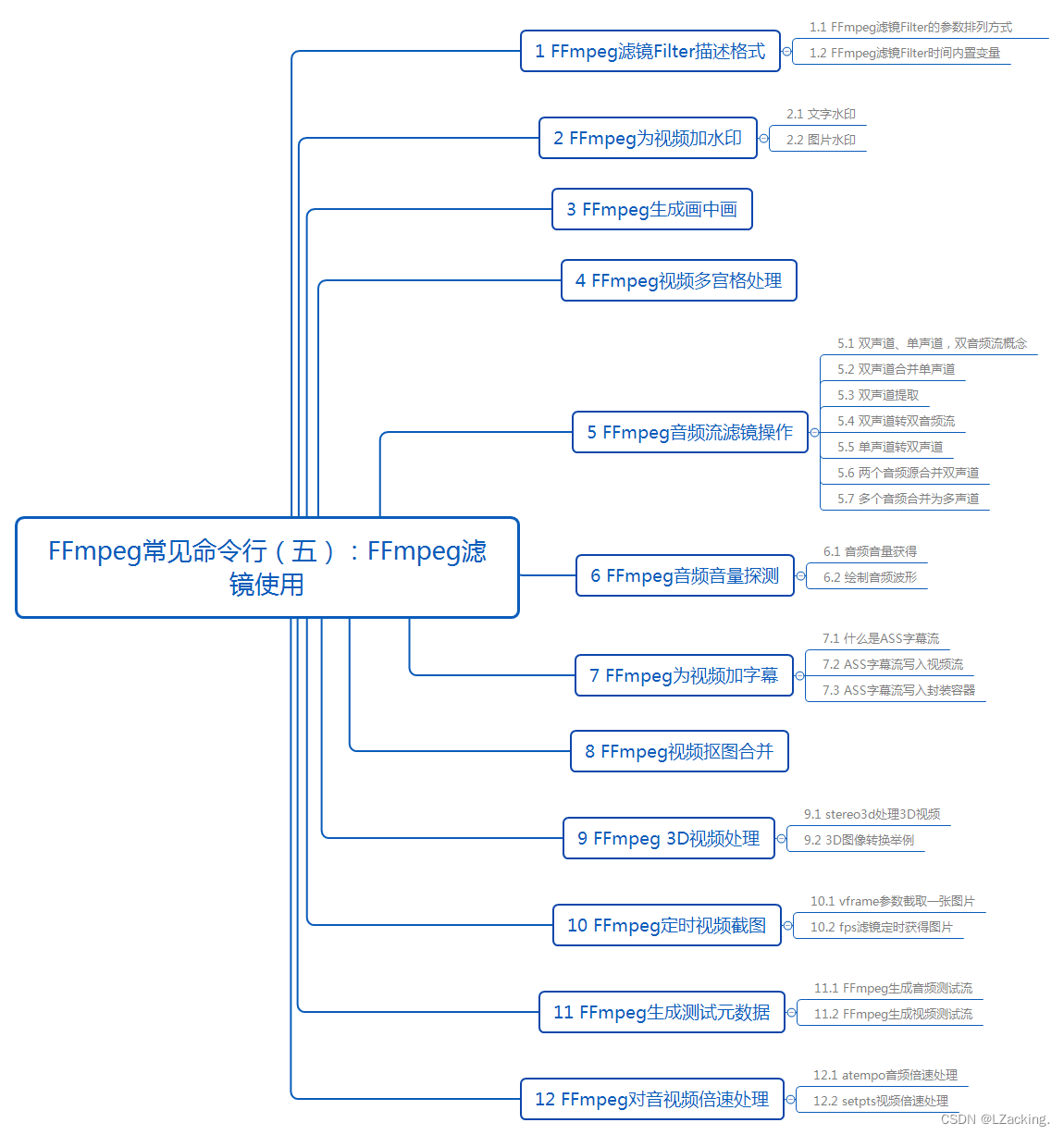
FFmpeg常见命令行(五):FFmpeg滤镜使用
前言 在Android音视频开发中,网上知识点过于零碎,自学起来难度非常大,不过音视频大牛Jhuster提出了《Android 音视频从入门到提高 - 任务列表》,结合我自己的工作学习经历,我准备写一个音视频系列blog。本文是音视频系…...
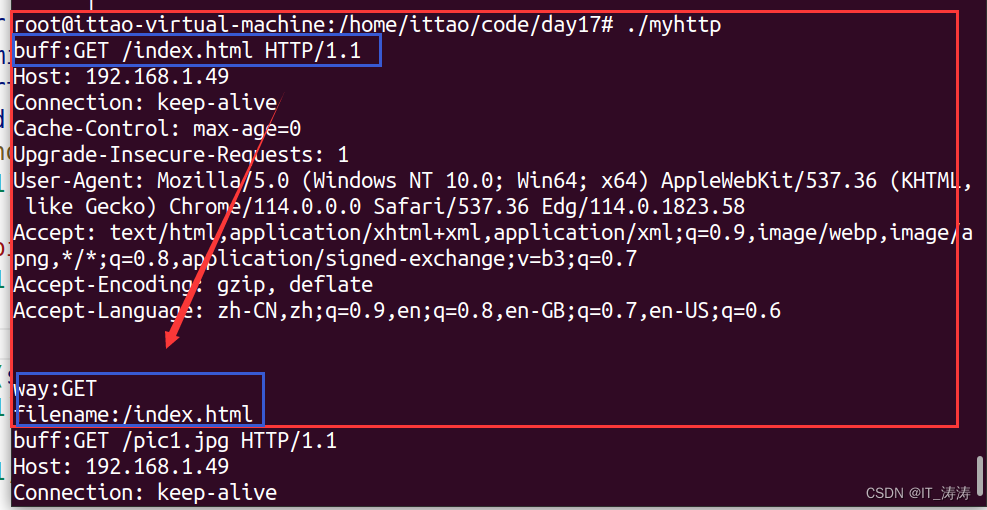
网络编程 tcp udp http编程流程 网络基础知识
讲解 网络基础知识网络编程tcp编程流程图示理解bind和accept函数理解监视套接字和链接套接字理解linux和window下的编程实现tcp特点 udp编程流程图示理解udp特点 http编程流程图示理解编程实现-网站服务器 网络基础知识 OSI分层:应用层 表示层 会话层 传输层 网络层…...
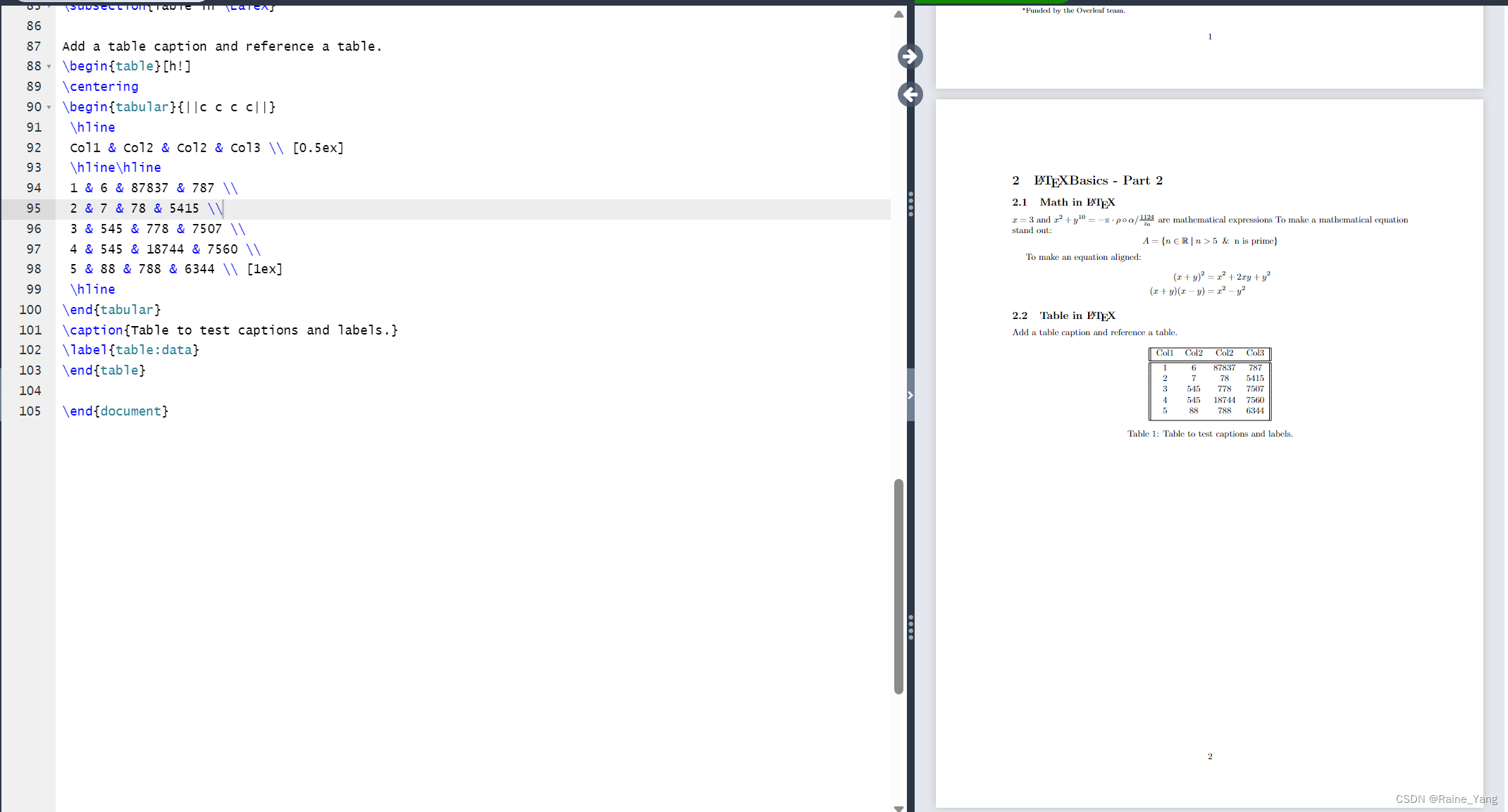
LaTeX基础学习笔记
LaTeX是一个文本编辑器。其类似于markdown,使用特殊标记和代码来修改文本格式,创建特殊字符等。可以使用overleaf在线LaTex编辑器编写LaTeX并转换为pdf文件(https://www.overleaf.com/) 同时推荐一个网站http://detexify.kirelab…...

zookeeper和kafka
目录 一、zookeeper理论 1.1、zookeeper定义 1.2、zookeeper工作机制 1.3、zookeeper特点 1.4、zookeeper的数据结构 1.5、zookeeper应用场景 1.6、zookeeper的选举机制 二、部署Zookeeper 集群 2.1、环境准备 2.2、安装 Zookeeper 2.3、修改配置文件 2.4、配置…...

服务器无法加载海康sdk依赖的问题
首先遇到的jna.jar和examples.jar无法加载的问题,尝试了很多方法无效,以下方法实测有效 其次是动态链接库无法加载的问题,而且是播放库,我的方法比较简单,netsdk加载出来就行了,播放库用不到,删…...

Opencv中的addweighted函数
一.addweighted函数作用 addweighted()是OpenCV库中用于图像处理的函数,主要功能是将两个输入图像(尺寸和类型相同)按照指定的权重进行加权叠加(图像融合),并添加一个标量值&#x…...

五年级数学知识边界总结思考-下册
目录 一、背景二、过程1.观察物体小学五年级下册“观察物体”知识点详解:由来、作用与意义**一、知识点核心内容****二、知识点的由来:从生活实践到数学抽象****三、知识的作用:解决实际问题的工具****四、学习的意义:培养核心素养…...

【决胜公务员考试】求职OMG——见面课测验1
2025最新版!!!6.8截至答题,大家注意呀! 博主码字不易点个关注吧,祝期末顺利~~ 1.单选题(2分) 下列说法错误的是:( B ) A.选调生属于公务员系统 B.公务员属于事业编 C.选调生有基层锻炼的要求 D…...

【Java_EE】Spring MVC
目录 Spring Web MVC 编辑注解 RestController RequestMapping RequestParam RequestParam RequestBody PathVariable RequestPart 参数传递 注意事项 编辑参数重命名 RequestParam 编辑编辑传递集合 RequestParam 传递JSON数据 编辑RequestBody …...

【论文阅读28】-CNN-BiLSTM-Attention-(2024)
本文把滑坡位移序列拆开、筛优质因子,再用 CNN-BiLSTM-Attention 来动态预测每个子序列,最后重构出总位移,预测效果超越传统模型。 文章目录 1 引言2 方法2.1 位移时间序列加性模型2.2 变分模态分解 (VMD) 具体步骤2.3.1 样本熵(S…...

MFC 抛体运动模拟:常见问题解决与界面美化
在 MFC 中开发抛体运动模拟程序时,我们常遇到 轨迹残留、无效刷新、视觉单调、物理逻辑瑕疵 等问题。本文将针对这些痛点,详细解析原因并提供解决方案,同时兼顾界面美化,让模拟效果更专业、更高效。 问题一:历史轨迹与小球残影残留 现象 小球运动后,历史位置的 “残影”…...

RSS 2025|从说明书学习复杂机器人操作任务:NUS邵林团队提出全新机器人装配技能学习框架Manual2Skill
视觉语言模型(Vision-Language Models, VLMs),为真实环境中的机器人操作任务提供了极具潜力的解决方案。 尽管 VLMs 取得了显著进展,机器人仍难以胜任复杂的长时程任务(如家具装配),主要受限于人…...

十九、【用户管理与权限 - 篇一】后端基础:用户列表与角色模型的初步构建
【用户管理与权限 - 篇一】后端基础:用户列表与角色模型的初步构建 前言准备工作第一部分:回顾 Django 内置的 `User` 模型第二部分:设计并创建 `Role` 和 `UserProfile` 模型第三部分:创建 Serializers第四部分:创建 ViewSets第五部分:注册 API 路由第六部分:后端初步测…...

Java求职者面试指南:Spring、Spring Boot、Spring MVC与MyBatis技术解析
Java求职者面试指南:Spring、Spring Boot、Spring MVC与MyBatis技术解析 一、第一轮基础概念问题 1. Spring框架的核心容器是什么?它的作用是什么? Spring框架的核心容器是IoC(控制反转)容器。它的主要作用是管理对…...

comfyui 工作流中 图生视频 如何增加视频的长度到5秒
comfyUI 工作流怎么可以生成更长的视频。除了硬件显存要求之外还有别的方法吗? 在ComfyUI中实现图生视频并延长到5秒,需要结合多个扩展和技巧。以下是完整解决方案: 核心工作流配置(24fps下5秒120帧) #mermaid-svg-yP…...
