面试热题(路径总和II)
给你二叉树的根节点
root和一个整数目标和targetSum,找出所有 从根节点到叶子节点 路径总和等于给定目标和的路径。叶子节点 是指没有子节点的节点。
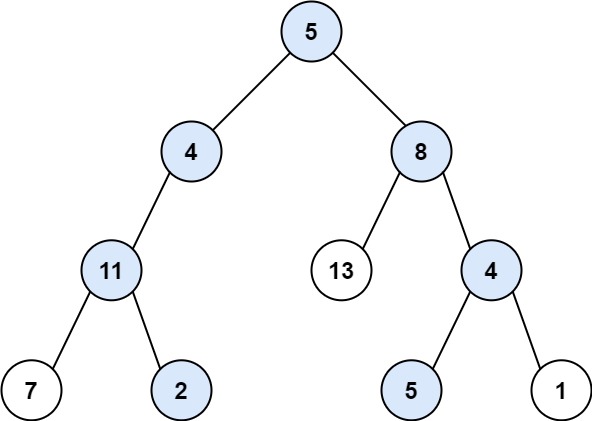
在这里给大家提供两种方法进行思考,第一种方法是递归,第二种方式使用回溯的方式进行爆搜
递归:树具有天然的递归结构,将一个大的问题转换成多个相同的子问题而进行解决,就相当于你会0-1的算式,你自然而然可以推导出0-n的算式(递归终止条件+递归操作)
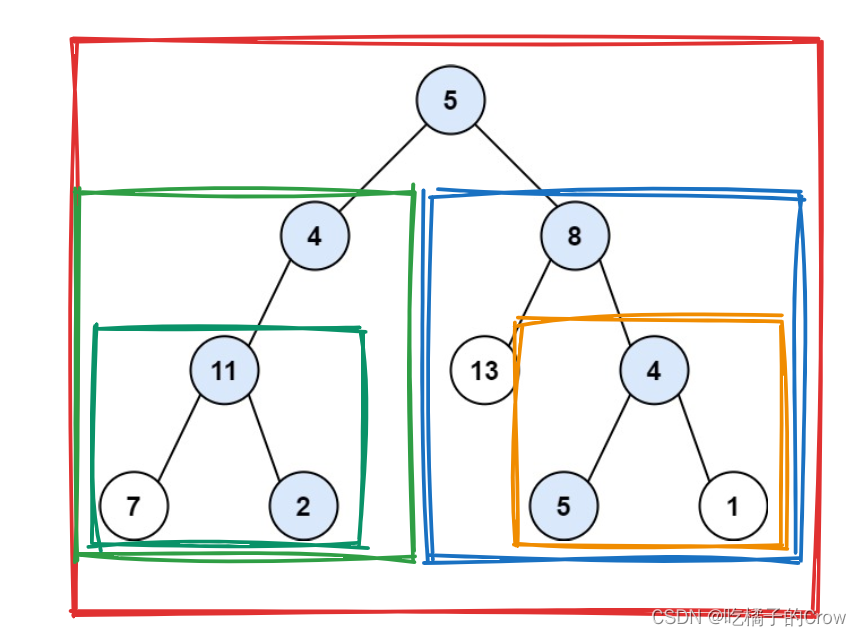
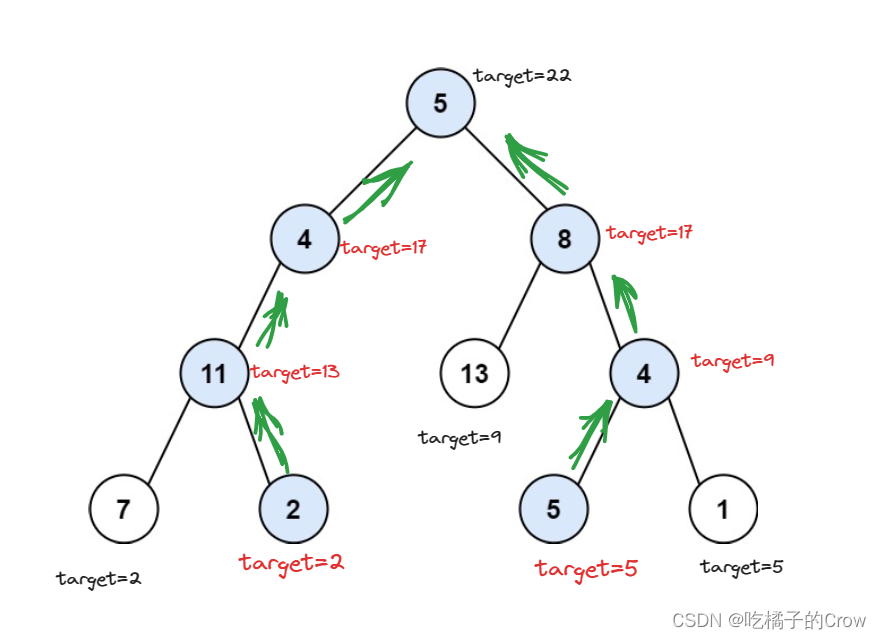
我觉的这个图可以很形象的说明一些问题,通过改变每个结点的差值,最后进行叶子结点与传入的target进行比较,如果相等,就说明树中肯定有满足情况的路径
解题步骤:
- 方法中返回什么,我们就创建什么
public List<List<Integer>> pathSum(TreeNode root, int targetSum) {List<List<Integer>> resList=new LinkedList<>();...}- 递归结束的条件(分为第一次入参和叶子结点的入参,两者的操作不一样)
//如果传进行的叶子结点为空,直接返回一个空链表if(root==null){return resList;}//如果是叶子结点且叶子结点的值等于target,则该叶子结点是满足情况下的一条路径上的值if(root.left==null&&root.right==null){if(root.val==targetSum){List<Integer> list=new LinkedList<>();list.add(root.val);//将该路径加入总结果集中resList.add(list);}return resList;}- 每次递归的时候将target-root.val作为参数传下去
int diff=targetSum-root.val;- 如果左树不为空,递归左树,如果右树不为空,递归右树
if(root.left!=null){List<List<Integer>> curList=pathSum(root.left,diff);for(int i=0;i<curList.size();i++){List<Integer> list1=curList.get(i);//将该节点加入路径中list1.add(0,root.val);//加入到结果集中resList.add(list1);}}if(root.right!=null){List<List<Integer>> curList=pathSum(root.right,diff);for(int i=0;i<curList.size();i++){List<Integer> list1=curList.get(i);list1.add(0,root.val);resList.add(list1);}}- 最后每次递归结束后返回结果集,供归的时候进行使用
return resList;方法二:回溯
回溯的方法相当于暴力搜索一样,但是对于面试而言,我更加推荐回溯(比较容易记忆)
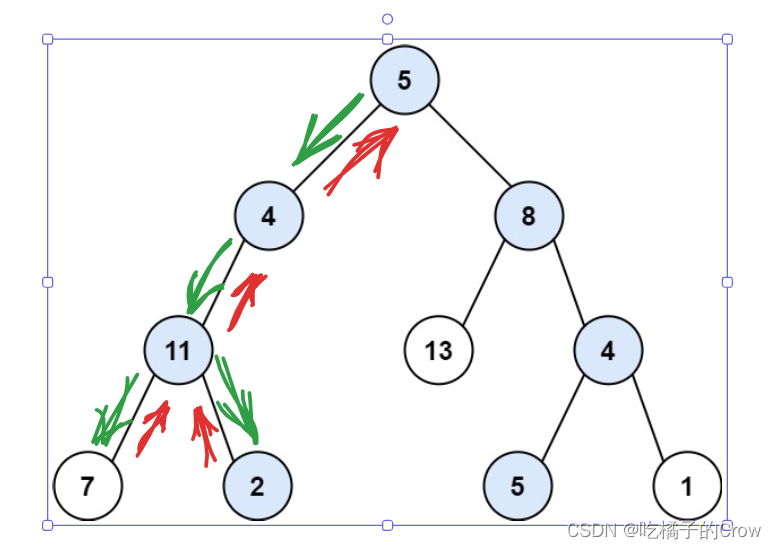
//大体思想其实和递归差不多,就是回溯这种题有个特定的模板,有的时候,即使你不会做,那你也有可能把题做出来List<List<Integer>> resList=new LinkedList<>();List<Integer> path=new LinkedList<>();public List<List<Integer>> pathSum(TreeNode root, int targetSum) {if(root==null){return resList;}backtracing(root,targetSum);return resList;}public void backtracing(TreeNode root,int targetSum){if(root==null){return;}path.add(root.val);if(targetSum==root.val&&root.left==null&&root.right==null){resList.add(new ArrayList<>(path));}int diff=targetSum-root.val;if(root.left!=null){pathSum(root.left,diff);//回溯path.remove(path.size()-1);}if(root.right!=null){pathSum(root.right,diff);path.remove(path.size()-1);}}相关文章:

面试热题(路径总和II)
给你二叉树的根节点 root 和一个整数目标和 targetSum ,找出所有 从根节点到叶子节点 路径总和等于给定目标和的路径。 叶子节点 是指没有子节点的节点。 在这里给大家提供两种方法进行思考,第一种方法是递归,第二种方式使用回溯的方式进行爆…...

测试 tensorflow 1.x 的一个demo 01
tensorflow 1.0的示例代码 demo_01.py import tensorflow as tf import os os.environ[TF_CPP_MIN_LOG_LEVEL]2def tf114_demo():a 3b 4c a bprint("a b in py ",c)a_t tf.constant(3)b_t tf.constant(4)c_t a_t b_tprint("TensorFlow add a_t b_t &…...

达蒙DM数据库使用经验
DM表/字段注释 注:dm数据库无法在建表的同时为字段名添加注释 //为表添加注释 comment on table 库名.表名 is 表注释; //为表字段添加注释 comment on column 库名.表名.列名 is 列注释;DM查询错误:无效的表或视图 1,确认表一定存在 2&am…...
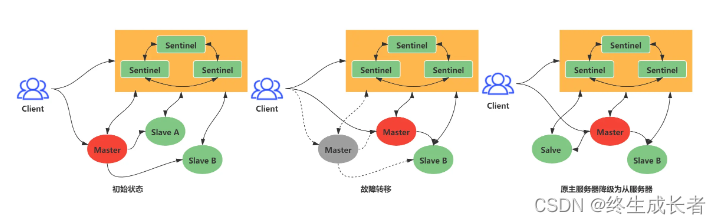
Redis—集群
目录标题 主从复制第一次同步命令传播分担主服务器压力增量复制总结面试题什么是Redis主从复制Redis主从复制的原理Redis主从复制的优点Redis主从复制的缺点Redis主从复制的配置步骤Redis主从复制的同步策略主从节点是长还是短连接判断某个节点是否正常工作主从复制架构中&…...
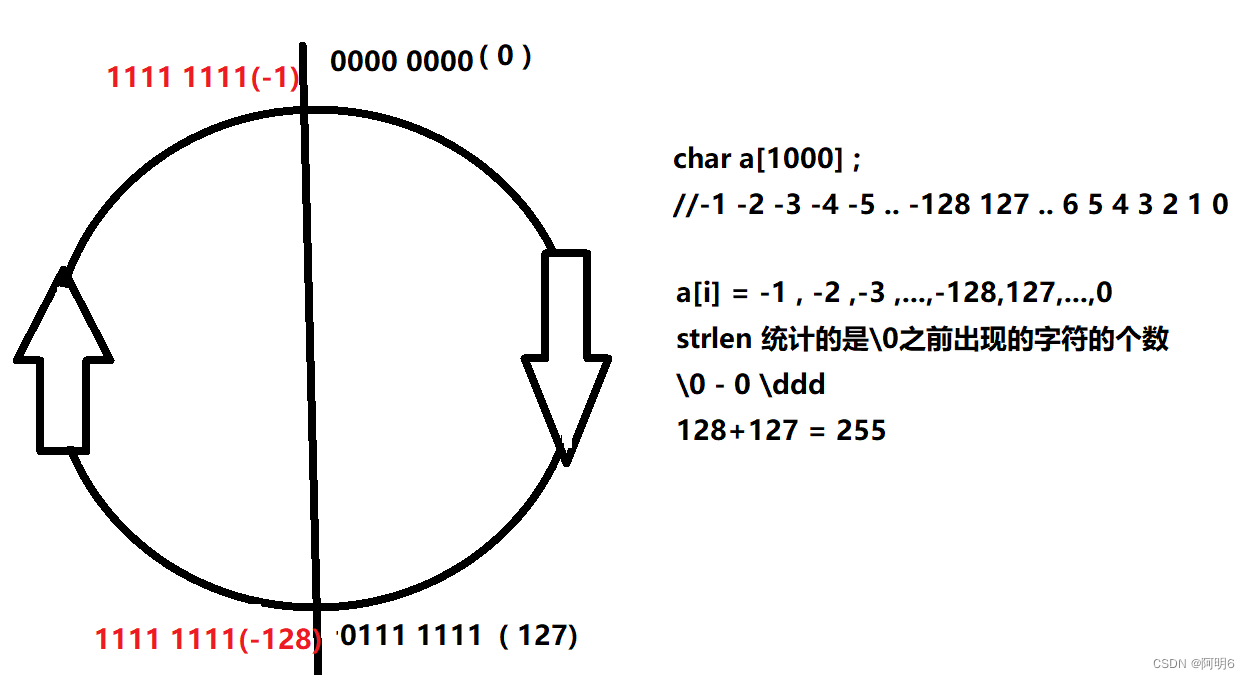
【C语言】数据在内存中的存储详解
文章目录 一、什么是数据类型二、类型的基本归类三、 整型在内存中的存储1.原码、反码、补码2.大小端(1)什么是大小端(2)为什么会有大小端 四、浮点型在内存中的存储1. 浮点数存储规则 五、练习1.2.3.4.5.6.7. 一、什么是数据类型 我们可以把数据类型想象为一个矩形盒子&#x…...

PIC单片机配置字的设置
PIC单片机配置字的设置 PIC系列单片机,其芯片内部大都设置有一个特殊的程序存储单元,地址根据不同的单片机而定,此存储单元用来由单片机用户自由配置或定义单片机内部的一些功能电路单元的性能选项,所以被称之为系统配置字。目前PIC单片机系统配置字的方法有两种,一种是利…...
JavaWeb-Servlet服务连接器(一)
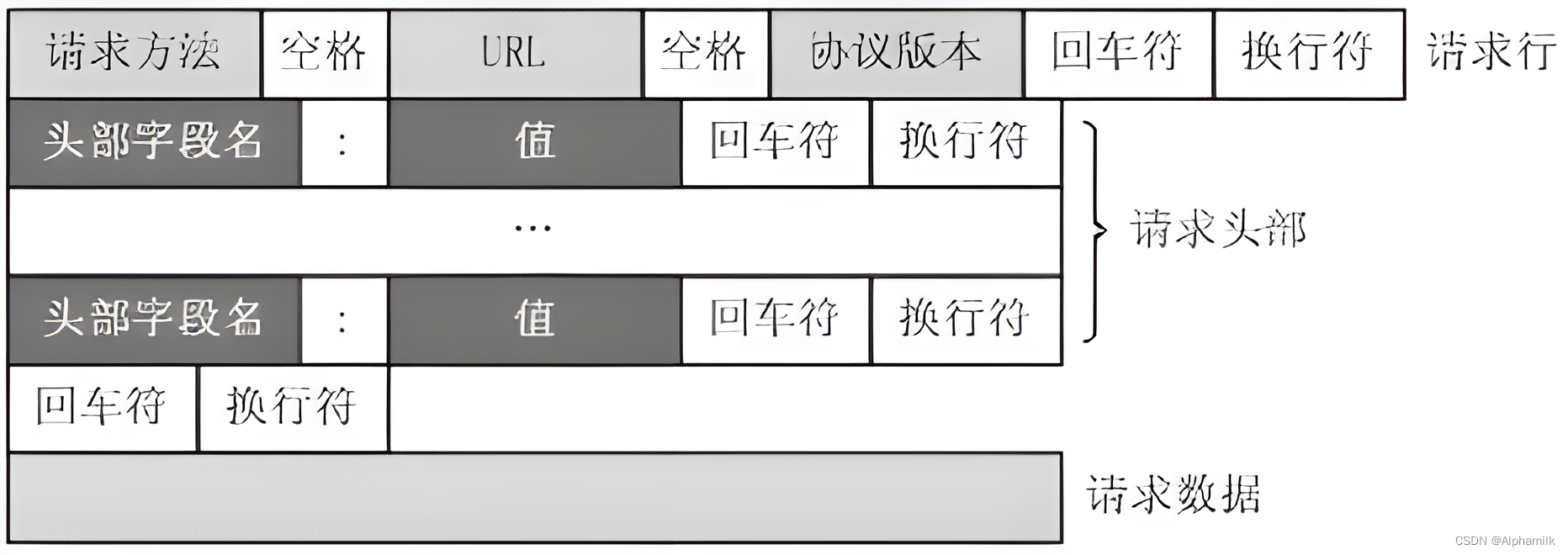
目录 1.Servlet生命周期 2.Servlet的配置 3.Servlet的常用方法 4.Servlet体系结构 5.HTTP请求报文 6.HTTP响应报文 1.Servlet生命周期 Servlet(Server Applet)是Java Servlet的简称。其主要的功能是交互式地浏览和修改数据,生成一些动态…...

新华三超融合态势感知标准版
产品概述: H3C SecCenter CSAP-XS 超融合态势感知一体机产品集合了态势感知和安全流量分析探针设备能无需复杂配置;态势感知平台具备强大的安全分析和可视化呈现功能;同时具备远程专家会诊功能,通过云端协同实现外部安全服务资源的…...
13.2-Mcal Port配置)
AutoSAR系列讲解(深入篇)13.2-Mcal Port配置
目录 一、配置界面 二、通用配置 1、ConfigVariant 2、PortSafety 3、PortGeneral 三、Port配置集合...
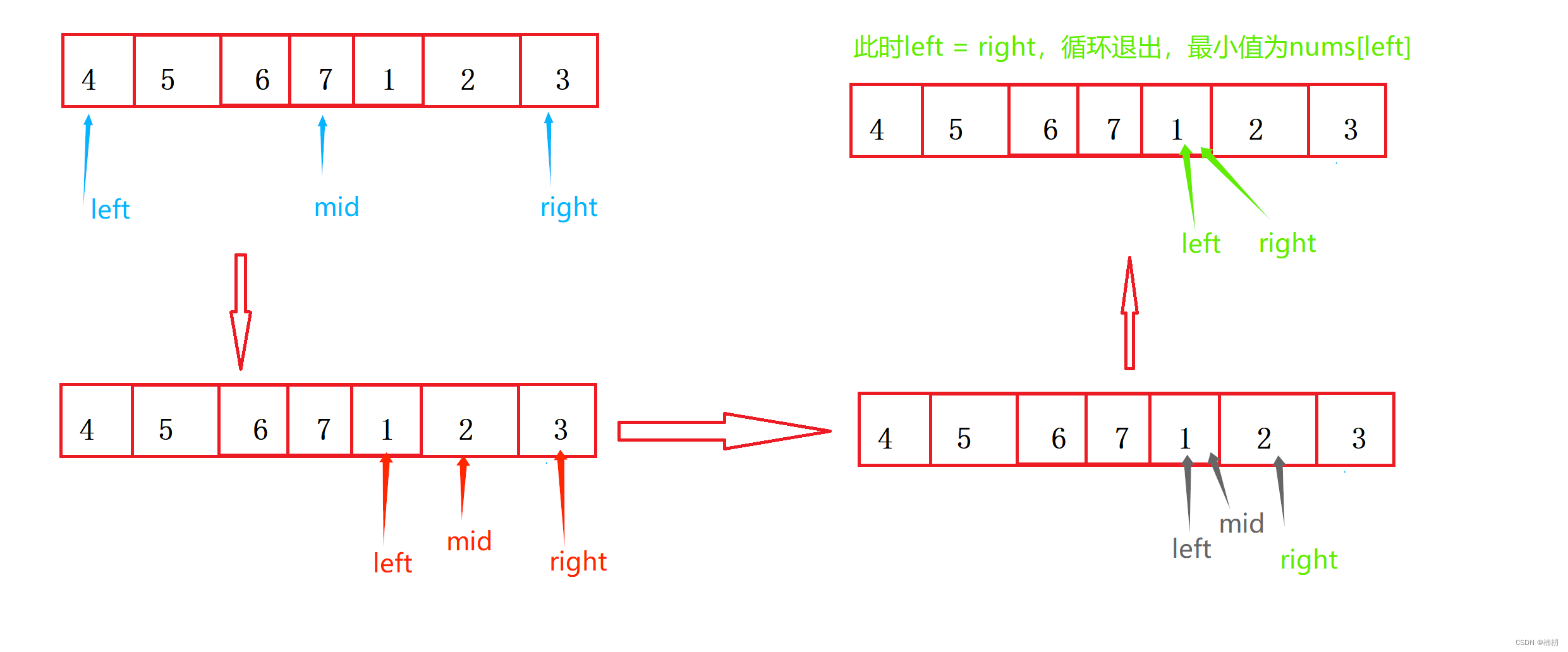
Java旋转数组中的最小数字(图文详解版)
目录 1.题目描述 2.题解 分析 具体实现 方法一(遍历): 方法二(排序): 方法三(二分查找): 1.题目描述 有一个长度为 n 的非降序数组,比如[1,2,3,4,5]&a…...

Android 13 Hotseat定制化修改——005 hotseat图标禁止形成文件夹
目录 一.背景 二.方案 一.背景 由于需求是需要自定义修改Hotseat,所以此篇文章是记录如何自定义修改hotseat的,应该可以覆盖大部分场景,修改点有修改hotseat布局方向,hotseat图标数量,hotseat图标大小,hotseat布局位置,hotseat图标禁止形成文件夹,hotseat图标禁止移动…...
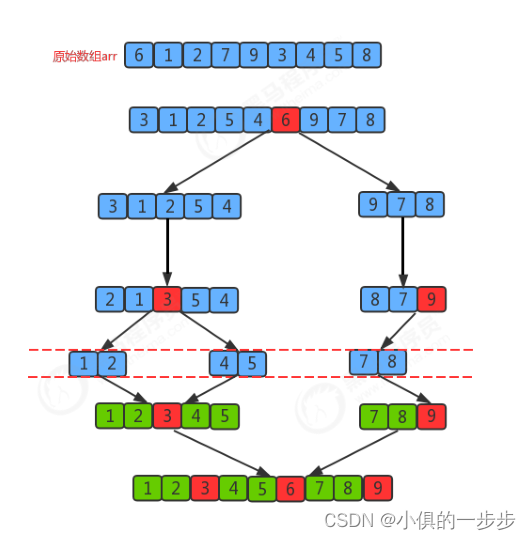
插入、希尔、归并、快速排序(java实现)
目录 插入排序 希尔排序 归并排序 快速排序 插入排序 排序原理: 1.把所有元素分为两组,第一组是有序已经排好的,第二组是乱序未排序。 2.将未排序一组的第一个元素作为插入元素,倒序与有序组比较。 3.在有序组中找到比插入…...
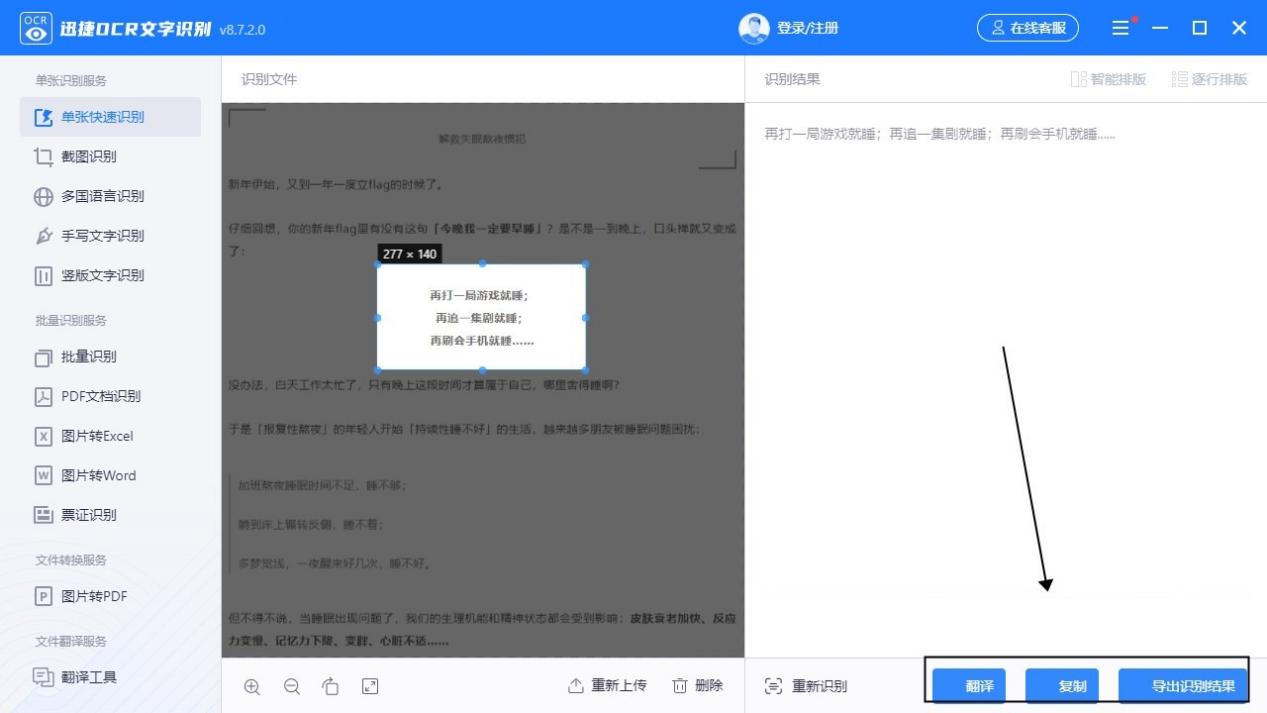
怎么把图片表格转换成word表格?几个步骤达成
在处理文档时,图片表格的转换是一个常见的需求。而手动输入表格是非常耗时的,因此,使用文本识别软件来自动转换图片表格可以大大提高工作效率。在本文中,我们将介绍如何使用OCR文字识别技术来将图片表格转换为Word表格。 OCR文字识…...
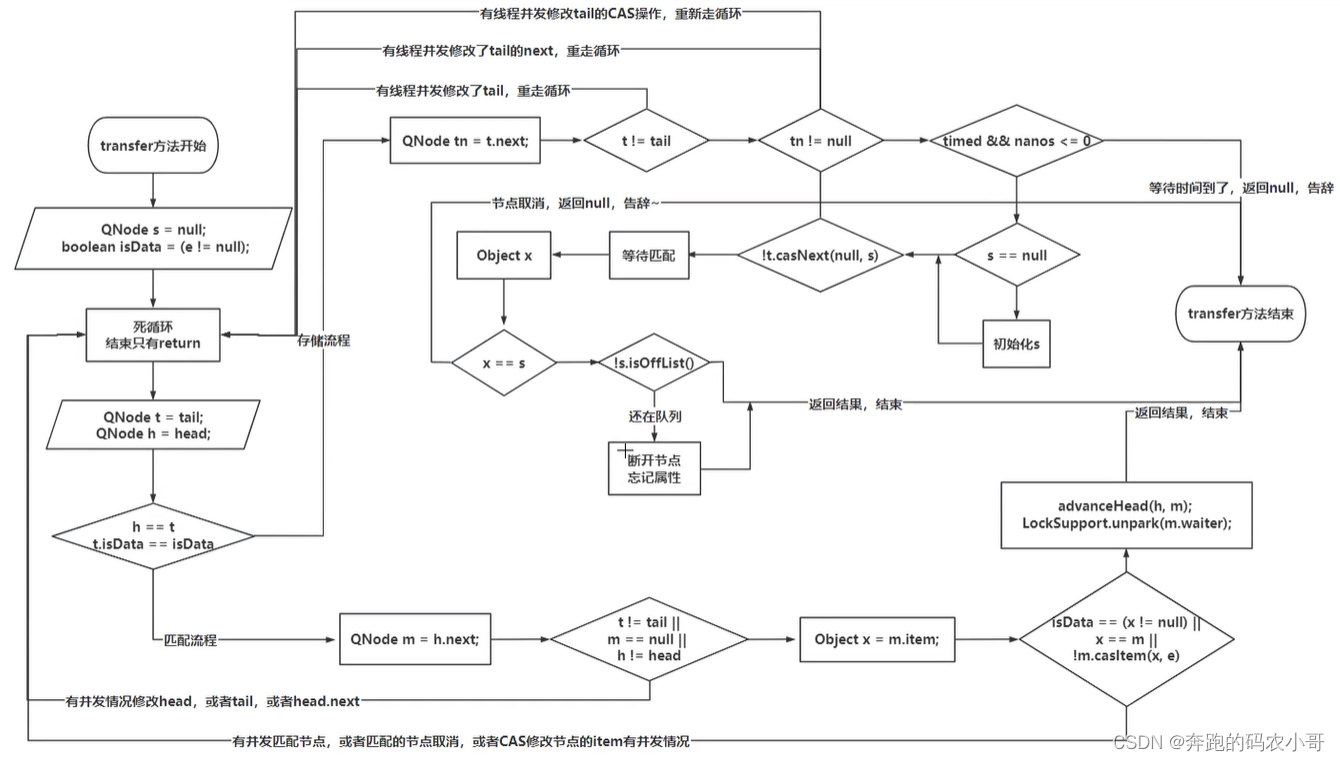
多线程与高并发--------阻塞队列
四、阻塞队列 一、基础概念 1.1 生产者消费者概念 生产者消费者是设计模式的一种。让生产者和消费者基于一个容器来解决强耦合问题。 生产者 消费者彼此之间不会直接通讯的,而是通过一个容器(队列)进行通讯。 所以生产者生产完数据后扔到…...

前端-NVM,Node.js版本管理
NVM(Node Version Manager)是一个用于管理Node.js版本的工具,主要用于前端开发中。它允许开发者同时安装和切换不同版本的Node.js,以满足不同项目对Node.js版本的需求。 使用NVM可以带来以下几个好处: 多版本管理&…...

React - useEffect函数的理解和使用
文章目录 一,useEffect描述二,它的执行时机三,useEffect分情况使用1,不写第二个参数 说明监测所有state,其中一个变化就会触发此函数2,第二个参数如果是[]空数组,说明谁也不监测3,第…...

python模块 — 加解密模块rsa,cryptography
一、密码学 1、密码学介绍 密码学(Cryptography)是研究信息的保密性、完整性和验证性的科学和实践。它涉及到加密算法、解密算法、密钥管理、数字签名、身份验证等内容。 密码学中的主要概念包括: 1. 加密算法:加密算法用于将…...
)
【C++】速识模板(template<class T>)
一、引言 在我们学习C时,常会用到函数重载。而函数重载,通常会需要我们编写较为重复的代码,这就显得臃肿,且效率低下。 重载的函数仅仅只是类型不同,代码的复用率比较低,只要有新类型出现时,就…...

腾讯云10万日活服务器配置怎么选?费用多少?
日活10万的小程序或APP使用腾讯云服务器配置怎么选?腾讯云10万人服务器配置多少钱一年?可以选择腾讯云4核8G12M轻量应用服务器或8核16G18M服务器,云服务器CVM的话可以选择标准型S5实例,腾讯云服务器网来详细说下腾讯云日活10万服务…...
)
vue 使用vue-video-player加载视频(铺满容器)
vue 使用vue-video-player加载视频(铺满容器) 安装 npm install vue-video-player --savemain.js 引入 import VideoPlayer from "vue-video-player" import "video.js/dist/video-js.css" import "vue-video-player/src/custom-theme.css" i…...

<6>-MySQL表的增删查改
目录 一,create(创建表) 二,retrieve(查询表) 1,select列 2,where条件 三,update(更新表) 四,delete(删除表…...

DockerHub与私有镜像仓库在容器化中的应用与管理
哈喽,大家好,我是左手python! Docker Hub的应用与管理 Docker Hub的基本概念与使用方法 Docker Hub是Docker官方提供的一个公共镜像仓库,用户可以在其中找到各种操作系统、软件和应用的镜像。开发者可以通过Docker Hub轻松获取所…...
` 方法)
深入浅出:JavaScript 中的 `window.crypto.getRandomValues()` 方法
深入浅出:JavaScript 中的 window.crypto.getRandomValues() 方法 在现代 Web 开发中,随机数的生成看似简单,却隐藏着许多玄机。无论是生成密码、加密密钥,还是创建安全令牌,随机数的质量直接关系到系统的安全性。Jav…...

Java面试专项一-准备篇
一、企业简历筛选规则 一般企业的简历筛选流程:首先由HR先筛选一部分简历后,在将简历给到对应的项目负责人后再进行下一步的操作。 HR如何筛选简历 例如:Boss直聘(招聘方平台) 直接按照条件进行筛选 例如:…...

算法笔记2
1.字符串拼接最好用StringBuilder,不用String 2.创建List<>类型的数组并创建内存 List arr[] new ArrayList[26]; Arrays.setAll(arr, i -> new ArrayList<>()); 3.去掉首尾空格...

中医有效性探讨
文章目录 西医是如何发展到以生物化学为药理基础的现代医学?传统医学奠基期(远古 - 17 世纪)近代医学转型期(17 世纪 - 19 世纪末)现代医学成熟期(20世纪至今) 中医的源远流长和一脉相承远古至…...

【电力电子】基于STM32F103C8T6单片机双极性SPWM逆变(硬件篇)
本项目是基于 STM32F103C8T6 微控制器的 SPWM(正弦脉宽调制)电源模块,能够生成可调频率和幅值的正弦波交流电源输出。该项目适用于逆变器、UPS电源、变频器等应用场景。 供电电源 输入电压采集 上图为本设计的电源电路,图中 D1 为二极管, 其目的是防止正负极电源反接, …...

MySQL 部分重点知识篇
一、数据库对象 1. 主键 定义 :主键是用于唯一标识表中每一行记录的字段或字段组合。它具有唯一性和非空性特点。 作用 :确保数据的完整性,便于数据的查询和管理。 示例 :在学生信息表中,学号可以作为主键ÿ…...

Qt 事件处理中 return 的深入解析
Qt 事件处理中 return 的深入解析 在 Qt 事件处理中,return 语句的使用是另一个关键概念,它与 event->accept()/event->ignore() 密切相关但作用不同。让我们详细分析一下它们之间的关系和工作原理。 核心区别:不同层级的事件处理 方…...

CVPR2025重磅突破:AnomalyAny框架实现单样本生成逼真异常数据,破解视觉检测瓶颈!
本文介绍了一种名为AnomalyAny的创新框架,该方法利用Stable Diffusion的强大生成能力,仅需单个正常样本和文本描述,即可生成逼真且多样化的异常样本,有效解决了视觉异常检测中异常样本稀缺的难题,为工业质检、医疗影像…...
