Redis进阶:布隆过滤器(Bloom Filter)及误判率数学推导
1 缘起
有一次偶然间听到有同事在说某个项目中使用了布隆过滤器,
哎呦,我去,我竟然不知道啥是布隆过滤器,
这我哪能忍?其实,也可以忍,但是,可能有的面试官不能忍!!!
于是,查询了布隆过滤器的相关知识,
特分享如下,帮助读者轻松应对知识交流与考核。
Wiki文档:https://en.wikipedia.org/wiki/Bloom_filter#Probability_of_false_positives
2 布隆过滤器
布隆过滤器是一种空间有效(Space efficient)的概率型数据结构。
是Burton Howard于1970年提出的,用于测试元素是否存在于某个集合。
这里有假阳性(误判,可能存在)和假阴性(正确判断,一定不存在)两个概念,
假阳性标识元素可能存在于集合中;
假阴性标识元素一定不存在于集合中;
需要注意的是,元素添加到布隆过滤器后,不可删除(可以通过计数布隆过滤器变量解决),
添加的元素越多,误判率越高。
因为使用“常规”无错hash技术处理大量源数据需要消耗大量内存,所以Bloom提出了一种处理技术。
他举了一个50万单词断字算法的例子,90%的数据遵循简单的断字规则,10%的需要昂贵的磁盘访问才能检索特定的断字模式。
有了足够的核心内存,可以使用无错hash消除不必要的磁盘访问,有限的核心中,虽然Bloom技术使用了较小的hash区域,
但依旧消除了大多数不必要的访问。比如,只需理想无错hash 15%的hash区域即可消除85%的磁盘访问。
对于1%的假阳性概率,每个元素至少小于10bit,与集合中元素的大小或数量无关。
空的布隆过滤器是一个m位的位数组,全部置为0.
同时,需要定义k个不同的hash函数,每个hash函数将集合元素映射或hash到m个数组的位置,从而生成统一的随机分布。
一般,k是一个小常数,这取决于期望的错误率ε,而m与k和要添加的元素数量成比例。
设计k个不同的hash函数对于大k而言是不允许的。
对于较大范围输出的优秀hash函数而言,hash不同的字段几乎是没有相关性的,
因此,这种类型的hash可以将输出分为多个位字段来生成多个不同的hash函数(字段不同,hash结果大概率不同,因此等价于不同的hash函数)。
或者,将k个具有不同初始值(如0,1,…,k-1)元素传给hash函数;或者将这些值附加到键上。
对于较大的m或k,可以扩大hash函数的独立性,假阳性(误判)的概率可以忽略不计。
Dillinger & Manolios展示了使用增强hash和三次hash来推导k个索引的有效性,双hash的变体是有效的简单随机数生成器(使用两个或三个hash值作为种子)。
布隆过滤器中的元素是无法移除(删除)的,因为无法确定这个位置的数据是否真的应该删除,
为什么会这样?因为,删除元素时需要将元素映射在布隆过滤器数组值置为0,
所以,就有可能将已存在元素的数组值给误替了,导致已存在元素反而被误删了
(核心问题:无法确定要删除的元素是否一定在布隆过滤器中,元素a和元素b可能有某个hash值重合,所以,会出现这个问题,这也就阻止了想用计数方式存储数据的方案了,相同位置+1,但是布隆过滤器数组中的值只有0和1)。
可以通过第二层布隆过滤器模拟删除元素的操作,
第二个布隆过滤器存储删除的元素,不过,这种方式无法重新添加已元素到布隆过滤器中,
因为第二个布隆过滤器已经存在这个元素了,必须从第二个布隆过滤器中删除才行。
一般,所有键都是可用的,但是枚举(遍历)是非常昂贵的(如需要更多的磁盘空间)。
当假阳性(误判)比例过高时,可以重建布隆过滤器,不过这是非常少见的。
2.1 空间和时间优势
虽然布隆过滤器有误报的风险,但是,相对于其他集合(如自平衡二叉树、Trie树、哈希表、简单数组或链表)而言,布隆过滤器有较大的空间优势。
其中大多数数据结构至少需要存储数据项本身,这样通常需要的存储空间会从几个bit(如小整数)到任意bit(如字符串),而trie则是一个例外,因为它们可以共用相同的前缀。
而布隆过滤器不需要存储数据项,因此需要为实际存储提供单独的解决方案。
链表结构需要为指针提供额外的存储空间。
相反,布隆过滤器1%的误差和最佳k次hash的每个元素只需9.6bit,不论元素有多大。
这种优势部分来自于布隆过滤器的紧凑性,继承了数组的特性,另一部分来源于概率模型,1%的假阳性(误判)可以通过为每个元素仅增加4.8bit而减少10倍。
如果潜在值的数量很小,并且其中许多值可以在集合中,那么布隆过滤器相关优势容易被确定性位阵列超越,
确定性位阵列只需每个潜在元素的1bit。如果hash表开始忽略冲突并只存储每个每个桶是否含有元素,那么,hash表将有空间和时间上的优势。这种情况下,实际上就是k=1的布隆过滤器。
布隆过滤器的特殊属性如向集合中添加或检查元素的时间是常量:O(k),与集合中的元素数量是无关的。
其他恒定空间的数据结构则没有这个特性,但是,稀疏hash表的平均访问时间在实际应用中可以比布隆过滤器少。
然而,在硬件实现中,布隆过滤器则非常优秀,因为他的k个查找是独立的,可以并行执行。
为理解布隆过滤器的空间效率,将一般的布隆过滤器与k=1的特殊布隆过滤器相比是非常有用的。
k=1时,为了保持较低的假阳性(误判率),应该配置小分位,这也意味着数组必须非常大,并且包含长串的0.
数组的内容量相对于尺寸是非常低的(内容可以很少,但是可以消耗更多数组位置)。
广义上布隆过滤器(k>1)允许配置更多的bit,同时保持较低的假阳性(误判率),如果k和m配置合适,会有一般的位置被正确利用,
并且这些bit都是随机分配的,从而最小化冗余,最大化信息内容。
2.2 解决什么问题?
判断一个元素是否存在于某个集合中,有一定的误判率。
本文对误判率进行数学推导,详见后文。
2.3 判断原则?
某个元素不在集合中,则该集合一定不存在这个元素;
某个元素在集合中,则该集合可能存在这个元素,存在判断误差;
2.4 如何插入数据?
这个要从布隆过滤器的构成说起,布隆过滤器是由一个很长的bit数组和一系列hash函数组成,数组中的每个元素都只占1bit空间,每个元素值只能是0或1。布隆过滤器有k个hash函数,当一个元素添加到布隆过滤器时,会用k个hash函数进行k次hash计算,得到k个hash值,根据得到的hash值,将数组对应标的值置为1,即hash的置为数组下标(索引)。
判断某个元素是否在布隆过滤器时,通用对该元素进行k次hash计算,根据得到的数组下表获取数组的值,当所有数组值为1时,判定元素可能存在于布隆过滤器。
2.5 为什么会有误判?
随着大量的数据添加到布隆过滤器,当一个不在布隆过滤器的元素进行hash计算后,根据得到的数组下标查询数据时,这些数据被其他元素在插入时置为1了,则会误判该元素存在于布隆过滤器。
hash冲突的原因。假设元素a和元素b具有相同的hash值,同时假定进行3次hash计算,hash值为1,2,3
将元素a插入了布隆过滤器,a[1]=a[2]=a[3]=1
元素b没有插入布隆过滤器,
当查询元素b时,经过hash计算,得到的数组下标为1,2,3,由于元素a将这些数据置为1,
则判断b元素存在于布隆过滤器,误判就出现了。
2.6 为什么不能删除元素
根据布隆过滤器的相关特性可知,
因为删除元素时无法确定这个位置的数据是否真的应该删除,
删除元素时需要将元素映射在布隆过滤器数组值置为0,
所以,就有可能将已存在元素的数组值给误替了,导致已存在元素反而被误删了
(核心问题:无法确定要删除的元素是否一定在布隆过滤器中,元素a和元素b可能有某个hash值重合,所以,会出现这个问题,这也就阻止了想用计数方式存储数据的方案了,相同位置+1,但是布隆过滤器数组中的值只有0和1)。
2.7 工作过程
下面来看一下Wiki:https://en.wikipedia.org/wiki/Bloom_filter#Probability_of_false_positives中介绍的布隆过滤器工作过程。
现构建长度为8的布隆过滤器(长度为8的数组)m=8,hash次数为3,k=3,
添加三个元素x、y和z,经过三次hash后,分别落在各自的数组位置,如下图所示,
由图可知,其他未插入元素的位置均为0,初始化时数组所有位置均置为0,当插入元素时,将hash后的位置置为1。
查询元素是否在布隆过滤器时,查询元素时,对元素进行k次hash,获取数组索引,查询对应的位值(0或1),
只有所有的位值为1,才判定元素可能存于布隆过滤器,即,只要查询元素通过hash后获取的数组值存在0,则一定不存在于布隆过滤器。
如查询元素w,进行k=3次hash后,获取的hash值对应的数组值含有0,所以,w不存在于布隆过滤器。

2.8 应用场景
(1)网页URL去重,避免爬取相同的URL;
(2)垃圾邮箱过滤;
(3)推荐系统:针对不希望重复推荐的场景,如文章推荐、广告推荐的非重复性推荐场景;
(4)解决缓存穿透:使用布隆过滤器,当不存在该数据时,直接返回,不会将大量请求涌入到持久层(如关系型数据库MySQL);
(5)秒杀系统:某些商品,一个ID只允许购买一次;
等等一系列需要判断元素是否存在的应用场景。
3 误判率数学推导过程
3.1 参数
m:布隆过滤器长度
n:已添加的元素数量
k:hash的次数
3.2 误判率
布隆过滤器某个位不置为1的概率:
1−1m1-{\frac {1}{m}}1−m1
哈希k次某个位置不置为1的概率:
(1−1m)k\left(1-{\frac {1}{m}}\right)^{k}(1−m1)k
根据极限:
limm→∞(1−1m)m=1e{\displaystyle \lim _{m\to \infty }\left(1-{\frac {1}{m}}\right)^{m}={\frac {1}{e}}}m→∞lim(1−m1)m=e1
有:
(1−1m)k=((1−1m)m)k/m≈e−k/m{\displaystyle \left(1-{\frac {1}{m}}\right)^{k}=\left(\left(1-{\frac {1}{m}}\right)^{m}\right)^{k/m}\approx e^{-k/m}}(1−m1)k=((1−m1)m)k/m≈e−k/m
添加n个元素某个位置不置为1的概率:
(1−1m)kn≈e−kn/m{\displaystyle \left(1-{\frac {1}{m}}\right)^{kn}\approx e^{-kn/m}}(1−m1)kn≈e−kn/m
添加n个元素某个位置置为1的概率:
1−(1−1m)kn≈1−e−kn/m{\displaystyle 1-\left(1-{\frac {1}{m}}\right)^{kn}\approx 1-e^{-kn/m}}1−(1−m1)kn≈1−e−kn/m
k次hash后误判的概率为:不应置1的置为1的概率
(某个元素判定:k个hash位:全为0一定不存在,全为1可能存在,因此,置为1是可能的概率,因为最初状态全部置为0)
ε=(1−[1−1m]kn)k≈(1−e−kn/m)k{\displaystyle \varepsilon =\left(1-\left[1-{\frac {1}{m}}\right]^{kn}\right)^{k}\approx \left(1-e^{-kn/m}\right)^{k}}ε=(1−[1−m1]kn)k≈(1−e−kn/m)k
由误判率公式可知,当n增加时,误判率增加,m增加时,误判率减少。
下面推导一下hash次数与误判率的关系,令:
f(k)=(1−e−kn/m)kf(k)=\left(1-e^{-kn/m}\right)^{k}f(k)=(1−e−kn/m)k
等式两边取ln对数,有:
ln(f(k))=k∗ln(1−e−kn/m)kln(f(k))=k*ln\left(1-e^{-kn/m}\right)^{k}ln(f(k))=k∗ln(1−e−kn/m)k
求导:
1f(k)f′(k)=ln(1−e−kn/m)k+−knme−kn/m1−e−kn/m\frac{1}{f(k)}f^{'}(k)=ln\left(1-e^{-kn/m}\right)^{k}+\frac{-k\frac{n}{m}e^{-kn/m}}{1-e^{-kn/m}}f(k)1f′(k)=ln(1−e−kn/m)k+1−e−kn/m−kmne−kn/m
若f′(k)=0f^{'}(k)=0f′(k)=0,有:
−knme−kn/m=(1−e−kn/m)ln(1−e−kn/m)k-k\frac{n}{m}e^{-kn/m}=(1-e^{-kn/m})ln\left(1-e^{-kn/m}\right)^{k}−kmne−kn/m=(1−e−kn/m)ln(1−e−kn/m)k
转化一下形式,有:
e−kn/mln(e−kn/m)=(1−e−kn/m)ln(1−e−kn/m)ke^{-kn/m}ln(e^{-kn/m})=(1-e^{-kn/m})ln\left(1-e^{-kn/m}\right)^{k}e−kn/mln(e−kn/m)=(1−e−kn/m)ln(1−e−kn/m)k
于是,有:
e−kn/m=1−e−kn/me^{-kn/m}=1-e^{-kn/m}e−kn/m=1−e−kn/m
e−kn/m=1/2e^{-kn/m}=1/2e−kn/m=1/2
k=mnln2k=\frac{m}{n}ln2k=nmln2
即,k=mnln2k=\frac{m}{n}ln2k=nmln2时,误差率f(k)=(1−e−kn/m)kf(k)=\left(1-e^{-kn/m}\right)^{k}f(k)=(1−e−kn/m)k取得极值,由f(x)=(1−e−k)k>0f(x)=\left(1-e^{-k}\right)^{k}>0f(x)=(1−e−k)k>0可知,
(0, mnln2\frac{m}{n}ln2nmln2]时,f′(k)<0f^{'}(k)<0f′(k)<0
(mnln2,+∞\frac{m}{n}ln2, +\inftynmln2,+∞]时,f′(k)<0f^{'}(k)<0f′(k)<0
由此可知,当k=mnln2k=\frac{m}{n}ln2k=nmln2时是f(k)f(k)f(k)的最小值,即误判率最小。
通过函数图像模拟不同情况的曲线:
f(k)=(1−e−k)kf(k)=\left(1-e^{-k}\right)^{k}f(k)=(1−e−k)k
f(k)=(1−e−2k)kf(k)=\left(1-e^{-2k}\right)^{k}f(k)=(1−e−2k)k
f(k)=(1−e−3k)kf(k)=\left(1-e^{-3k}\right)^{k}f(k)=(1−e−3k)k
这里取m=1,n分别为1,2,3,
函数曲线如下图所示,由图可知,
误差率(误判率)有最小值,并且,当n增加时,误判率增加,m增加时,误判率减少(控制变量法:hash次数相同)。
绘图工具网站:https://zh.numberempire.com/graphingcalculator.php

4小结
(1)布隆过滤器的误差率为:f(k)=(1−e−kn/m)kf(k)=\left(1-e^{-kn/m}\right)^{k}f(k)=(1−e−kn/m)k;
(2)布隆过滤器最小误判率对应的hash次数与布隆过滤器与数据插入量的关系:k=mnln2k=\frac{m}{n}ln2k=nmln2,其中,k为hash次数,m布隆过滤器长度,n插入数据量;
(3)当n增加时,误判率增加,m增加时,误判率减少。
相关文章:

Redis进阶:布隆过滤器(Bloom Filter)及误判率数学推导
1 缘起 有一次偶然间听到有同事在说某个项目中使用了布隆过滤器, 哎呦,我去,我竟然不知道啥是布隆过滤器, 这我哪能忍?其实,也可以忍,但是,可能有的面试官不能忍!&#…...
Java创建对象的方式
Java创建对象的五种方式: (1)使用new关键字 (2)使用Object类的clone方法 (3)使用Class类的newInstance方法 (4)使用Constructor类中的newInstance方法 (5&am…...

dom基本操作
1、style修改样式 基本语法: 元素.style.样式’值‘ 注意: 1.修改样式通过style属性引出 2.如果属性有-连接符,需要转换为小驼峰命名法 3.赋值的时候,需要的时候不要忘记加css单位 4.后面的值必须是字符串 <div></div> // 1、…...

如何将python训练的XGBoost模型部署在C++环境推理
当前环境:Ubuntu,xgboost1.7.4过程介绍:首先用python训练XGBoost模型,在训练完成后注意使用xgb_model.save_model(checkpoint.model)进行模型的保存。找到xgboost的动态链接库和头文件动态链接库:如果你在conda环境下面…...
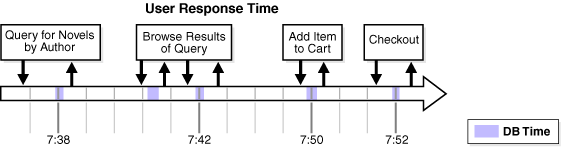
About Oracle Database Performance Method
bottleneck(瓶颈): a point where resource contention is highest throughput(吞吐量): the amount of work that can be completed in a specified time. response time (响应时间): the time to complete a spec…...
)
JavaScript 日期和时间的格式化大汇总(收集)
一、日期和时间的格式化 1、原生方法 1.1、使用 toLocaleString 方法 Date 对象有一个 toLocaleString 方法,该方法可以根据本地时间和地区设置格式化日期时间。例如: const date new Date(); console.log(date.toLocaleString(en-US, { timeZone: …...
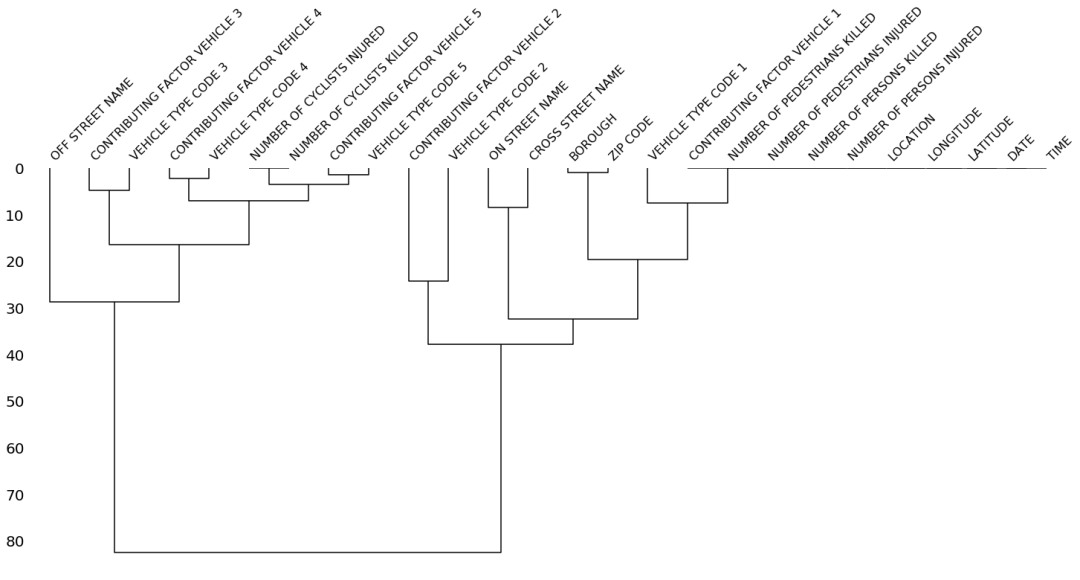
【Python】缺失值可视化工具库:missingno
文章目录一、前言二、下载二、使用介绍2.1 绘制缺失值条形图2.2 绘制缺失值热力图2.3 缺失值树状图三、参考资料一、前言 在我们进行机器学习或者深度学习的时候,我们经常会遇到需要处理数据集缺失值的情况,那么如何可视化数据集的缺失情况呢࿱…...

【代码随想录二刷】Day18-二叉树-C++
代码随想录二刷Day18 今日任务 513.找树左下角的值 112.路径总和 113.路径总和ii 106.从中序与后序遍历序列构造二叉树 105.从前序与中序遍历序列构造二叉树 语言:C 513.找树左下角的值 链接:https://leetcode.cn/problems/find-bottom-left-tree-va…...
制造业的云ERP在外网怎么访问?内网服务器一步映射到公网
随着企业信息化、智能化时代的到来,很多制造业企业都在用云ERP。用友U 9cloud通过双版本公有云专属、私有云订阅、传统软件购买三种模式满足众多制造业企业的需求,成为一款适配中型及中大型制造业的云ERP,是企业数智制造的创新平台。 用友U 9…...

zookeeper 复习 ---- 练习
zookeeper 复习 ---- 练习在同一节点配置三个 zookeeper,配置正确的是? A: zoo1.cfg tickTime2000 initLimit5 syncLimit2 dataDir/var/lib/zookeeper/zoo1 clientPort2181 server.1localhost:2666:3666 server.2localhost:2667:3667 serv…...

2023年全国最新道路运输从业人员精选真题及答案1
百分百题库提供道路运输安全员考试试题、道路运输从业人员考试预测题、道路安全员考试真题、道路运输从业人员证考试题库等,提供在线做题刷题,在线模拟考试,助你考试轻松过关。 11.在以下选项中关于安全生产管理方针描述正确的是(…...
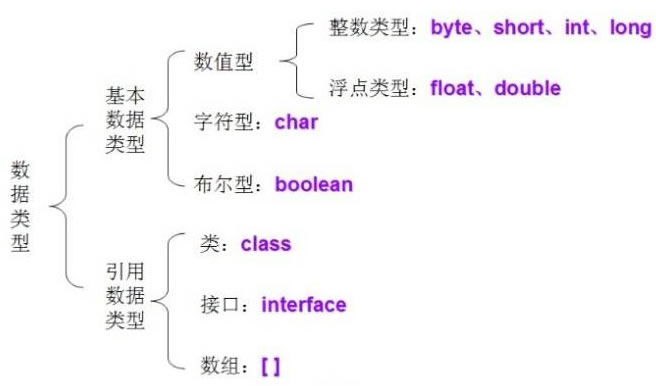
Java每日一练——Java简介与基础练习
系列文章目录 提示:这里可以添加系列文章的所有文章的目录,目录需要自己手动添加 例如:第一章 Python 机器学习入门之pandas的使用 文章目录 目录 系列文章目录 文章目录 前言 一、简述解释型语言与编译型语言 二、Java语言的执行流程 2.1、…...
解决Edge浏览器主页被篡改问题,或许可以帮你彻底解决
问题描述: 之前从一个第三方网站下载了一个不知名软件,接着电脑就各种下载360全家桶之类的软件,后来问题解决了,但是还残留了一些问题,前几天发现edge浏览器的主页被改成了360导航,就是那个该死的hao123&a…...
字符设备驱动基础(一)
目录 一、Linux内核对设备的分类 linux的文件种类: Linux内核按驱动程序实现模型框架的不同,将设备分为三类: 总体框架图: 二、设备号------内核中同类设备的区分 三、申请和注销设备号 四、函数指针复习 4.1、 内存四区 …...
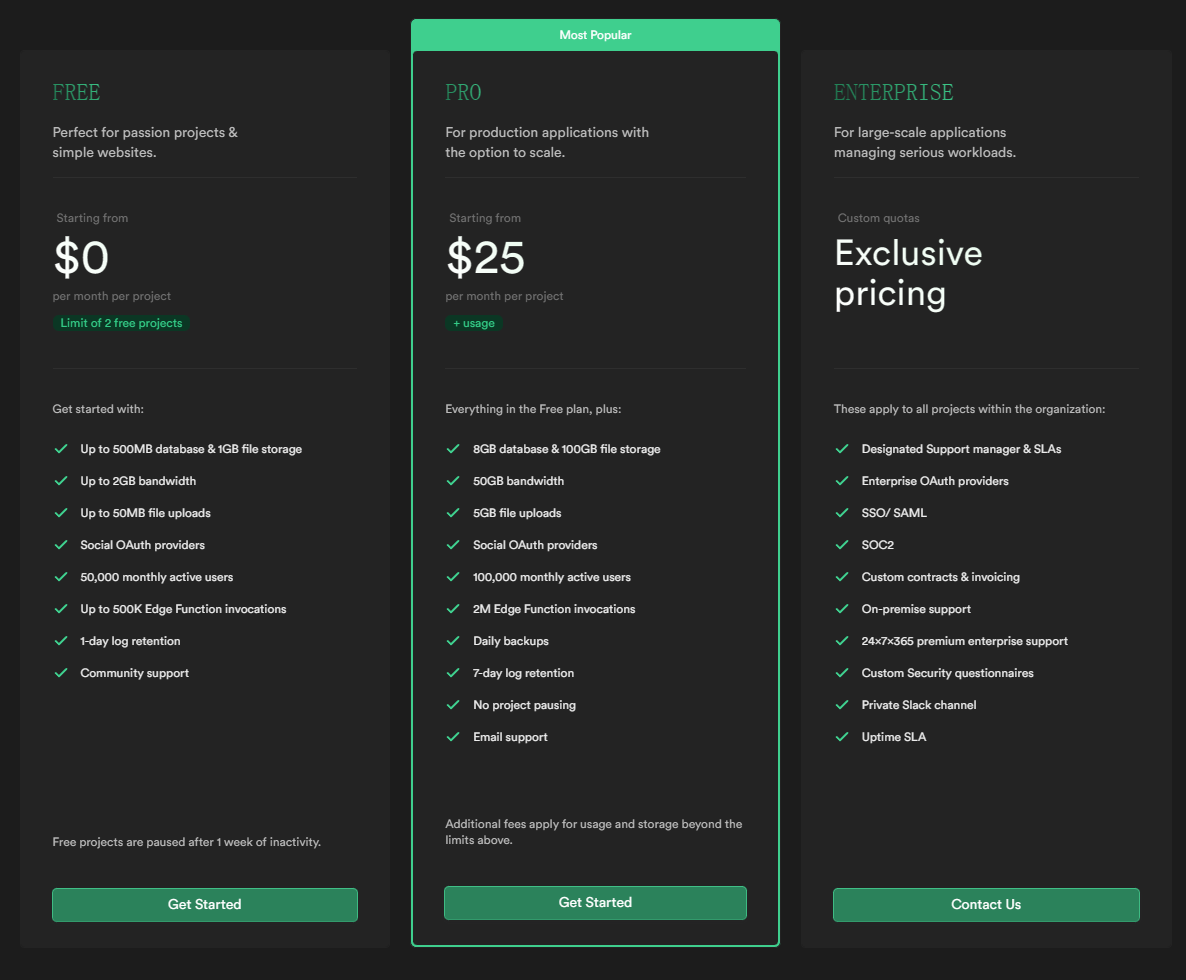
将 Supabase 作为下一个后端服务
对于想快速实现一个产品而言,如果使用传统开发,又要兼顾前端开发,同时又要花费时间构建后端服务。然而有这么一个平台(Baas Backend as a service)后端即服务,能够让开发人员可以专注于前端开发,…...

14:高级篇 - CTK 服务工厂 简述
作者: 一去、二三里 个人微信号: iwaleon 微信公众号: 高效程序员 一般情况下,服务对象在被注册之后,任何其它的 Plugin 在请求该服务时,CTK Plugin Framework 都返回的是同一个对象。倘若要为每一个 Plugin 消费者返回不同的服务对象,或者在真正需要该服务对象时才创建…...
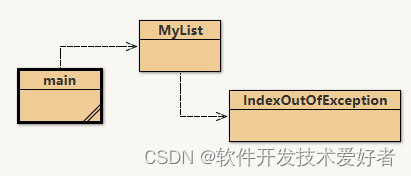
Java中的链表实现介绍
Java中的链表实现介绍 学习数据结构的的链表和树时,会遇到节点(node)和链表(linked list)这两个术语,节点是处理数据结构的链表和树的基础。节点是一种数据元素,包括两个部分:一个是…...
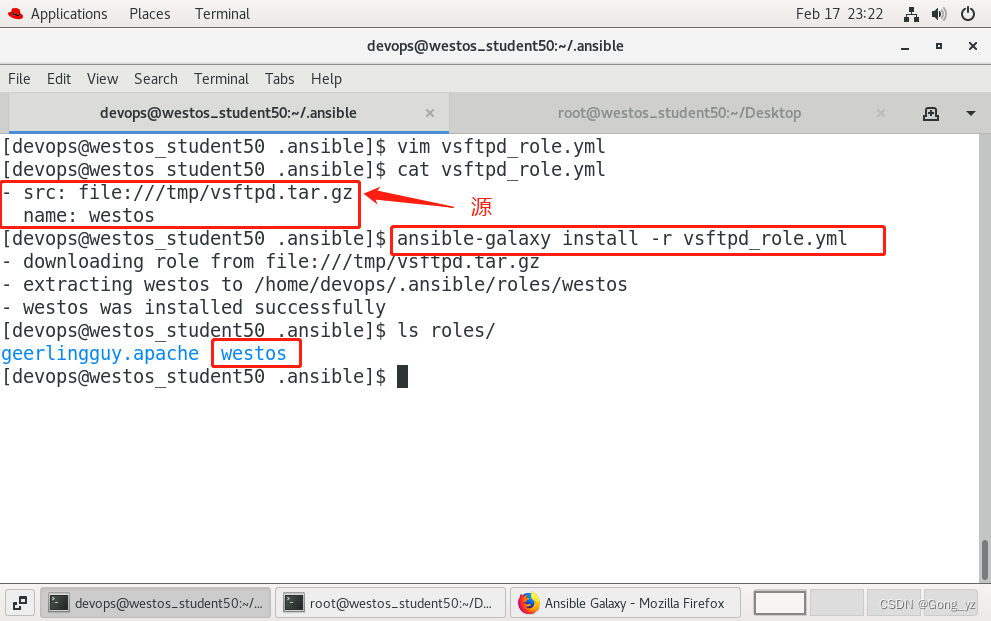
演示Ansible中的角色使用方法(ansible roles)
文章目录一、ansible 角色简介二、roles目录结构三、role存放的路径:配置文件ansible.cfg中定义四、创建目录结构五、playbook中使用rolesplaybook变量会覆盖roles中的定义变量六、控制任务执行顺序七、ansible—galaxy命令工具八、安装选择的角色1.从网上下载&…...
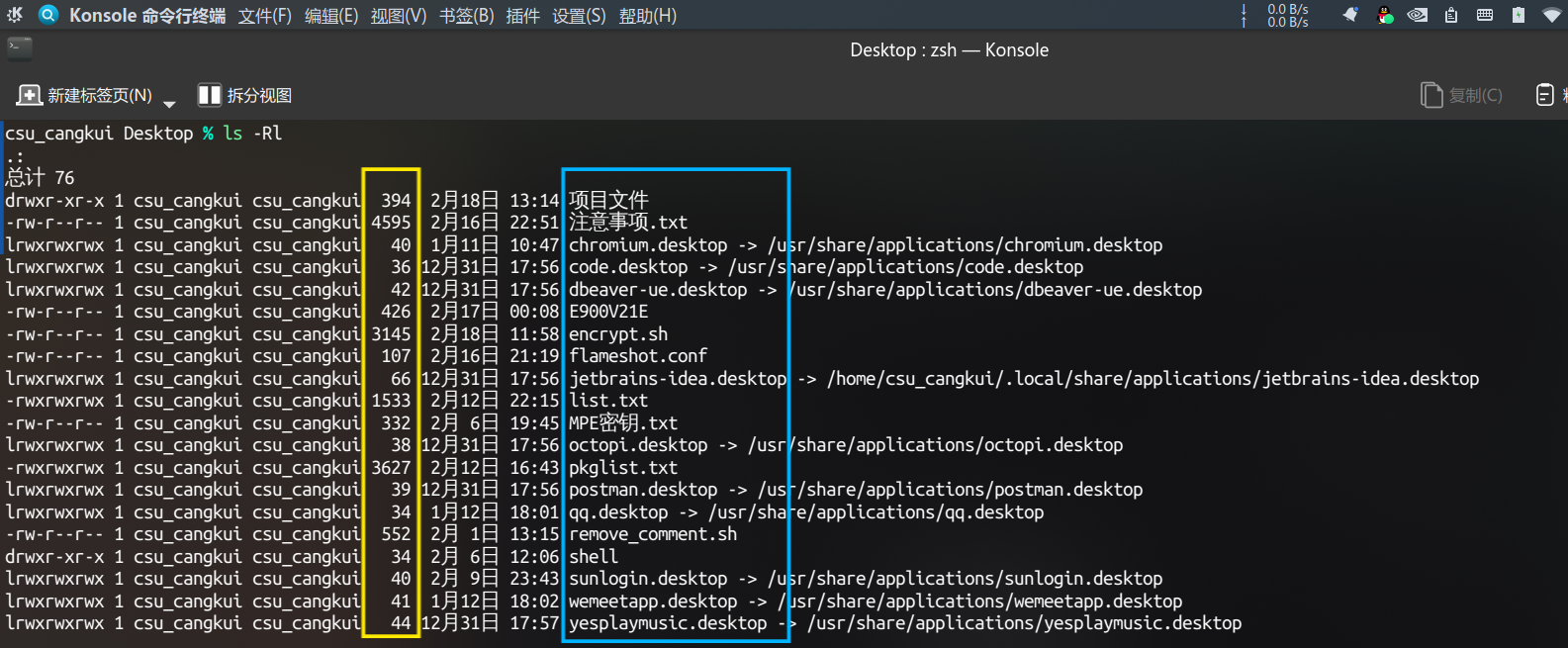
Bash Shell 通过ls命令筛选文件
Bash Shell 通过ls命令及其管道根据大小名称筛选文件 最近参与的项目当中有需要用pyarmor加密项目的要求,听网上吹的pyarmor都那么神,用了一下感觉也一般,试用版普通模式下文件加密居然还有大小32KB的限制,加密到一半就失败了&am…...

2023-2-18 刷题情况
删列造序 III 题目描述 给定由 n 个小写字母字符串组成的数组 strs ,其中每个字符串长度相等。 选取一个删除索引序列,对于 strs 中的每个字符串,删除对应每个索引处的字符。 比如,有 strs [“abcdef”,“uvwxyz”] …...

Chapter03-Authentication vulnerabilities
文章目录 1. 身份验证简介1.1 What is authentication1.2 difference between authentication and authorization1.3 身份验证机制失效的原因1.4 身份验证机制失效的影响 2. 基于登录功能的漏洞2.1 密码爆破2.2 用户名枚举2.3 有缺陷的暴力破解防护2.3.1 如果用户登录尝试失败次…...

OpenLayers 可视化之热力图
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 热力图(Heatmap)又叫热点图,是一种通过特殊高亮显示事物密度分布、变化趋势的数据可视化技术。采用颜色的深浅来显示…...

【Linux】C语言执行shell指令
在C语言中执行Shell指令 在C语言中,有几种方法可以执行Shell指令: 1. 使用system()函数 这是最简单的方法,包含在stdlib.h头文件中: #include <stdlib.h>int main() {system("ls -l"); // 执行ls -l命令retu…...

【Web 进阶篇】优雅的接口设计:统一响应、全局异常处理与参数校验
系列回顾: 在上一篇中,我们成功地为应用集成了数据库,并使用 Spring Data JPA 实现了基本的 CRUD API。我们的应用现在能“记忆”数据了!但是,如果你仔细审视那些 API,会发现它们还很“粗糙”:有…...

【git】把本地更改提交远程新分支feature_g
创建并切换新分支 git checkout -b feature_g 添加并提交更改 git add . git commit -m “实现图片上传功能” 推送到远程 git push -u origin feature_g...
多光源(Multiple Lights))
C++.OpenGL (14/64)多光源(Multiple Lights)
多光源(Multiple Lights) 多光源渲染技术概览 #mermaid-svg-3L5e5gGn76TNh7Lq {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-3L5e5gGn76TNh7Lq .error-icon{fill:#552222;}#mermaid-svg-3L5e5gGn76TNh7Lq .erro…...

Qwen系列之Qwen3解读:最强开源模型的细节拆解
文章目录 1.1分钟快览2.模型架构2.1.Dense模型2.2.MoE模型 3.预训练阶段3.1.数据3.2.训练3.3.评估 4.后训练阶段S1: 长链思维冷启动S2: 推理强化学习S3: 思考模式融合S4: 通用强化学习 5.全家桶中的小模型训练评估评估数据集评估细节评估效果弱智评估和民间Arena 分析展望 如果…...

使用ch340继电器完成随机断电测试
前言 如图所示是市面上常见的OTA压测继电器,通过ch340串口模块完成对继电器的分路控制,这里我编写了一个脚本方便对4路继电器的控制,可以设置开启时间,关闭时间,复位等功能 软件界面 在设备管理器查看串口号后&…...

Yolo11改进策略:Block改进|FCM,特征互补映射模块|AAAI 2025|即插即用
1 论文信息 FBRT-YOLO(Faster and Better for Real-Time Aerial Image Detection)是由北京理工大学团队提出的专用于航拍图像实时目标检测的创新框架,发表于AAAI 2025。论文针对航拍场景中小目标检测的核心难题展开研究,重点解决…...

使用python进行图像处理—图像变换(6)
图像变换是指改变图像的几何形状或空间位置的操作。常见的几何变换包括平移、旋转、缩放、剪切(shear)以及更复杂的仿射变换和透视变换。这些变换在图像配准、图像校正、创建特效等场景中非常有用。 6.1仿射变换(Affine Transformation) 仿射变换是一种…...
