【二叉树】1-5,理论基础、前中后序遍历的递归法和迭代法、层序遍历
理论基础、前中后序遍历的递归法和迭代法、层序遍历
- 1,二叉树的种类
- 满二叉树
- 完全二叉树
- 二叉搜索树
- 平衡二叉搜索树
- 2,存储方式
- 链式存储
- 线式存储
- 3,二叉树的遍历
- 深度优先搜索
- 前序遍历(递归法、迭代法)
- 中序遍历(递归法、迭代法)
- 后序遍历(递归法、迭代法)
- 广度优先搜索
- 层次遍历(迭代法、递归法)
- 4,二叉树的定义
1,二叉树的种类
满二叉树
除最后一层无任何子节点外,每一层上的所有结点都有两个子结点的二叉树。
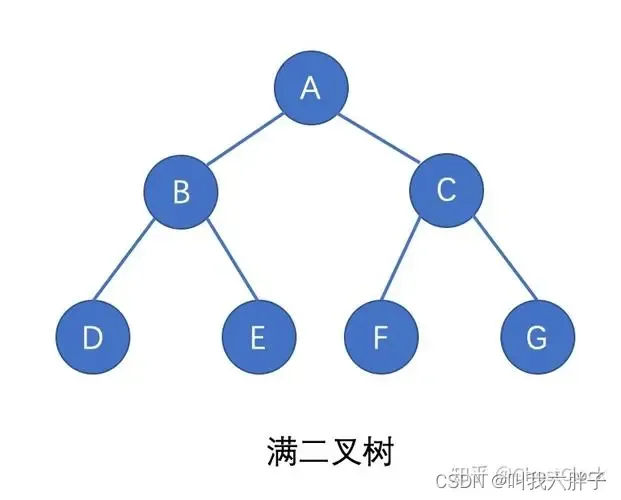
完全二叉树
一个深度为k的有n个节点的二叉树,对树中的节点按从上至下、从左到右的顺序进行编号,如果编号为i(1≤i≤n)的结点与满二叉树中编号为i的结点在二叉树中的位置相同,则这棵二叉树称为完全二叉树。

二叉搜索树
二叉搜索树(Binary Search Tree),又名二叉排序树(Binary Sort Tree)。
二叉搜索树是具有有以下性质的二叉树:
若左子树不为空,则左子树上所有节点的值均小于或等于它的根节点的值。
若右子树不为空,则右子树上所有节点的值均大于或等于它的根节点的值。
左、右子树也分别为二叉搜索树。
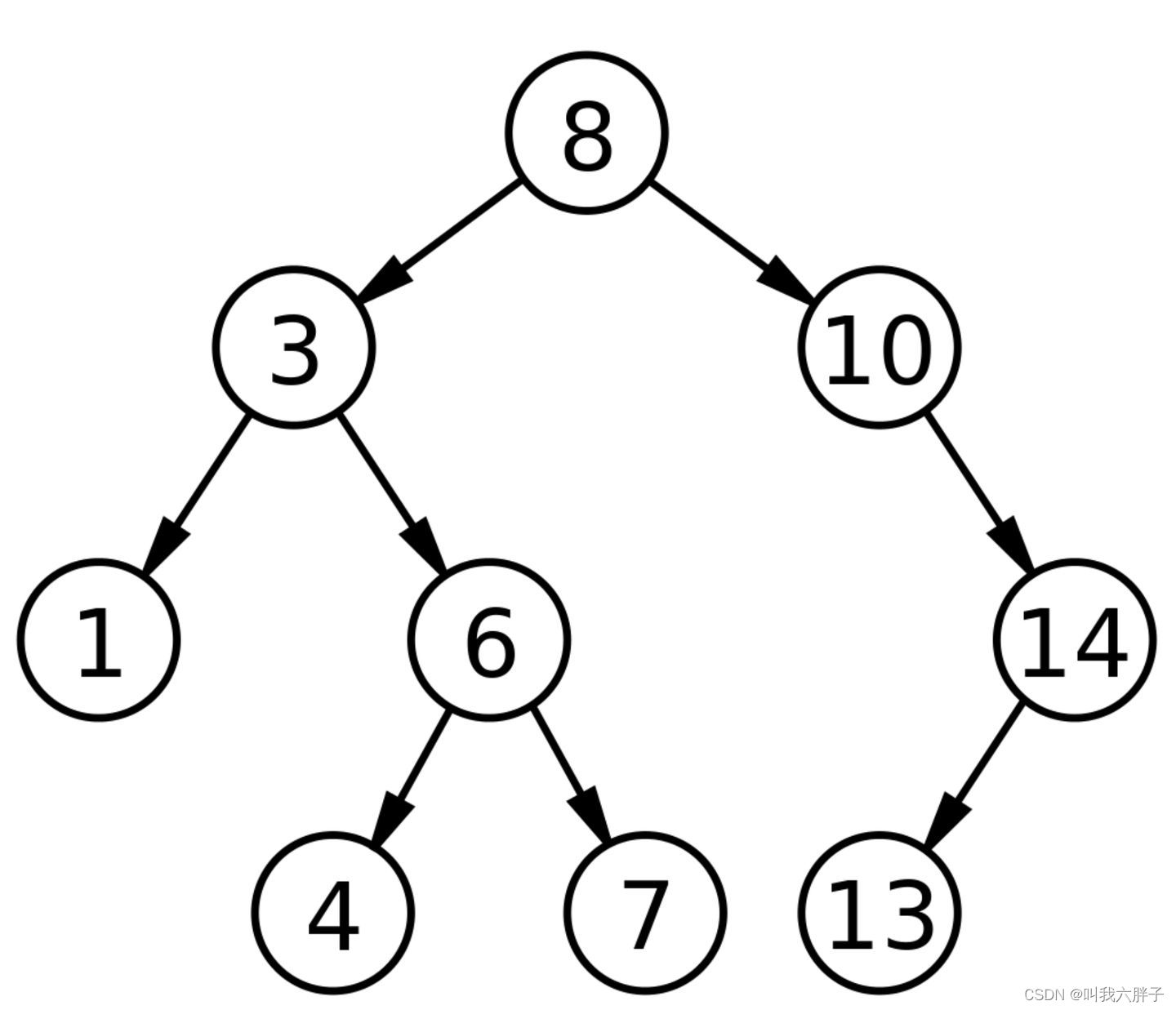
平衡二叉搜索树
平衡二叉搜索树的任何结点的左子树和右子树高度最多相差1。,并且左右两个子树都是一棵平衡二叉树。
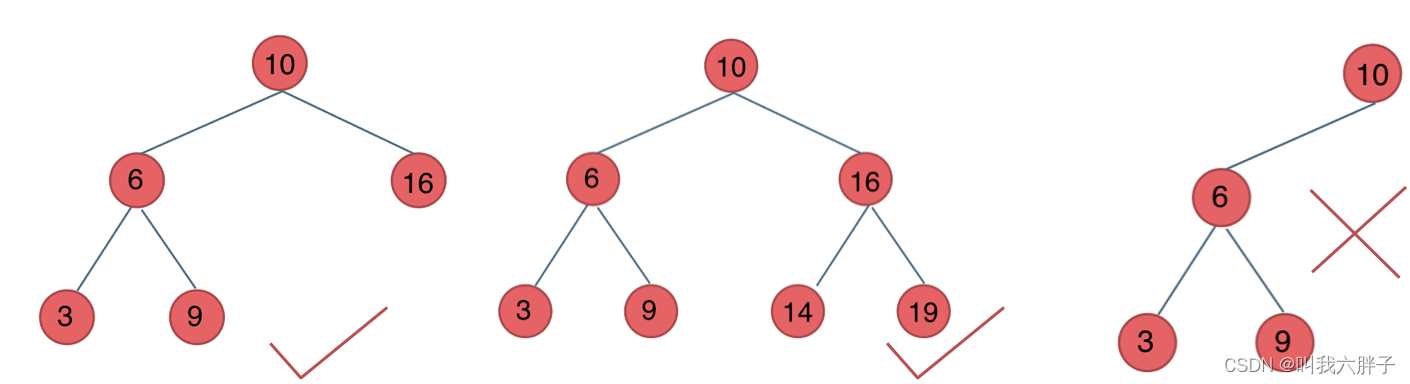
容器map、set、multimap、multiset的底层原理都是平衡二叉搜索树
所以map中key和set中的元素都是有序的
unordered map和unordered set的底层原理为哈希表
2,存储方式
分为链式存储和线式存储
链式存储
链式存储方式就用指针
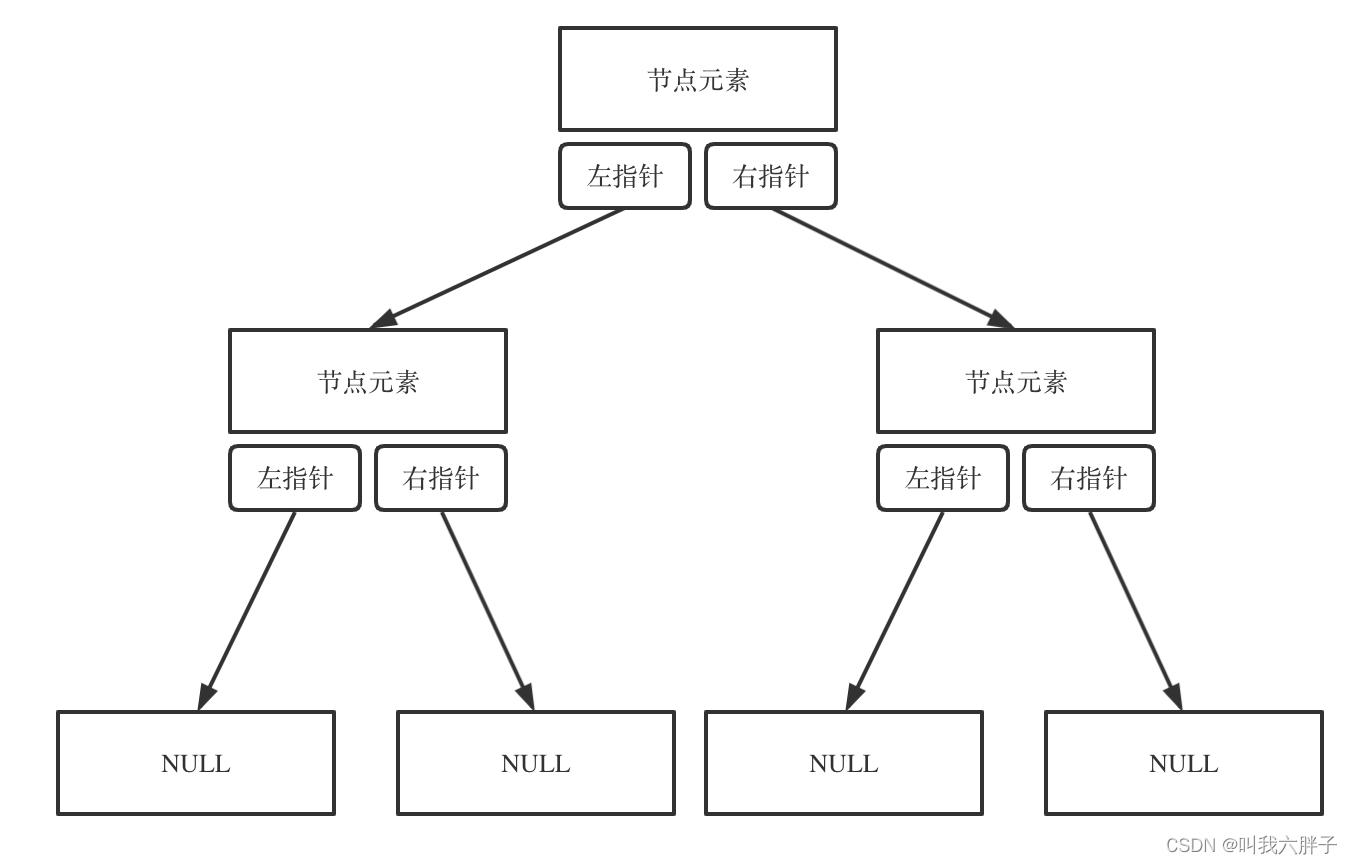
线式存储
(用的少了解即可)
顺序存储的方式就是用数组。
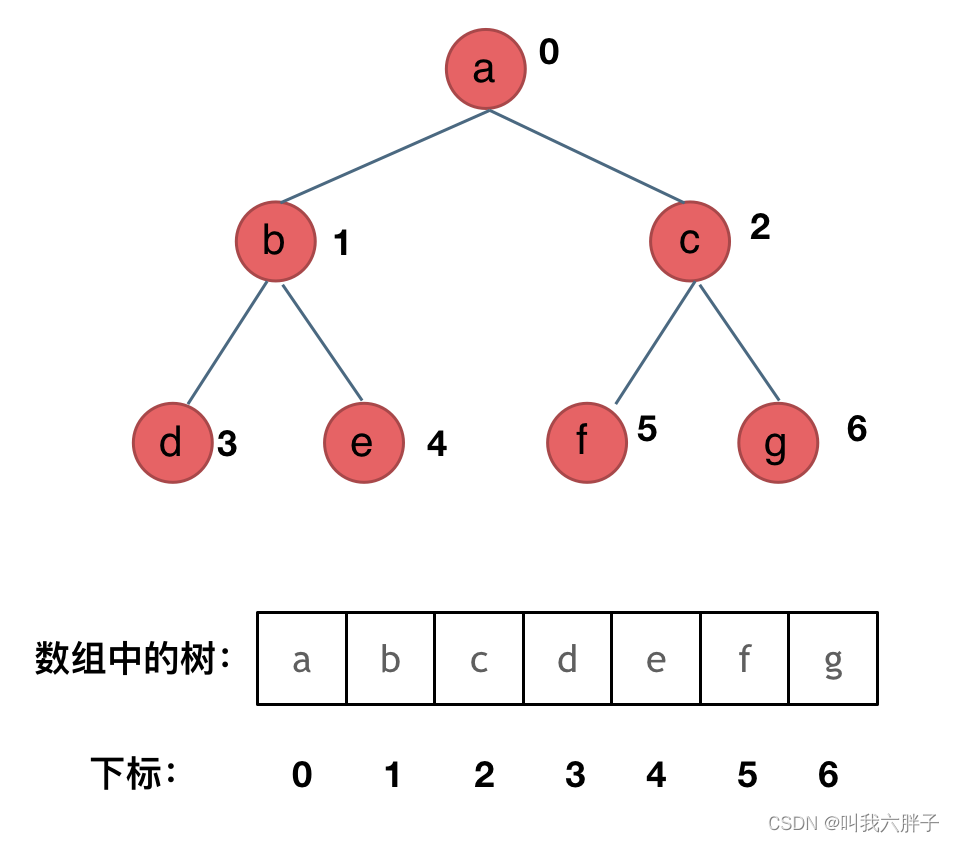
线式存储时,有一点i,他的左孩子下标为2i+1,他的右孩子下标为2i+2
3,二叉树的遍历
分为深度优先搜索和广度优先搜索
深度优先搜索
分为前序遍历、中序遍历、后续遍历
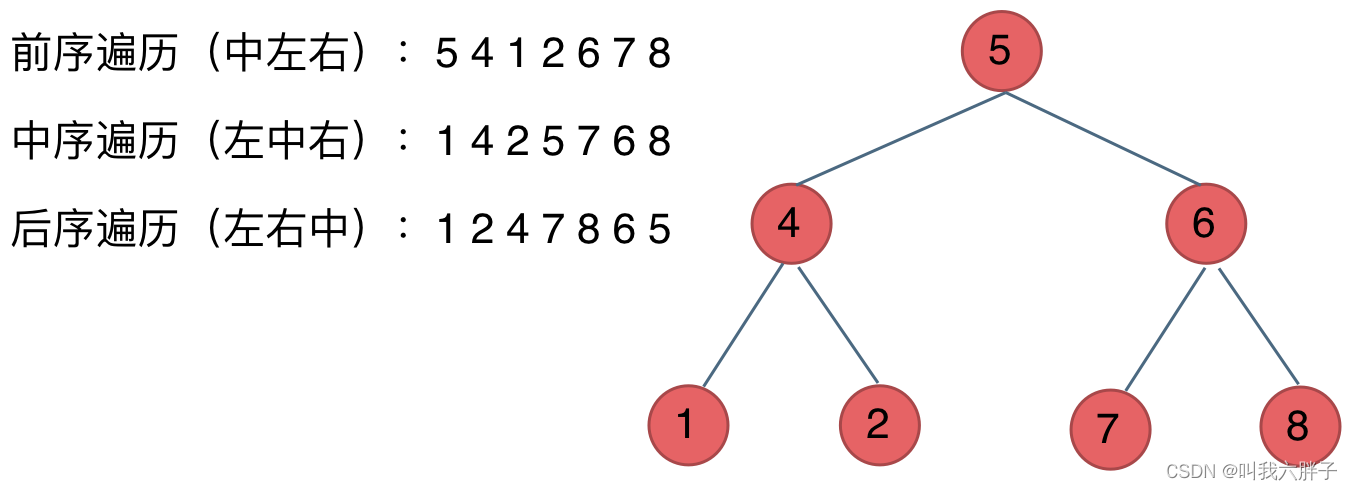
写法可以分为递归法和迭代法
递归的底层原理是栈
确定递归函数的参数和返回值
确定终止条件
确定单层递归的逻辑
迭代法就是模拟递归的过程,因为递归的底层原理为栈,所以迭代法用栈展示
面试简单的可能需要写出简单的非递归代码
前序遍历(递归法、迭代法)
中左右
递归法:
class Solution {
public:void traversal(TreeNode* cur, vector<int>& vec) {if (cur == NULL) return;vec.push_back(cur->val); // 中traversal(cur->left, vec); // 左traversal(cur->right, vec); // 右}vector<int> preorderTraversal(TreeNode* root) {vector<int> result;traversal(root, result);return result;}
};
迭代法:
因为模拟栈的过程,前序遍历是中左右,但是栈是先进后出的,所以入栈顺序为右左中
访问顺序和处理顺序相同(后续遍历也是如此,所以稍作改动就可以变为后续遍历)
class Solution {
public:vector<int> preorderTraversal(TreeNode* root) {stack<TreeNode*> st;vector<int> result;if (root == NULL) return result;st.push(root);while (!st.empty()) {TreeNode* node = st.top(); // 中st.pop();result.push_back(node->val);if (node->right) st.push(node->right); // 右(空节点不入栈)if (node->left) st.push(node->left); // 左(空节点不入栈)}return result;}
};
中序遍历(递归法、迭代法)
左中右
递归法:
void traversal(TreeNode* cur, vector<int>& vec) {if (cur == NULL) return;traversal(cur->left, vec); // 左vec.push_back(cur->val); // 中traversal(cur->right, vec); // 右
}
迭代法:
访问顺序和处理顺序不同,所以代码和前后续遍历不同
class Solution {
public:vector<int> inorderTraversal(TreeNode* root) {vector<int> result;stack<TreeNode*> st;TreeNode* cur = root;while (cur != NULL || !st.empty()) {if (cur != NULL) { // 指针来访问节点,访问到最底层st.push(cur); // 将访问的节点放进栈cur = cur->left; // 左} else {cur = st.top(); // 从栈里弹出的数据,就是要处理的数据(放进result数组里的数据)st.pop();result.push_back(cur->val); // 中cur = cur->right; // 右}}return result;}
};
后序遍历(递归法、迭代法)
左右中
递归法:
void traversal(TreeNode* cur, vector<int>& vec) {if (cur == NULL) return;traversal(cur->left, vec); // 左traversal(cur->right, vec); // 右vec.push_back(cur->val); // 中
}
迭代法:
访问顺序和处理顺序相同
class Solution {
public:vector<int> postorderTraversal(TreeNode* root) {stack<TreeNode*> st;vector<int> result;if (root == NULL) return result;st.push(root);while (!st.empty()) {TreeNode* node = st.top();st.pop();result.push_back(node->val);if (node->left) st.push(node->left); // 相对于前序遍历,这更改一下入栈顺序 (空节点不入栈)if (node->right) st.push(node->right); // 空节点不入栈}reverse(result.begin(), result.end()); // 将结果反转之后就是左右中的顺序了return result;}
};
广度优先搜索
层次遍历(迭代法、递归法)
借助一个队列,保存每一层的节点
队列记录当前层的元素个数,弹出时按队列里储存的个数弹出
迭代法:
class Solution {
public:vector<vector<int>> levelOrder(TreeNode* root) {queue<TreeNode*> que;if (root != NULL) que.push(root);vector<vector<int>> result;while (!que.empty()) {int size = que.size();vector<int> vec;// 这里一定要使用固定大小size,不要使用que.size(),因为que.size是不断变化的for (int i = 0; i < size; i++) {TreeNode* node = que.front();que.pop();vec.push_back(node->val);if (node->left) que.push(node->left);if (node->right) que.push(node->right);}result.push_back(vec);}return result;}
};
递归法:
class Solution {
public:void order(TreeNode* cur, vector<vector<int>>& result, int depth){if (cur == nullptr) return;if (result.size() == depth) result.push_back(vector<int>());result[depth].push_back(cur->val);order(cur->left, result, depth + 1);order(cur->right, result, depth + 1);}vector<vector<int>> levelOrder(TreeNode* root) {vector<vector<int>> result;int depth = 0;order(root, result, depth);return result;}
};
4,二叉树的定义
struct TreeNode {int val;TreeNode *left;TreeNode *right;TreeNode(int x) : val(x), left(NULL), right(NULL) {}
};
相关文章:

【二叉树】1-5,理论基础、前中后序遍历的递归法和迭代法、层序遍历
理论基础、前中后序遍历的递归法和迭代法、层序遍历 1,二叉树的种类满二叉树完全二叉树二叉搜索树平衡二叉搜索树 2,存储方式链式存储线式存储 3,二叉树的遍历深度优先搜索前序遍历(递归法、迭代法)中序遍历࿰…...

Mybatis-plus动态条件查询QueryWrapper的使用
Mybatis-plus动态条件查询QueryWrapper的使用 一:queryWrapper介绍 queryWrapper是mybatis plus中实现查询的对象封装操作类,可以封装sql对象,包括where条件,order by排序,select哪些字段等等,他的层级关…...
Redis安装配置远程连接
1. yum 安装 redis: 直接使用命令,将 redis 安装到 linux 服务器中: yum -y install redis 2. 启动 redis: 在 xshell 里,可以使用下面命令,以后台方式启动 redis: [rootVM-8-17-centos /]…...
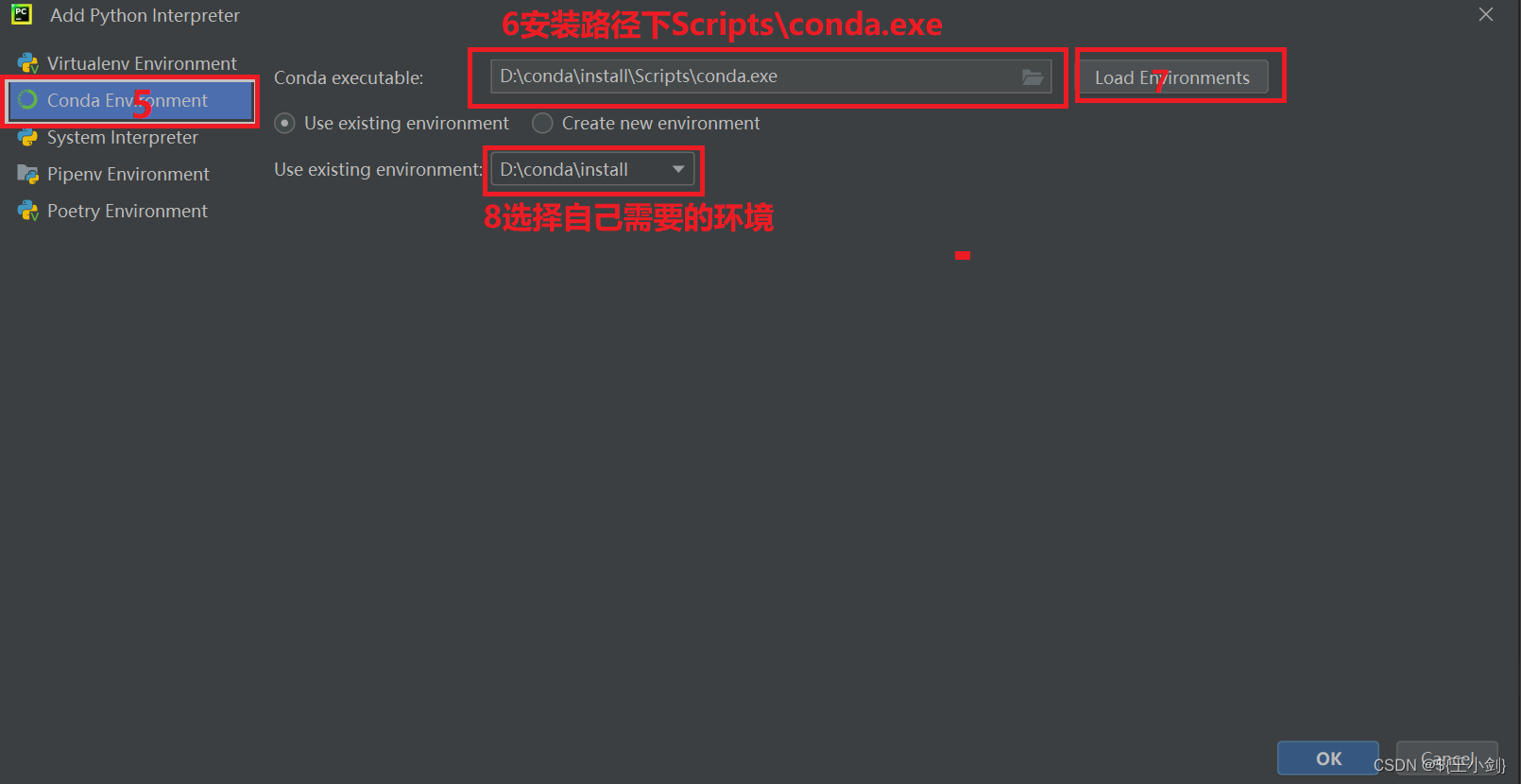
pycharm中配置conda
安装好pycharm和conda后,打开pycharm:...
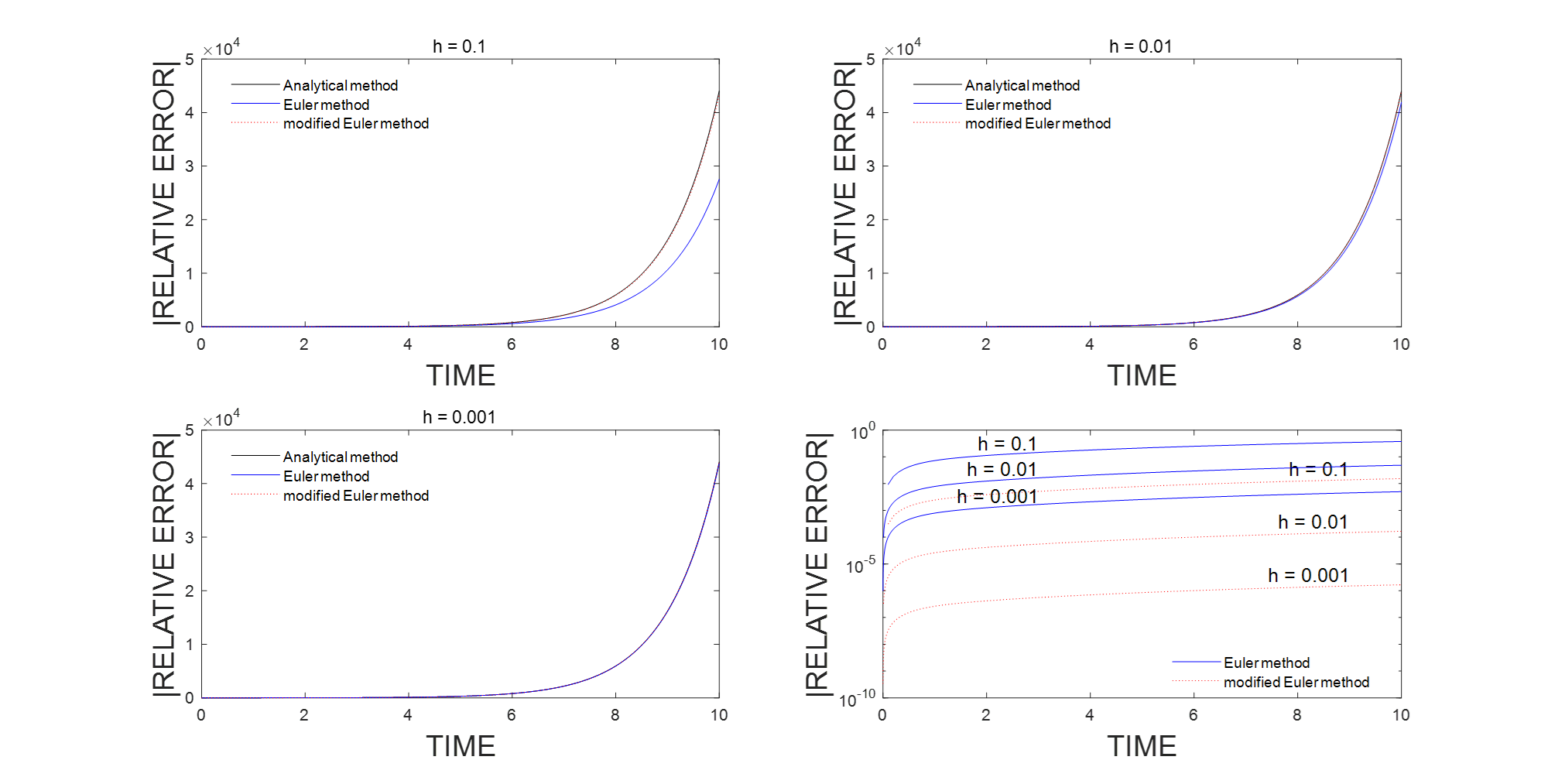
matlab解常微分方程常用数值解法1:前向欧拉法和改进的欧拉法
总结和记录一下matlab求解常微分方程常用的数值解法,本文先从欧拉法和改进的欧拉法讲起。 d x d t f ( x , t ) , x ( t 0 ) x 0 \frac{d x}{d t}f(x, t), \quad x\left(t_{0}\right)x_{0} dtdxf(x,t),x(t0)x0 1. 前向欧拉法 前向欧拉法使用了泰勒展开的第…...
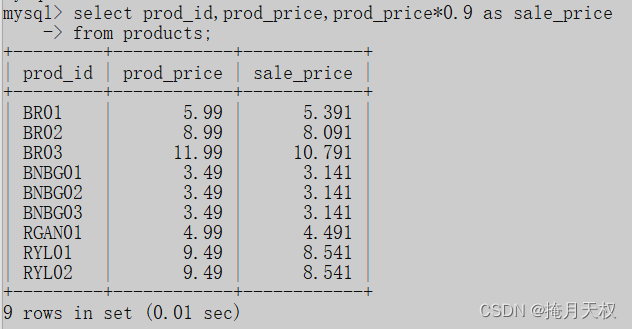
SQL | 计算字段
7-创建计算字段 7.1-计算字段 存储在数据库中的数据一般不是我们所需要的字段格式, 需要公司名称,同时也需要公司地址,但是这两个数据存储在不同的列中。 省,市,县和邮政编码存储在不同的列中,但是当我们…...

leetcode做题笔记67
给你两个二进制字符串 a 和 b ,以二进制字符串的形式返回它们的和。 思路一:模拟题意 void reserve(char* s) {int len strlen(s);for (int i 0; i < len / 2; i) {char t s[i];s[i] s[len - i - 1], s[len - i - 1] t;} }char* addBinary(cha…...
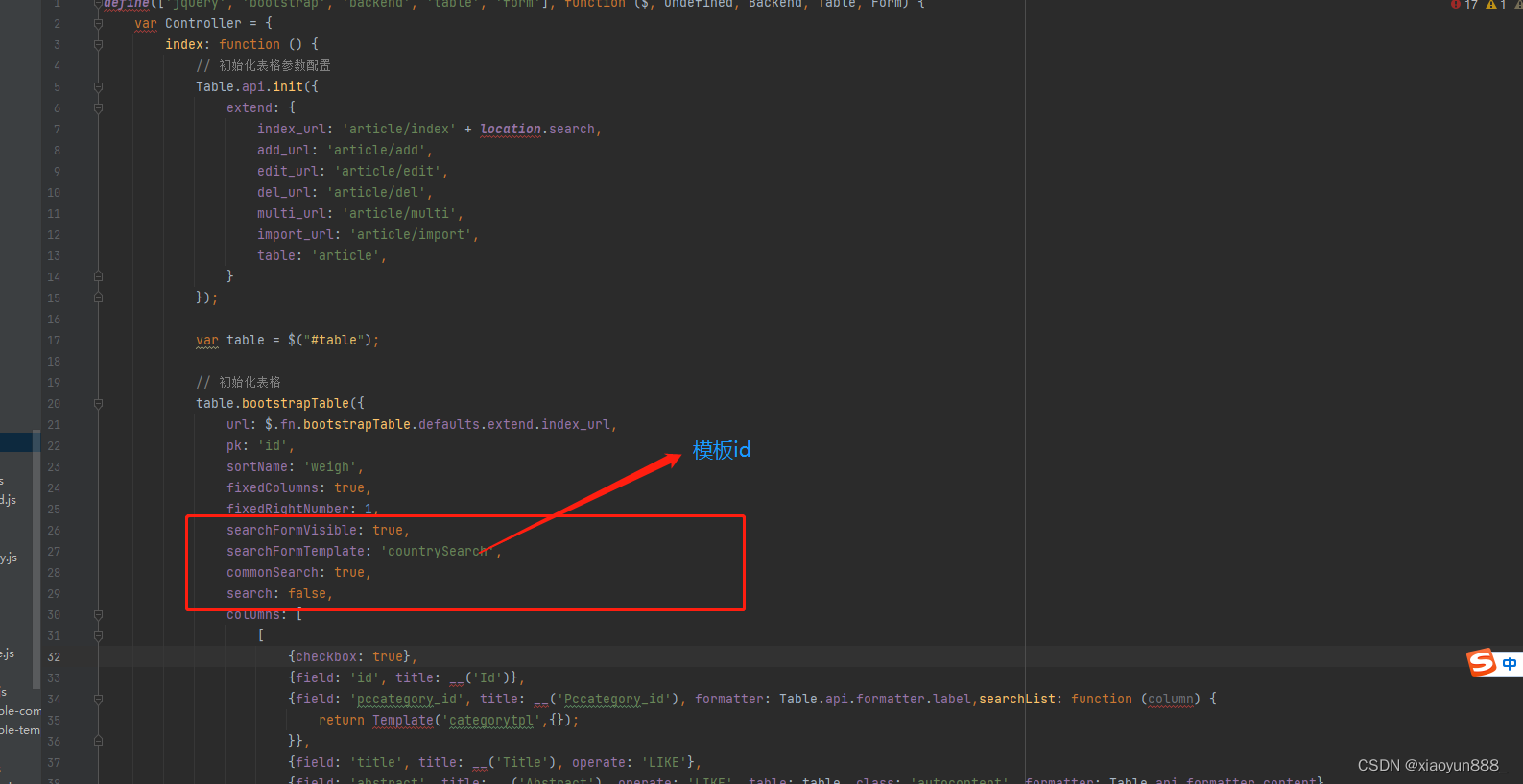
fastadmin 自定义搜索分类和时间范围
1.分类搜索,分类信息获取----php 2.对应html页面,页面底部加搜索提交代码(这里需要注意:红框内容) 图上代码----方便直接复制使用 <script id"countrySearch" type"text/html"><!--form…...

Oracle Data Redaction与Data Pump
如果表定义了Redaction Policy,导出时数据会脱敏吗?本文解答这个问题。 按照Oracle文档Advanced Security Guide第13章,13.6.5的Tutorial,假设表HR.jobs定义了Redaction Policy。 假设HR用户被授予了访问目录对象的权限…...

设计模式(6)原型模式
一、介绍 Java中自带的原型模式是clone()方法。该方法是Object的方法,native类型。他的作用就是将对象的在内存的那一块内存数据一字不差地再复制一个。我们写简单类的时候只需要实现Cloneable接口,然后调用Object::clone方法就可实现克隆功能。这样实现…...

pywinauto结合selenium实现文件上传
简介 PC端-Windows上的元素识别可用viewWizard工具 PC端-Windows上的元素操作可用pywinauto库 浏览器上网页的元素识别可用selenium 安装 pip installer pywinauto 使用须知 pywinauto官方文档 确定app的可访问技术 1、win32 API(backend=“win32”) 一般是MFC、VB6、VC…...
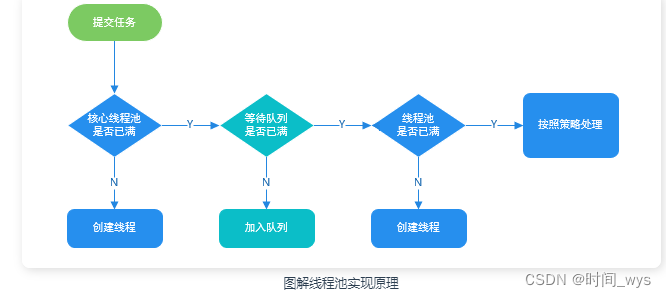
【Java多线程学习7】Java线程池技术
线程池技术 一、什么是线程池 线程池顾名思义是管理一组线程的池子。当有任务要处理时,直接从线程池中获取线程来处理,处理完之后线程不会立即销毁,而是等待下一个任务。 二、为什么要使用线程池? 线程池的作用? 1、降低资源…...
VMware虚拟机NAT模式Ubuntu无法上网解决方案
发现只要NAT模式,ping地址时就报网络不可达,且右上方网络图标消失,但是外部USB网络设备又只能在NAT模式下使用。。。 博主的解决方案如下: 按WinR键入services.msc, 找到VMware DHCP Service、VMware NAT Service和V…...

Linux中无法忘记mysql密码处理办法
找到/etc/my.cnf或者/etc/mysql/my.cnf文件 添加下面两行代码,取消密码验证 [mysqld] skip-grant-table使用命令登录:mysql -u root -p,回车,回车使用sql语句来修改密码 mysql>use mysql; mysql>update user set password…...
)
vue 使用 el-upload 上传文件(自动上传/手动上传)
vue 使用 el-upload 上传文件(自动上传/手动上传) 文章目录 1. 自动上传(选择完文件后,调用axios上传)2.手动上传 1. 自动上传(选择完文件后,调用axios上传) <el-uploadref"upload1"action:multiple"false"accept".xlsx,.csv,.xls":auto-upl…...
服务器遭受攻击之后的常见思路
哈喽大家好,我是咸鱼 不知道大家有没有看过这么一部电影: 这部电影讲述了男主是一个电脑极客,在计算机方面有着不可思议的天赋,男主所在的黑客组织凭借着超高的黑客技术去入侵各种国家机构的系统,并引起了德国秘密警察…...
C语言学习笔记 使用vscode外部console出现闪退-12
前言 在使用vscode的外部console时,会出现闪退现象,这是因为程序运行结束后,系统自动退出了终端(终端机制决定的)。我们可以在C程序结束后,使用system函数来暂停DOS终端系统,这样就可以完整地看…...

从Spring源码看Spring如何解决循环引用的问题
Spring如何解决循环引用的问题 关于循环引用,首先说一个结论: Spring能够解决的情况为:两个对象都是单实例、且通过set方法进行注入。 两个对象都是单实例,通过构造方法进行注入,Spring不能进行循环引用问题&#x…...
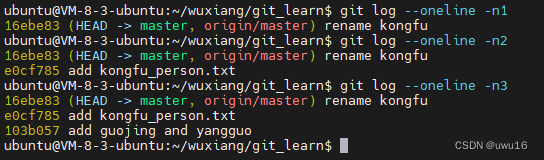
03 - 通过git log可以查看版本演变历史
通过git log可以查看版本演变历史 主要包括: commit 哈希id提交的Author信息提交的日期和时间commit info信息 git log本人常用,显示简洁: git log --oneline当log条数很多的时候,可以如下指定显示的数量: git log…...

【图论】单源最短路
算法提高课笔记。(本篇还未更新完… 目录 单源最短路的建图方式例题热浪题意思路代码 信使题意思路代码 香甜的黄油题意思路代码 最小花费题意思路代码 最优乘车题意思路代码 昂贵的聘礼题意思路代码 单源最短路的建图方式 最短路问题可以分为以下两类:…...

简易版抽奖活动的设计技术方案
1.前言 本技术方案旨在设计一套完整且可靠的抽奖活动逻辑,确保抽奖活动能够公平、公正、公开地进行,同时满足高并发访问、数据安全存储与高效处理等需求,为用户提供流畅的抽奖体验,助力业务顺利开展。本方案将涵盖抽奖活动的整体架构设计、核心流程逻辑、关键功能实现以及…...
)
rknn优化教程(二)
文章目录 1. 前述2. 三方库的封装2.1 xrepo中的库2.2 xrepo之外的库2.2.1 opencv2.2.2 rknnrt2.2.3 spdlog 3. rknn_engine库 1. 前述 OK,开始写第二篇的内容了。这篇博客主要能写一下: 如何给一些三方库按照xmake方式进行封装,供调用如何按…...

【WiFi帧结构】
文章目录 帧结构MAC头部管理帧 帧结构 Wi-Fi的帧分为三部分组成:MAC头部frame bodyFCS,其中MAC是固定格式的,frame body是可变长度。 MAC头部有frame control,duration,address1,address2,addre…...

【网络安全产品大调研系列】2. 体验漏洞扫描
前言 2023 年漏洞扫描服务市场规模预计为 3.06(十亿美元)。漏洞扫描服务市场行业预计将从 2024 年的 3.48(十亿美元)增长到 2032 年的 9.54(十亿美元)。预测期内漏洞扫描服务市场 CAGR(增长率&…...

【SQL学习笔记1】增删改查+多表连接全解析(内附SQL免费在线练习工具)
可以使用Sqliteviz这个网站免费编写sql语句,它能够让用户直接在浏览器内练习SQL的语法,不需要安装任何软件。 链接如下: sqliteviz 注意: 在转写SQL语法时,关键字之间有一个特定的顺序,这个顺序会影响到…...

Mac软件卸载指南,简单易懂!
刚和Adobe分手,它却总在Library里给你写"回忆录"?卸载的Final Cut Pro像电子幽灵般阴魂不散?总是会有残留文件,别慌!这份Mac软件卸载指南,将用最硬核的方式教你"数字分手术"࿰…...

vue3 定时器-定义全局方法 vue+ts
1.创建ts文件 路径:src/utils/timer.ts 完整代码: import { onUnmounted } from vuetype TimerCallback (...args: any[]) > voidexport function useGlobalTimer() {const timers: Map<number, NodeJS.Timeout> new Map()// 创建定时器con…...

04-初识css
一、css样式引入 1.1.内部样式 <div style"width: 100px;"></div>1.2.外部样式 1.2.1.外部样式1 <style>.aa {width: 100px;} </style> <div class"aa"></div>1.2.2.外部样式2 <!-- rel内表面引入的是style样…...

工业自动化时代的精准装配革新:迁移科技3D视觉系统如何重塑机器人定位装配
AI3D视觉的工业赋能者 迁移科技成立于2017年,作为行业领先的3D工业相机及视觉系统供应商,累计完成数亿元融资。其核心技术覆盖硬件设计、算法优化及软件集成,通过稳定、易用、高回报的AI3D视觉系统,为汽车、新能源、金属制造等行…...
Reasoning over Uncertain Text by Generative Large Language Models
https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829 1. 概述 文本中的不确定性在许多语境中传达,从日常对话到特定领域的文档(例如医学文档)(Heritage 2013;Landmark、Gulbrandsen 和 Svenevei…...
