matlab解常微分方程常用数值解法1:前向欧拉法和改进的欧拉法
总结和记录一下matlab求解常微分方程常用的数值解法,本文先从欧拉法和改进的欧拉法讲起。
d x d t = f ( x , t ) , x ( t 0 ) = x 0 \frac{d x}{d t}=f(x, t), \quad x\left(t_{0}\right)=x_{0} dtdx=f(x,t),x(t0)=x0
1. 前向欧拉法
前向欧拉法使用了泰勒展开的第一项线性项逼近。
x ( t 0 + h ) = x ( t 0 ) + h x ′ ( t 0 ) + 1 2 x ′ ′ ( ξ ) h 2 , t 0 < ξ < t 0 + h x\left(t_{0}+h\right)=x\left(t_{0}\right)+h x^{\prime}\left(t_{0}\right)+\frac{1}{2} x^{\prime \prime}(\xi) h^{2}, \quad t_{0}<\xi<t_{0}+h x(t0+h)=x(t0)+hx′(t0)+21x′′(ξ)h2,t0<ξ<t0+h
x k + 1 = x k + h x k ′ + O ( h 2 ) = x k + h f ( x k , t k ) + O ( h 2 ) x_{k+1}=x_{k}+h x'_k+O\left(h^{2}\right)=x_{k}+h f\left(x_{k}, t_{k}\right)+O\left(h^{2}\right) xk+1=xk+hxk′+O(h2)=xk+hf(xk,tk)+O(h2)
2. 改进的欧拉法
在原来前向欧拉法的基础上泰勒展开使用了前面两项:
x k + 1 = x k + h x k ′ + 1 2 h 2 x k ′ ′ + O ( h 3 ) x_{k+1}=x_{k}+h x^{\prime}_k+\frac{1}{2} h^{2} x_{k}^{\prime \prime}+O\left(h^{3}\right) xk+1=xk+hxk′+21h2xk′′+O(h3)
这里使用:
x k ′ ′ = x k + 1 ′ − x k ′ h x_{k}^{\prime \prime}=\frac{x_{k+1}^{\prime}-x_{k}^{\prime}}{h} xk′′=hxk+1′−xk′
于是我们有:
x k + 1 = x k + h 2 ( x k ′ + x k + 1 ′ ) + O ( h 3 ) x_{k+1}=x_{k}+\frac{h}{2}\left(x_{k}^{\prime}+x_{k+1}^{\prime}\right)+O\left(h^{3}\right) xk+1=xk+2h(xk′+xk+1′)+O(h3)
也就是:
x k + 1 = x k + h 2 [ f ( x k , t k ) + f ( x k + 1 , t k + 1 ) ] + O ( h 3 ) x_{k+1}=x_{k}+\frac{h}{2}\left[f\left(x_{k}, t_{k}\right)+f\left(x_{k+1}, t_{k+1}\right)\right]+O\left(h^{3}\right) xk+1=xk+2h[f(xk,tk)+f(xk+1,tk+1)]+O(h3)
我们怎么计算 f ( x k + 1 , t k + 1 ) f(x_{k+1},t_{k+1}) f(xk+1,tk+1)呢,因为我们还不知道 x k + 1 x_{k+1} xk+1。
对比前向欧拉法,改进欧拉法的右边不使用 x k + 1 x_{k+1} xk+1(我们还不知道),但是我们可以用前向欧拉法计算的 x k + h f ( x k , t k ) x_{k}+h f\left(x_{k}, t_{k}\right) xk+hf(xk,tk)来代替 x k + 1 x_{k+1} xk+1,于是我们有
x k + 1 = x k + 1 2 ( k 1 + k 2 ) + O ( h 3 ) , 其中: k 1 = h f ( x k , t k ) , k 2 = h f ( x k + h , t k + k 1 ) x_{k+1}=x_{k}+\frac{1}{2}\left(k_{1}+k_{2}\right)+O\left(h^{3}\right), \\\text{其中:}k_{1}=h f\left(x_{k}, t_{k}\right), k_{2}=h f\left(x_{k}+h, t_{k}+k_{1}\right) xk+1=xk+21(k1+k2)+O(h3),其中:k1=hf(xk,tk),k2=hf(xk+h,tk+k1)
对比一下前向欧拉法:
x k + 1 = x k + k 1 + O ( h 2 ) , k 1 = h f ( x k , t k ) x_{k+1}=x_{k}+k_{1}+O\left(h^{2}\right), \quad k_{1}=h f\left(x_{k},t_{k} \right) xk+1=xk+k1+O(h2),k1=hf(xk,tk)
例子
x ′ = x + t , x ( 0 ) = 1 x^{\prime}=x+t, \quad x(0)=1 x′=x+t,x(0)=1
clear% 测试三个不同的步长
test_times = 3;
% 保存时间、差分时间和步长
h_res=ones(1,test_times);
t_res=cell(1,test_times);%时间
tplot_res=cell(1,test_times);%差分的时间,比时间长度少1
% 保存两种数值方法和解析解的计算结果
x_euler_res=cell(1,test_times);
x_modified_res=cell(1,test_times);
x_exact_res=cell(1,test_times);
% 保存误差
diff1_res=cell(1,test_times);
diff2_res=cell(1,test_times);for i = 1:test_times
% 设置步长间隔和步长数
h = 1/10^i; n = 10/h;
% set up initial conditions
t=zeros(n+1,1); t(1) = 0;
x_euler=zeros(n+1,1); x_euler(1) = 1;
x_modified=zeros(n+1,1); x_modified(1) = 1;
x_exact=zeros(n+1,1); x_exact(1) = 1;
% 设置不同的比较误差的图
diff1 = zeros(n,1); diff2 = zeros(n,1); tplot = zeros(n,1);
% define right side of differential equation, Equation 1.7.10
f = inline('xx+tt','tt','xx');
for k = 1:n
t(k+1) = t(k) + h;
% 计算解析解
x_exact(k+1) = 2*exp(t(k+1)) - t(k+1) - 1;
% 使用前向欧拉法计算
k1 = h * f(t(k),x_euler(k));
x_euler(k+1) = x_euler(k) + k1;
tplot(k) = t(k+1);
diff1(k) = x_euler(k+1) - x_exact(k+1);
diff1(k) = abs(diff1(k) / x_exact(k+1));
% 使用改进欧拉法计算
k1 = h * f(t(k),x_modified(k));
k2 = h * f(t(k+1),x_modified(k)+k1);
x_modified(k+1) = x_modified(k) + 0.5*(k1+k2);
diff2(k) = x_modified(k+1) - x_exact(k+1);
diff2(k) = abs(diff2(k) / x_exact(k+1));
end
diff1_res{i}=diff1;
diff2_res{i}=diff2;
tplot_res{i}=tplot;
h_res(i)=h;
x_euler_res{i}=x_euler;
x_modified_res{i}=x_modified;
x_exact_res{i}=x_exact;
t_res{i}=t;
endfigure
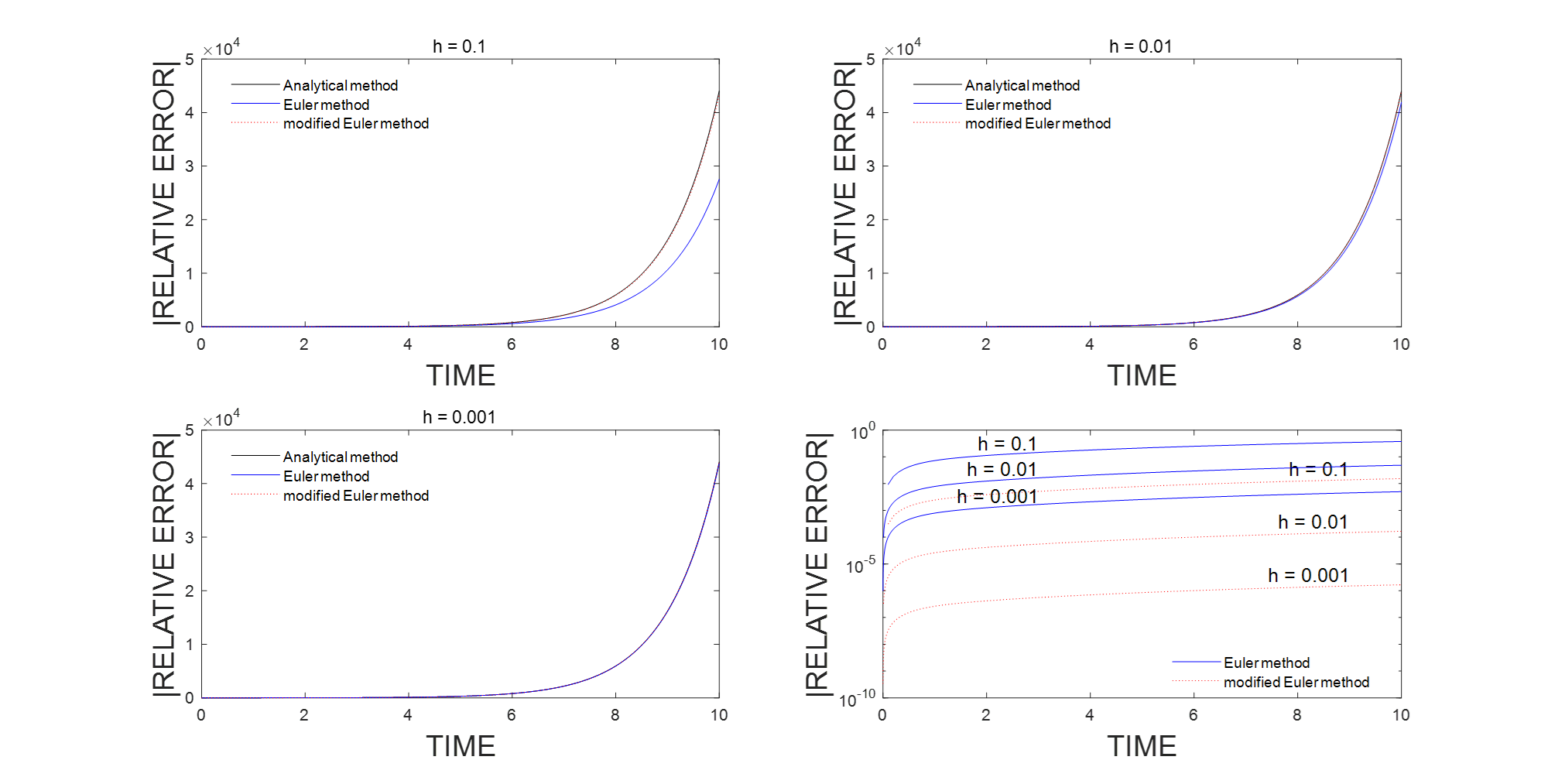
for i=1:test_times
subplot(2,2,i)
plot(t_res{i},x_exact_res{i},'k-',t_res{i},x_euler_res{i},'b-',t_res{i},x_modified_res{i},'r:')
xlabel('TIME','Fontsize',18)
ylabel('|RELATIVE ERROR|','Fontsize',18)
legend({'Analytical method','Euler method','modified Euler method'},'Location','best')
legend boxoff;
title(['h = ',num2str(h_res(i))]);
end
subplot(2,2,4)% 计算相对误差
for i=1:test_times
semilogy(tplot_res{i},diff1_res{i},'b-',tplot_res{i},diff2_res{i},'r:')
hold on
num1 = 0.2*10/h_res(i); num2 = 0.8*10/h_res(i);
text(3,diff1_res{i}(num1),['h = ',num2str(h_res(i))],'Fontsize',12,...
'HorizontalAlignment','right',...
'VerticalAlignment','bottom')
text(9,diff2_res{i}(num2),['h = ',num2str(h_res(i))],'Fontsize',12,...
'HorizontalAlignment','right',...
'VerticalAlignment','bottom')
end
xlabel('TIME','Fontsize',18)
ylabel('|RELATIVE ERROR|','Fontsize',18)
legend({'Euler method','modified Euler method'},'Location','best')
legend boxoff;我们对各个不同的步长进行了比较,并比较了它们的误差,发现改进的欧拉法要比前向欧拉法的精度更高。随着步长的变小,误差也在变小。
相关文章:

matlab解常微分方程常用数值解法1:前向欧拉法和改进的欧拉法
总结和记录一下matlab求解常微分方程常用的数值解法,本文先从欧拉法和改进的欧拉法讲起。 d x d t f ( x , t ) , x ( t 0 ) x 0 \frac{d x}{d t}f(x, t), \quad x\left(t_{0}\right)x_{0} dtdxf(x,t),x(t0)x0 1. 前向欧拉法 前向欧拉法使用了泰勒展开的第…...
SQL | 计算字段
7-创建计算字段 7.1-计算字段 存储在数据库中的数据一般不是我们所需要的字段格式, 需要公司名称,同时也需要公司地址,但是这两个数据存储在不同的列中。 省,市,县和邮政编码存储在不同的列中,但是当我们…...

leetcode做题笔记67
给你两个二进制字符串 a 和 b ,以二进制字符串的形式返回它们的和。 思路一:模拟题意 void reserve(char* s) {int len strlen(s);for (int i 0; i < len / 2; i) {char t s[i];s[i] s[len - i - 1], s[len - i - 1] t;} }char* addBinary(cha…...
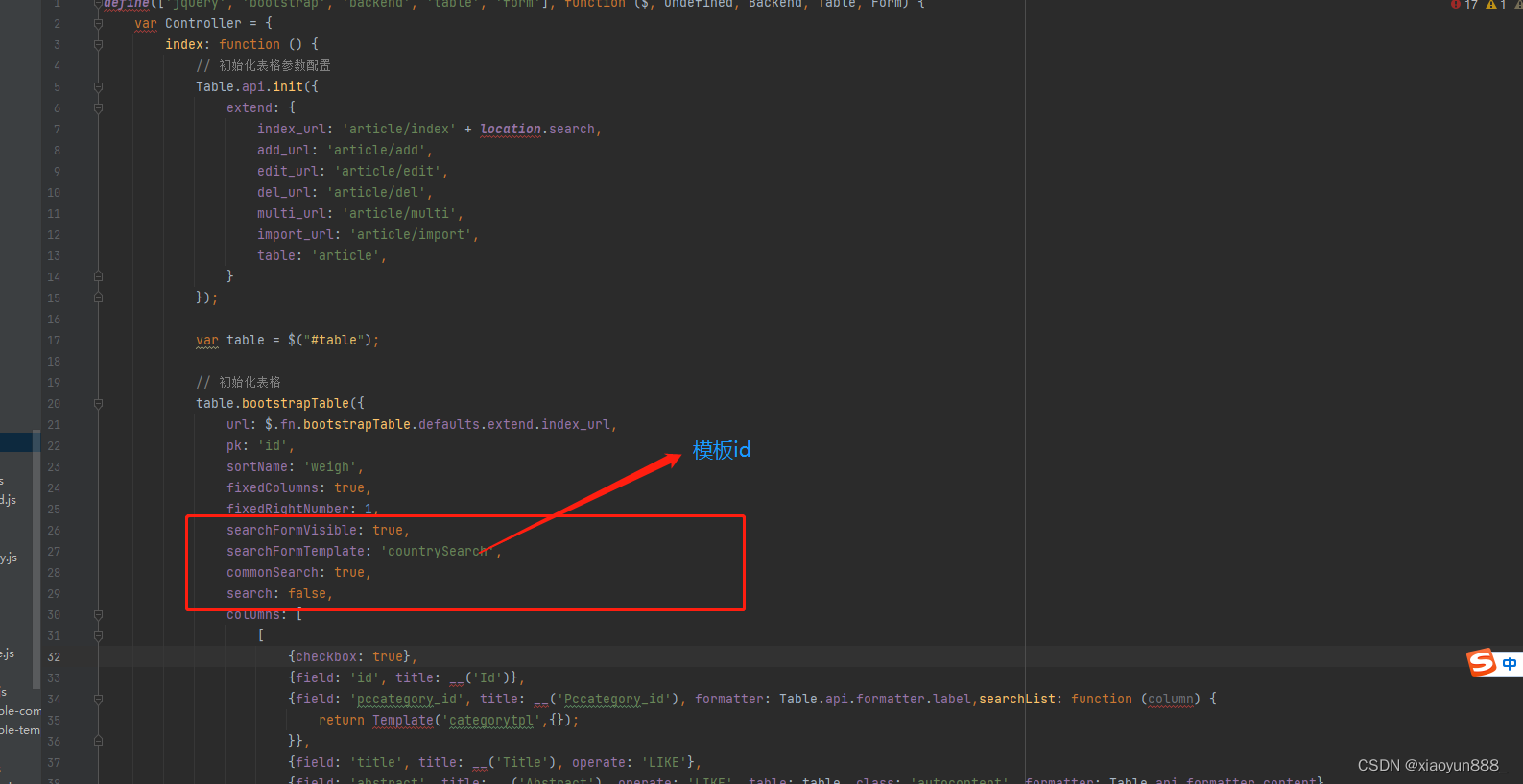
fastadmin 自定义搜索分类和时间范围
1.分类搜索,分类信息获取----php 2.对应html页面,页面底部加搜索提交代码(这里需要注意:红框内容) 图上代码----方便直接复制使用 <script id"countrySearch" type"text/html"><!--form…...

Oracle Data Redaction与Data Pump
如果表定义了Redaction Policy,导出时数据会脱敏吗?本文解答这个问题。 按照Oracle文档Advanced Security Guide第13章,13.6.5的Tutorial,假设表HR.jobs定义了Redaction Policy。 假设HR用户被授予了访问目录对象的权限…...

设计模式(6)原型模式
一、介绍 Java中自带的原型模式是clone()方法。该方法是Object的方法,native类型。他的作用就是将对象的在内存的那一块内存数据一字不差地再复制一个。我们写简单类的时候只需要实现Cloneable接口,然后调用Object::clone方法就可实现克隆功能。这样实现…...

pywinauto结合selenium实现文件上传
简介 PC端-Windows上的元素识别可用viewWizard工具 PC端-Windows上的元素操作可用pywinauto库 浏览器上网页的元素识别可用selenium 安装 pip installer pywinauto 使用须知 pywinauto官方文档 确定app的可访问技术 1、win32 API(backend=“win32”) 一般是MFC、VB6、VC…...
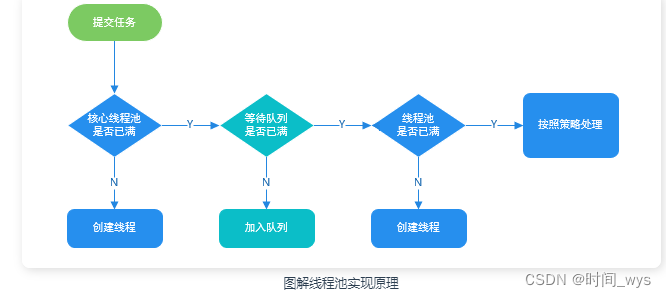
【Java多线程学习7】Java线程池技术
线程池技术 一、什么是线程池 线程池顾名思义是管理一组线程的池子。当有任务要处理时,直接从线程池中获取线程来处理,处理完之后线程不会立即销毁,而是等待下一个任务。 二、为什么要使用线程池? 线程池的作用? 1、降低资源…...
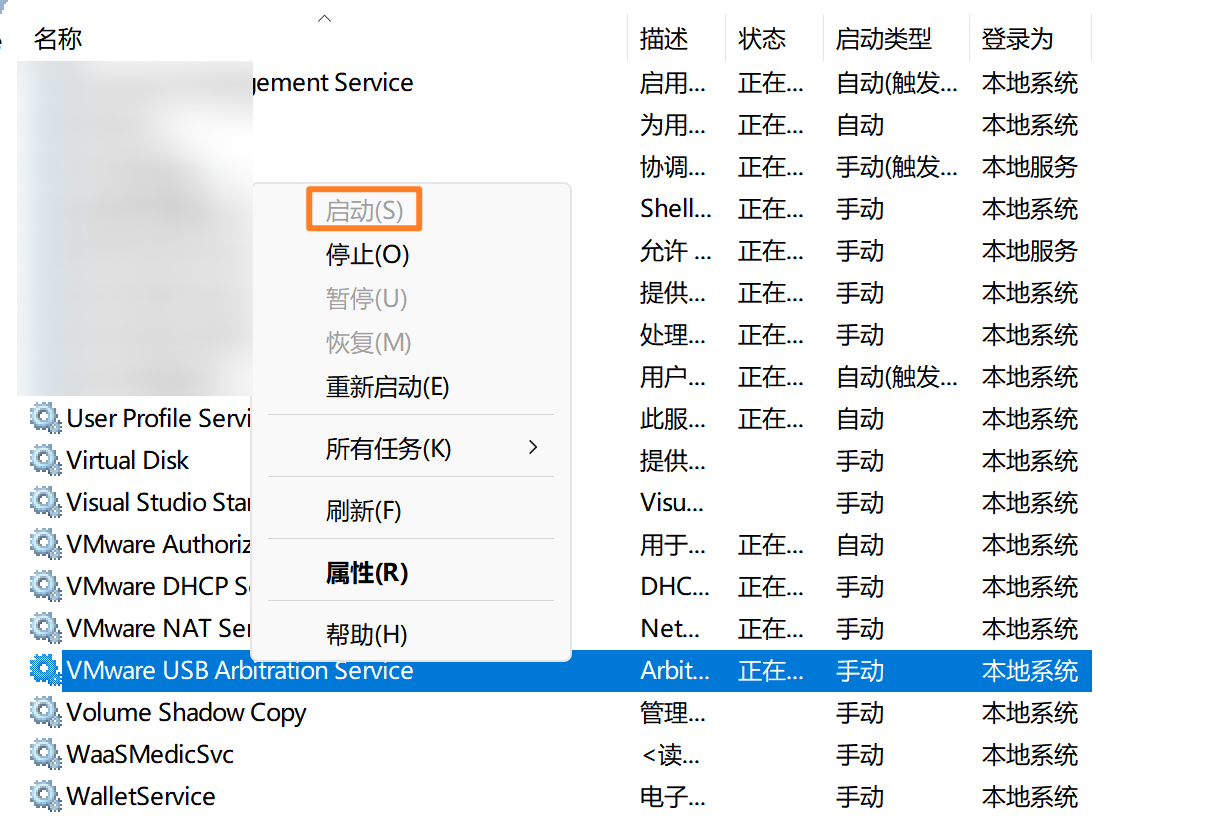
VMware虚拟机NAT模式Ubuntu无法上网解决方案
发现只要NAT模式,ping地址时就报网络不可达,且右上方网络图标消失,但是外部USB网络设备又只能在NAT模式下使用。。。 博主的解决方案如下: 按WinR键入services.msc, 找到VMware DHCP Service、VMware NAT Service和V…...

Linux中无法忘记mysql密码处理办法
找到/etc/my.cnf或者/etc/mysql/my.cnf文件 添加下面两行代码,取消密码验证 [mysqld] skip-grant-table使用命令登录:mysql -u root -p,回车,回车使用sql语句来修改密码 mysql>use mysql; mysql>update user set password…...
)
vue 使用 el-upload 上传文件(自动上传/手动上传)
vue 使用 el-upload 上传文件(自动上传/手动上传) 文章目录 1. 自动上传(选择完文件后,调用axios上传)2.手动上传 1. 自动上传(选择完文件后,调用axios上传) <el-uploadref"upload1"action:multiple"false"accept".xlsx,.csv,.xls":auto-upl…...
服务器遭受攻击之后的常见思路
哈喽大家好,我是咸鱼 不知道大家有没有看过这么一部电影: 这部电影讲述了男主是一个电脑极客,在计算机方面有着不可思议的天赋,男主所在的黑客组织凭借着超高的黑客技术去入侵各种国家机构的系统,并引起了德国秘密警察…...
C语言学习笔记 使用vscode外部console出现闪退-12
前言 在使用vscode的外部console时,会出现闪退现象,这是因为程序运行结束后,系统自动退出了终端(终端机制决定的)。我们可以在C程序结束后,使用system函数来暂停DOS终端系统,这样就可以完整地看…...

从Spring源码看Spring如何解决循环引用的问题
Spring如何解决循环引用的问题 关于循环引用,首先说一个结论: Spring能够解决的情况为:两个对象都是单实例、且通过set方法进行注入。 两个对象都是单实例,通过构造方法进行注入,Spring不能进行循环引用问题&#x…...
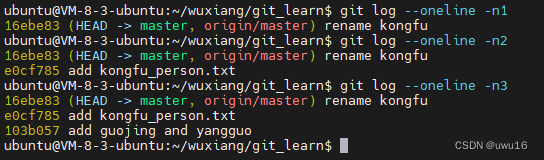
03 - 通过git log可以查看版本演变历史
通过git log可以查看版本演变历史 主要包括: commit 哈希id提交的Author信息提交的日期和时间commit info信息 git log本人常用,显示简洁: git log --oneline当log条数很多的时候,可以如下指定显示的数量: git log…...

【图论】单源最短路
算法提高课笔记。(本篇还未更新完… 目录 单源最短路的建图方式例题热浪题意思路代码 信使题意思路代码 香甜的黄油题意思路代码 最小花费题意思路代码 最优乘车题意思路代码 昂贵的聘礼题意思路代码 单源最短路的建图方式 最短路问题可以分为以下两类:…...

闻道网络:2023宠物消费网络营销洞察数据报告(附下载)
关于报告的所有内容,公众【营销人星球】获取下载查看 核心观点 行业持续升级,增速放缓,正朝着多元化和专业化的方向发展;自公共事件以来,因,“猫不用遛”,养猫人士增速迅猛反超犬主人…...
Docker 安装和架构说明
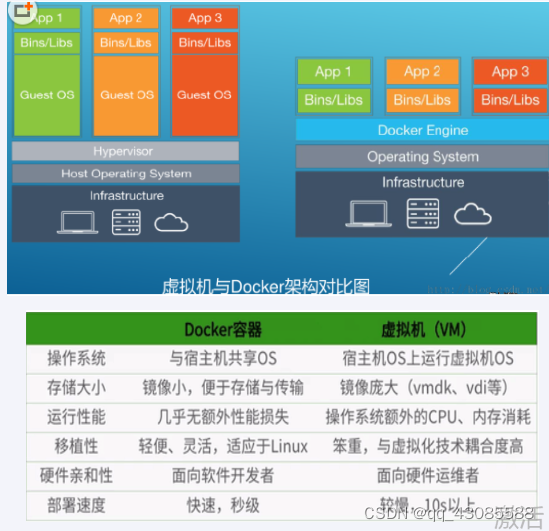
Docker 并非是一个通用的容器工具,它依赖于已存在并运行的Linux内核环境。 Docker实质上是在已经运行的Liunx下制造了一个隔离的文件环境,因此他的执行效率几乎等同于所部署的linux主机。因此Docker必须部署在Linux内核系统上。如果其他系统想部署Docke…...
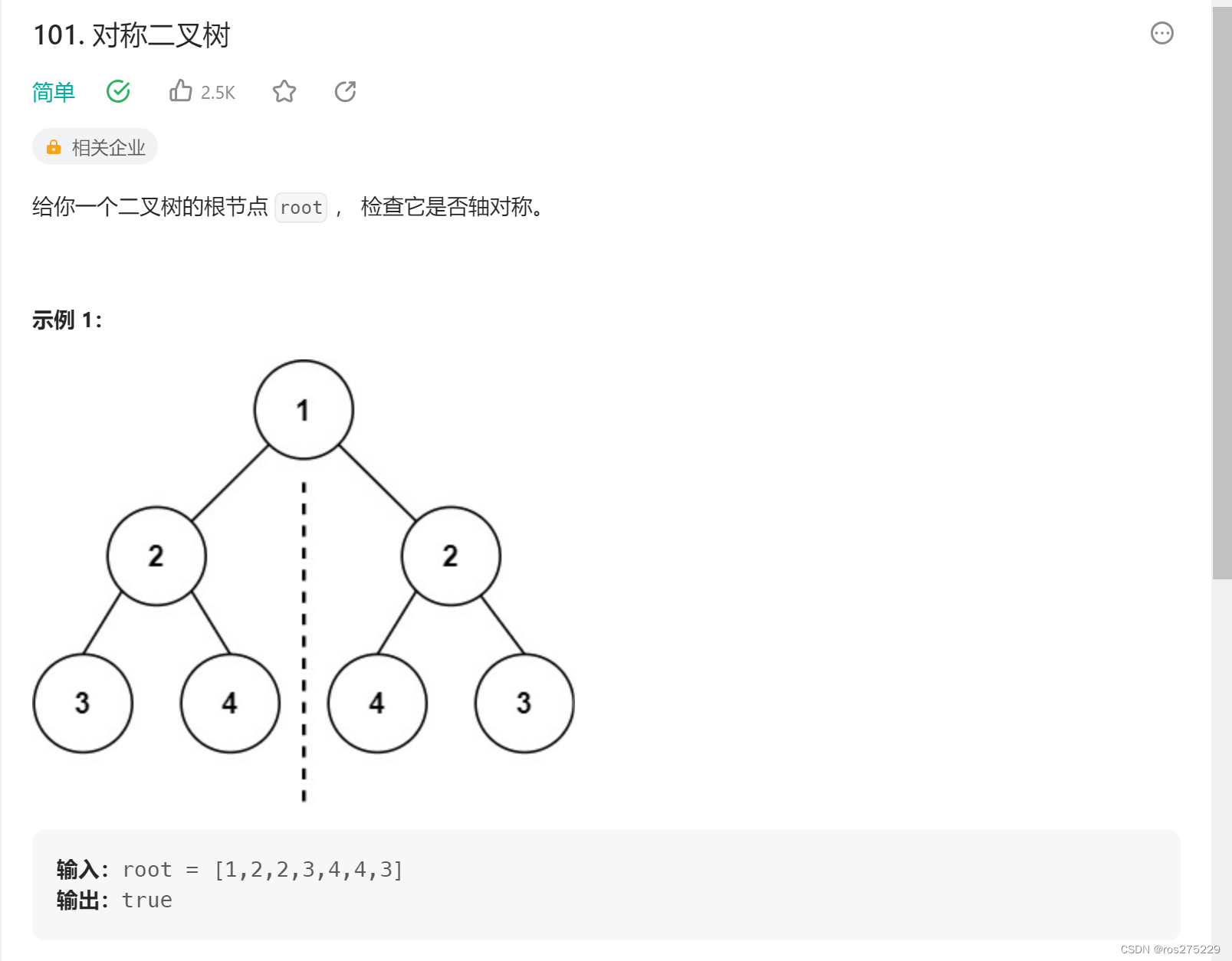
101. 对称二叉树
题目 原题链接 : 101.对称二叉树 题面 : 对于这一题呢,题目要求给出递归和迭代两种方式来解决!!! 注 : 这一题不仅仅是判断左右两个子节点是否对称,而是要遍历两棵树而且要比较内侧和外侧节点 递归 先确认递归三要素 : 确定递归函数的参数和返回值 bool …...

cmake应用:集成gtest进行单元测试
编写代码有bug是很正常的,通过编写完备的单元测试,可以及时发现问题,并且在后续的代码改进中持续观测是否引入了新的bug。对于追求质量的程序员,为自己的代码编写全面的单元测试是必备的基础技能,在编写单元测试的时候…...
结构体的进阶应用)
基于算法竞赛的c++编程(28)结构体的进阶应用
结构体的嵌套与复杂数据组织 在C中,结构体可以嵌套使用,形成更复杂的数据结构。例如,可以通过嵌套结构体描述多层级数据关系: struct Address {string city;string street;int zipCode; };struct Employee {string name;int id;…...

Lombok 的 @Data 注解失效,未生成 getter/setter 方法引发的HTTP 406 错误
HTTP 状态码 406 (Not Acceptable) 和 500 (Internal Server Error) 是两类完全不同的错误,它们的含义、原因和解决方法都有显著区别。以下是详细对比: 1. HTTP 406 (Not Acceptable) 含义: 客户端请求的内容类型与服务器支持的内容类型不匹…...

Admin.Net中的消息通信SignalR解释
定义集线器接口 IOnlineUserHub public interface IOnlineUserHub {/// 在线用户列表Task OnlineUserList(OnlineUserList context);/// 强制下线Task ForceOffline(object context);/// 发布站内消息Task PublicNotice(SysNotice context);/// 接收消息Task ReceiveMessage(…...

8k长序列建模,蛋白质语言模型Prot42仅利用目标蛋白序列即可生成高亲和力结合剂
蛋白质结合剂(如抗体、抑制肽)在疾病诊断、成像分析及靶向药物递送等关键场景中发挥着不可替代的作用。传统上,高特异性蛋白质结合剂的开发高度依赖噬菌体展示、定向进化等实验技术,但这类方法普遍面临资源消耗巨大、研发周期冗长…...

iPhone密码忘记了办?iPhoneUnlocker,iPhone解锁工具Aiseesoft iPhone Unlocker 高级注册版分享
平时用 iPhone 的时候,难免会碰到解锁的麻烦事。比如密码忘了、人脸识别 / 指纹识别突然不灵,或者买了二手 iPhone 却被原来的 iCloud 账号锁住,这时候就需要靠谱的解锁工具来帮忙了。Aiseesoft iPhone Unlocker 就是专门解决这些问题的软件&…...

为什么需要建设工程项目管理?工程项目管理有哪些亮点功能?
在建筑行业,项目管理的重要性不言而喻。随着工程规模的扩大、技术复杂度的提升,传统的管理模式已经难以满足现代工程的需求。过去,许多企业依赖手工记录、口头沟通和分散的信息管理,导致效率低下、成本失控、风险频发。例如&#…...

【Zephyr 系列 10】实战项目:打造一个蓝牙传感器终端 + 网关系统(完整架构与全栈实现)
🧠关键词:Zephyr、BLE、终端、网关、广播、连接、传感器、数据采集、低功耗、系统集成 📌目标读者:希望基于 Zephyr 构建 BLE 系统架构、实现终端与网关协作、具备产品交付能力的开发者 📊篇幅字数:约 5200 字 ✨ 项目总览 在物联网实际项目中,**“终端 + 网关”**是…...

OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别
OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别 直接训练提示词嵌入向量的核心区别 您提到的代码: prompt_embedding = initial_embedding.clone().requires_grad_(True) optimizer = torch.optim.Adam([prompt_embedding...

html-<abbr> 缩写或首字母缩略词
定义与作用 <abbr> 标签用于表示缩写或首字母缩略词,它可以帮助用户更好地理解缩写的含义,尤其是对于那些不熟悉该缩写的用户。 title 属性的内容提供了缩写的详细说明。当用户将鼠标悬停在缩写上时,会显示一个提示框。 示例&#x…...

JVM虚拟机:内存结构、垃圾回收、性能优化
1、JVM虚拟机的简介 Java 虚拟机(Java Virtual Machine 简称:JVM)是运行所有 Java 程序的抽象计算机,是 Java 语言的运行环境,实现了 Java 程序的跨平台特性。JVM 屏蔽了与具体操作系统平台相关的信息,使得 Java 程序只需生成在 JVM 上运行的目标代码(字节码),就可以…...
