101. 对称二叉树
题目
原题链接 : 101.对称二叉树
题面 :
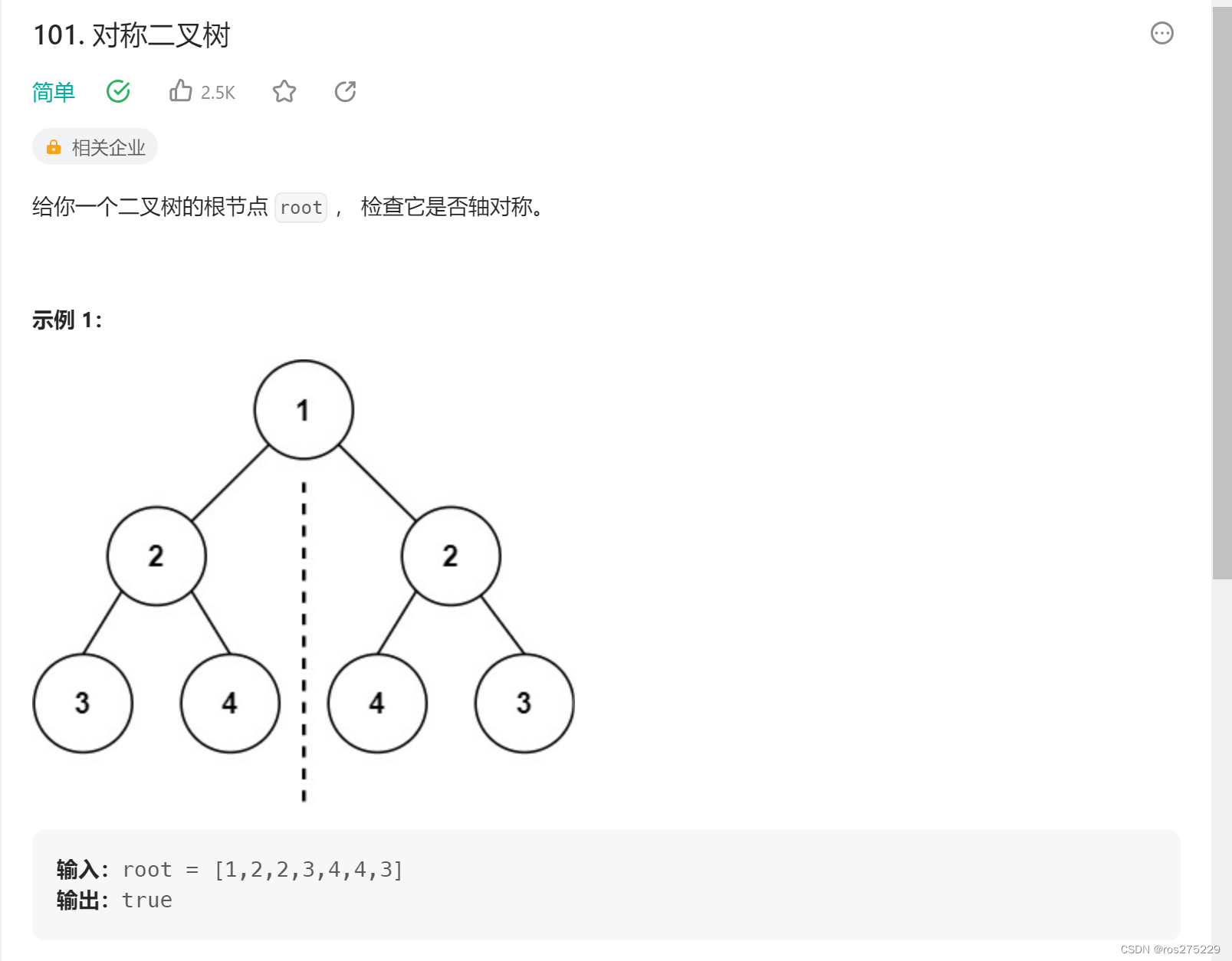
对于这一题呢,题目要求给出递归和迭代两种方式来解决!!!
注 :
- 这一题不仅仅是判断左右两个子节点是否对称,而是要遍历两棵树而且要比较内侧和外侧节点
递归
先确认递归三要素 :
- 确定递归函数的参数和返回值
bool cmp(TreeNode* left,TreeNode* right){}- 确认终止条件
- 左节点和右结点一个非空,那么一定不对称,返回false;
- 左右结点均为空,那么对称,返回true
- 均不为空,值不相等,返回false,值相等,返回下一步,即继续向下递归
那么递归函数的整体代码也就写好了 :
bool cmp(TreeNode* left,TreeNode* right){if(left==nullptr && right!=nullptr) return false;else if(left!=nullptr && right==nullptr) return false;else if(left==nullptr && right==nullptr) return true;else if(left->val != right->val) return false;else return cmp(left->left,right->right) && cmp(left->right,right->left);}- 确认递归的逻辑 :
bool outside = cmp(left->left, right->right); // 左子树:左、 右子树:右
bool inside = cmp(left->right, right->left); // 左子树:右、 右子树:左
bool isSame = outside && inside; // 左子树:中、 右子树:中(逻辑处理)
return isSame;那么题解代码也就出来了 :
/*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* TreeNode() : val(0), left(nullptr), right(nullptr) {}* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:bool cmp(TreeNode* left,TreeNode* right){if(left==nullptr && right!=nullptr) return false;else if(left!=nullptr && right==nullptr) return false;else if(left==nullptr && right==nullptr) return true;else if(left->val != right->val) return false;else return cmp(left->left,right->right) && cmp(left->right,right->left);}bool isSymmetric(TreeNode* root) {if(root == nullptr) return true;return cmp(root->left,root->right);}
};
迭代
迭代的思路和想法与递归相同,这里呢,就用queue队列来模拟
详细请看代码 :
/*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* TreeNode() : val(0), left(nullptr), right(nullptr) {}* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:bool isSymmetric(TreeNode* root) {if(root == nullptr) return true;queue<TreeNode*> que;que.push(root->left);que.push(root->right);while(!que.empty()){TreeNode* l = que.front();que.pop();TreeNode* r = que.front();que.pop();if(!l && !r) continue;//左右结点均为空,直接下一步;if((l&&!r) || (!l&&r)) return false;//左右结点一个为空,返回false;if(l->val != r->val) return false;//均不为空但不相等,直接返回false;que.push(l->left);que.push(r->right);que.push(l->right);que.push(r->left);}return true;}
};最后看完,能给个赞吗,hh!!!
相关文章:

101. 对称二叉树
题目 原题链接 : 101.对称二叉树 题面 : 对于这一题呢,题目要求给出递归和迭代两种方式来解决!!! 注 : 这一题不仅仅是判断左右两个子节点是否对称,而是要遍历两棵树而且要比较内侧和外侧节点 递归 先确认递归三要素 : 确定递归函数的参数和返回值 bool …...

cmake应用:集成gtest进行单元测试
编写代码有bug是很正常的,通过编写完备的单元测试,可以及时发现问题,并且在后续的代码改进中持续观测是否引入了新的bug。对于追求质量的程序员,为自己的代码编写全面的单元测试是必备的基础技能,在编写单元测试的时候…...
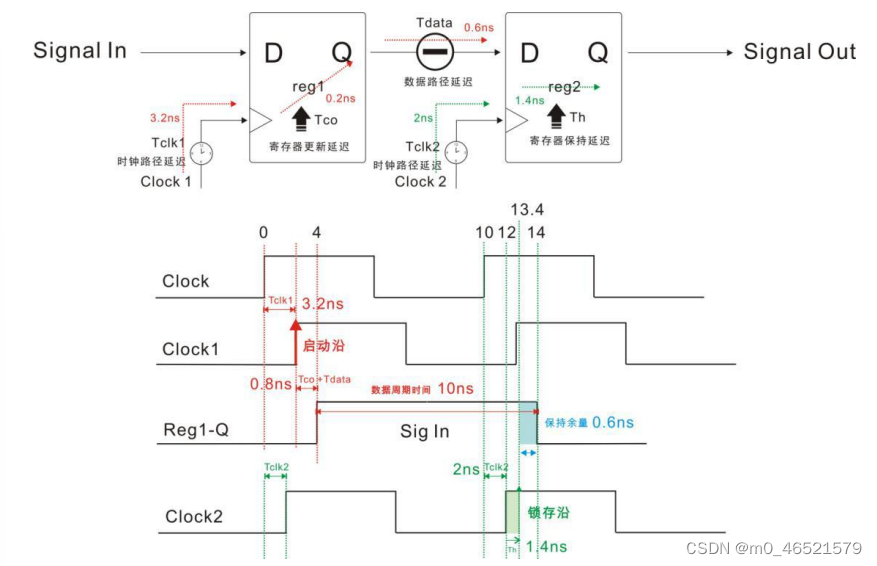
静态时序分析与时序约束
一、时序分析的基本概念 1. 时钟 理性的时钟模型是一个占空比为50%且周期固定的方波: 实际电路中输入给FPGA的晶振时钟信号是正弦波: 2. 时钟抖动 Clock Jitter,时钟抖动,相对于理想时钟沿,实际时钟存在不随时钟存在…...

YOLOv5基础知识入门(3)— 目标检测相关知识点
前言:Hello大家好,我是小哥谈。YOLO算法发展历程和YOLOv5核心基础知识学习完成之后,接下来我们就需要学习目标检测相关知识了。为了让大家后面可以顺利地用YOLOv5进行目标检测实战,本节课就带领大家学习一下目标检测的基础知识点&…...
10个AI绘图生成器让绘画更简单
AI不仅影响商业和医疗保健等行业,还在创意产业中发挥着越来越大的作用,开创了AI绘画生成器新时代。在绘画领域当然也是如此,与传统的绘画工具不同,AI人工智能时代的绘画工具是全自动的、智能的,甚至可以说是“傻瓜式”…...

干货满满的Python知识,学会这些你也能成为大牛
目录 1. 爬取网站数据 2. 数据清洗与处理 3. 数据可视化 4. 机器学习模型训练 5. 深度学习模型训练 6. 总结 1. 爬取网站数据 在我们的Python中呢,使用爬虫可以轻松地获取网站的数据。可以使用urllib、requests、BeautifulSoup等库进行数据爬取和处理。以下是…...

【Leetcode】155. 最小栈、JZ31 栈的压入、弹出序列
作者:小卢 专栏:《Leetcode》 喜欢的话:世间因为少年的挺身而出,而更加瑰丽。 ——《人民日报》 155. 最小栈 155. 最小栈 题目描述; 设计一个支持 push ,pop ,top …...
网络安全(黑客技术)自学笔记
一、什么是网络安全?什么是黑客? 网络安全可以基于攻击和防御视角来分类,我们经常听到的 “红队”、“渗透测试” 等就是研究攻击技术,而“蓝队”、“安全运营”、“安全运维”则研究防御技术。 无论网络、Web、移动、桌面、云等…...

iOS学习—制作全局遮罩
在.h文件中线声明show()方法 - (void)show; .m文件中添加全屏遮罩,在遮罩上添加了一个选择框并添加了底部弹出的动画,可自行在其中添加tableview、pickerview等其他视图,并添加了点击选择框视图外区域隐藏 #import "MaskView.h"…...

GRPC-连接池-GPT
gRPC Dart 管理优化 User grpc for dart 如何统一管理多个Client的创建和销毁,给我一个最优解 ChatGPT 对于在Dart中使用gRPC创建和销毁多个Client的统一管理,您可以使用一个单例模式的管理类来实现最优解。 首先,创建一个管理类,…...
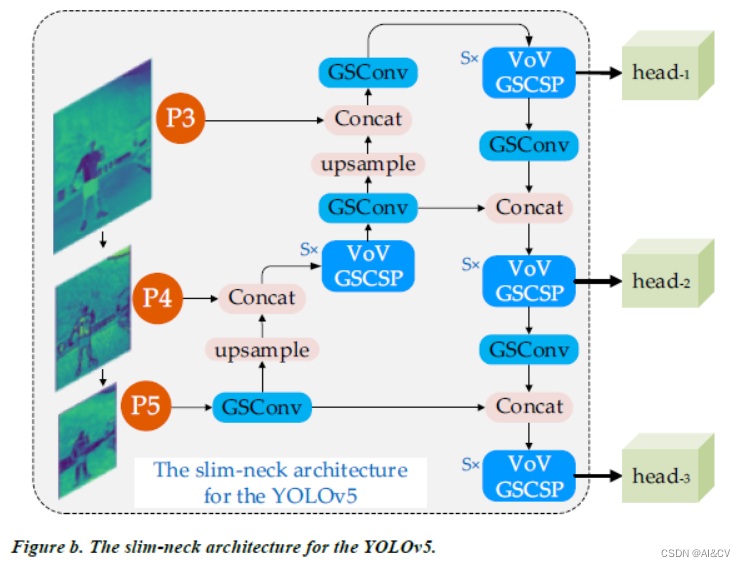
YOLOv5、YOLOv8改进: GSConv+Slim Neck
论文题目:Slim-neck by GSConv: A better design paradigm of detector architectures for autonomous vehicles 论文:https://arxiv.org/abs/2206.02424 代码:https://github.com/AlanLi1997/Slim-neck-by-GSConv 在计算机视觉领域&#x…...

重发布选路问题
一、思路 ; 1.增加不优选路开销解决选路不佳问题 2.用增加开销的方式使R1 不将ASBR传的R7传给另一台ASBR解决R1、R2、R3、R4pingR7环回环路 二、操作 ------IP地址配置如图 1.ospf及rip的宣告 rip: [r1]rip 1 [r1-rip-1]version 2 [r1-rip-1]netw…...

LinearAlgebraMIT_9_LinearIndependence/SpanningASpace/Basis/Dimension
这节课我们主要学习一下(Linear Independence)线性无关,(spanning a space)生成空间,(basis)基和(dimension)维度。同时我们要注意这四个很重要的基本概念的描述对象,我们会说向量组线性无关,由一个向量组生成的空间,子…...

Redission 解锁异常:attempt to unlock lock, not locked by current thread by node id
标题:解锁异常:Redission中的"attempt to unlock lock, not locked by current thread by node id"问题分析与解决方案 在分布式系统中,锁是常用的同步机制,用于保护共享资源,避免并发冲突。Redission是一个…...

AIGC技术揭秘:探索火热背后的原因与案例
文章目录 什么是AIGC技术?为何AIGC技术如此火热?1. 提高效率与创造力的完美结合2. 拓展应用领域,创造商业价值3. 推动技术创新和发展 AIGC技术案例解析1. 艺术创作:生成独特的艺术作品2. 内容创作:实时生成各类内容3. …...

【Linux】总结1-命令工具
文章目录 基础指令shell命令以及运行原理Linux权限粘滞位工具 基础指令 ls、pwd、touch、mkdir、netstat、cp、mv、cd、tar、zip、unzip、grep、pstack、ps、rm、cat、more、less、head、tail、find、ulimit -a、clear、whoami、man touch:创建文件,也包…...

Git远程仓库
Git远程仓库 推送拉取git fetchgit pull 克隆 推送 Git是分布式版本控制系统,同一个Git仓库,可以分布到不同的机器上。那要怎么实现这种分布呢?我们可以找一台电脑充当服务器,也就是扮演远程仓库的角色,一直都处于开机…...
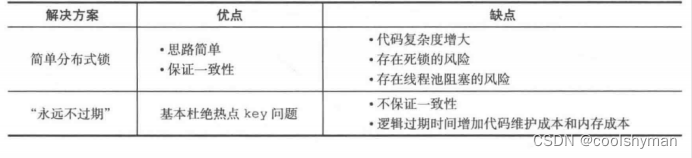
Redis缓存设计
缓存能够有效地加速应用的读写速度,同时也可以降低后端负载,对日常应用的开发至关重要。但是将缓存加入应用架构后也会带来一些问题,本文将针对这些问题介绍缓存使用技巧和设计方案。 1缓存的收益和成本 下图左侧为客户端直接调用存储层的架…...
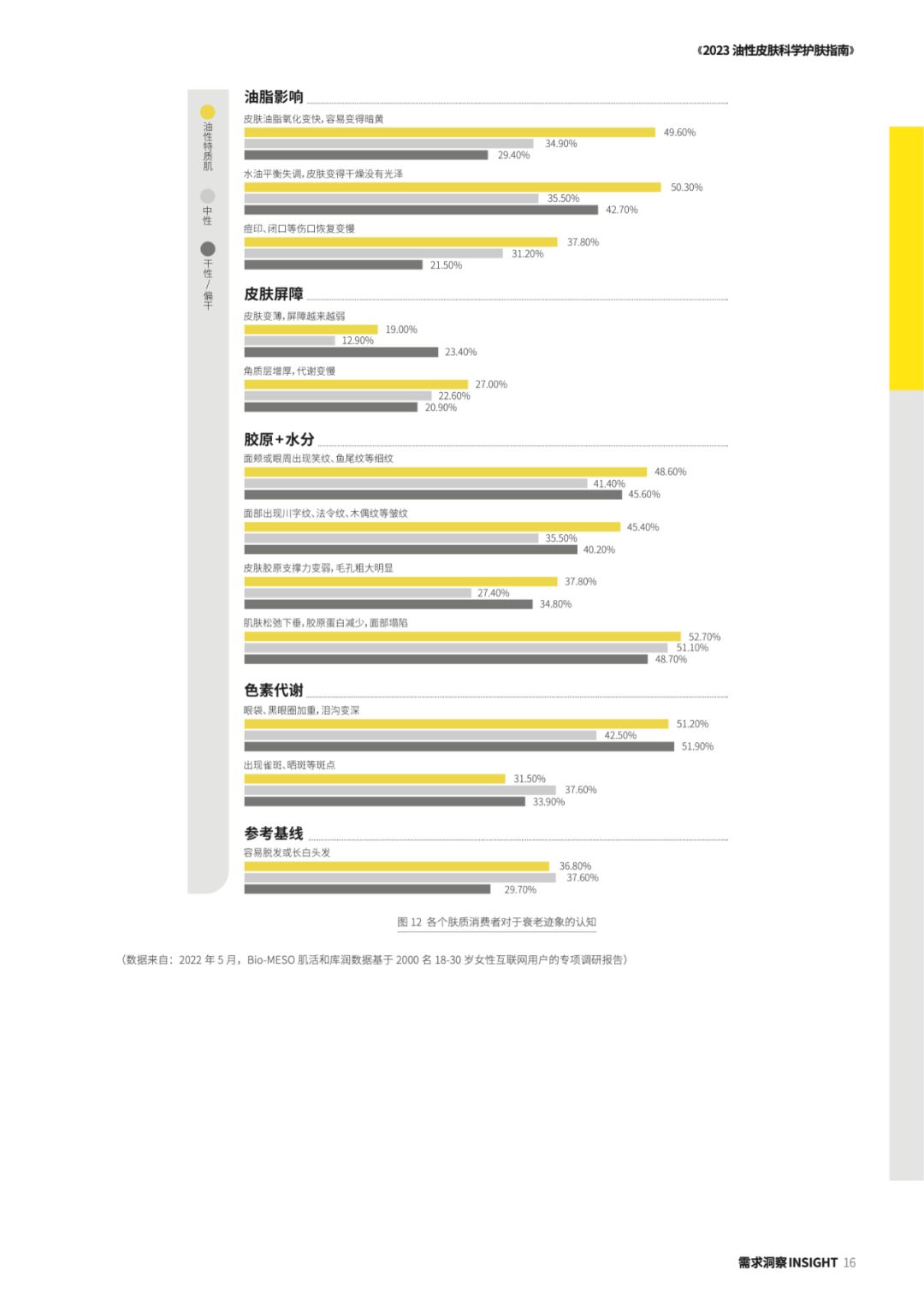
华熙生物肌活:2023年版Bio-MESO肌活油性皮肤科学护肤指南
关于报告的所有内容,公众【营销人星球】获取下载查看 核心观点 以悦己和尝鲜为消费动机的他们,已迅速崛起成为护肤行业的焦点人群。而在新生代护肤议题中,“油性皮肤护理”已经成为一个至关重要的子集。今天,中国新生代人口数量…...
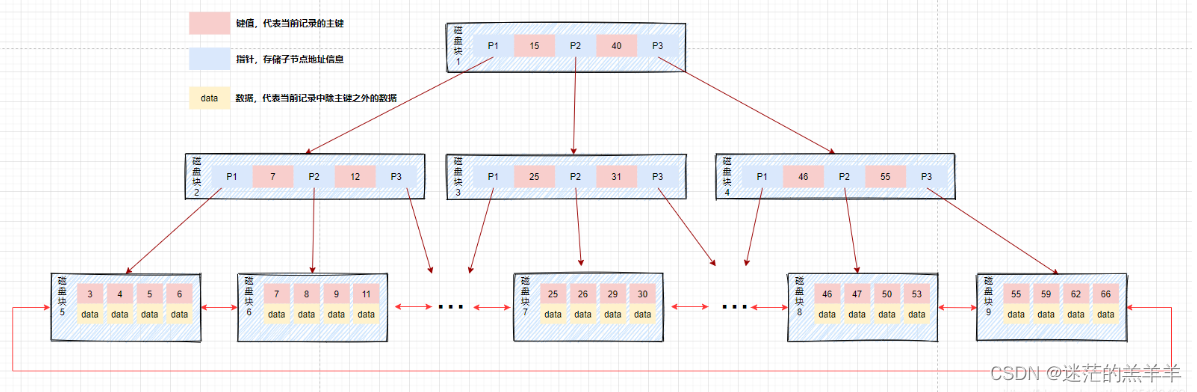
mysql索引介绍
索引可以提升查询速度,会影响where查询,以及order by排序。MySQL索引类型如下: 从索引存储结构划分:B Tree索引、Hash索引、全文索引 从应用层次划分:主键索引、唯一索引、单值索引、复合索引 从索引键值类型划分&am…...

生成xcframework
打包 XCFramework 的方法 XCFramework 是苹果推出的一种多平台二进制分发格式,可以包含多个架构和平台的代码。打包 XCFramework 通常用于分发库或框架。 使用 Xcode 命令行工具打包 通过 xcodebuild 命令可以打包 XCFramework。确保项目已经配置好需要支持的平台…...

TDengine 快速体验(Docker 镜像方式)
简介 TDengine 可以通过安装包、Docker 镜像 及云服务快速体验 TDengine 的功能,本节首先介绍如何通过 Docker 快速体验 TDengine,然后介绍如何在 Docker 环境下体验 TDengine 的写入和查询功能。如果你不熟悉 Docker,请使用 安装包的方式快…...
)
进程地址空间(比特课总结)
一、进程地址空间 1. 环境变量 1 )⽤户级环境变量与系统级环境变量 全局属性:环境变量具有全局属性,会被⼦进程继承。例如当bash启动⼦进程时,环 境变量会⾃动传递给⼦进程。 本地变量限制:本地变量只在当前进程(ba…...

React hook之useRef
React useRef 详解 useRef 是 React 提供的一个 Hook,用于在函数组件中创建可变的引用对象。它在 React 开发中有多种重要用途,下面我将全面详细地介绍它的特性和用法。 基本概念 1. 创建 ref const refContainer useRef(initialValue);initialValu…...

k8s业务程序联调工具-KtConnect
概述 原理 工具作用是建立了一个从本地到集群的单向VPN,根据VPN原理,打通两个内网必然需要借助一个公共中继节点,ktconnect工具巧妙的利用k8s原生的portforward能力,简化了建立连接的过程,apiserver间接起到了中继节…...

爬虫基础学习day2
# 爬虫设计领域 工商:企查查、天眼查短视频:抖音、快手、西瓜 ---> 飞瓜电商:京东、淘宝、聚美优品、亚马逊 ---> 分析店铺经营决策标题、排名航空:抓取所有航空公司价格 ---> 去哪儿自媒体:采集自媒体数据进…...

Java + Spring Boot + Mybatis 实现批量插入
在 Java 中使用 Spring Boot 和 MyBatis 实现批量插入可以通过以下步骤完成。这里提供两种常用方法:使用 MyBatis 的 <foreach> 标签和批处理模式(ExecutorType.BATCH)。 方法一:使用 XML 的 <foreach> 标签ÿ…...

【JVM】Java虚拟机(二)——垃圾回收
目录 一、如何判断对象可以回收 (一)引用计数法 (二)可达性分析算法 二、垃圾回收算法 (一)标记清除 (二)标记整理 (三)复制 (四ÿ…...

Chrome 浏览器前端与客户端双向通信实战
Chrome 前端(即页面 JS / Web UI)与客户端(C 后端)的交互机制,是 Chromium 架构中非常核心的一环。下面我将按常见场景,从通道、流程、技术栈几个角度做一套完整的分析,特别适合你这种在分析和改…...

spring Security对RBAC及其ABAC的支持使用
RBAC (基于角色的访问控制) RBAC (Role-Based Access Control) 是 Spring Security 中最常用的权限模型,它将权限分配给角色,再将角色分配给用户。 RBAC 核心实现 1. 数据库设计 users roles permissions ------- ------…...
