【深度学习所有损失函数】在 NumPy、TensorFlow 和 PyTorch 中实现(1/2)
一、说明
在本文中,讨论了深度学习中使用的所有常见损失函数,并在NumPy,PyTorch和TensorFlow中实现了它们。
二、内容提要
我们本文所谈的代价函数如下所列:
- 均方误差 (MSE) 损失
- 二进制交叉熵损失
- 加权二进制交叉熵损失
- 分类交叉熵损失
- 稀疏分类交叉熵损失
- 骰子损失
- 吉隆坡背离损失
- 平均绝对误差 (MAE) / L1 损耗
- 胡贝尔损失
在下文,我们将逐一演示其不同实现办法。
三、均方误差 (MSE) 损失
均方误差 (MSE) 损失是回归问题中常用的损失函数,其目标是预测连续变量。损失计算为预测值和真实值之间的平方差的平均值。MSE 损失的公式为:
MSE loss = (1/n) * sum((y_pred — y_true)²)
这里:
- n 是数据集中的样本数
- 目标变量的预测值y_pred
- y_true是目标变量的真实值
MSE损失对异常值很敏感,并且会严重惩罚大误差,这在某些情况下可能是不可取的。在这种情况下,可以使用其他损失函数,如平均绝对误差(MAE)或Huber损失。
在 NumPy 中的实现
import numpy as npdef mse_loss(y_pred, y_true):"""Calculates the mean squared error (MSE) loss between predicted and true values.Args:- y_pred: predicted values- y_true: true valuesReturns:- mse_loss: mean squared error loss"""n = len(y_true)mse_loss = np.sum((y_pred - y_true) ** 2) / nreturn mse_loss 在此实现中,和 是分别包含预测值和真值的 NumPy 数组。该函数首先计算 和 之间的平方差,然后取这些值的平均值来获得 MSE 损失。该变量表示数据集中的样本数,用于规范化损失。y_predy_truey_predy_truen
TensorFlow 中的实现
import tensorflow as tfdef mse_loss(y_pred, y_true):"""Calculates the mean squared error (MSE) loss between predicted and true values.Args:- y_pred: predicted values- y_true: true valuesReturns:- mse_loss: mean squared error loss"""mse = tf.keras.losses.MeanSquaredError()mse_loss = mse(y_true, y_pred)return mse_loss在此实现中,和是分别包含预测值和真值的 TensorFlow 张量。该函数计算 和 之间的 MSE 损耗。该变量包含计算出的损失。y_predy_truetf.keras.losses.MeanSquaredError()y_predy_truemse_loss
在 PyTorch 中的实现
import torchdef mse_loss(y_pred, y_true):"""Calculates the mean squared error (MSE) loss between predicted and true values.Args:- y_pred: predicted values- y_true: true valuesReturns:- mse_loss: mean squared error loss"""mse = torch.nn.MSELoss()mse_loss = mse(y_pred, y_true)return mse_loss在此实现中,和 是分别包含预测值和真值的 PyTorch 张量。该函数计算 和 之间的 MSE 损耗。该变量包含计算出的损失。y_predy_truetorch.nn.MSELoss()y_predy_truemse_loss
四、二进制交叉熵损失
二进制交叉熵损失,也称为对数损失,是二元分类问题中使用的常见损失函数。它测量预测概率分布与实际二进制标签分布之间的差异。
二进制交叉熵损失的公式如下:
L(y, ŷ) = -[y * log(ŷ) + (1 — y) * log(1 — ŷ)]
其中 y 是真正的二进制标签(0 或 1),ŷ 是预测概率(范围从 0 到 1),log 是自然对数。
等式的第一项计算真实标签为 1 时的损失,第二项计算真实标签为 0 时的损失。总损失是两个项的总和。
当预测概率接近真实标签时,损失较低,当预测概率远离真实标签时,损失较高。此损失函数通常用于在输出层中使用 sigmoid 激活函数来预测二进制标签的神经网络模型。
4.1 在 NumPy 中的实现
在numpy中,二进制交叉熵损失可以使用我们前面描述的公式来实现。下面是如何计算它的示例:
# define true labels and predicted probabilities
y_true = np.array([0, 1, 1, 0])
y_pred = np.array([0.1, 0.9, 0.8, 0.3])# calculate the binary cross-entropy loss
loss = -(y_true * np.log(y_pred) + (1 - y_true) * np.log(1 - y_pred)).mean()# print the loss
print(loss)4.2 TensorFlow 中的实现
在 TensorFlow 中,二进制交叉熵损失可以使用 tf.keras.loss.BinaryCrossentropy() 函数实现。下面是如何使用它的示例:
import tensorflow as tf# define true labels and predicted probabilities
y_true = tf.constant([0, 1, 1, 0])
y_pred = tf.constant([0.1, 0.9, 0.8, 0.3])# define the loss function
bce_loss = tf.keras.losses.BinaryCrossentropy()# calculate the loss
loss = bce_loss(y_true, y_pred)# print the loss
print(loss)4.3 在 PyTorch 中的实现
在 PyTorch 中,二进制交叉熵损失可以使用该函数实现。下面是如何使用它的示例:torch.nn.BCELoss()
import torch# define true labels and predicted probabilities
y_true = torch.tensor([0, 1, 1, 0], dtype=torch.float32)
y_pred = torch.tensor([0.1, 0.9, 0.8, 0.3], dtype=torch.float32)# define the loss function
bce_loss = torch.nn.BCELoss()# calculate the loss
loss = bce_loss(y_pred, y_true)# print the loss
print(loss)4.4 加权二进制交叉熵损失
加权二元交叉熵损失是二元交叉熵损失的一种变体,允许为正熵和负示例分配不同的权重。这在处理不平衡的数据集时非常有用,其中一类与另一类相比明显不足。
加权二元交叉熵损失的公式如下:
L(y, ŷ) = -[w_pos * y * log(ŷ) + w_neg * (1 — y) * log(1 — ŷ)]
其中 y 是真正的二进制标签(0 或 1),ŷ 是预测概率(范围从 0 到 1),log 是自然对数,w_pos 和 w_neg 分别是正权重和负权重。
等式的第一项计算真实标签为 1 时的损失,第二项计算真实标签为 0 时的损失。总损失是两个项的总和,每个项按相应的权重加权。
可以根据每个类的相对重要性选择正权重和负权重。例如,如果正类更重要,则可以为其分配更高的权重。同样,如果负类更重要,则可以为其分配更高的权重。
当预测概率接近真实标签时,损失较低,当预测概率远离真实标签时,损失较高。此损失函数通常用于在输出层中使用 sigmoid 激活函数来预测二进制标签的神经网络模型。
五、分类交叉熵损失
分类交叉熵损失是多类分类问题中使用的一种常用损失函数。它衡量每个类的真实标签和预测概率之间的差异。
分类交叉熵损失的公式为:
L = -1/N * sum(sum(Y * log(Y_hat))) 其中 是单热编码格式的真实标签矩阵,是每个类的预测概率矩阵,是样本数,表示自然对数。YY_hatNlog
在此公式中,形状为 ,其中是样本数,是类数。每行 表示单个样本的真实标签分布,列中的值 1 对应于真实标签,0 对应于所有其他列。Y(N, C)NCY
类似地,具有 的形状,其中每行表示单个样本的预测概率分布,每个类都有一个概率值。Y_hat(N, C)
该函数逐个应用于预测的概率矩阵。该函数使用两次来求和矩阵的两个维度。logY_hatsumY
结果值表示数据集中所有样本的平均交叉熵损失。训练神经网络的目标是最小化这种损失函数。LN
损失函数对模型的惩罚更大,因为在预测低概率的类时犯了大错误。目标是最小化损失函数,这意味着使预测概率尽可能接近真实标签。
5.1 在 NumPy 中的实现
在numpy中,分类交叉熵损失可以使用我们前面描述的公式来实现。下面是如何计算它的示例:
import numpy as np# define true labels and predicted probabilities as NumPy arrays
y_true = np.array([[0, 1, 0], [0, 0, 1], [1, 0, 0]])
y_pred = np.array([[0.8, 0.1, 0.1], [0.2, 0.3, 0.5], [0.1, 0.6, 0.3]])# calculate the loss
loss = -1/len(y_true) * np.sum(np.sum(y_true * np.log(y_pred)))# print the loss
print(loss)In this example, y_true represents the true labels (in integer format), and y_pred represents the predicted probabilities for each class (in a 2D array). The eye() function is used to convert the true labels to one-hot encoding, which is required for the loss calculation. The categorical cross-entropy loss is calculated using the formula we provided earlier, and the mean() function is used to average the loss over the entire dataset. Finally, the calculated loss is printed to the console. 在此示例中, 以独热编码格式表示真实标签,并表示每个类的预测概率,两者都为 NumPy 数组。使用上述公式计算损失,然后使用该函数打印到控制台。请注意,该函数使用两次来对矩阵的两个维度求和。y_truey_predprintnp.sumY
5.2 TensorFlow 中的实现
在TensorFlow中,分类交叉熵损失可以使用该类轻松计算。下面是如何使用它的示例:tf.keras.losses.CategoricalCrossentropy
import tensorflow as tf# define true labels and predicted probabilities as TensorFlow Tensors
y_true = tf.constant([[0, 1, 0], [0, 0, 1], [1, 0, 0]])
y_pred = tf.constant([[0.8, 0.1, 0.1], [0.2, 0.3, 0.5], [0.1, 0.6, 0.3]])# create the loss object
cce_loss = tf.keras.losses.CategoricalCrossentropy()# calculate the loss
loss = cce_loss(y_true, y_pred)# print the loss
print(loss.numpy()) 在此示例中,以独热编码格式表示真实标签,并表示每个类的预测概率,两者都作为 TensorFlow 张量。该类用于创建损失函数的实例,然后通过将真实标签和预测概率作为参数传递来计算损失。最后,使用该方法将计算出的损失打印到控制台。y_truey_predCategoricalCrossentropy.numpy()
请注意,该类在内部处理将真实标签转换为独热编码,因此无需显式执行此操作。如果你的真实标签已经是独热编码格式,你可以将它们直接传递给损失函数,没有任何问题。CategoricalCrossentropy
5.3 在 PyTorch 中的实现
在 PyTorch 中,分类交叉熵损失可以使用该类轻松计算。下面是如何使用它的示例:torch.nn.CrossEntropyLoss
import torch# define true labels and predicted logits as PyTorch Tensors
y_true = torch.LongTensor([1, 2, 0])
y_logits = torch.Tensor([[0.8, 0.1, 0.1], [0.2, 0.3, 0.5], [0.1, 0.6, 0.3]])# create the loss object
ce_loss = torch.nn.CrossEntropyLoss()# calculate the loss
loss = ce_loss(y_logits, y_true)# print the loss
print(loss.item()) 在此示例中, 以整数格式表示真实标签,并表示每个类的预测对数,两者都作为 PyTorch 张量。该类用于创建损失函数的实例,然后通过将预测的对数和 true 标签作为参数传递来计算损失。最后,使用该方法将计算出的损失打印到控制台。y_truey_logitsCrossEntropyLoss.item()
请注意,该类将 softmax 激活函数和分类交叉熵损失组合到一个操作中,因此您无需单独应用 softmax。另请注意,真正的标签应采用整数格式,而不是独热编码格式。CrossEntropyLoss
相关文章:
)
【深度学习所有损失函数】在 NumPy、TensorFlow 和 PyTorch 中实现(1/2)
一、说明 在本文中,讨论了深度学习中使用的所有常见损失函数,并在NumPy,PyTorch和TensorFlow中实现了它们。 二、内容提要 我们本文所谈的代价函数如下所列: 均方误差 (MSE) 损失二进制交叉熵损失加权二进…...

七夕好物分享,哪些礼物适合送男/女朋友?这几款好物最为合适!
七夕是个值得纪念的日子,牛郎织女鹊桥相会的故事百年流传,七夕是一个表达爱意的节日,送礼物是必不可少的,情侣们可以选择一份有意义的礼物,也可以选择对方需要的东西当做礼物来赠送,总的来说,送…...

C语言学习系列-->看淡指针(2)
文章目录 前言一、数组名的理解二、使用指针访问数组三、一维数组传参本质四、二级指针五、指针数组六、指针数组模拟二维数组 前言 不把指针学的扎实,可不敢说自己C语言基础学的好 一、数组名的理解 #include <stdio.h> int main() {int arr[10] { 1,2,3,4…...

Java基础篇--Character 类
Character 类是用来操作单个字符的,它将 char 值包装在一个对象中。 实际上,在 Java 中,char 是基本数据类型,而 Character 是 char 的包装类。通过 Character 类,可以使用一系列方法来操作字符。在创建 Character 对…...

Flutter参考资料
Flutter 官网 : https://flutter.dev/ Flutter 插件下载地址 : https://pub.dev/packages Flutter 开发文档 : https://flutter.cn/docs ( 强烈推荐 ) 官方 GitHub 地址 : https://github.com/flutter Flutter 中文社区 : https://flutter.cn/ Flutter 实用教程 : https://flut…...

sed命令如何正确修改ini配置文件
需要保证key值的唯一性 function sed_key_value_file(){key$(echo "$1" | sed s/[\/&]/\\&/g)value$(echo "$2" | sed s/[\/&]/\\&/g)# 先删除原有的value,然后添加新的keyvaluesed -i -e "s#${key}.*#${key}${value}#&q…...

【新版系统架构补充】-信息系统基础知识
信息系统 信息系统的5个基本功能:输入、存储、处理、输出和控制 信息系统的分类(低级到高级):业务(数据)处理系统(TPS/DPS)、管理信息系统(MIS)、决策支持系…...
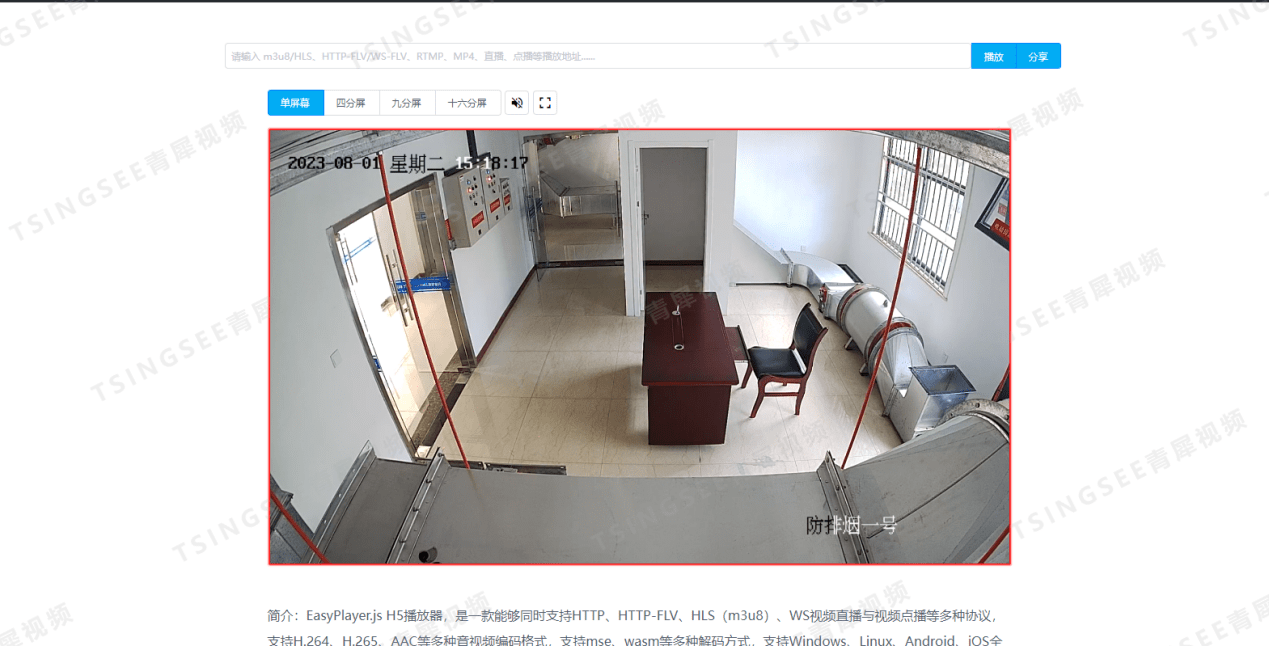
安防监控视频汇聚平台EasyCVR分发的FLV视频流在VLC中无法播放是什么原因?
众所周知,TSINGSEE青犀视频汇聚平台EasyCVR可支持多协议方式接入,包括主流标准协议国标GB28181、RTSP/Onvif、RTMP等,以及厂家私有协议与SDK接入,包括海康Ehome、海大宇等设备的SDK等。在视频流的处理与分发上,视频监控…...

前端遇到的面试题
1.水平垂直居中 绝对定位 transform position:absolute; top:50%; left:50%; transform:translate(-50%,-50%);绝对定位 margin(子元素宽高知道的情况下) position:absolute; top:50%; left:50%; margin-top:-100px; margin-left:-100px;绝对定位 margin:auto position:a…...
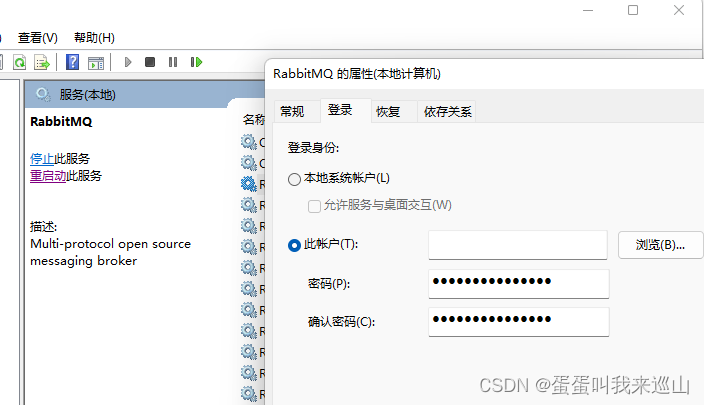
abbitmq启动访问不了http://localhost:15672 通过修改服务登录admin
abbitmq默认的对Administration授权,而我的用户不是默认的Administration,所以后来打开服务,找到rabbitmq服务,属性,登陆,将本地系统账户修改为此账户,修改完成之后再重启服务,这时候…...

换架 3D 飞机,继续飞呀飞
相信大多数图扑 HT 用户都曾见过这个飞机的 Demo,在图扑发展的这十年,这个 Demo 是许多学习 HT 用户一定会参考的经典 Demo 之一。 这个 Demo 用简洁的代码生动地展示了 OBJ 模型加载、数据绑定、动画和漫游等功能的实现。许多用户参考这个简单的 Demo 后…...

js ?? || 使用方法
平时很常用的就是||,比如调用接口的时候,接口报错了需要给个默认值 const data(await getData())||{};今天遇到了一个场景,正常后端返回的就是false,如果接口报错要默认设置成true,但如果用了 || ,如下,那…...

i茅台自动申购算法协议分析
首发地址:http://zhuoyue360.com/crack/104.html 一、引言 今日看到有人分享了i茅台自动申购的文章。但是它酷似引流文章,全文一张图,呜呜呜。无法白嫖。太可恶了,因此,我来啦~ 我来整一整,我也要抢茅子! …...
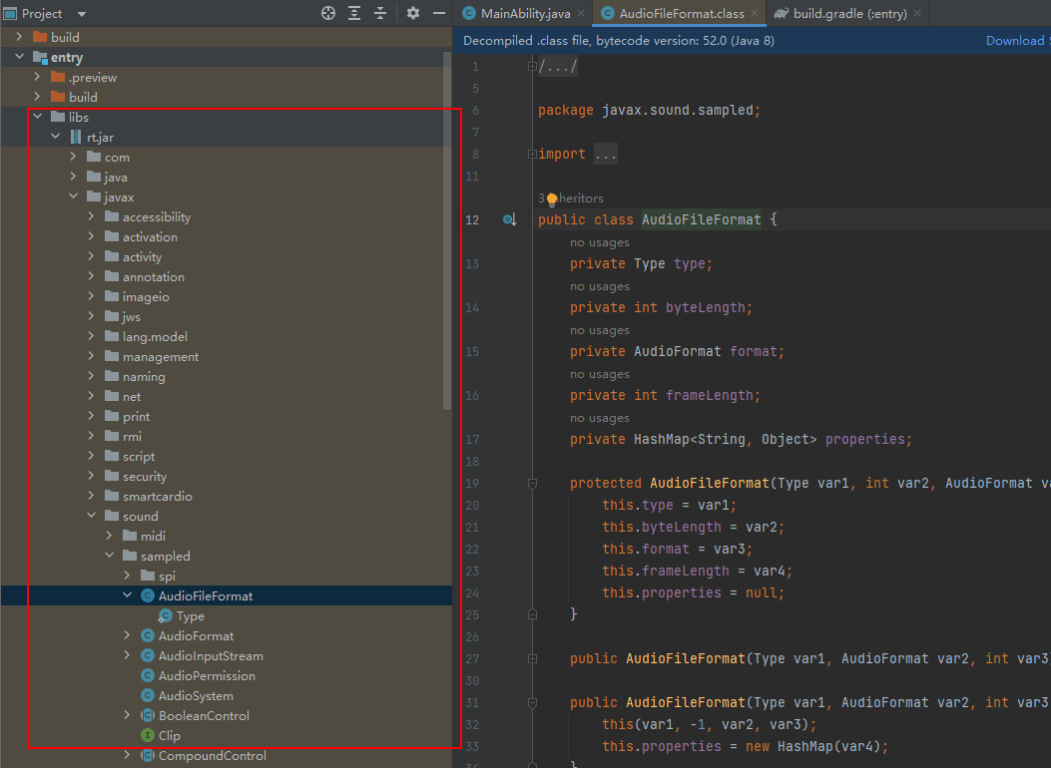
【HarmonyOS】Java如何引用外部jar包
【关键字】 Java、引用jar包 【写在前面】 使用API6和API7开发HarmonyOS应用时,因为应用中只能引用SDK中开放的功能接口,但是部分jdk自带的接口功能在SDK中并未封装,要想在工程中使用jdk开放的接口功能,需要将jdk中的jar包通过…...

vue在线编辑表格导入导出
npm i file-saver npm i exceljs npm i luckyexcelindex.html (方式一在html中引入) <link relstylesheet hrefhttps://cdn.jsdelivr.net/npm/luckysheetlatest/dist/plugins/css/pluginsCss.css /><link relstylesheet hrefhttps://cdn.jsde…...
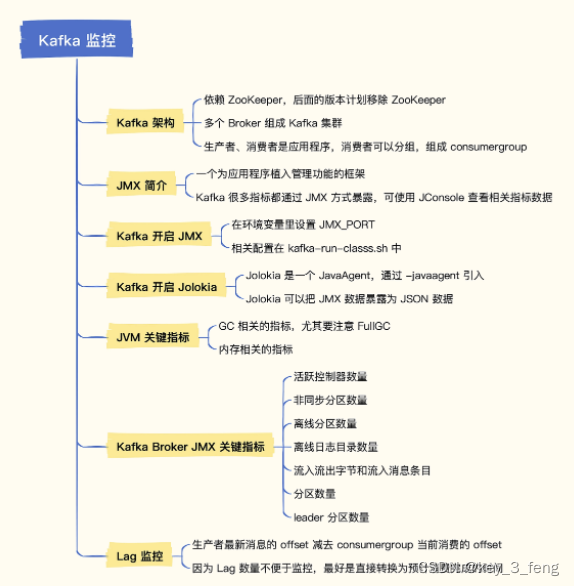
监控Kafka的关键指标
Kafka 架构 上面绿色部分 PRODUCER(生产者)和下面紫色部分 CONSUMER(消费者)是业务程序,通常由研发人员埋点解决监控问题,如果是 Java 客户端也会暴露 JMX 指标。组件运维监控层面着重关注蓝色部分的 BROKE…...

React18 hook学习笔记
useState useState用于在函数组件中声明和管理状态 它接受初始状态,并返回一个状态变量和一个更新状态的函数 通过调用更新状态的函数,可以改变状态的值并触发组件的重新渲染 import { useState } from "react"function App() {const [obj, …...

Java038——正则表达式
一、认识正则表达式 正则表达式通常被用于判断语句中,用来检查某一字符串是否满足某一格式。正则表达式是含有一些具有特殊意义字符的字符串,这些特殊字符称为正则表达式的元字符。例如,“\d”表示数字 0~9 中的任何一个,“d”就…...

JavaScript元素选择器
目录 一、getElementsByTagName1.说明2.用法示例 二、getElementsByName1.说明2.用法示例 三、getElementById1.说明2.用法示例 四、getElementsByClassName1.说明2.用法示例 五、querySelector1.说明2.用法示例 六、querySelectorAll1.说明2.用法示例 七、综合示例 一、getEle…...
Docker安装 elasticsearch-head
目录 前言安装elasticsearch-head步骤1:准备1. 安装docker2. 搜索可以使用的镜像。3. 也可从docker hub上搜索镜像。4. 选择合适的redis镜像。 步骤2:拉取elasticsearch-head镜像拉取镜像查看已拉取的镜像 步骤3:创建容器创建容器方式1&#…...

Lombok 的 @Data 注解失效,未生成 getter/setter 方法引发的HTTP 406 错误
HTTP 状态码 406 (Not Acceptable) 和 500 (Internal Server Error) 是两类完全不同的错误,它们的含义、原因和解决方法都有显著区别。以下是详细对比: 1. HTTP 406 (Not Acceptable) 含义: 客户端请求的内容类型与服务器支持的内容类型不匹…...
-----深度优先搜索(DFS)实现)
c++ 面试题(1)-----深度优先搜索(DFS)实现
操作系统:ubuntu22.04 IDE:Visual Studio Code 编程语言:C11 题目描述 地上有一个 m 行 n 列的方格,从坐标 [0,0] 起始。一个机器人可以从某一格移动到上下左右四个格子,但不能进入行坐标和列坐标的数位之和大于 k 的格子。 例…...

使用Matplotlib创建炫酷的3D散点图:数据可视化的新维度
文章目录 基础实现代码代码解析进阶技巧1. 自定义点的大小和颜色2. 添加图例和样式美化3. 真实数据应用示例实用技巧与注意事项完整示例(带样式)应用场景在数据科学和可视化领域,三维图形能为我们提供更丰富的数据洞察。本文将手把手教你如何使用Python的Matplotlib库创建引…...

浪潮交换机配置track检测实现高速公路收费网络主备切换NQA
浪潮交换机track配置 项目背景高速网络拓扑网络情况分析通信线路收费网络路由 收费汇聚交换机相应配置收费汇聚track配置 项目背景 在实施省内一条高速公路时遇到的需求,本次涉及的主要是收费汇聚交换机的配置,浪潮网络设备在高速项目很少,通…...

springboot整合VUE之在线教育管理系统简介
可以学习到的技能 学会常用技术栈的使用 独立开发项目 学会前端的开发流程 学会后端的开发流程 学会数据库的设计 学会前后端接口调用方式 学会多模块之间的关联 学会数据的处理 适用人群 在校学生,小白用户,想学习知识的 有点基础,想要通过项…...

排序算法总结(C++)
目录 一、稳定性二、排序算法选择、冒泡、插入排序归并排序随机快速排序堆排序基数排序计数排序 三、总结 一、稳定性 排序算法的稳定性是指:同样大小的样本 **(同样大小的数据)**在排序之后不会改变原始的相对次序。 稳定性对基础类型对象…...

沙箱虚拟化技术虚拟机容器之间的关系详解
问题 沙箱、虚拟化、容器三者分开一一介绍的话我知道他们各自都是什么东西,但是如果把三者放在一起,它们之间到底什么关系?又有什么联系呢?我不是很明白!!! 就比如说: 沙箱&#…...

解析两阶段提交与三阶段提交的核心差异及MySQL实现方案
引言 在分布式系统的事务处理中,如何保障跨节点数据操作的一致性始终是核心挑战。经典的两阶段提交协议(2PC)通过准备阶段与提交阶段的协调机制,以同步决策模式确保事务原子性。其改进版本三阶段提交协议(3PC…...

加密通信 + 行为分析:运营商行业安全防御体系重构
在数字经济蓬勃发展的时代,运营商作为信息通信网络的核心枢纽,承载着海量用户数据与关键业务传输,其安全防御体系的可靠性直接关乎国家安全、社会稳定与企业发展。随着网络攻击手段的不断升级,传统安全防护体系逐渐暴露出局限性&a…...

【HarmonyOS 5】鸿蒙中Stage模型与FA模型详解
一、前言 在HarmonyOS 5的应用开发模型中,featureAbility是旧版FA模型(Feature Ability)的用法,Stage模型已采用全新的应用架构,推荐使用组件化的上下文获取方式,而非依赖featureAbility。 FA大概是API7之…...
