第十三次CCF计算机软件能力认证
第一题:跳一跳
近来,跳一跳这款小游戏风靡全国,受到不少玩家的喜爱。
简化后的跳一跳规则如下:玩家每次从当前方块跳到下一个方块,如果没有跳到下一个方块上则游戏结束。
如果跳到了方块上,但没有跳到方块的中心则获得 1 分;跳到方块中心时,若上一次的得分为 1 分或这是本局游戏的第一次跳跃则此次得分为 2 分,否则此次得分比上一次得分多两分(即连续跳到方块中心时,总得分将 +2,+4,+6,+8…)。
现在给出一个人跳一跳的全过程,请你求出他本局游戏的得分(按照题目描述的规则)。
输入格式
输入包含多个数字,用空格分隔,每个数字都是 1,2,0 之一,1 表示此次跳跃跳到了方块上但是没有跳到中心,2 表示此次跳跃跳到了方块上并且跳到了方块中心,0 表示此次跳跃没有跳到方块上(此时游戏结束)。
输出格式
输出一个整数,为本局游戏的得分(在本题的规则下)。
数据范围
对于所有评测用例,输入的数字不超过 30 个,保证 0 正好出现一次且为最后一个数字。
输入样例:
1 1 2 2 2 1 1 2 2 0输出样例:
22
解题思路:
直接模拟
#include<iostream>using namespace std;int main()
{int last = 1;int n;int res = 0;while(cin >> n){if(n == 0) break;if(n == 1) res ++ , last = 1;else {if(last == -1 || last == 1) res += 2 , last = 2;else res += (last + 2) , last += 2;}}cout << res << endl;return 0;
}第二题:碰撞的小球
数轴上有一条长度为 L(L 为偶数)的线段,左端点在原点,右端点在坐标 L 处。
有 n 个不计体积的小球在线段上,开始时所有的小球都处在偶数坐标上,速度方向向右,速度大小为 1 单位长度每秒。
当小球到达线段的端点(左端点或右端点)的时候,会立即向相反的方向移动,速度大小仍然为原来大小。
当两个小球撞到一起的时候,两个小球会分别向与自己原来移动的方向相反的方向,以原来的速度大小继续移动。
现在,告诉你线段的长度 L,小球数量 n ,以及 n 个小球的初始位置,请你计算 t 秒之后,各个小球的位置。
提示
因为所有小球的初始位置都为偶数,而且线段的长度为偶数,可以证明,不会有三个小球同时相撞,小球到达线段端点以及小球之间的碰撞时刻均为整数。
同时也可以证明两个小球发生碰撞的位置一定是整数(但不一定是偶数)。
输入格式
输入的第一行包含三个整数 n,L,t,用空格分隔,分别表示小球的个数、线段长度和你需要计算 t 秒之后小球的位置。
第二行包含 n 个整数 a1,a2,…,an,用空格分隔,表示初始时刻 n 个小球的位置。
输出格式
输出一行包含 n 个整数,用空格分隔,第 i 个整数代表初始时刻位于 ai 的小球,在 t 秒之后的位置。
数据范围
对于所有评测用例,1≤n≤100,1≤t≤100,2≤L≤1000,0<ai<L。L 为偶数。
保证所有小球的初始位置互不相同且均为偶数。
输入样例1:
3 10 5 4 6 8输出样例1:
7 9 9样例1解释
初始时,三个小球的位置分别为 4,6,8。
一秒后,三个小球的位置分别为 5,7,9。
两秒后,第三个小球碰到墙壁,速度反向,三个小球位置分别为 6,8,10。
三秒后,第二个小球与第三个小球在位置 9 发生碰撞,速度反向(注意碰撞位置不一定为偶数),三个小球位置分别为 7,9,9。
四秒后,第一个小球与第二个小球在位置8发生碰撞,速度反向,第三个小球碰到墙壁,速度反向,三个小球位置分别为 8,8,10。
五秒后,三个小球的位置分别为 7,9,9。
输入样例2:
10 22 30 14 12 16 6 10 2 8 20 18 4输出样例2:
6 6 8 2 4 0 4 12 10 2
解题思路:
使用结构体存储小球当前的状态 +1 表示向右 , -1表示向左
第一种情况,到边界的时候将方向置反即可
第二种情况,正常运动时
(1)下一秒的时候没有遇到球,当前位置加上方向信息
(2)下一秒的时候遇到球的时候,将两个球反向
#include<iostream>
#include<cstring>using namespace std;const int N = 110;
int n , l , t;
struct node
{int idx , dir; // +1 表示向右 , -1表示向左
}a[N];void change()
{int cnt[10 * N];memset(cnt , -1 , sizeof cnt);for(int i = 0;i < n;i ++){if(a[i].idx == 0 || a[i].idx == l) a[i].dir = -a[i].dir;if(cnt[a[i].idx] != -1){a[i].dir = -a[i].dir;a[cnt[a[i].idx]].dir = -a[cnt[a[i].idx]].dir;}else cnt[a[i].idx] = i;}for(int i = 0;i < n;i ++)a[i].idx += a[i].dir;
}int main()
{cin >> n >> l >> t;for(int i = 0;i < n;i ++){int x;cin >> x;a[i] = {x , 1};}while(t --){change();}for(int i = 0;i < n;i ++)cout << a[i].idx << " ";return 0;
}第三题:URL映射
题目略
解题思路:
其中三个重要的函数
(1)get_number函数:获取字符串中的数字并且返回该数的字符串
(2)get函数:将每一条URL映射解析
- 如果匹配,那么返回一个vector存储的是对应URL请求的解析后的结果
- 如果不匹配, 那么返回一个空的vector
(3)work函数:尽心处理每一条URL请求
#include <iostream>
#include <cstring>
#include <algorithm>
#include <vector>using namespace std;const int N = 110;int n, m;
struct Url
{string path, name;
}url[N];string get_number(string& str)
{string res;for (auto c: str)if (c >= '0' && c <= '9')res += c;else{res.clear();return res;}// 去掉前导0int k = 0;while (k + 1 < res.size() && res[k] == '0') k ++ ;return res.substr(k);
}vector<string> get(string& path, string& str)
{vector<string> res(1);int i, j;for (i = 1, j = 1; i < path.size() && j < str.size();){int u = i + 1, v = j + 1;while (u < path.size() && path[u] != '/') u ++ ;while (v < str.size() && str[v] != '/') v ++ ;string a = path.substr(i, u - i), b = str.substr(j, v - j);if (a == "<str>"){res.push_back(b);i = u + 1, j = v + 1;}else if (a == "<int>"){auto t = get_number(b);if (t.empty()){res.clear();return res;}res.push_back(t);i = u + 1, j = v + 1;}else if (a == "<path>"){res.push_back(str.substr(j));return res;}else if (a != b){res.clear();return res;}else i = u + 1, j = v + 1;}if (i - path.size() != j - str.size()) res.clear();return res;
}void work(string& str)
{for (int i = 0; i < n; i ++ ){auto res = get(url[i].path, str);if (res.size()){cout << url[i].name;for (int j = 1; j < res.size(); j ++ )cout << ' ' << res[j];cout << endl;return;}}puts("404");
}int main()
{cin >> n >> m;for (int i = 0; i < n; i ++ ) cin >> url[i].path >> url[i].name;while (m -- ){string str;cin >> str;work(str);}return 0;
}第四题:棋局评估
Alice 和 Bob 正在玩井字棋游戏。
井字棋游戏的规则很简单:两人轮流往 3×3 的棋盘中放棋子,Alice 放的是
X,Bob 放的是O,Alice执先。当同一种棋子占据一行、一列或一条对角线的三个格子时,游戏结束,该种棋子的持有者获胜。
当棋盘被填满的时候,游戏结束,双方平手。
Alice 设计了一种对棋局评分的方法:
- 对于 Alice 已经获胜的局面,评估得分为(棋盘上的空格子数+1);
- 对于 Bob 已经获胜的局面,评估得分为 -(棋盘上的空格子数+1);
- 对于平局的局面,评估得分为 0;
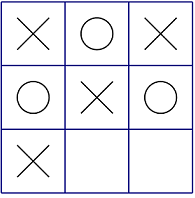
例如上图中的局面,Alice 已经获胜,同时棋盘上有 2 个空格,所以局面得分为 2+1=3。
由于 Alice 并不喜欢计算,所以他请教擅长编程的你,如果两人都以最优策略行棋,那么当前局面的最终得分会是多少?
输入格式
输入的第一行包含一个正整数 T,表示数据的组数。
每组数据输入有 3 行,每行有 3 个整数,用空格分隔,分别表示棋盘每个格子的状态。0 表示格子为空,1 表示格子中为
X,2 表示格子中为O。保证不会出现其他状态。保证输入的局面合法。(即保证输入的局面可以通过行棋到达,且保证没有双方同时获胜的情况)
保证输入的局面轮到 Alice 行棋。
输出格式
对于每组数据,输出一行一个整数,表示当前局面的得分。
数据范围
1≤T≤5
输入样例:
3 1 2 1 2 1 2 0 0 0 2 1 1 0 2 1 0 0 2 0 0 0 0 0 0 0 0 0输出样例:
3 -4 0样例解释
第一组数据:
Alice 将棋子放在左下角(或右下角)后,可以到达问题描述中的局面,得分为 3。
3 为 Alice 行棋后能到达的局面中得分的最大值。
第二组数据:
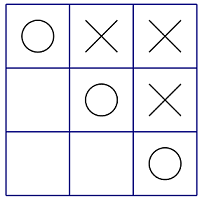
Bob 已经获胜(如图),此局面得分为 −(3+1)=−4。
第三组数据:
井字棋中若双方都采用最优策略,游戏平局,最终得分为 0。
解题思路:
其中有三个函数
(1)dfs函数:求最终的得分,使用深度优先搜索进行遍历每一种情况
(2)cal函数:计算每一个状态时的空格的数量
(3)check函数:对于一个人判断是否是一个获胜的情况
#include<iostream>using namespace std;const int N = 5 , INF = 1e8;
int g[N][N];bool check(int x)
{// 判断行列for(int i = 0;i < 3;i ++){int s = 0;for(int j = 0;j < 3;j ++)if(g[i][j] == x) s ++;if(s == 3) return true;s = 0;for(int j = 0;j < 3;j ++)if(g[j][i] == x) s ++;if(s == 3) return true;}if(g[0][0] == x && g[1][1] == x && g[2][2] == x) return true;if(g[2][0] == x && g[1][1] == x && g[0][2] == x) return true;return false;
}int cal()
{int s = 0;// 计算空格的数量for(int i = 0;i < 3;i ++)for(int j = 0;j < 3;j ++)if(!g[i][j]) s ++;// alice赢if(check(1)) return s + 1;// bob赢if(check(2)) return -(s + 1);// 平局if(!s) return 0;return INF;
}int dfs(int u)
{int t = cal();if(t != INF) return t;if(!u){// alice 搜索最大值 X 使用1表示int res = -INF;for(int i = 0;i < 3;i ++)for(int j = 0;j < 3;j ++)if(!g[i][j]){g[i][j] = 1;res = max(res , dfs(1));g[i][j] = 0;}return res;}else{// bob 搜索最小值 O 使用2表示int res = INF;for(int i = 0;i < 3;i ++)for(int j = 0;j < 3;j ++)if(!g[i][j]){g[i][j] = 2;res = min(res , dfs(0));g[i][j] = 0;}return res;}
}int main()
{int t;cin >> t;while(t --){for(int i = 0;i < 3;i ++)for(int j = 0;j < 3;j ++)cin >> g[i][j];// 0表示alice 1表示bobcout << dfs(0) << endl;}
}第五题:二次求和
线段树+前缀和+树
(不会)
#include <iostream>
#include <cstring>
#include <algorithm>using namespace std;typedef long long LL;
const int N = 100010, M = N * 2, MOD = 1e9 + 7;int n, m, L, R;
int w[N];
int h[N], father[N], e[M], ne[M], idx;
int depth[N], fa[N][17];
int path[N], d[N], que[N];
int pos[N], root[N];
bool st[N];
int tr[N];
struct Node
{int d, w, id;bool operator< (const Node& t) const{return d < t.d;}
}q[N], p[N];inline void add(int a, int b)
{e[idx] = b, ne[idx] = h[a], h[a] = idx ++ ;
}inline int lowbit(int x)
{return x & -x;
}inline void update(int x, int v, int k)
{for (int i = x; i <= k; i += lowbit(i)) tr[i] = (tr[i] + v) % MOD;
}inline int query(int x, int k)
{x = min(x, k);int res = 0;for (int i = x; i > 0; i -= lowbit(i)) res = (res + tr[i]) % MOD;return res;
}void bfs()
{memset(depth, 0x3f, sizeof depth);depth[0] = 0, depth[1] = 1;int hh = 0, tt = 0;que[0] = 1;while (hh <= tt){int t = que[hh ++ ];for (int i = h[t]; ~i; i = ne[i]){int j = e[i];if (depth[j] > depth[t] + 1){depth[j] = depth[t] + 1;que[ ++ tt] = j;fa[j][0] = t;for (int k = 1; k <= 16; k ++ )fa[j][k] = fa[fa[j][k - 1]][k - 1];}}}
}inline int lca(int a, int b)
{if (depth[a] < depth[b]) swap(a, b);for (int k = 16; k >= 0; k -- )if (depth[fa[a][k]] >= depth[b])a = fa[a][k];if (a == b) return a;for (int k = 16; k >= 0; k -- )if (fa[a][k] != fa[b][k]){a = fa[a][k];b = fa[b][k];}return fa[a][0];
}void dfs(int u, int fa)
{d[u] = (d[fa] + path[u]) % MOD;for (int i = h[u]; ~i; i = ne[i]){int j = e[i];if (j == fa) continue;dfs(j, u);}
}int get_size(int u, int fa)
{if (st[u]) return 0;int res = 1;for (int i = h[u]; ~i; i = ne[i])if (e[i] != fa)res += get_size(e[i], u);return res;
}int get_wc(int u, int fa, int tot, int& wc)
{if (st[u]) return 0;int sum = 1, ms = 0;for (int i = h[u]; ~i; i = ne[i]){int j = e[i];if (j == fa) continue;int t = get_wc(j, u, tot, wc);ms = max(ms, t);sum += t;}ms = max(ms, tot - sum);if (ms <= tot / 2) wc = u;return sum;
}void get_dist(int u, int fa, int dist, int sum, int& qt)
{if (st[u]) return;q[ ++ qt] = {dist, sum, u};for (int i = h[u]; ~i; i = ne[i]){int j = e[i];if (j != fa)get_dist(j, u, dist + 1, (sum + w[j]) % MOD, qt);}
}inline int get(Node a[], int k, int limit, int wu, int& pu)
{sort(a + 1, a + k + 1);static int sum[N];int res = 0;for (int i = 1; i <= k; i ++ ) sum[i] = (sum[i - 1] + a[i].w) % MOD;for (int i = 1, j = k; i < j; i ++ ){while (j > i && a[j].d + a[i].d - 1 > limit) j -- ;if (j > i && a[j].d + a[i].d - 1 <= limit){res = (res + (LL)sum[j] - sum[i] + (LL)(j - i) * a[i].w - (LL)wu * (j - i)) % MOD;pu = (pu + j - i) % MOD;}}return res;
}int dfs_path(int u, int fa, int dist, int maxd)
{if (st[u]) return 0;int res = (query(R + 1 - dist, maxd) - query(L - dist, maxd)) % MOD;if (dist >= L && dist <= R) res = (res + 1) % MOD;for (int i = h[u]; ~i; i = ne[i]){int j = e[i];if (j != fa)res = (res + dfs_path(j, u, dist + 1, maxd)) % MOD;}path[u] = (path[u] + res) % MOD;return res;
}int calc(int u)
{if (st[u]) return 0;get_wc(u, -1, get_size(u, -1), u);st[u] = true;int res = 0, pt = 0;if (L <= 1 && R >= 1) res = w[u], path[u] = (path[u] + 1) % MOD;int cnt = 0, maxd = 0;for (int i = h[u]; ~i; i = ne[i]){int j = e[i], qt = 0;if (st[j]) continue;get_dist(j, -1, 2, (w[u] + w[j]) % MOD, qt);int pR = 0, pL = 0;res = (res - (LL)(get(q, qt, R, w[u], pR) - get(q, qt, L - 1, w[u], pL))) % MOD;path[u] = (path[u] - (LL)(pR - pL)) % MOD;pos[ ++ cnt] = pt + 1; // 每一段开头root[cnt] = j; // 每一段的根节点for (int k = 1; k <= qt; k ++ ){if (q[k].d >= L && q[k].d <= R){res = (res + q[k].w) % MOD;path[u] = (path[u] + 1) % MOD; // 只计算从u到当前点的}p[ ++ pt] = q[k];maxd = max(maxd, q[k].d);}}pos[cnt + 1] = pt + 1; // 哨兵for (int i = 1; i <= maxd; i ++ ) tr[i] = 0;for (int i = 1; i <= pt; i ++ ) update(p[i].d, 1, maxd); // 插入树状数组中for (int i = 1; i <= cnt; i ++ ){int l = pos[i], r = pos[i + 1] - 1;for (int j = l; j <= r; j ++ ) update(p[j].d, -1, maxd); // 将当前子树中的节点删掉dfs_path(root[i], u, 2, maxd);for (int j = l; j <= r; j ++ ) update(p[j].d, 1, maxd); // 将当前子树中的节点添加回来}int pR = 0, pL = 0;res = (res + (LL)get(p, pt, R, w[u], pR) - get(p, pt, L - 1, w[u], pL)) % MOD;path[u] = (path[u] + (LL)pR - pL) % MOD;for (int i = h[u]; ~i; i = ne[i]) res = (res + calc(e[i])) % MOD;return res;
}int main()
{int T;scanf("%d", &T);while (T -- ){scanf("%d%d%d%d", &n, &m, &L, &R);memset(h, -1, sizeof h), idx = 0;memset(path, 0, sizeof path);for (int i = 1; i <= n; i ++ ) scanf("%d", &w[i]);for (int i = 2; i <= n; i ++ ){int p;scanf("%d", &p);add(i, p), add(p, i);father[i] = p;}memset(st, 0, sizeof st);int res = calc(1);dfs(1, 0);bfs();while (m -- ){int a, b, c;scanf("%d%d%d", &a, &b, &c);int p = lca(a, b);int sum = (d[a] + (LL)d[b] - d[p] * 2 + path[p]) * c % MOD;res = ((res + sum) % MOD + MOD) % MOD;printf("%d\n", res);}}return 0;
}
相关文章:
第十三次CCF计算机软件能力认证
第一题:跳一跳 近来,跳一跳这款小游戏风靡全国,受到不少玩家的喜爱。 简化后的跳一跳规则如下:玩家每次从当前方块跳到下一个方块,如果没有跳到下一个方块上则游戏结束。 如果跳到了方块上,但没有跳到方块的…...

无人驾驶实战-第十二课(强化学习自动驾驶系统)(完)
在七月算法上报了《无人驾驶实战》课程,老师讲的真好。好记性不如烂笔头,记录一下学习内容。 课程入口,感兴趣的也可以跟着学一下。 ————————————————————————————————————————— 强化学习ÿ…...

【flask sqlalchmey】一次性将返回的列表对象或者 一行数据对象转成dict---flask-sqlalchemy输出json格式数据
def model_to_dict(object):return {c.name: getattr(object, c.name) for c in object.__table__.columns}#将一组数据转为list def scalars_to_list(object):return [model_to_dict(c) for c in object]class Sysdict(Base,SerializerMixin):__bind_key__ forest_fire_contr…...
goland插件推荐Rider UI Theme Pack
推荐一个goland配色插件Rider UI Theme Pack,里面自带visual assist配色,配色截图如下: 直接在plugins里面进行搜索或者在插件home page下载后进行安装均可。 总算找到一统vscode 和goland二者优势的插件了。...

人工智能面试常识-10
目录 1. 人工智能的常见用途和应用有哪些? 2. 什么是智能代理,它们如何在人工智能中使用?...
Android JNI开发从0到1,java调C,C调Java,保姆级教程详解
前些天发现了一个蛮有意思的人工智能学习网站,8个字形容一下"通俗易懂,风趣幽默",感觉非常有意思,忍不住分享一下给大家。 👉点击跳转到教程 第一步首先配置Android studio的NDK开发环境,首先在Android studio中下载NDK…...
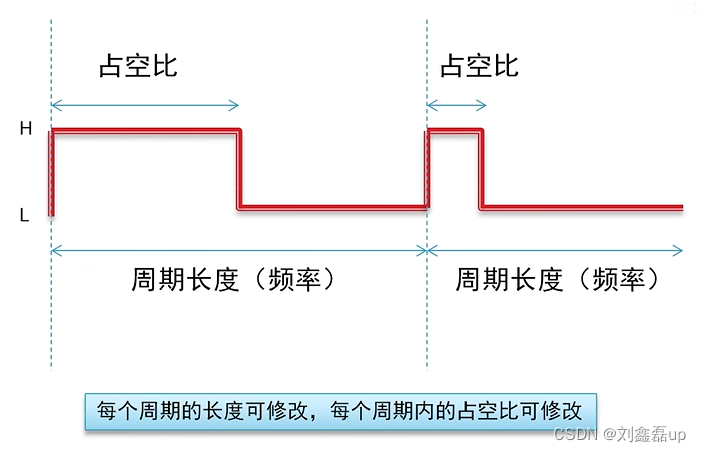
STM32基于CubeIDE和HAL库 基础入门学习笔记:功能驱动与应用
文章目录: 一:LED与按键驱动程序 main.c 1.闪灯 led.h led.c 2.按键控制LED亮灭 key.h key.c 二:蜂鸣器与继电器驱动程序 main.c 1.蜂鸣器 buzzer.h buzzer.c delay.h delay.c 2.继电器 relay.h relay.c 三࿱…...
 玄子Share 设计模式 GOF 全23种 + 七大设计原则)
创建型模式 (Creational Patterns) 玄子Share 设计模式 GOF 全23种 + 七大设计原则
玄子Share 设计模式 GOF 全23种 七大设计原则 [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-NWLAOFtO-1691793071647)(./assets/%E7%8E%84%E5%AD%90Share%20%E8%AE%BE%E8%AE%A1%E6%A8%A1%E5%BC%8F%20GOF%20%E5%85%A823%E7%A7%8D%20%20%E4%B8%83%E…...
【脚踢数据结构】队列(顺序和链式)
(꒪ꇴ꒪ ),Hello我是祐言QAQ我的博客主页:C/C语言,Linux基础,ARM开发板,软件配置等领域博主🌍快上🚘,一起学习,让我们成为一个强大的攻城狮!送给自己和读者的一句鸡汤🤔&…...
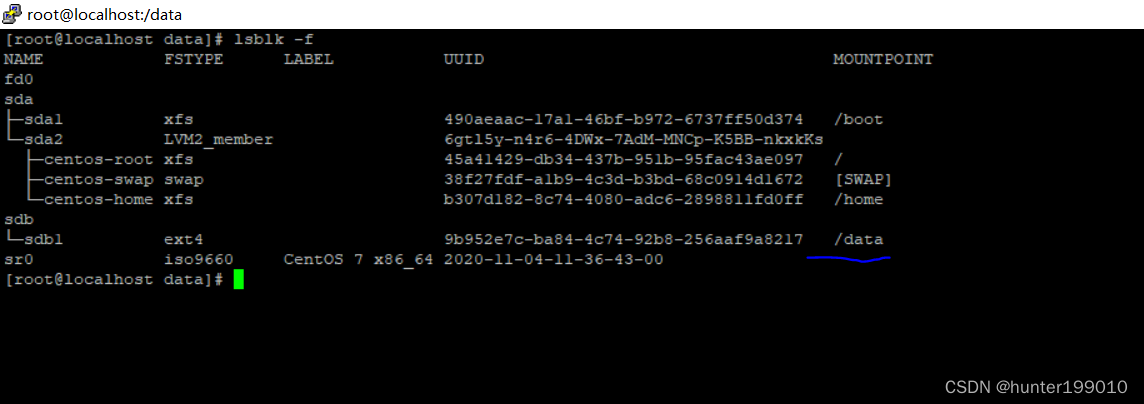
linux添加磁盘
一、linux虚拟机添加一块新的硬盘 四步: (1) (2)为硬盘进行分区 (3)初始化硬盘分区 (4)挂载 在虚拟机上添加一块硬盘 (1)、 虚拟机添加一块新的硬盘作为数据盘 (2) ls…...
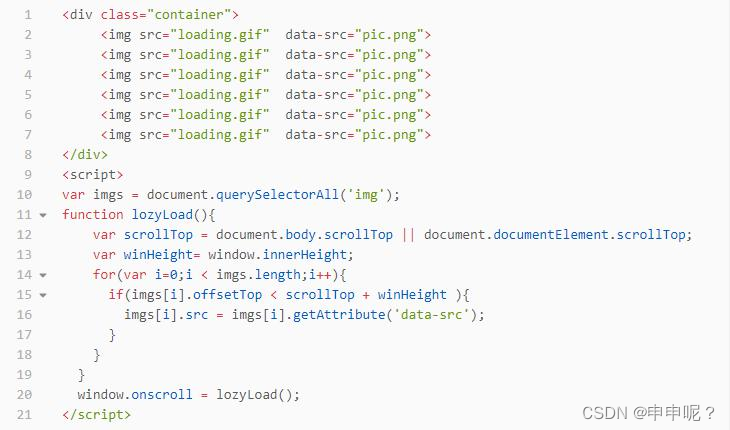
图片懒加载
什么是图片懒加载? 懒加载也叫做延迟加载、按需加载,指的是在长网页中延迟加载图片 数据,是一种较好的网页性能优化的方式。在比较长的网页或应用中, 如果图片很多,所有的图片都被加载出来,而用户只能看到可…...
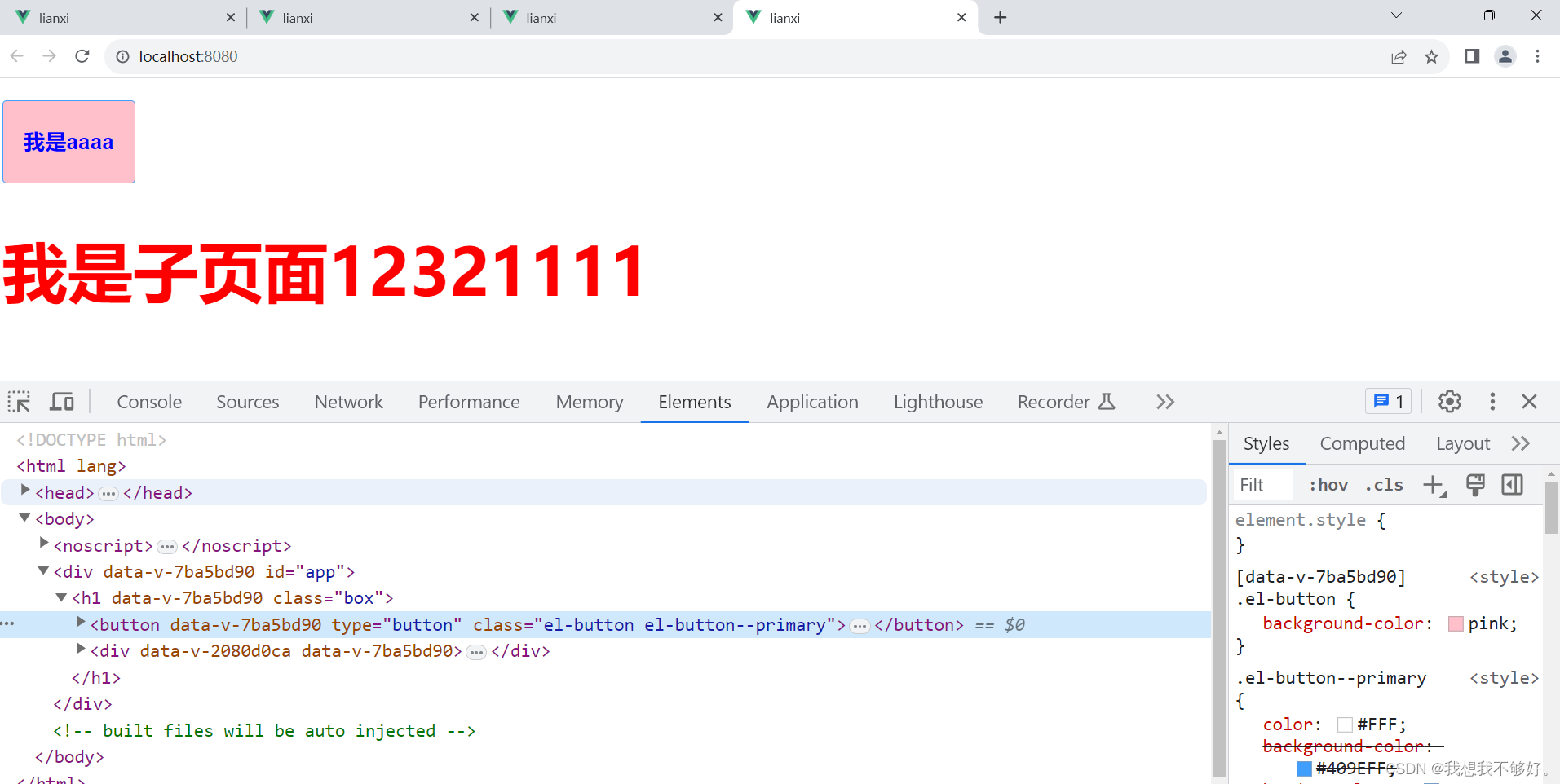
scope,deep穿透的实际应用
一.父组件代码 <template><div id"app"><h1 class"box"><pageName> </pageName></h1></div> </template><script> import pageName from "../src/components/pageName.vue"; export de…...
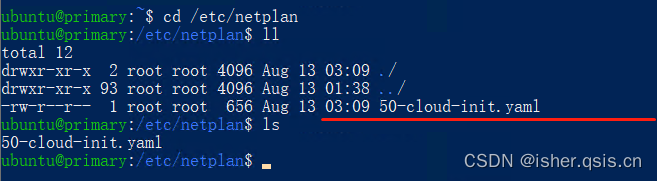
Multipass虚拟机设置局域网固定IP同时实现快速openshell的链接
本文只介绍在windows下实现的过程,Ubuntu采用22.04 安装multipass后,在卓面右下角Open shell 就可以链接默认实例Primary,当然如果你有多个虚拟机,可以针对不同内容单独建立终端的链接,而本文仅仅用Primary来说明。 …...

Webpack5 core-js和babel-loader区别和用法
文章目录 core-js是什么,有什么用?为什么使用了babel-loader对js进行兼容性配置还需要core-js?core-js的具体用法总结 core-js是什么,有什么用? core-js是一个流行的JavaScript库,它提供了对新的JavaScript特性、API…...
软考高级架构师——5、系统规划分析与设计方法
系统计划主要用于描述从项目提出、选择到确立的过程,包括系统项目的提出与可行性 分析,系统方案的制订、评价和改进,新旧系统的分析和比较,以及现有软件、硬件和数据 资源的有效利用等问题。 1、项目的提出与选择 项目的立项目标…...
区块链学习6-长安链部署:如何创建特定共识节点数和同步节点数的链
正常prepare的时候只支持4 7 13 16个节点个数,想要创建10个节点,其中5个是共识节点,如何实现? 1. 注释掉prepare.sh的这几行: 2. 修改 crytogen的模板文件: 如果是cert模式:chainmaker-crypt…...

北航基于openEuler构建工业机器人操作系统,打造“开箱即用”的机器人基础软件平台
北京航空航天大学是国家“双一流”建设高校,以建设扎根中国大地的世界一流大学为发展目标。北京航空航天大学在机器人领域一直处于行业前沿,以其亮眼的成果和优秀的师资力量,成为国内机器人领域的重要参与者和建设者。机器人操作系统是机器人…...
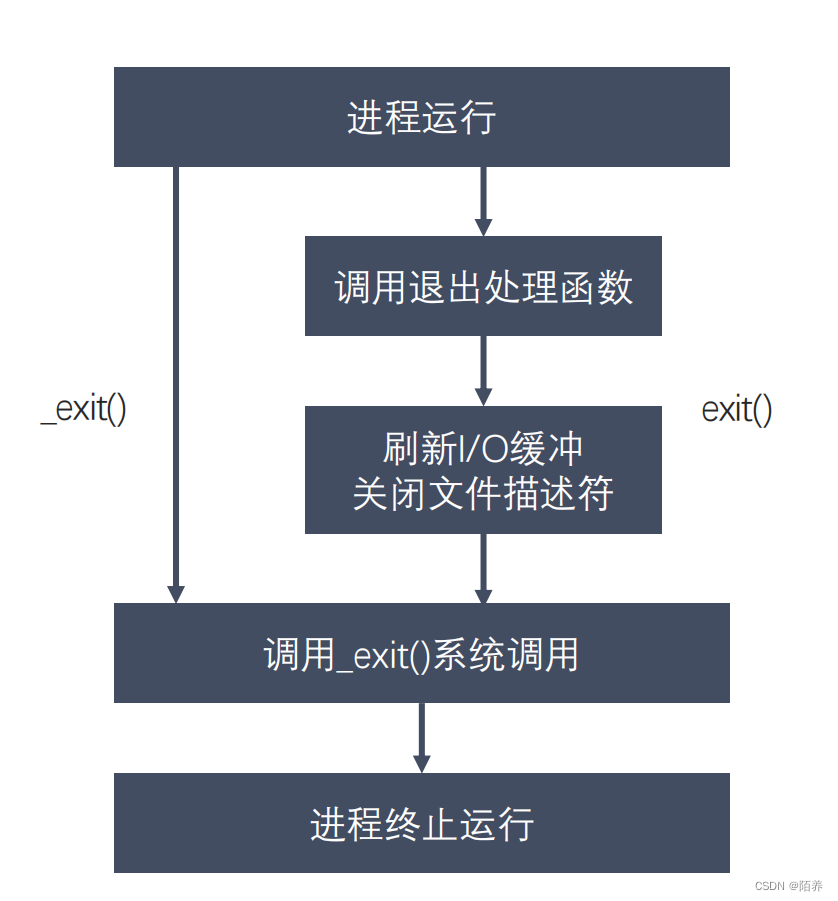
孤儿进程与僵尸进程
进程退出 关于进程退出有两个函数 exit和 _exit:其主要差别是在于是否直接退出。 其流程主要区别如下: 孤儿进程(不存在危害) 父进程运行结束,但子进程还在运行(未运行结束),这…...

redis的基础命令01
1、操作库的指令 1、清除当前库---flushdb 2、清除所有库---flushAll 2、操作key的指令 最常用的指令get、set 1)set key value 2)get key 基础指令 1、del 删除单个:del key 、批量删除:del key1 key2 key3 2、exists 判断key是否…...

批量将excel文件合并
要批量合并多个Excel文件,可以按照以下步骤进行操作: 1. 导入所需的Python库:首先,您需要导入pandas库来处理Excel文件。 import pandas as pd 2. 定义文件路径和输出文件名称: input_folder "your_input_fo…...

【大模型RAG】拍照搜题技术架构速览:三层管道、两级检索、兜底大模型
摘要 拍照搜题系统采用“三层管道(多模态 OCR → 语义检索 → 答案渲染)、两级检索(倒排 BM25 向量 HNSW)并以大语言模型兜底”的整体框架: 多模态 OCR 层 将题目图片经过超分、去噪、倾斜校正后,分别用…...

k8s从入门到放弃之Ingress七层负载
k8s从入门到放弃之Ingress七层负载 在Kubernetes(简称K8s)中,Ingress是一个API对象,它允许你定义如何从集群外部访问集群内部的服务。Ingress可以提供负载均衡、SSL终结和基于名称的虚拟主机等功能。通过Ingress,你可…...

Mac下Android Studio扫描根目录卡死问题记录
环境信息 操作系统: macOS 15.5 (Apple M2芯片)Android Studio版本: Meerkat Feature Drop | 2024.3.2 Patch 1 (Build #AI-243.26053.27.2432.13536105, 2025年5月22日构建) 问题现象 在项目开发过程中,提示一个依赖外部头文件的cpp源文件需要同步,点…...

Web 架构之 CDN 加速原理与落地实践
文章目录 一、思维导图二、正文内容(一)CDN 基础概念1. 定义2. 组成部分 (二)CDN 加速原理1. 请求路由2. 内容缓存3. 内容更新 (三)CDN 落地实践1. 选择 CDN 服务商2. 配置 CDN3. 集成到 Web 架构 …...

回溯算法学习
一、电话号码的字母组合 import java.util.ArrayList; import java.util.List;import javax.management.loading.PrivateClassLoader;public class letterCombinations {private static final String[] KEYPAD {"", //0"", //1"abc", //2"…...

推荐 github 项目:GeminiImageApp(图片生成方向,可以做一定的素材)
推荐 github 项目:GeminiImageApp(图片生成方向,可以做一定的素材) 这个项目能干嘛? 使用 gemini 2.0 的 api 和 google 其他的 api 来做衍生处理 简化和优化了文生图和图生图的行为(我的最主要) 并且有一些目标检测和切割(我用不到) 视频和 imagefx 因为没 a…...

安全突围:重塑内生安全体系:齐向东在2025年BCS大会的演讲
文章目录 前言第一部分:体系力量是突围之钥第一重困境是体系思想落地不畅。第二重困境是大小体系融合瓶颈。第三重困境是“小体系”运营梗阻。 第二部分:体系矛盾是突围之障一是数据孤岛的障碍。二是投入不足的障碍。三是新旧兼容难的障碍。 第三部分&am…...

GruntJS-前端自动化任务运行器从入门到实战
Grunt 完全指南:从入门到实战 一、Grunt 是什么? Grunt是一个基于 Node.js 的前端自动化任务运行器,主要用于自动化执行项目开发中重复性高的任务,例如文件压缩、代码编译、语法检查、单元测试、文件合并等。通过配置简洁的任务…...

【无标题】路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论
路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论 一、传统路径模型的根本缺陷 在经典正方形路径问题中(图1): mermaid graph LR A((A)) --- B((B)) B --- C((C)) C --- D((D)) D --- A A -.- C[无直接路径] B -…...
的使用)
Go 并发编程基础:通道(Channel)的使用
在 Go 中,Channel 是 Goroutine 之间通信的核心机制。它提供了一个线程安全的通信方式,用于在多个 Goroutine 之间传递数据,从而实现高效的并发编程。 本章将介绍 Channel 的基本概念、用法、缓冲、关闭机制以及 select 的使用。 一、Channel…...