数据挖掘全流程解析
数据挖掘全流程解析
数据指标选择
在这一阶段,使用直方图和柱状图的方式对数据进行分析,观察什么数据属性对于因变量会产生更加明显的结果。
如何绘制直方图和条形统计图
数据清洗
观察数据是否存在数据缺失或者离群点的情况。
数据异常的两种情况 :
1、不完整(缺少属性值)
2、含有噪音数据(错误或者离群)
缺失数据的处理方法:
1、忽略元组(当每个属性的缺失值比例比较大时,效果非常差,直接删除处理)
2、手动填写缺失值(工作量会比较大)
3、自动填写(使用属性的缺失值进行填充,仅对于连续性数值类型的数值适用),假如数据是离散标签类型数据,则使用相应的众数进行填充。
噪音数据的处理方法(使用3sigma原则或者箱线图发现离群点,再进行删除操作):
1、正态分布的3sigma原则

2、箱线图进行监测,发现离群数据,进一步删除离群点(箱线图又称为五分位图)其中含有离群点、最大值、最小值、四分之一位数、四分之三位数、中位数。
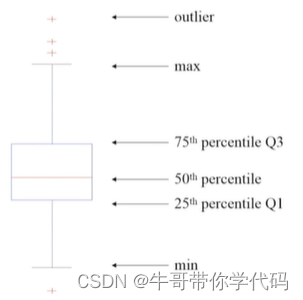
上述图中的最小值和最大值不一定会指的是数据中的真正的最小值和最大值,因为数据中真正的最小值和最大值可能是离群点。怎样求最小值和最大值捏?使用下面公式进行判断:
我们计四分之一位数为Q1,四分之三位数为Q3。
首先计算四分之一极差:
四分之一极差 IQR=Q3-Q1
最大值=Q3+1.5*极差
最小值=Q1-1.5*极差
离群点:通常情况下的一个值高于1.5倍的极差或者低于1.5倍的极差。.
使用下面代码即可绘制箱线图
import pandas as pd
import numpy as np
import matplotlib.pyplot as pl
from sklearn.impute import Simplelmputer
data url = "train.csv"
df= pd.read_csv(data_url)
imp = SimpleImputer(missing_values = np.nan, strategy = 'mean')
imp.fit(df.iloc[:,5:6))
pl.boxplot(imp.transform(df.iloc[:,5:6])
pl.xlabel('data')
pl.show()
数据转换
数据中既有字符串也有数值、且数值量纲不统一。
需要统一化:字符数值统一化
需要规范化:统一量纲
离散数据特征的二进制编码
对于标称类(无序)离散数据连续化特征构造通常采用二进制编码方法
对于序数类离散数据连续化特征构造可以直接使用[0,m-1]的整数
数据规范化
最小最大规范化: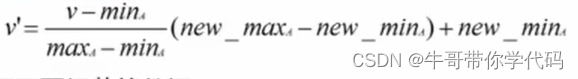
z-分数规范化:

小数定标:移动属性A的小数点位置(移动位数依赖于属性A的最大值)v'=v/10^j , j为使Max(|v'|)<1的最小整数
二进制编码方式
(1)代码实现sklearn中的OneHotEncoder(独热编码)->二进制中只允许一位为1
import pandas as pd
from sklearn import preprocessing
data_url = "train.csv"
df= pd.read_esv(data_url)
X = df.iloc[:,4:5]
enc = preprocessing.OneHotEncoder()
y = enc.fit_transform(X).toarray()
print(y) 
上述代码是将序数类型的数据编码成[0,m-1]范围内的整数
哑编码(允许多个位为一)
哑编码需要更少的二进制编码,独热编码需要更多的二进制编码(因为独热编码只允许一个二进制为1,所以没有哑编码的表现力那么强,需要更多的二进制编码)。
import pandas as pd
data_url = "train.csv"
df = pd.read_csv(data_url)
X = df.iloc[:,11:12]
y = pd.get_dummies(X,drop_first=True)
print(y)drop_first=True 为哑编码
drop_first=False 为独热编码
上面的代码既可以做独热编码也可以做哑编码
两种规范化函数
最小最大规范化函数
from sklearn import preprocessing
data_url = "train.csv"
df= pd.read_csv(data_url)
imp = Simplelmputer(missing_values = np.nan, strategy = 'mean')
imp.fit(df.iloc[:,5:6])
X = imp.transform(df.iloc[:,5:6])
min_max_scaler = preprocessing.MinMaxScaler()
X_train_minmax = min_max_scaler.fit_transform(X)
print(X_train_minmax)当获得的数据属于数值类型数据时,可以在建模之前使用最小最大规范化函数对量纲作一个统一。同时,我们也可以使用下面的方法进行量纲的统一。
z得分规范化
import pandas as pd
import numpy as np
from sklearn.impute import Simplelmputer
from sklearn import preprocessing
data_url = "train.csv"
df= pd.read_csv(data_url)
imp = Simplelmputer(missing_values = np.nan, strategy = 'mean')
imp.fit(df.iloc[:,5:6])
X = imp.transform(df.iloc[:,5:6])
scaler = preprocessing.scale(X)
print(scaler)数据降维
散点图分析(如何绘制散点图)
用来显示两组数据的相关性分布
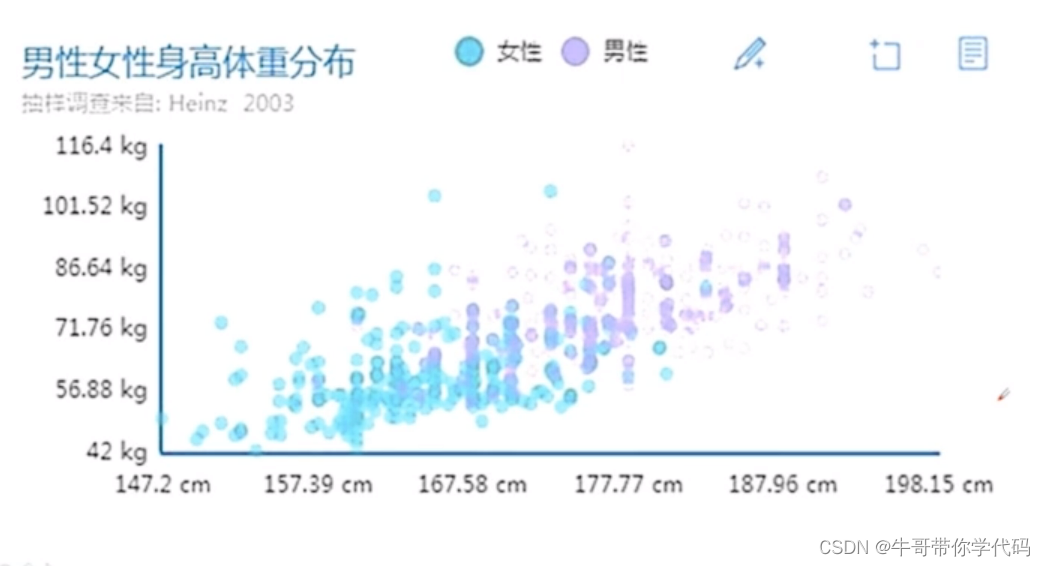
PCA(主成分分析)
直观理解(坐标轴的旋转)

在普通的XY轴坐标系,我们对每个点求方差,会发现方差比较大,也就意味着在X、Y轴上的信息量都比较大。因此不管舍弃哪一维都会损失数据的信息量。
通过PCA旋转,我们可以看到下面的图片,在长轴上数据的方差依然非常大,但是在短轴上方差非常小。方差小说明信息量就比较小。在这时,假如我们保留长轴数据,去掉短轴数据,对数据量的丢失也不会出现很明显的现象。
总的来说,PCA分析法就是通过坐标轴的旋转,将每个坐标轴信息量比较大的数据,经过旋转,使得在长轴上的信息量比较大。短轴上的信息量比较小。(实现了一种线性变换)
最终得到的结果形如
Z1=0.78*x1+0.01*x2+0.56*x3+0.067*x4
Z2=0.086*x1+0.76*x2+0.45*x3+0.97*x4
上面的主成分Z1、Z2分别由原来的四维数据(四种变量)降维得到。我们可以看到对于上面的二维数据我们可以看出来每种主成分中对应的变量的权值系数的不同。
权值系数的求解过程(了解即可):
对数据的相关矩阵求特征值特征向量,最后得到相应的权值
from sklearn.decomposition import PCA
import pandas as pd
data_url = "iris_train.csv"
df= pd.read_csv(data_url)
X = df.iloc[:,1:5]
y=df.iloc[:,5]
pca = PCA(n_components=4)
pca.fit(X)
print(pca.explained_variance_ratio_)绘制相关性矩阵图片(热力图)
使用热力图可以对相关性进行更清晰的描述和直观理解
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
train csv ='trainOX.csv'
train data = pdread csv(train_csv)
train data.drop(['ID','date','hour'],axis=1,inplace=True)
corrmat = train_data.corr()
f;ax = plt.subplots(figsize=(12,8))
sns.heatmap(corrmat, vmax=0.8, square=True)
plt.show()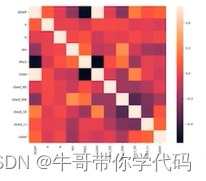
准确率评价
混淆矩阵
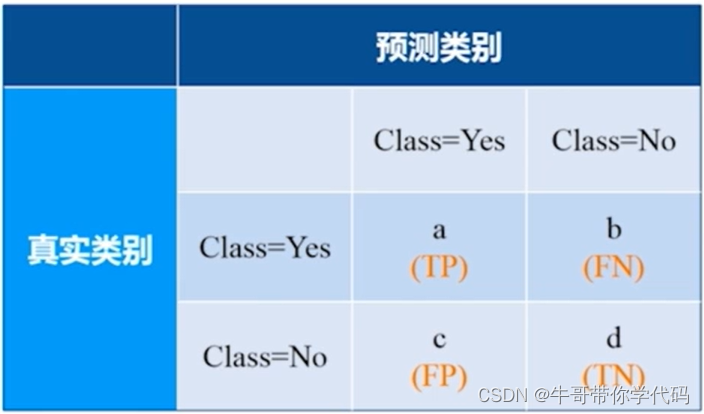
对于准确率的评价可以使用混淆矩阵的方法进行评估
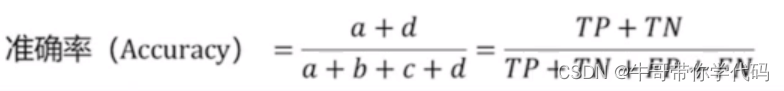
上述公式是准确率的计算公式
对应的左侧对应一列为样本中数据的真实类别。上边一行对应的是样本中数据的预测数据。
a对应的又称为真阳例(True Positive)、b对应的又称为假阴例(False Negative)、c对应的又称为假阳例(False Negative)、d对应的为真阴例(True Negative)。
对于各个类别的相关解释:
真阳例:指的是实际数据与预测数据结果相同的情况,数据本身为正类,我们把它预测为正类。(比如一部分用户是生病的,我们将其也预测为生病的,这样的用户数目即为真阳例)
假阴例:一个用户是生病的,但是通过模型预测的结果是没有生病的。
假阳例:本身是一个没有生病的客户,但是通过模型进行预测的结果为一个生病的客户,故为假阳例。
真阴例:客户没有生病,使用模型进行预测也没有生病。
显而易见上述混淆矩阵中,TP与TN是预测正确的(本身是正确的和本身不是正确的都预测准确了)。
对于数据检验部分,我们往往会将数据七三分为训练集和测试集两部分。
除此之外,我们往往也会使用K折交叉验证的方法对数据进行相关的验证。
K折交叉验证
在数据检验时,使用数据集中的倒数第k份数据进行检验,例如,第一次,使用倒数第1份数据进行检验;第二次检验,使用倒数第2份数据进行检验;第三次,使用倒数第3份数据进行检验....最多进行十折交叉验证。
知识点补充:
K-Means算法
优点
-
聚类时间快
-
当结果簇是密集的,而簇与簇之间区别明显时,效果较好
-
相对可扩展和有效,能对大数据集进行高效划分
缺点
-
用户必须事先指定聚类簇的个数
-
常常终止于局部最优
-
只适用于数值属性聚类(计算均值有意义)
-
对噪声和异常数据也很敏感
-
不同的初始值,结果可能不同
-
不适合发现非凸面形状的簇
相关文章:
数据挖掘全流程解析
数据挖掘全流程解析 数据指标选择 在这一阶段,使用直方图和柱状图的方式对数据进行分析,观察什么数据属性对于因变量会产生更加明显的结果。 如何绘制直方图和条形统计图 数据清洗 观察数据是否存在数据缺失或者离群点的情况。 数据异常的两种情况…...

详细介绍如何对音乐信息进行检索和音频节拍跟踪
在本文中,我们将了解节拍的概念,以及我们在尝试跟踪节拍时面临的挑战。然后我们将介绍解决问题的方法以及业界最先进的解决方案。 介绍 音乐就在我们身边。每当我们听到任何与我们的心灵和思想相关的音乐时,我们就会迷失其中。我们下意识地随着听到的节拍而敲击。您一定已…...
Java课题笔记~ HTTP协议(请求和响应)
Servlet最主要的作用就是处理客户端请求,并向客户端做出响应。为此,针对Servlet的每次请求,Web服务器在调用service()方法之前,都会创建两个对象 分别是HttpServletRequest和HttpServletResponse。 其中HttpServletRequest用于封…...

在x86下运行的Ubuntu系统上部署QEMU用于模拟RISC-V硬件环境
1.配置工作环境 sudo apt install gcc bison flex libncurses-dev ninja-build \pkg-config build-essential zlib1g-dev pkg-config libglib2.0-dev \binutils-dev libboost-all-dev autoconf libtool libssl-dev \libpixman-1-dev python-capstone virtualenv software-prop…...

网络爬虫选择代理IP的标准
Hey,小伙伴们!作为一家http代理产品供应商,我知道网络爬虫在选择代理IP时可能会遇到些问题,毕竟市面上有很多选择。别担心!今天我要给大家分享一些实用的建议,帮助你们选择适合网络爬虫的代理IP。一起来看看…...

RxJava 复刻简版之三,map 多次中转数据
案例代码:https://gitee.com/bobidali/lite-rx-java/commit/292e9227a5491f7ec6a07f395292ef8e6ff69290 RxJava 的调用第一步是封装了观察者接受了数据的处理,进一步就是使用 map 将数据操作传递给上下游 1、类似Observer.create 创建一个简单的观察者…...
)
06 Word2Vec模型(第一个专门做词向量的模型,CBOW和Skip-gram)
博客配套视频链接: https://space.bilibili.com/383551518?spm_id_from=333.1007.0.0 b 站直接看 配套 github 链接:https://github.com/nickchen121/Pre-training-language-model 配套博客链接:https://www.cnblogs.com/nickchen121/p/15105048.html 神经网络语言模型(NNL…...
Axure RP9小白安装教程
第一步: 打开:Axure中文学习网 第二步: 鼠标移动软件下载,点击Axure RP 9下载既可 第三步: 注意:Axure RP 9 MAC正式版为苹果版本,Axure RP 9 WIN正式版为Windows版本 中文汉化包ÿ…...

腾讯云CVM服务器2核2g1m带宽支持多少人访问?
腾讯云2核2g1m的服务器支持多少人同时访问?2核2g1m云服务器短板是在1M公网带宽上,腾讯云服务器网以网站应用为例,当大规模用户同时访问网站时,很大概率会卡在公网带宽上,所以压根就谈不上2核2G的CPU内存计算性能是否够…...

8.12学习笔记
在PyTorch中,Dataset和DataLoader是用于处理数据的两个重要类。Dataset类是一个抽象类,用于表示数据集。它的主要作用是将数据加载到内存中,并提供一种统一的方式来访问数据。为了使用Dataset类,你需要继承它并实现两个方法&#…...

计算机体系中的不同的缓存存储层级说明
分级说明 L1缓存的标准延迟是4个周期。这意味着,当CPU请求数据时,L1缓存需要4个时钟周期来将数据传输给CPU。 L2缓存的标准延迟是12个周期。相对于L1缓存,L2缓存的容量更大,但其读取速度更慢,需要更多的时钟周期来传输…...
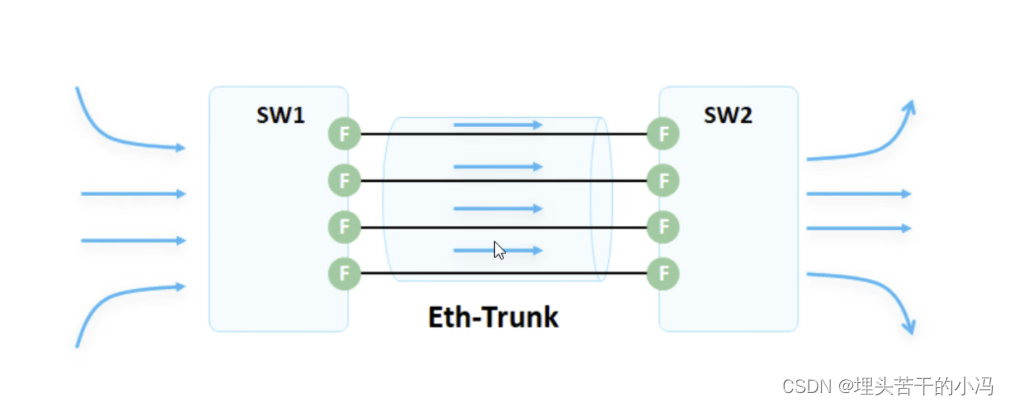
HCIP 链路聚合技术
1、链路聚合概述 为了保证网络的稳定性,仅仅是设备进行备份还不够,我们需要针对我们的链路进行备份,同时也增加了链路的利用率,提高带宽。避免一条链路出现故障,导致网络无法正常通信。这就可以使用链路聚合技术。 以…...

网页爬虫中常用代理IP主要有哪几种?
各位爬虫探索者,你是否有想过在网页爬虫中使用代理IP来规避限制实现数据自由?在这篇文章中,作为一名IP代理产品供应商,我将为你揭示常见的网页爬虫代理IP类型,让你在爬虫的世界中游刃有余! 一、免费公开代理…...
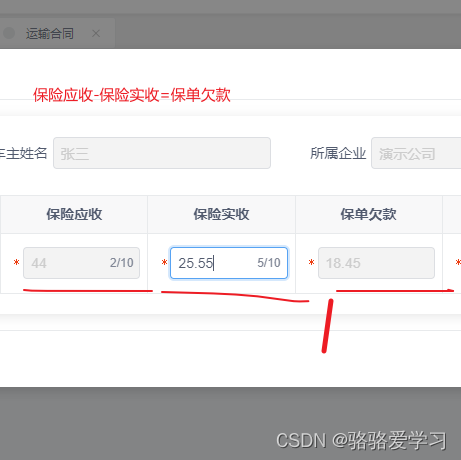
Js小数运算精度缺失的解决方法
项目场景: 提示:项目需求截图: 问题描述 众所周知Js做运算时0.10.2不等于0.3,目前项目需要计算关于金额的选项,涉及到金额保留后两位。保单欠款是根据用户输入的保单应收和保单欠款自动计算的。 原因分析: 产生浮点数…...

25 | 葡萄酒质量数据分析
基于kaggle提供的公开数据集,对全球葡萄酒分布情况和质量情况进行数据探索和分析 from kaggle: https://www.kaggle.com/zynicide/wine-reviews 分析思路: 0、数据准备 1、葡萄酒的种类 2、葡萄酒质量 3、葡萄酒价格 4、葡萄酒描述词库 5、品鉴师信息 6、总结 0、数据准备 …...
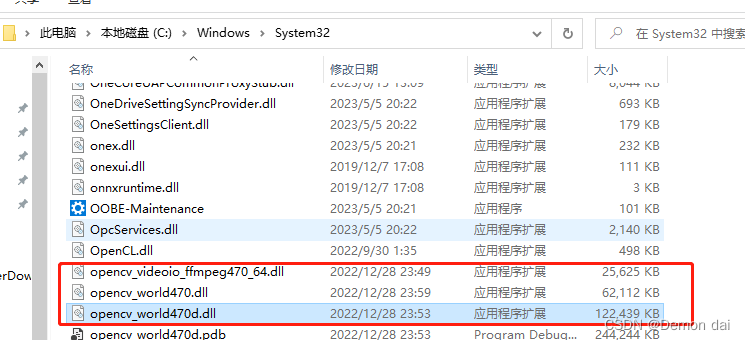
在 Windows 上安装 OpenCV – C++ / Python
在这篇博文中,我们将在 Windows 上安装适用于 C 和 Python 的 OpenCV。 C 安装是在自定义安装 exe 文件的帮助下完成的。而Python的安装是通过Anaconda完成的。 在 Windows 上安装 OpenCV – C / Python(opencv官方Wndows上安装openCV- C/ Pthon 的链接…...

前后端交互开发模式yapi使用
接手一个项目组,采用前后端开发模式分离,经过一阵子了解后,发现存在前后端配合不顺畅的情况,存在如下两个问题, 一:没有接口协议,前端开发时先用占位符,等后端开发协议出来后替换,影响效率。 二:前端开发好了, 后端没开发好,前端只能等待后端开发好。 做为一个团队技…...
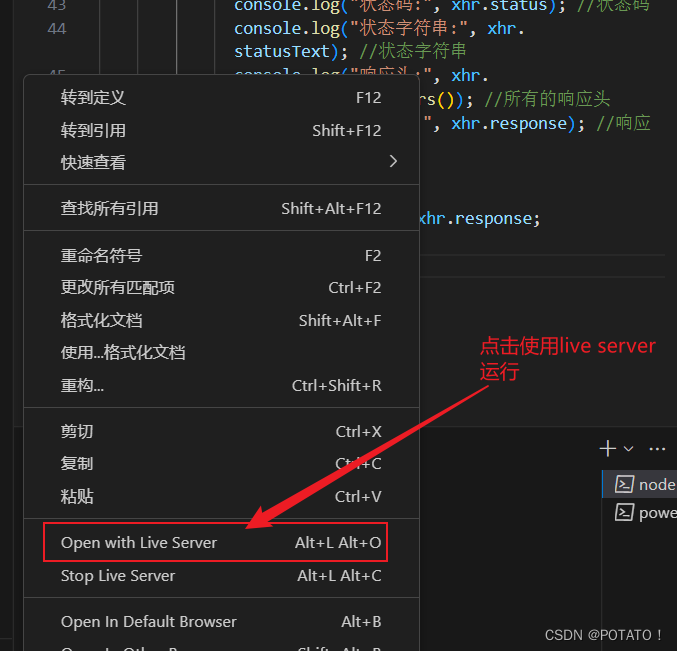
Ajax同源策略及跨域问题
Ajax同源策略及跨域问题 同源策略ajax跨域问题什么是跨域?为什么不允许跨域?跨域解决方案1、CORS2、express自带的中间件cors3、JSONP原生JSONPjQuery发送JSONP 4、使用vscode的Live Server插件 同源策略 同源策略(Same-Origin Policy&#…...

JavaScript:解构赋值【对象】
在JavaScript编程中,解构赋值是一种强大的技术,它允许我们从数组或对象中快速提取数据并赋值给变量。在本文中,我们将重点介绍对象解构,解释如何利用它从对象中提取数据,以通俗易懂的方式帮助你掌握这一技巧。 1. 什么…...
微服务与Nacos概述-2
微服务间消息传递 微服务是一种软件开发架构,它将一个大型应用程序拆分为一系列小型、独立的服务。每个服务都可以独立开发、部署和扩展,并通过轻量级的通信机制进行交互。 应用开发 common模块中包含服务提供者和服务消费者共享的内容 provider模块是…...

【OSG学习笔记】Day 18: 碰撞检测与物理交互
物理引擎(Physics Engine) 物理引擎 是一种通过计算机模拟物理规律(如力学、碰撞、重力、流体动力学等)的软件工具或库。 它的核心目标是在虚拟环境中逼真地模拟物体的运动和交互,广泛应用于 游戏开发、动画制作、虚…...
)
React Native 开发环境搭建(全平台详解)
React Native 开发环境搭建(全平台详解) 在开始使用 React Native 开发移动应用之前,正确设置开发环境是至关重要的一步。本文将为你提供一份全面的指南,涵盖 macOS 和 Windows 平台的配置步骤,如何在 Android 和 iOS…...

如何在看板中体现优先级变化
在看板中有效体现优先级变化的关键措施包括:采用颜色或标签标识优先级、设置任务排序规则、使用独立的优先级列或泳道、结合自动化规则同步优先级变化、建立定期的优先级审查流程。其中,设置任务排序规则尤其重要,因为它让看板视觉上直观地体…...

OkHttp 中实现断点续传 demo
在 OkHttp 中实现断点续传主要通过以下步骤完成,核心是利用 HTTP 协议的 Range 请求头指定下载范围: 实现原理 Range 请求头:向服务器请求文件的特定字节范围(如 Range: bytes1024-) 本地文件记录:保存已…...

数据链路层的主要功能是什么
数据链路层(OSI模型第2层)的核心功能是在相邻网络节点(如交换机、主机)间提供可靠的数据帧传输服务,主要职责包括: 🔑 核心功能详解: 帧封装与解封装 封装: 将网络层下发…...

Mac软件卸载指南,简单易懂!
刚和Adobe分手,它却总在Library里给你写"回忆录"?卸载的Final Cut Pro像电子幽灵般阴魂不散?总是会有残留文件,别慌!这份Mac软件卸载指南,将用最硬核的方式教你"数字分手术"࿰…...

学习STC51单片机32(芯片为STC89C52RCRC)OLED显示屏2
每日一言 今天的每一份坚持,都是在为未来积攒底气。 案例:OLED显示一个A 这边观察到一个点,怎么雪花了就是都是乱七八糟的占满了屏幕。。 解释 : 如果代码里信号切换太快(比如 SDA 刚变,SCL 立刻变&#…...
安装docker)
Linux离线(zip方式)安装docker
目录 基础信息操作系统信息docker信息 安装实例安装步骤示例 遇到的问题问题1:修改默认工作路径启动失败问题2 找不到对应组 基础信息 操作系统信息 OS版本:CentOS 7 64位 内核版本:3.10.0 相关命令: uname -rcat /etc/os-rele…...

浪潮交换机配置track检测实现高速公路收费网络主备切换NQA
浪潮交换机track配置 项目背景高速网络拓扑网络情况分析通信线路收费网络路由 收费汇聚交换机相应配置收费汇聚track配置 项目背景 在实施省内一条高速公路时遇到的需求,本次涉及的主要是收费汇聚交换机的配置,浪潮网络设备在高速项目很少,通…...

【Android】Android 开发 ADB 常用指令
查看当前连接的设备 adb devices 连接设备 adb connect 设备IP 断开已连接的设备 adb disconnect 设备IP 安装应用 adb install 安装包的路径 卸载应用 adb uninstall 应用包名 查看已安装的应用包名 adb shell pm list packages 查看已安装的第三方应用包名 adb shell pm list…...
