2023牛客暑期多校训练营7
Beautiful Sequence 贪心,二进制,构造
Cyperation 模拟 ,数学
We Love Strings 分块,二进制枚举,二进制容斥dp
Writing Books 签到

根据相邻两个异或值B,因为前小于等于后,故从高到低遍历B的每一位时,第一个是1的位置,一定决定了前者与后者的大小关系。且前者这一位必定是0,后者这一位必定是1。有根据B的前缀异或和是A1^Ai,如果A1^Ai这一位是0,那么A1这一位必定填1,否则必定填0。
这样处理之后,A1会形成若干确定的填法。而对于剩余没能确定的,也就是字典序产生的由来。继续从高到低遍历每一位,当前位置i若没有确定,如果位置i之前(所有小于位置i)的有x的没有确定的,那么当前填0的贡献为(1<<x),这一贡献如果大于等于k,这一位就必定是0,否则,这一位必定是1。
#include<bits/stdc++.h>
using namespace std;
typedef long long int ll;
const int N=1e6+5;
long long n,k,b[N],T,c[N],d[50];
ll qp(ll base,ll pow)
{ll ans=1;while(pow){if(pow&1)ans=ans*base;pow>>=1;base=base*base;}return ans;
}
int main()
{cin>>T;while(T--){cin>>n>>k;int f=1;for(int i=1; i<n; i++)cin>>b[i],c[i]=c[i-1]^b[i];int t=0;memset(d,-1,sizeof(d));for(int i=1; i<n&&f; i++){for(int j=29; j>=0; j--){if(b[i]>>j) {if(d[j]!=-1&&d[j]!=1^((c[i]>>j)&1)){f=0;break;}d[j]=1^((c[i]>>j)&1);break;}}}int pre[50];memset(pre,0,sizeof(pre));pre[0]=(d[0]==-1);for(int i=1; i<=29; i++){pre[i]=pre[i-1];if(d[i]==-1)pre[i]++;}for(int i=29; i>=1; i--){if(d[i]==-1){ll temp=qp(2ll,pre[i-1]);if(k<=temp){d[i]=0;}else{d[i]=1;k-=(temp);}}}if(d[0]==-1){if(k==1){d[0]=0;}else if(k==2){d[0]=1;k=1;}}if(k>1||f==0)puts("-1");else{int p=0;for(int i=29; i>=0; i--){p=p<<1|d[i];}for(int i=0; i<n; i++){printf("%d ",(p^c[i]));}puts("");}}
}

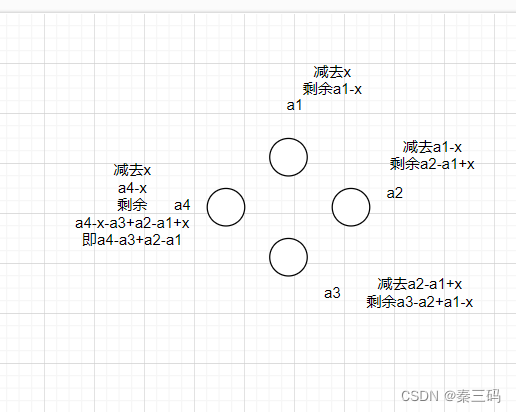
首先一个大环可以拆成若干互不影响的小环。先拆环为链,即设a1和ak共同减去了x,则接下来的删除,是固定方向的,由a1开始到ak结束。上图为偶数情况,一个合法的x,要满足每一轮相减的剩余量都大于等于0,最后的a4剩余量为0.这一过程,维护x的取值范围,判断合法即可。
对于奇数同理,只是多了一个判断剩余量是否能够整除2,和整除解出来的x是否合法。
#include<bits/stdc++.h>
using namespace std;
typedef long long int ll;
int vis[1000000+10],a[1000000+10];
int main()
{cin.tie(0);ios::sync_with_stdio(0);int t;cin>>t;while(t--){int n,k;cin>>n>>k;int zero=0;for(int i=1; i<=n; i++){cin>>a[i];if(a[i])zero=1;vis[i]=0;}if(k>n/2){if(zero){cout<<"NO"<<'\n';}elsecout<<"YES"<<'\n';continue;}int flag=1;for(int i=1; i<=n; i++){if(vis[i])continue;int now=i;ll temp=0;int op=1;ll L=-1e18,R=1e18;//cout<<" ===== "<<endl;while(!vis[now]){vis[now]=1;// cout<<now<<" ";if(op==1){R=min(R,a[now]-temp);}else{L=max(L,temp-a[now]);}op^=1;temp=a[now]-temp;now+=k;now%=n;if(now==0)now=n;}if(L>R){flag=0;break;}if(op==1){if(temp==0)continue;flag=0;}if(op==0){if(temp%2){flag=0;continue;}temp/=2;if(temp<L||temp>R){flag=0;continue;}}}if(flag==0){cout<<"NO"<<'\n';}else{cout<<"YES"<<'\n';}}return 0;
}
这题可以分块做,400给的很巧妙,这就意味这长度小于20的,可以暴力枚举,长度大于20的,不会超过20个,仍然可以暴力枚举。
对于前者,相同长度的可以暴力枚举每一位01情况,然后进行检查,一旦检查出可以的,就答案++
对于后者,也是相同长度的暴力枚举,但枚举方式变为,这x个字符串哪个参与匹配,哪个不参与。对于一个枚举出的方案,若合法(已知位置不冲突),则这一方案的方案数为其不确定位置的个数的2次幂。但直接统计肯定会有重复。因为如2 3 4组成的集合方案数,就包含了2 3 4 5的方案数。这种重复出现在,2 3 4组成集合的问号区域,乘了2,这个2就包含了2 3 4 5的部分。故需要从2 3 4方案数里面减去。按照二进制容斥原理来说,就是满足小集合的方案数里面包含了满足大集合的,需要从小集合里面容斥掉大集合的。
#include <bits/stdc++.h>
using namespace std;
typedef long long int ll;
vector<string>v[410];
int n;
ll ans;
# define mod 998244353
void workxiao(int len)
{if(v[len].size()==0)return ;for(int i=0;i<(1<<len);i++){for(auto it:v[len]){int flag=0;for(int j=0;j<len;j++){if((i&(1<<j))){if(it[j]=='0')flag=1;}else{if(it[j]=='1')flag=1;}}if(flag==0){ans++;ans%=mod;break;}}}
}
ll dp[(1<<22)],pre[410];
void init()
{pre[0]=1;for(int i=1;i<=400;i++){pre[i]=pre[i-1]*2ll%mod;}
}
int check(string now)
{int ans=0;for(int i=0;i<now.length();i++){ans+=(now[i]=='?');}return ans;
}
void workda(int len)
{if(v[len].size()==0)return ;int nown=v[len].size();string temp="";for(int i=0;i<len;i++){temp+='?';}for(int i=1;i<(1<<nown);i++){dp[i]=0;string now=temp;int flag=0;for(int j=0;j<nown;j++){if((i&(1<<j))){for(int k=0;k<len;k++){if(v[len][j][k]!='?'){if(now[k]=='?'){now[k]=v[len][j][k];}else{if(now[k]!=v[len][j][k]){flag=1;break;}}}}}if(flag)break;}if(flag==0)dp[i]=pre[check(now)];}for(int i=1;i<(1<<nown);i++){for(int j=0;j<nown;j++){if((i&(1<<j))){dp[(i^(1<<j))]=((dp[(i^(1<<j))]-dp[i])%mod+mod)%mod;}}}for(int i=1;i<(1<<nown);i++){ans+=dp[i];ans%=mod;}}
int main()
{init();cin>>n;for(int i=1;i<=n;i++){string s;cin>>s;v[(int)(s.length())].push_back(s);}for(int i=1;i<=20;i++){workxiao(i);}for(int i=21;i<=400;i++){workda(i);}cout<<ans;return 0;
}
签到题,不赘述
相关文章:

2023牛客暑期多校训练营7
Beautiful Sequence 贪心,二进制,构造 Cyperation 模拟 ,数学 We Love Strings 分块,二进制枚举,二进制容斥dp Writing Books 签到 根据相邻两个异或值B,因为前小于等于后,故从高到低遍历B的每一…...
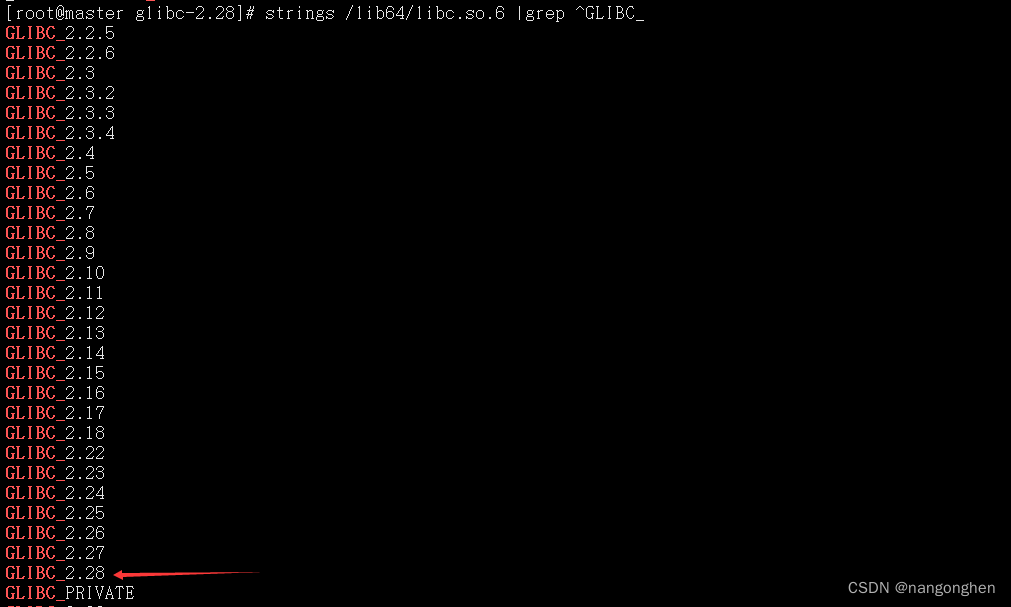
centos7升级glibc2.28
1 概述 centos7自带的glibc对于某些软件是太旧的,决定将glibc升级至2.28。 2 安装过程 2.1 下载glibc源码 mkdir -p /opt/third-party && cd /opt/third-party wget http://ftp.gnu.org/gnu/glibc/glibc-2.28.tar.gz tar -xf glibc-2.28.tar.gz cd glibc…...
腾讯云香港服务器租用_2核2G20M_2核4G30M
腾讯云香港服务器租用费用表,目前中国香港地域轻量应用服务器可选配置2核2G20M、2核2G30M、2核4G30M,操作系统可选Windows和Linux,不只是香港云服务器,新加坡、硅谷、法兰克福和东京服务器均有活动,腾讯云服务器网分享…...

十三、ESP32PS2摇杆(ADC)
1. 运行效果 在上下左右操作PS2摇杆的时候,会检测到数据 2. 滑动电阻...
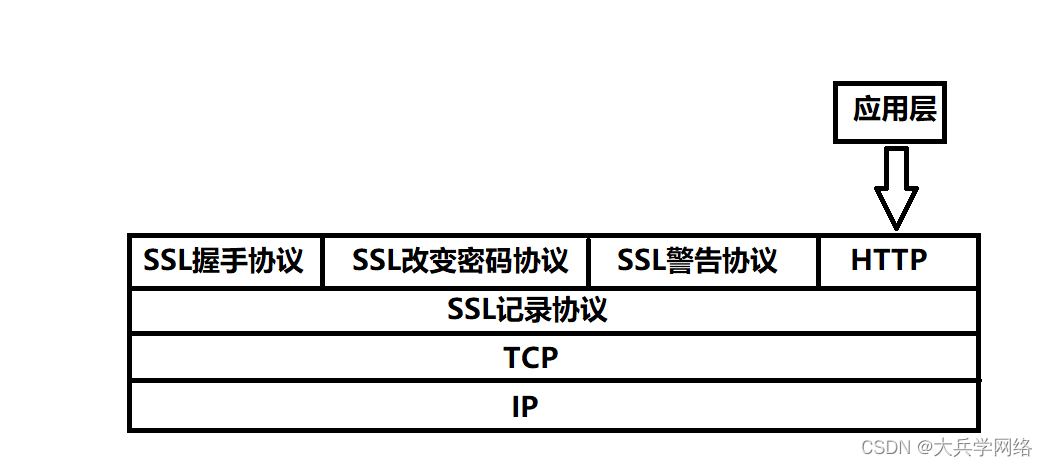
网络安全的相关知识点
网络安全威胁类型: 1.窃听:广播式网络系统。 2.假冒 3.重放:重复一份报文或者报文的一部分,以便产生一个被授权的效果。 4.流量分析 5.数据完整性破坏 6.拒绝服务 7.资源的非授权使用 8.陷门和特洛伊木马:木马病毒有客…...
:牛客在线编程06 递归/回溯)
算法练习(6):牛客在线编程06 递归/回溯
package jz.bm;import java.io.PushbackInputStream; import java.lang.reflect.Array; import java.util.ArrayList; import java.util.Arrays;public class bm6 {/*** BM55 没有重复项数字的全排列*/ArrayList<ArrayList<Integer>> res new ArrayList<>()…...
图像局部二值化处理实例)
C#使用OpenCv(OpenCVSharp)图像局部二值化处理实例
本文实例演示C#语言中如何使用OpenCv(OpenCVSharp)对图像进行局部二值化处理。 目录 图像二值化原理 局部二值化 自适应阈值 实例 效果...

MySQL多表关联查询
目录 1. inner join: 2. left join: 3. right join: 4.自连接 5.交叉连接: 6、联合查询 7、子查询 1. inner join: 代表选择的是两个表的交差部分。 内连接就是表间的主键与外键相连,只取得键值一致…...

flutter开发实战-CustomClipper裁剪长图帧动画效果
flutter开发实战-CustomClipper裁剪长图帧动画效果 在开发过程中,经常遇到帧动画的每一帧图显示在超长图上,需要处理这种帧动画效果。我这里使用的是CustomClipper 一、CustomClipper CustomClipper继承于Listenable abstract class CustomClipper e…...

CSS 中的优先级规则是怎样的?
聚沙成塔每天进步一点点 ⭐ 专栏简介⭐内联样式(Inline Styles)⭐ID 选择器(ID Selectors)⭐类选择器、属性选择器和伪类选择器(Class, Attribute, and Pseudo-class Selectors)⭐元素选择器和伪元素选择器…...

概率图模型(Probabilistic Graphical Model,PGM)
概率图模型(Probabilistic Graphical Model,PGM),是一种用图结构来描述多元随机变量之间条件独立性的概率模型。它可以用来表示复杂的概率分布,进行有效的推理和学习,以及解决各种实际问题,如图…...

Oracle 知识篇+会话级全局临时表在不同连接模式中的表现
标签:会话级临时表、全局临时表、幻读释义:Oracle 全局临时表又叫GTT ★ 结论 ✔ 专用服务器模式:不同应用会话只能访问自己的数据 ✔ 共享服务器模式:不同应用会话只能访问自己的数据 ✔ 数据库驻留连接池模式:不同应…...
MySQL 数据库文件的导入导出
目录 数据库的导出 导出整个数据库 导出数据库中的数据表 导出数据库结构 导出数据库中表的表结构 导出多个数据库 导出所有数据库 数据库的导入 数据库的导出 mysqldump -h IP地址 -P 端口 -u 用户名 -p 数据库名 > 导出的文件名 用管理员权限打开cmd进入MySQL的bi…...
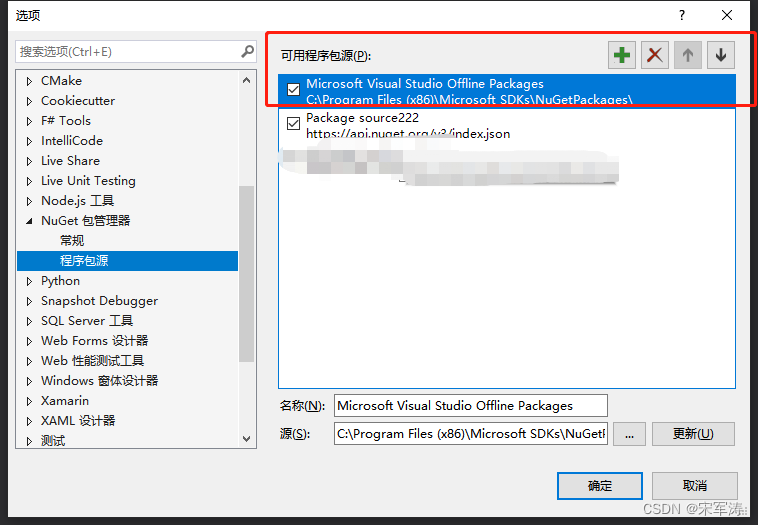
找不到资产文件project.assets.json
NuGet 在“obj”文件夹中写入名为 project.assets.json 的文件,.NET SDK 使用该文件来获取有关要传递到编译器的包的信息 。 如果在生成过程中找不到资产文件 project.assets.json,则会发生此错误。 1.执行命令的方式解决 点击工具,分别展开命…...
【python】python将json字符串导出excel | pandas处理json字符串保存为csv
如何将json转为csv 1、通过json直接转为csv 在Python中,你可以使用pandas库来处理DataFrame(数据帧)和将JSON数据转换为CSV格式。下面是一个简单的示例代码,展示了如何使用pandas库将JSON数据转换为CSV文件: import p…...

opencv 基础54-利用形状场景算法比较轮廓-cv2.createShapeContextDistanceExtractor()
注意:新版本的opencv 4 已经没有这个函数 cv2.createShapeContextDistanceExtractor() 形状场景算法是一种用于比较轮廓或形状的方法。这种算法通常用于计算两个形状之间的相似性或差异性,以及找到最佳的匹配方式。 下面是一种基本的比较轮廓的流程&…...

分布式系统理论
以前的架构...

Gartner发布2023年的存储技术成熟曲线
技术路线说明 Gartner自1995年起开始采用技术成熟度曲线,它描述创新的典型发展过程,即从过热期发展到幻灭低谷期,再到人们最终理解创新在市场或领域内的意义和角色。 一项技术 (或相关创新)在发展到最终成熟期的过程中经历多个阶段࿱…...
c++ 有元
友元分为两部分内容 友元函数友元类 友元函数 问题:当我们尝试去重载operator<<,然后发现没办法将operator<<重载成成员函数。因为cout的输出流对象和隐含的this指针在抢占第一个参数的位置。this指针默认是第一个参数也就是左操作 数了。…...
安卓:网络框架okhttp
目录 一、okhttp介绍 1. OkHttpClient类: 常用方法: 2. Request类: 常用方法: 3. Response类: 常用方法: 4. Call类: 常用方法: 5. Interceptor接口: 常用方法&…...

测试微信模版消息推送
进入“开发接口管理”--“公众平台测试账号”,无需申请公众账号、可在测试账号中体验并测试微信公众平台所有高级接口。 获取access_token: 自定义模版消息: 关注测试号:扫二维码关注测试号。 发送模版消息: import requests da…...

Cesium1.95中高性能加载1500个点
一、基本方式: 图标使用.png比.svg性能要好 <template><div id"cesiumContainer"></div><div class"toolbar"><button id"resetButton">重新生成点</button><span id"countDisplay&qu…...

YSYX学习记录(八)
C语言,练习0: 先创建一个文件夹,我用的是物理机: 安装build-essential 练习1: 我注释掉了 #include <stdio.h> 出现下面错误 在你的文本编辑器中打开ex1文件,随机修改或删除一部分,之后…...

【android bluetooth 框架分析 04】【bt-framework 层详解 1】【BluetoothProperties介绍】
1. BluetoothProperties介绍 libsysprop/srcs/android/sysprop/BluetoothProperties.sysprop BluetoothProperties.sysprop 是 Android AOSP 中的一种 系统属性定义文件(System Property Definition File),用于声明和管理 Bluetooth 模块相…...

Mac软件卸载指南,简单易懂!
刚和Adobe分手,它却总在Library里给你写"回忆录"?卸载的Final Cut Pro像电子幽灵般阴魂不散?总是会有残留文件,别慌!这份Mac软件卸载指南,将用最硬核的方式教你"数字分手术"࿰…...

ElasticSearch搜索引擎之倒排索引及其底层算法
文章目录 一、搜索引擎1、什么是搜索引擎?2、搜索引擎的分类3、常用的搜索引擎4、搜索引擎的特点二、倒排索引1、简介2、为什么倒排索引不用B+树1.创建时间长,文件大。2.其次,树深,IO次数可怕。3.索引可能会失效。4.精准度差。三. 倒排索引四、算法1、Term Index的算法2、 …...

select、poll、epoll 与 Reactor 模式
在高并发网络编程领域,高效处理大量连接和 I/O 事件是系统性能的关键。select、poll、epoll 作为 I/O 多路复用技术的代表,以及基于它们实现的 Reactor 模式,为开发者提供了强大的工具。本文将深入探讨这些技术的底层原理、优缺点。 一、I…...

AspectJ 在 Android 中的完整使用指南
一、环境配置(Gradle 7.0 适配) 1. 项目级 build.gradle // 注意:沪江插件已停更,推荐官方兼容方案 buildscript {dependencies {classpath org.aspectj:aspectjtools:1.9.9.1 // AspectJ 工具} } 2. 模块级 build.gradle plu…...

Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信
文章目录 Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信前言一、网络通信基础概念二、服务端与客户端的完整流程图解三、每一步的详细讲解和代码示例1. 创建Socket(服务端和客户端都要)2. 绑定本地地址和端口&#x…...

在 Spring Boot 项目里,MYSQL中json类型字段使用
前言: 因为程序特殊需求导致,需要mysql数据库存储json类型数据,因此记录一下使用流程 1.java实体中新增字段 private List<User> users 2.增加mybatis-plus注解 TableField(typeHandler FastjsonTypeHandler.class) private Lis…...
