【笔记】树状数组

【笔记】树状数组 目录
- 简介
- 引入
- 1. 直接暴力
- 2. 维护前缀和数组
- 总结
- 定义
- 前置知识: lowbit \operatorname{lowbit} lowbit 操作
- 区间的表示方法
- 操作
- 单点修改
- 前缀和查询
- 任意区间查询
- 例题1: 单点修改,区间查询
- 例题2: 区间修改,单点查询
- 例题3: 区间修改,区间查询
- (后附极限卡常代码,70ms,较优解)
简介
树状数组是一种树形数据结构,支持在 O ( log n ) O(\log n) O(logn) 的时间复杂度内进行 单点修改 和 查询前缀和 的操作。
- 优点:常数小,码量小,操作灵活简便。
- 缺点:只能用来维护具有 结合律 且 可差分 的信息。例如:区间和、积等,而不能维护区间最大(最小)值。
引入
现在想要让你实现两个操作:
- 单点修改
- 查询 [ 1 , x ] [1,x] [1,x] 的和
在没有学过树状数组的时候你会怎么做?
1. 直接暴力
单点修改虽然方便,但前缀和是 O ( n ) O(n) O(n) 复杂度。
2. 维护前缀和数组
这样做虽然查询是 O ( 1 ) O(1) O(1) 了,但单点修改又是 O ( n ) O(n) O(n)。
总结
- 暴力
- 修改: O ( 1 ) O(1) O(1)
- 查询: O ( n ) O(n) O(n)
- 前缀和
- 修改: O ( n ) O(n) O(n)
- 查询: O ( 1 ) O(1) O(1)
那么我们不妨考虑一个折中的办法,两种操作都是 O ( log n ) O(\log n) O(logn) 的复杂度。
定义
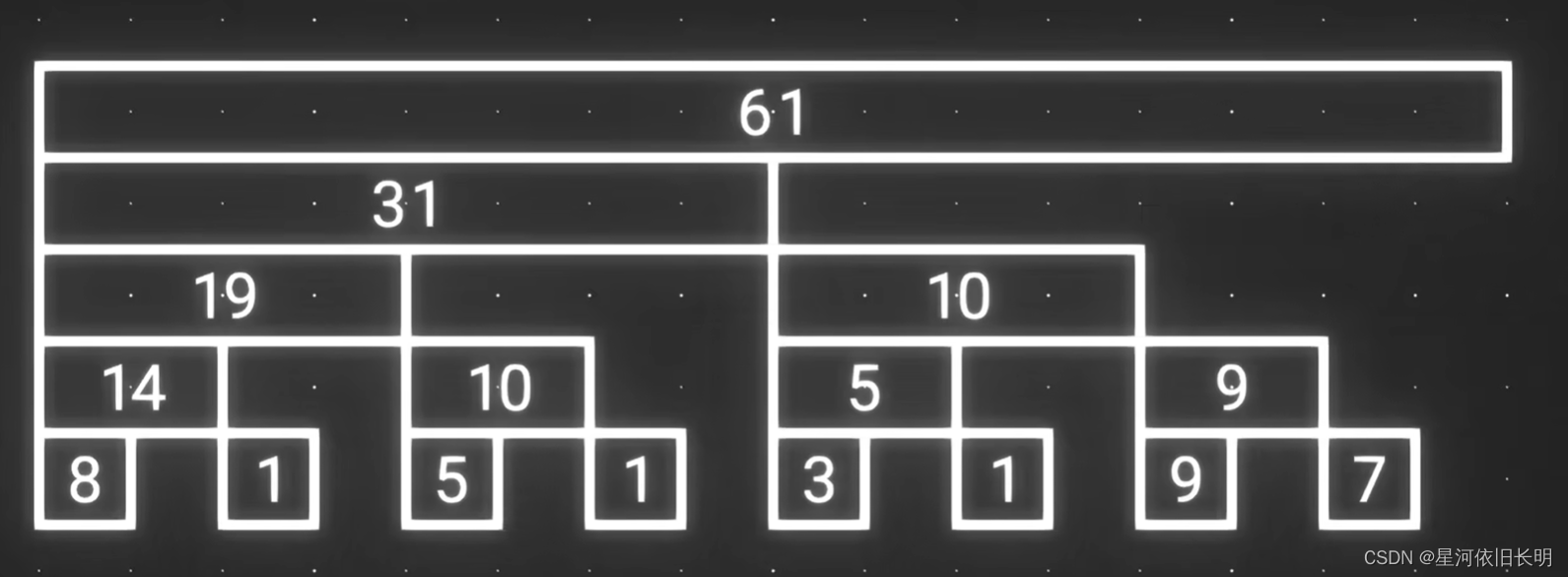
注:这里的数值表示的是该区间所有元素的和,也就是这个节点左下方的所有直接相关节点的总和。
例如:权值为 31 31 31 的节点表示的是权值分别为 19 , 10 , 1 19,10,1 19,10,1 的节点以及原数组中下表为 8 8 8 的元素之和。
显然,我们能求出原数组为
[ 8 , 6 , 1 , 4 , 5 , 5 , 1 , 1 , 3 , 2 , 1 , 4 , 9 , 0 , 7 , 4 ] [8,6,1,4,5,5,1,1,3,2,1,4,9,0,7,4] [8,6,1,4,5,5,1,1,3,2,1,4,9,0,7,4]
这里插一句话:树状数组可以近似看成线段树去掉所有右儿子构成的树。
前置知识: lowbit \operatorname{lowbit} lowbit 操作
一个二进制数的 lowbit \operatorname{lowbit} lowbit 值就是这个数末尾第一个非零的位置的权值。
举个例子: 10001 0 ( 2 ) 100010_{(2)} 100010(2)
这个数的 lowbit \operatorname{lowbit} lowbit 值是 1 0 ( 2 ) 10_{(2)} 10(2),即 2 ( 10 ) 2_{(10)} 2(10)。
那么这个怎么用代码实现呢?
void lowbit(int x)
{return x & -x;
}
什么?你问为什么这么简单??
这都不知道,赶紧退役吧 h h \color{white}{这都不知道,赶紧退役吧hh} 这都不知道,赶紧退役吧hh
这里涉及到补码的概念。
一个二进制数的补码就是其二进制上的每一位都按位取反之后再 + 1 +1 +1。
还是那个数: 10001 0 ( 2 ) 100010_{(2)} 100010(2)
先按位取反: 01110 1 ( 2 ) 011101_{(2)} 011101(2)
再加一: 1111 0 ( 2 ) 11110_{(2)} 11110(2)
我们惊奇地发现,它们的后两位竟然是一样的!!!
我们把它们进行按位与运算 &,得到的结果是 1 0 ( 2 ) 10_{(2)} 10(2),即 2 ( 10 ) 2_{(10)} 2(10),与我们刚才进行手动 lowbit \operatorname{lowbit} lowbit 运算的结果相同。
在计算机的运算过程中,由于是按照补码储存的,所以我们需要的 ~x + 1 就可以写成 -x。
因此 lowbit \operatorname{lowbit} lowbit 才能写成 x & -x。
区间的表示方法

对于每个标号为 x x x 的节点,我们发现它父节点的标号为 x + lowbit x x+\text{lowbit}\ x x+lowbit x。
而每个区间的范围都是 ( x − lowbit ( x ) , x ] (x-\text{lowbit}(x),x] (x−lowbit(x),x]。
操作
单点修改
对于每个被修改的点,我们需要找到它的所有祖先节点并都进行修改操作。
考虑到它们标号的关系,我们只要每次加一个 lowbit(x) \text{lowbit(x)} lowbit(x) 就能找到所有祖先节点了。

代码:
void add(int x, int c) // 将第 x 个数加 c
{for (int i = x; i <= n; i += lowbit(i))tr[i] += c;
}前缀和查询

实践是检验真理的唯一标准。
经过我们的实践,找到该节点前面的所有节点,只需要每次减 lowbit(x) \text{lowbit(x)} lowbit(x) 即可。
代码:
void query(int x) // 查询 1~x 的和
{int res = 0;for (int i = x; i; i -= lowbit(i))res += tr[i];return res;
}
任意区间查询
我们都知道前缀和的性质。
∑ i = l r w i = ∑ i = 1 r w i − ∑ i = 1 l − 1 w i \sum_{i=l}^{r}w_i=\sum_{i=1}^{r}w_i-\sum_{i=1}^{l-1}w_i i=l∑rwi=i=1∑rwi−i=1∑l−1wi
代码:
void Query(int l, int r) // 查询 [l,r] 的和
{return query(r) - query(l - 1);
}
例题1: 单点修改,区间查询
原题链接:P3374 【模板】树状数组 1
操作和上面的相同,直接上代码:
#include <iostream>using namespace std;const int N = 500010;int n, m;
int a[N];
int tr[N];int lowbit(int x)
{return x & -x;
}void add(int x, int c)
{for (int i = x; i <= n; i += lowbit(i))tr[i] += c;
}int sum(int x)
{int res = 0;for (int i = x; i; i -= lowbit(i))res += tr[i];return res;
}int main()
{int op, x, y;scanf("%d%d", &n, &m);for (int i = 1; i <= n; i ++ )scanf("%d", &a[i]), add(i, a[i]);while (m -- ){scanf("%d%d%d", &op, &x, &y);if (op == 1) add(x, y);else printf("%d\n", sum(y) - sum(x - 1));}return 0;
}
例题2: 区间修改,单点查询
原题链接:P3368 【模板】树状数组 2
同一道题,思路已经在昨天的 【笔记】线段树 里面讲了,无非是维护一个差分数组。
代码:
#include <iostream>using namespace std;const int N = 500010;int n, m;
int a[N], b[N];
int tr[N];int lb(int x)
{return x & -x;
}void add(int x, int v)
{for (int i = x; i <= n; i += lb(i))tr[i] += v;
}int q(int x)
{int res = 0;for (int i = x; i; i -= lb(i))res += tr[i];return res;
}int main()
{cin >> n >> m;for (int i = 1; i <= n; i ++ )cin >> a[i], b[i] = a[i] - a[i - 1], add(i, b[i]);while (m -- ){int op, x, y, k;cin >> op >> x;if (op == 1){cin >> y >> k;add(x, k), add(y + 1, -k);}else cout << q(x) << endl;}
}
例题3: 区间修改,区间查询
原题链接:P3372 【模板】线段树 1
不要说我用线段树的题练习树状数组,我找不到树状数组的模板题才用的这个
考虑用树状数组 tr[] 维护差分数组
则求原数组的前缀和
{ a 1 = d 1 a 2 = d 1 + d 2 a 3 = d 1 + d 2 + d 3 . . . . . . a n = d 1 + d 2 + . . . + d n \left\{\begin{matrix} a_1& =& d_1& & & & & & & \\ a_2& =& d_1& +& d_2& & & & & \\ a_3& =& d_1& +& d_2& +& d_3& & & \\ .& .& .& .& .& .& & & & \\ a_n& =& d_1& +& d_2& +& ...& +& d_n& \\ \end{matrix}\right. ⎩ ⎨ ⎧a1a2a3.an===.=d1d1d1.d1++.+d2d2.d2+.+d3...+dn
s i = ∑ i = 1 n a i = { d 1 d 1 + d 2 d 1 + d 2 + d 3 . . . . . . d 1 + d 2 + . . . + d n s_i=\sum_{i=1}^{n}a_i=\left\{\begin{matrix} d_1& & & & & & & \\ d_1& +& d_2& & & & & \\ d_1& +& d_2& +& d_3& & & \\ .& .& .& .& .& .& & & & \\ d_1& +& d_2& +& ...& +& d_n& \\ \end{matrix}\right. si=i=1∑nai=⎩ ⎨ ⎧d1d1d1.d1++.+d2d2.d2+.+d3.....+dn
我们考虑把后面的矩阵补全:

则
s i = ( n + 1 ) × ∑ i = 1 n d i − ∑ i = 1 n ( i × d i ) s_i=(n+1) \times \sum_{i=1}^{n}d_i-\sum_{i=1}^{n}(i \times d_i) si=(n+1)×i=1∑ndi−i=1∑n(i×di)
所以我们需要两个树状数组,tr1[] 维护差分数组,tr2[] 维护 i × d i i \times d_i i×di
代码:
#include <iostream>using namespace std;typedef long long LL;const LL N = 1000010;LL n, m;
LL a[N];
LL t1[N], t2[N];inline LL lowbit(LL x)
{return x & -x;
}inline void add(LL t[], LL x, LL c)
{for (LL i = x; i <= n; i += lowbit(i))t[i] += c;
}inline LL sum(LL t[], LL x)
{LL res = 0;for (LL i = x; i; i -= lowbit(i))res += t[i];return res;
}inline LL psum(LL x)
{return sum(t1, x) * (x + 1) - sum(t2, x);
}int main()
{scanf("%lld%lld", &n, &m);for (LL i = 1; i <= n; i ++ ) scanf("%lld", &a[i]);for (LL i = 1; i <= n; i ++ ){LL b = a[i] - a[i - 1];add(t1, i, b);add(t2, i, b * i);}while (m -- ){char op[2];LL l, r, d;scanf("%s%lld%lld", op, &l, &r);if (op[0] == '2'){printf("%lld\n", psum(r) - psum(l - 1));}else{scanf("%lld", &d);add(t1, l, d), add(t2, l, l * d);add(t1, r + 1, -d), add(t2, r + 1, -d * (r + 1));}}return 0;
}
最后,如果觉得对您有帮助的话,点个赞再走吧!
(后附极限卡常代码,70ms,较优解)
#define qwq optimize
#pragma GCC qwq(1)
#pragma GCC qwq(2)
#pragma GCC qwq(3)
#pragma GCC qwq("Ofast")
#pragma GCC qwq("inline")
#pragma GCC qwq("-fgcse")
#pragma GCC qwq("-fgcse-lm")
#pragma GCC qwq("-fipa-sra")
#pragma GCC qwq("-ftree-pre")
#pragma GCC qwq("-ftree-vrp")
#pragma GCC qwq("-fpeephole2")
#pragma GCC qwq("-ffast-math")
#pragma GCC qwq("-fsched-spec")
#pragma GCC qwq("unroll-loops")
#pragma GCC qwq("-falign-jumps")
#pragma GCC qwq("-falign-loops")
#pragma GCC qwq("-falign-labels")
#pragma GCC qwq("-fdevirtualize")
#pragma GCC qwq("-fcaller-saves")
#pragma GCC qwq("-fcrossjumping")
#pragma GCC qwq("-fthread-jumps")
#pragma GCC qwq("-funroll-loops")
#pragma GCC qwq("-fwhole-program")
#pragma GCC qwq("-freorder-blocks")
#pragma GCC qwq("-fschedule-insns")
#pragma GCC qwq("inline-functions")
#pragma GCC qwq("-ftree-tail-merge")
#pragma GCC qwq("-fschedule-insns2")
#pragma GCC qwq("-fstrict-aliasing")
#pragma GCC qwq("-fstrict-overflow")
#pragma GCC qwq("-falign-functions")
#pragma GCC qwq("-fcse-skip-blocks")
#pragma GCC qwq("-fcse-follow-jumps")
#pragma GCC qwq("-fsched-interblock")
#pragma GCC qwq("-fpartial-inlining")
#pragma GCC qwq("no-stack-protector")
#pragma GCC qwq("-freorder-functions")
#pragma GCC qwq("-findirect-inlining")
#pragma GCC qwq("-fhoist-adjacent-loads")
#pragma GCC qwq("-frerun-cse-after-loop")
#pragma GCC qwq("inline-small-functions")
#pragma GCC qwq("-finline-small-functions")
#pragma GCC qwq("-ftree-switch-conversion")
#pragma GCC qwq("-fqwq-sibling-calls")
#pragma GCC qwq("-fexpensive-optimizations")
#pragma GCC qwq("-funsafe-loop-optimizations")
#pragma GCC qwq("inline-functions-called-once")
#pragma GCC qwq("-fdelete-null-pointer-checks")
#include <iostream>
#include <cstdio>#define lb(x) (x & (-x))using namespace std;typedef long long LL;const LL N = 100010;LL n, m;
LL a[N];
LL t1[N], t2[N];char *p1, *p2, buf[N];
#define nc() (p1 == p2 && (p2 = (p1 = buf) +\
fread(buf, 1, N, stdin), p1 == p2) ? EOF : *p1 ++ )
LL read()
{LL x = 0, f = 1;char ch = nc();while (ch < 48 || ch > 57){if (ch == '-') f = -1;ch = nc();}while (ch >= 48 && ch <= 57)x = (x << 3) + (x << 1) + (ch ^ 48), ch = nc();return x * f;
}char obuf[N], *p3 = obuf;
#define putchar(x) (p3 - obuf < N) ? (*p3 ++ = x) :\
(fwrite(obuf, p3 - obuf, 1, stdout), p3 = obuf, *p3 ++ = x)
inline void write(LL x)
{if (!x){putchar('0');return;}LL len = 0, k1 = x, c[40];if (k1 < 0) k1 = -k1, putchar('-');while (k1) c[len ++ ] = k1 % 10 ^ 48, k1 /= 10;while (len -- ) putchar(c[len]);
}inline void add(LL t[], LL x, LL c)
{for (LL i = x; i <= n; i += lb(i))t[i] += c;
}inline LL sum(LL t[], LL x)
{LL res = 0;for (LL i = x; i; i -= lb(i))res += t[i];return res;
}inline LL psum(LL x)
{return sum(t1, x) * (x + 1) - sum(t2, x);
}int main()
{n = read(), m = read();for (LL i = 1; i <= n; i ++ ) a[i] = read();for (LL i = 1; i <= n; i ++ ){LL b = a[i] - a[i - 1];add(t1, i, b);add(t2, i, b * i);}LL op, l, r, d;while (m -- ){op = read(), l = read(), r = read();if (op == 2) write(psum(r) - psum(l - 1)), putchar(10);else{d = read();add(t1, l, d), add(t2, l, l * d);add(t1, r + 1, -d), add(t2, r + 1, -d * (r + 1));}}fwrite(obuf, p3 - obuf, 1, stdout);return 0;
}

相关文章:

【笔记】树状数组
【笔记】树状数组 目录 简介引入1. 直接暴力2. 维护前缀和数组总结 定义前置知识: lowbit \operatorname{lowbit} lowbit 操作区间的表示方法操作单点修改前缀和查询任意区间查询 例题1: 单点修改,区间查询例题2: 区间修改,单点查询例题3:…...
vue全局组件自动注册直接使用,无需单独先引用注册再使用
目录结构: 本案例是在根目录下components文件夹测试的,文件位置项目内任意,确保在main.js挂载路径正确即可 1、新建文件夹(名字随意)zxy_components (放自己组件的地方) 2、在zxy_components文件夹下 !新建…...

【HarmonyOS】@ohos.request 上传下载的那些事儿
【关键字】 ohos.request、上传下载 【写在前面】 在进行HarmonyOS应用开发时,可能需要进行上传或下载文件功能开发,本文章主要进行上传下载相关功能介绍和一些注意事项及FAQ。 【上传开发步骤】 步骤1:上传下载接口需要申请ohos.permis…...
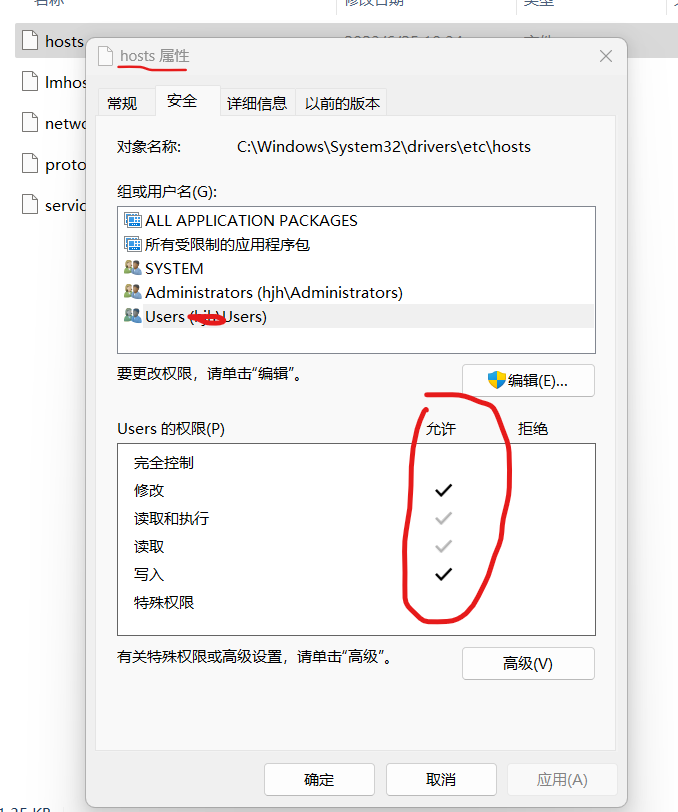
github版面混乱加载不出的解决办法
最近出现打开github 界面加载不成功,网页访问乱码,打开chrome的检查发现 github的github.githubassets.com 拒绝访问, 解法: 1.先打开hosts文件所在的目录C:\Windows\System32\drivers\etc 2.右键点击hosts文件-选择用记事本或者…...
dotNet 之数据库sqlite
Sqlite3是个特别好的本地数据库,体积小,无需安装,是写小控制台程序最佳数据库。NET Core是同样也是.NET 未来的方向。 **硬件支持型号 点击 查看 硬件支持 详情** DTU701 产品详情 DTU702 产品详情 DTU801 产品详情 DTU802 产品详情 D…...

走近ChatGPT与类似产品:原理解析与比较
目录 1. 引言1.1 技术的进步与自然语言处理1.2 ChatGPT的崭新概念 2. ChatGPT: 一览众山小2.1 GPT-3.5架构简介2.2 ChatGPT的学习与训练2.3 文本生成的工作原理 3. 市场上类似产品调研3.1 对话式人工智能产品分类3.2 文心一言3.3 讯飞星火 4. 应用前景与局限性展望4.1 ChatGPT的…...

HarmonyOS SDK开放能力,服务鸿蒙生态建设,打造优质应用体验
华为开发者大会2023(HDC.Together)于8月4日至6日在东莞松山湖举行,在HarmonyOS端云开放能力技术分论坛上,华为为广大开发者们介绍了HarmonyOS SDK开放能力在基础开发架构、功能特性等方面的变化之处,通过将常见的通用能…...

数字经济对产业结构升级和创业增长的影响(2011-2021年)
参照刘翠花(2022)的做法,对来自中国人口科学《数字经济对产业结构升级和创业增长的影响》一文中的基准回归部分进行复刻。文章从理论层面分析数字经济发展对产业结构升级、创业增长的影响及其机理,并利用2011-2021年中国省级面板数…...
GPT-4助力数据分析:提升效率与洞察力的未来关键技术 | 京东云技术团队
摘要 随着大数据时代的到来,数据分析已经成为企业和组织的核心竞争力。然而,传统的数据分析方法往往无法满足日益增长的数据分析需求的数量和复杂性。在这种背景下,ChatGPT-4作为一种先进的自然语言处理技术,为数据分析带来了革命…...
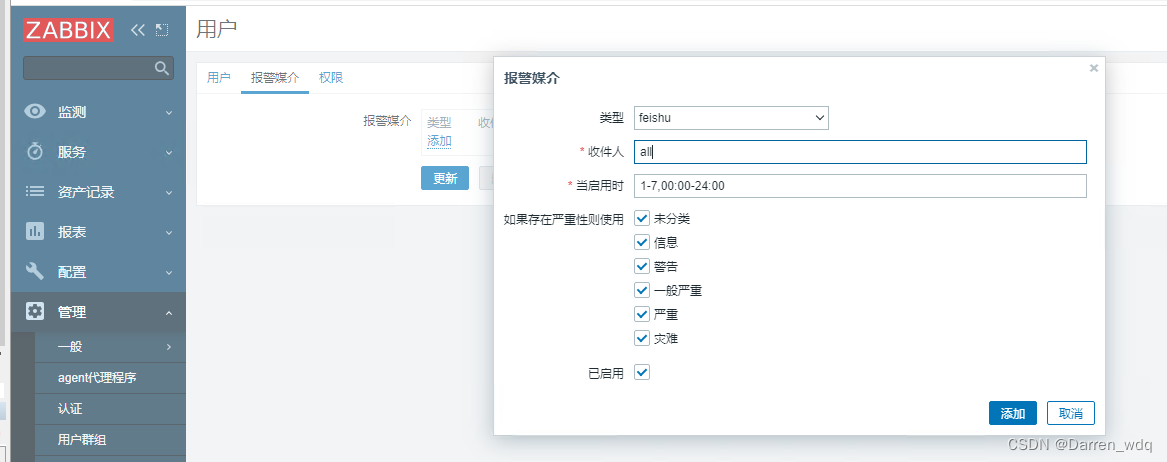
Zabbix6 对接飞书告警
文章目录 Zabbix对接飞书告警背景创建飞书群组Zabbix配置创建告警媒介类型创建动作用户关联飞书告警 Zabbix对接飞书告警 背景 运维 你看下他的进程是不是挂了,之前在9点28分有发消息的,这次没有发消息 哐哐哐的去看了一通,确实有个进程之前…...

Javascript异步编程的4种方法
你可能知道,Javascript语言的执行环境是"单线程"(single thread)。 所谓"单线程",就是指一次只能完成一件任务。如果有多个任务,就必须排队,前面一个任务完成,再执行后面一…...

【MySQL】表的内外连接
目录 一、内连接 二、外连接 1、左外连接 2、右外连接 一、内连接 内连接实际上就是利用where子句对两种表形成的笛卡儿积进行筛选,我们前面学习的查询都是内连接,也是在开发过程中使用的最多的连接查询。 语法: select 字段 from 表1 i…...
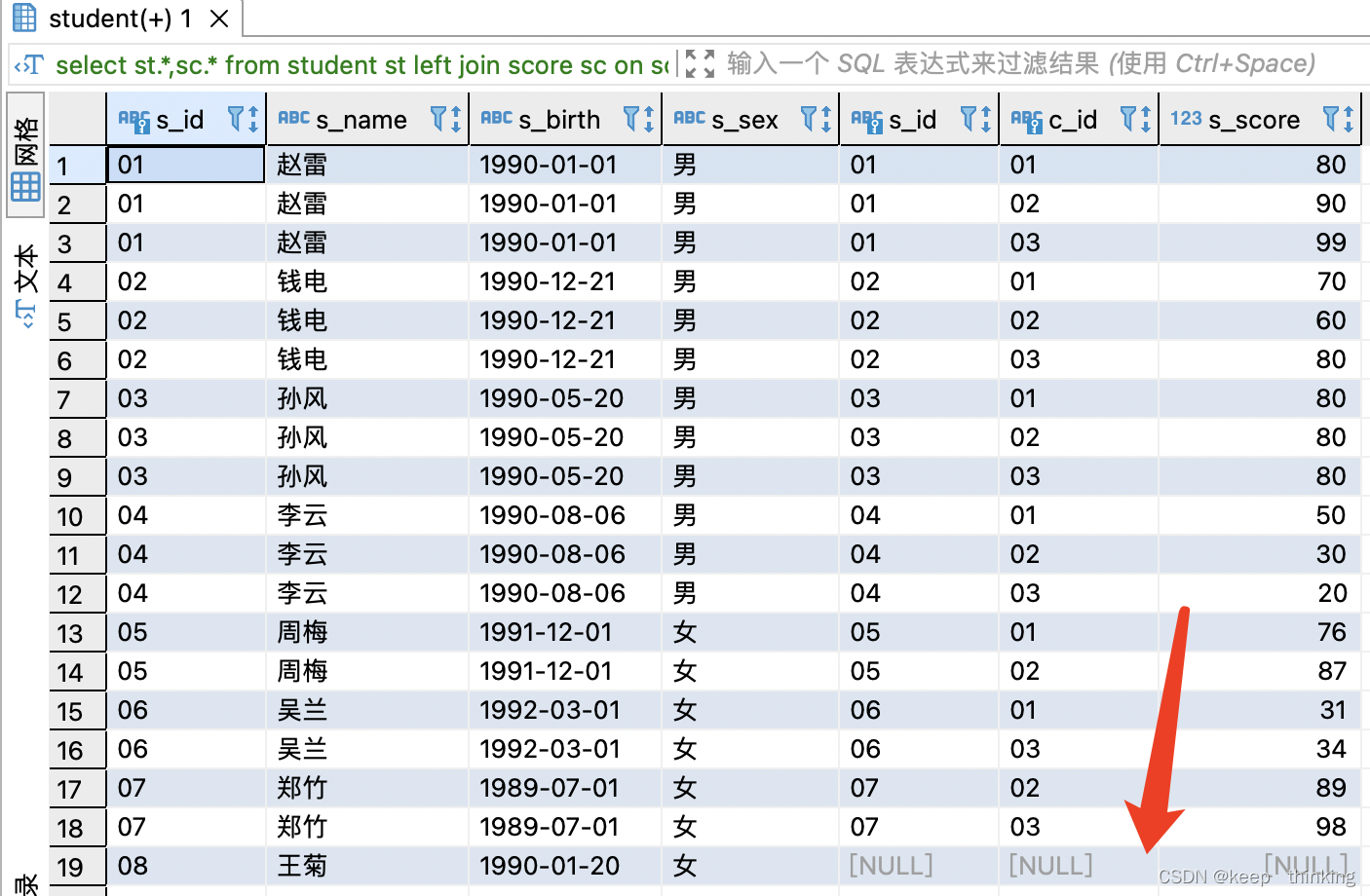
详解Mysql——第一篇/连接查询
mysql的连接查询,相必在网上都能找到很多的教程,博主今天不做老话常谈,不走重复路线 1.建表 –1.学生表 Student(s_id,s_name,s_birth,s_sex) –学生编号,学生姓名, 出生年月,学生性别 –2.课程表 Course(c_id,c_name,t_id) – –课程编…...

uniapp获取屏幕宽度时 获取不到移动设备中内容盒子宽度
首先 :我使用的是uniapp vue3语法: 问题: 我出现这个问题是IOS 设备发现的,data.boxWidth为0 代码: const initCreated () > {const query uni.createSelectorQuery().in(instance.proxy);const el query.select…...

篇十二:代理模式:控制对象访问
篇十二:“代理模式:控制对象访问” 开始本篇文章之前先推荐一个好用的学习工具,AIRIght,借助于AI助手工具,学习事半功倍。欢迎访问:http://airight.fun/。 另外有2本不错的关于设计模式的资料,…...

P1657 选书
1:思路:一看数据,嗯....!,爆搜嘛?,看一眼题目,嗯!!!,爆搜! 配上俺的无敌小剪枝,按下拿下! 2:暴力枚举每个人获…...

代码随想录第46天 | 139. 单词拆分、多重背包
139. 单词拆分 确定dp数组以及下标的含义 dp[i] : 字符串长度为i的话,dp[i]为true,表示可以拆分为一个或多个在字典中出现的单词。 确定递推公式 如果确定dp[j] 是true,且 [j, i] 这个区间的子串出现在字典里,那么dp[i]一定是tru…...
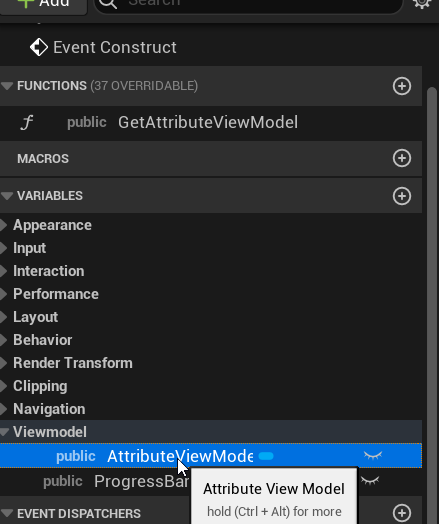
Unreal View Model结合GAS使用
这个东西真的难用,各种问题,记录下 官方文档 bilibili教学 开启插件 插件开启 Viewmodel: build.cs内PublicDependencyModuleNames加上ModelViewViewModel 创建ViewModel类 #pragma once#include "CoreMinimal.h" #include &quo…...
Spring-Cloud-Loadblancer详细分析_2
LoadBalancerClients 终于分析到了此注解的作用,它是实现不同服务之间的配置隔离的关键 Configuration(proxyBeanMethods false) Retention(RetentionPolicy.RUNTIME) Target({ ElementType.TYPE }) Documented Import(LoadBalancerClientConfigurationRegistrar…...
uniapp 左右滑动切换页面并切换tab
实现效果如图 要实现底部内部的左右滑动切换带动上方tab栏的切换,并且下方内容要实现纵向滚动 ,所以需要swiper,swiper-item,scroll-view组合使用 tab栏部分 <view class"tabs"><view class"tab_item" v-for&…...

SpringBoot-17-MyBatis动态SQL标签之常用标签
文章目录 1 代码1.1 实体User.java1.2 接口UserMapper.java1.3 映射UserMapper.xml1.3.1 标签if1.3.2 标签if和where1.3.3 标签choose和when和otherwise1.4 UserController.java2 常用动态SQL标签2.1 标签set2.1.1 UserMapper.java2.1.2 UserMapper.xml2.1.3 UserController.ja…...

AI-调查研究-01-正念冥想有用吗?对健康的影响及科学指南
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

练习(含atoi的模拟实现,自定义类型等练习)
一、结构体大小的计算及位段 (结构体大小计算及位段 详解请看:自定义类型:结构体进阶-CSDN博客) 1.在32位系统环境,编译选项为4字节对齐,那么sizeof(A)和sizeof(B)是多少? #pragma pack(4)st…...

【入坑系列】TiDB 强制索引在不同库下不生效问题
文章目录 背景SQL 优化情况线上SQL运行情况分析怀疑1:执行计划绑定问题?尝试:SHOW WARNINGS 查看警告探索 TiDB 的 USE_INDEX 写法Hint 不生效问题排查解决参考背景 项目中使用 TiDB 数据库,并对 SQL 进行优化了,添加了强制索引。 UAT 环境已经生效,但 PROD 环境强制索…...

java 实现excel文件转pdf | 无水印 | 无限制
文章目录 目录 文章目录 前言 1.项目远程仓库配置 2.pom文件引入相关依赖 3.代码破解 二、Excel转PDF 1.代码实现 2.Aspose.License.xml 授权文件 总结 前言 java处理excel转pdf一直没找到什么好用的免费jar包工具,自己手写的难度,恐怕高级程序员花费一年的事件,也…...

全球首个30米分辨率湿地数据集(2000—2022)
数据简介 今天我们分享的数据是全球30米分辨率湿地数据集,包含8种湿地亚类,该数据以0.5X0.5的瓦片存储,我们整理了所有属于中国的瓦片名称与其对应省份,方便大家研究使用。 该数据集作为全球首个30米分辨率、覆盖2000–2022年时间…...

页面渲染流程与性能优化
页面渲染流程与性能优化详解(完整版) 一、现代浏览器渲染流程(详细说明) 1. 构建DOM树 浏览器接收到HTML文档后,会逐步解析并构建DOM(Document Object Model)树。具体过程如下: (…...

2025 后端自学UNIAPP【项目实战:旅游项目】6、我的收藏页面
代码框架视图 1、先添加一个获取收藏景点的列表请求 【在文件my_api.js文件中添加】 // 引入公共的请求封装 import http from ./my_http.js// 登录接口(适配服务端返回 Token) export const login async (code, avatar) > {const res await http…...

《基于Apache Flink的流处理》笔记
思维导图 1-3 章 4-7章 8-11 章 参考资料 源码: https://github.com/streaming-with-flink 博客 https://flink.apache.org/bloghttps://www.ververica.com/blog 聚会及会议 https://flink-forward.orghttps://www.meetup.com/topics/apache-flink https://n…...

工业自动化时代的精准装配革新:迁移科技3D视觉系统如何重塑机器人定位装配
AI3D视觉的工业赋能者 迁移科技成立于2017年,作为行业领先的3D工业相机及视觉系统供应商,累计完成数亿元融资。其核心技术覆盖硬件设计、算法优化及软件集成,通过稳定、易用、高回报的AI3D视觉系统,为汽车、新能源、金属制造等行…...
