并查集、树状数组
并查集、树状数组、线段树
- 并查集
- 树状数组
- 树状数组1 (单点修改,区间查询)
- 树状数组2 (单点查询,区间修改)
并查集
【模板】并查集
题目描述
如题,现在有一个并查集,你需要完成合并和查询操作。
输入格式
第一行包含两个整数 N , M N,M N,M ,表示共有 N N N 个元素和 M M M 个操作。
接下来 M M M 行,每行包含三个整数 Z i , X i , Y i Z_i,X_i,Y_i Zi,Xi,Yi 。
当 Z i = 1 Z_i=1 Zi=1 时,将 X i X_i Xi 与 Y i Y_i Yi 所在的集合合并。
当 Z i = 2 Z_i=2 Zi=2 时,输出 X i X_i Xi 与 Y i Y_i Yi 是否在同一集合内,是的输出
Y ;否则输出 N 。
输出格式
对于每一个 Z i = 2 Z_i=2 Zi=2 的操作,都有一行输出,每行包含一个大写字母,为 Y 或者 N 。
样例输入 #1
4 7
2 1 2
1 1 2
2 1 2
1 3 4
2 1 4
1 2 3
2 1 4
样例输出 #1
N
Y
N
Y
提示
对于 30 % 30\% 30% 的数据, N ≤ 10 N \le 10 N≤10, M ≤ 20 M \le 20 M≤20。
对于 70 % 70\% 70% 的数据, N ≤ 100 N \le 100 N≤100, M ≤ 1 0 3 M \le 10^3 M≤103。
对于 100 % 100\% 100% 的数据, 1 ≤ N ≤ 1 0 4 1\le N \le 10^4 1≤N≤104, 1 ≤ M ≤ 2 × 1 0 5 1\le M \le 2\times 10^5 1≤M≤2×105, 1 ≤ X i , Y i ≤ N 1 \le X_i, Y_i \le N 1≤Xi,Yi≤N, Z i ∈ { 1 , 2 } Z_i \in \{ 1, 2 \} Zi∈{1,2}。
以下是模板代码
#include<bits/stdc++.h>
using namespace std;
#define MAXN 10005int fa[MAXN]; // 用于存储每个元素所属的集合的根节点// 查找操作,返回元素x所属集合的根节点
int find(int x) {if(x == fa[x]) return x; // 如果当前节点是根节点,直接返回return fa[x] = find(fa[x]); // 路径压缩,将x的父节点直接设为根节点,加快以后的查找
}// 合并操作,将两个集合合并
void join(int c1, int c2) {int f1 = find(c1); // 查找c1所属的集合的根节点int f2 = find(c2); // 查找c2所属的集合的根节点if(f1 != f2) // 如果根节点不同,表示c1和c2不在同一集合中fa[f1] = f2; // 将c1的根节点的父节点设为c2的根节点,即合并两个集合
}int main() {int n, m;cin >> n >> m; // 输入元素个数n和操作个数mfor(int i = 1; i <= n; i++) fa[i] = i; // 初始化,每个元素初始时都是一个单独的集合,根节点就是自己while(m--) {int z, x, y;cin >> z >> x >> y; // 输入操作类型z以及两个元素x和yif(z == 1) {join(x, y); // 合并操作,将x和y所在的集合合并} else {if(find(x) == find(y))cout << "Y" << endl; // 查找操作,如果x和y在同一个集合中,输出Yelsecout << "N" << endl; // 否则输出N}}return 0;
}
树状数组
树状数组1 (单点修改,区间查询)
【模板】树状数组 1
题目描述
如题,已知一个数列,你需要进行下面两种操作:
-
将某一个数加上 x x x
-
求出某区间每一个数的和
输入格式
第一行包含两个正整数 n , m n,m n,m,分别表示该数列数字的个数和操作的总个数。
第二行包含 n n n 个用空格分隔的整数,其中第 i i i 个数字表示数列第 i i i 项的初始值。
接下来 m m m 行每行包含 3 3 3 个整数,表示一个操作,具体如下:
-
1 x k含义:将第 x x x 个数加上 k k k -
2 x y含义:输出区间 [ x , y ] [x,y] [x,y] 内每个数的和
输出格式
输出包含若干行整数,即为所有操作 2 2 2 的结果。
样例输入 #1
5 5
1 5 4 2 3
1 1 3
2 2 5
1 3 -1
1 4 2
2 1 4
样例输出 #1
14
16
提示
【数据范围】
对于 30 % 30\% 30% 的数据, 1 ≤ n ≤ 8 1 \le n \le 8 1≤n≤8, 1 ≤ m ≤ 10 1\le m \le 10 1≤m≤10;
对于 70 % 70\% 70% 的数据, 1 ≤ n , m ≤ 1 0 4 1\le n,m \le 10^4 1≤n,m≤104;
对于 100 % 100\% 100% 的数据, 1 ≤ n , m ≤ 5 × 1 0 5 1\le n,m \le 5\times 10^5 1≤n,m≤5×105。
数据保证对于任意时刻, a a a 的任意子区间(包括长度为 1 1 1 和 n n n 的子区间)和均在 [ − 2 31 , 2 31 ) [-2^{31}, 2^{31}) [−231,231) 范围内。
样例说明:
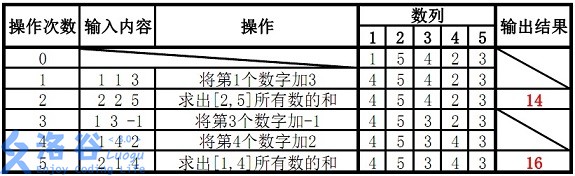
故输出结果14、16
以下是模板代码
#include<bits/stdc++.h>
using namespace std;
const int N = 5e5 + 5;
#define lowbit(x) ((x) & (-x))
int tree[N] = {0}; // 树状数组void update(int x, int d) { // 单点修改:修改元素 a[x],a[x] = a[x] + dwhile (x <= N) {tree[x] += d; // 将当前位置的值增加dx += lowbit(x); // 转到下一个需要修改的位置}
}int sum(int x) { // 查询前缀和:返回前缀和 sum = a[1] + a[2] + ... + a[x]int ans = 0;while (x > 0) {ans += tree[x]; // 累加当前位置的值x -= lowbit(x); // 转到前一个位置}return ans;
}int main() {int n, m, a;cin >> n >> m; // 输入数列数字个数n和操作总个数mfor (int i = 1; i <= n; i++) {cin >> a; // 输入每个数列项的初始值update(i, a); // 初始化计算tree[]数组}while (m--) {int op;cin >> op; // 输入操作类型if (op == 1) {int x, k;cin >> x >> k; // 输入要修改的元素位置x和要加的值kupdate(x, k); // 对位置x的元素进行加法操作} else {int x, y;cin >> x >> y; // 输入查询区间[x, y]cout << sum(y) - sum(x - 1) << endl; // 输出区间内元素和}}return 0;
}树状数组2 (单点查询,区间修改)
【模板】树状数组 2
题目描述
如题,已知一个数列,你需要进行下面两种操作:
-
将某区间每一个数加上 x x x;
-
求出某一个数的值。
输入格式
第一行包含两个整数 N N N、 M M M,分别表示该数列数字的个数和操作的总个数。
第二行包含 N N N 个用空格分隔的整数,其中第 i i i 个数字表示数列第 $i $ 项的初始值。
接下来 M M M 行每行包含 2 2 2 或 4 4 4个整数,表示一个操作,具体如下:
操作 1 1 1: 格式:1 x y k 含义:将区间 [ x , y ] [x,y] [x,y] 内每个数加上 k k k;
操作 2 2 2: 格式:2 x 含义:输出第 x x x 个数的值。
输出格式
输出包含若干行整数,即为所有操作 2 2 2 的结果。
样例输入 #1
5 5
1 5 4 2 3
1 2 4 2
2 3
1 1 5 -1
1 3 5 7
2 4
样例输出 #1
6
10
提示
样例 1 解释:

故输出结果为 6、10。
数据规模与约定
对于 30 % 30\% 30% 的数据: N ≤ 8 N\le8 N≤8, M ≤ 10 M\le10 M≤10;
对于 70 % 70\% 70% 的数据: N ≤ 10000 N\le 10000 N≤10000, M ≤ 10000 M\le10000 M≤10000;
对于 100 % 100\% 100% 的数据: 1 ≤ N , M ≤ 500000 1 \leq N, M\le 500000 1≤N,M≤500000, 1 ≤ x , y ≤ n 1 \leq x, y \leq n 1≤x,y≤n,保证任意时刻序列中任意元素的绝对值都不大于 2 30 2^{30} 230。
以下是模板代码
#include<bits/stdc++.h>
using namespace std;
const int N = 5e5 + 5;
#define lowbit(x) ((x) & (-x))
int tree[N] = {0}; // 树状数组void update(int x, int d) { // 单点修改:修改元素 a[x],a[x] = a[x] + dwhile (x <= N) {tree[x] += d; // 将当前位置的值增加dx += lowbit(x); // 转到下一个需要修改的位置}
}int sum(int x) { // 查询前缀和:返回前缀和 sum = a[1] + a[2] + ... + a[x]int ans = 0;while (x > 0) {ans += tree[x]; // 累加当前位置的值x -= lowbit(x); // 转到前一个位置}return ans;
}int main() {int n, m;int old = 0, a;cin >> n >> m; // 输入数列数字个数n和操作总个数mfor (int i = 1; i <= n; i++) {cin >> a; // 输入每个数列项的初始值update(i, a - old); // 初始化计算tree[]数组,这里是一个差分数组old = a;}while (m--) {int op;cin >> op; // 输入操作类型if (op == 1) {int x, y, k;cin >> x >> y >> k; // 输入要修改的区间[x, y]和要加的值kupdate(x, k);update(y + 1, -k); // 将区间[y+1, n]的值减去k,保持区间[x, y]加上k} else {int x;cin >> x; // 输入要查询的位置xcout << sum(x) << endl; // 输出第x个数的值}}return 0;
}相关文章:

并查集、树状数组
并查集、树状数组、线段树 并查集树状数组树状数组1 (单点修改,区间查询)树状数组2 (单点查询,区间修改) 并查集 【模板】并查集 题目描述 如题,现在有一个并查集,你需要完成合并和查询操作。 输入格式 第一行包含两个整数 …...
正确打开方式-)
ES6中Null判断运算符(??)正确打开方式-
读取对象属性的时候,如果某个属性的值是null或者undefined,有时候需要为它们指定默认值。常见的作法是通过||运算符指定默认值。 const headerText response.settings.headerText || Hello, world!; const animationDuration response.settings.anima…...
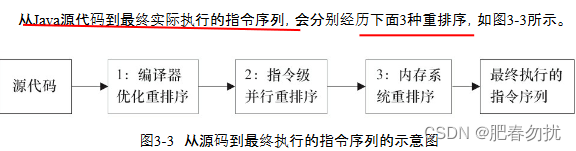
java的内存模型
Java内存基础 并发编程模型的两个关键问题 线程之间如何通信及线程之间如何同步 线程之间的通信机制有两种:共享内存和消息传递。 在共享内存的并发模型里,线程之间共享程序的公共状态,通过写-读内存中的公共状态 进行隐式通信。在消息传…...
基于 CentOS 7 构建 LVS-DR 群集 配置nginx负载均衡
环境配置: RHCE客户机192.168.100.146node1lvs192.168.100.145node2RS192.168.100.147node3RS192.168.100.148 配置ipvsadm httpd: [rootnode1 ~]# yum install ipvsadm.x86_64 [rootnode2 ~]# yum install http -y [rootnode2 ~]# systemctl …...

CSS练习
CSS练习 工具代码运行结果 工具 HBuilder X 代码 <!DOCTYPE html> <!-- 做一个表格,6行4列实现隔行换色(背景色)并且第3列文字红色第一个单元格文字大小30px。最后一个单元格文字加粗--> <html><head><meta ch…...

基于深度学习的3D城市模型增强【Mask R-CNN】
在这篇文章中,我们描述了一个为阿姆斯特丹 3D 城市模型自动添加门窗的系统(可以在这里访问)。 计算机视觉用于从城市全景图像中提取有关门窗位置的信息。 由于这种类型的街道级图像广泛可用,因此该方法可用于较大的地理区域。 推荐…...
LabVIEW对并行机器人结构进行建模仿真
LabVIEW对并行机器人结构进行建模仿真 为了对复杂机器人结构的数学模型进行建模、搜索、动画和验证,在工业机器人动态行为实验室中,设计并实现了具有五个自由度的单臂型机器人。在研究台上可以区分以下元素:带有直流电机和编码器的机器人;稳…...

【算法题】1281. 整数的各位积和之差
题目: 给你一个整数 n,请你帮忙计算并返回该整数「各位数字之积」与「各位数字之和」的差。 示例 1: 输入:n 234 输出:15 解释: 各位数之积 2 * 3 * 4 24 各位数之和 2 3 4 9 结果 24 - 9 15 示…...
ES6 介绍)
(一)ES6 介绍
为什么学习ES6 ES6的版本变动内容最多,具有里程碑意义ES加入许多新的语法特性,编程实现更简单、搞笑ES6是前端发展趋势,就业必备技能 什么是ECMA ECMA(European Computer Manufacturers Association),中…...
)
窥孔优化(Peephole Optimization)
窥孔优化(Peephole Optimization)是编译器中的一个技术,用于优化生成的中间代码或目标代码。该优化方法通过查看代码的小部分(或称为“窥孔”)来识别并提供更高效的代码替代方案。 1. 基本概念 定义:窥孔优…...

Docker安装ElasticSearch/ES 7.4.0
目录 前言安装ElasticSearch/ES安装步骤1:准备1. 安装docker2. 搜索可以使用的镜像。3. 也可从docker hub上搜索镜像。4. 选择合适的redis镜像。 安装步骤2:拉取ElasticSearch镜像1 拉取镜像2 查看已拉取的镜像 安装步骤3:创建容器创建容器方…...

无涯教程-Perl - readline函数
描述 此函数从EXPR引用的文件句柄中读取一行,并返回输出。如果要直接使用FILEHANDLE,则必须将其作为typeglob传递。 Simply readline function is equvivalent to <>. 语法 以下是此函数的简单语法- readline EXPR返回值 此函数在标量context中仅返回一行,而在列表…...
)
类与对象(入门)
目录 1.前言 2.类的引入 3.类的定义 4.类的访问限定符及封装 4.1 访问限定符 4.2 封装 5.类的作用域 6.类的实例化 7. 结构体内存对齐规则 8.this指针 8.1 this指针的引出 8.2 this指针的特性 1.前言 C 是 基于面向对象 的, 关注 的是 对象 ,…...
刷题记录(2023-08-12)
1. 小美的排列询问 AC代码: #include <iostream> #include <vector> using namespace std;int main() {int n;cin >> n;vector<int> nums(n);int a, b;for (int i 0; i < n; i) {cin >> nums[i];}cin >> a >> b;for…...

GPT内功心法:搜索思维到GPT思维的转换
大家好,我是herosunly。985院校硕士毕业,现担任算法研究员一职,热衷于机器学习算法研究与应用。曾获得阿里云天池比赛第一名,CCF比赛第二名,科大讯飞比赛第三名。拥有多项发明专利。对机器学习和深度学习拥有自己独到的见解。曾经辅导过若干个非计算机专业的学生进入到算法…...
在WebStorm中通过live-server插件搭建Ajax运行环境
1.下载node.js 官网: https://nodejs.cn/download/ 2.配置Node.js的HTTPS 使用淘宝的镜像: npm config set registry https://registry.npm.taobao.org 也可以使用cnpm npm install -g cnpm --registryhttps://registry.npm.taobao.org 配置之后可以验证是否成…...

侯捷 C++ part2 兼谈对象模型笔记——1 转换
1 转换 1.1 转换函数 将当前对象的类型转换成其他类型 以 operator 开头,函数名称为需要转成的类型,无参数前面不需要写返回类型,编译器会自动根据函数名称进行补充转换函数中,分子分母都没改变,所以通常加 const …...
尚硅谷大数据项目《在线教育之采集系统》笔记003
视频地址:尚硅谷大数据项目《在线教育之采集系统》_哔哩哔哩_bilibili 目录 P036 P037 P038 P039 P041 P042 P043 P044 P045 P046 P036 先启动zookeeper,在启动kafka,启动hadoop中的hdfs node003启动flume,node001启动f…...
刷题指南 —— 第七弹)
PAT(Advanced Level)刷题指南 —— 第七弹
一、1012 The Best Rank 1. 问题重述 排序问题,原题叙述比较清晰,按照A > C > M > E四种排序的最高名次以及对应的排序方式输出。 2. Sample Input 5 6 310101 98 85 88 310102 70 95 88 310103 82 87 94<...

合宙Air724UG LuatOS-Air script lib API--sys
sys Table of Contents sys sys.restart sys.wait(ms) sys.waitUntil(id, ms) sys.waitUntilExt(id, ms) sys.taskInit(fun, …) sys.init(mode, lprfnc) sys.timerStop(val, …) sys.timerStopAll(fnc) sys.timerStart(fnc, ms, …) sys.timerLoopStart(fnc, ms, …) sys.time…...

HTML 语义化
目录 HTML 语义化HTML5 新特性HTML 语义化的好处语义化标签的使用场景最佳实践 HTML 语义化 HTML5 新特性 标准答案: 语义化标签: <header>:页头<nav>:导航<main>:主要内容<article>&#x…...

iOS 26 携众系统重磅更新,但“苹果智能”仍与国行无缘
美国西海岸的夏天,再次被苹果点燃。一年一度的全球开发者大会 WWDC25 如期而至,这不仅是开发者的盛宴,更是全球数亿苹果用户翘首以盼的科技春晚。今年,苹果依旧为我们带来了全家桶式的系统更新,包括 iOS 26、iPadOS 26…...

微信小程序之bind和catch
这两个呢,都是绑定事件用的,具体使用有些小区别。 官方文档: 事件冒泡处理不同 bind:绑定的事件会向上冒泡,即触发当前组件的事件后,还会继续触发父组件的相同事件。例如,有一个子视图绑定了b…...

【OSG学习笔记】Day 18: 碰撞检测与物理交互
物理引擎(Physics Engine) 物理引擎 是一种通过计算机模拟物理规律(如力学、碰撞、重力、流体动力学等)的软件工具或库。 它的核心目标是在虚拟环境中逼真地模拟物体的运动和交互,广泛应用于 游戏开发、动画制作、虚…...

从零实现富文本编辑器#5-编辑器选区模型的状态结构表达
先前我们总结了浏览器选区模型的交互策略,并且实现了基本的选区操作,还调研了自绘选区的实现。那么相对的,我们还需要设计编辑器的选区表达,也可以称为模型选区。编辑器中应用变更时的操作范围,就是以模型选区为基准来…...

在rocky linux 9.5上在线安装 docker
前面是指南,后面是日志 sudo dnf config-manager --add-repo https://download.docker.com/linux/centos/docker-ce.repo sudo dnf install docker-ce docker-ce-cli containerd.io -y docker version sudo systemctl start docker sudo systemctl status docker …...

UDP(Echoserver)
网络命令 Ping 命令 检测网络是否连通 使用方法: ping -c 次数 网址ping -c 3 www.baidu.comnetstat 命令 netstat 是一个用来查看网络状态的重要工具. 语法:netstat [选项] 功能:查看网络状态 常用选项: n 拒绝显示别名&#…...

[ICLR 2022]How Much Can CLIP Benefit Vision-and-Language Tasks?
论文网址:pdf 英文是纯手打的!论文原文的summarizing and paraphrasing。可能会出现难以避免的拼写错误和语法错误,若有发现欢迎评论指正!文章偏向于笔记,谨慎食用 目录 1. 心得 2. 论文逐段精读 2.1. Abstract 2…...

MVC 数据库
MVC 数据库 引言 在软件开发领域,Model-View-Controller(MVC)是一种流行的软件架构模式,它将应用程序分为三个核心组件:模型(Model)、视图(View)和控制器(Controller)。这种模式有助于提高代码的可维护性和可扩展性。本文将深入探讨MVC架构与数据库之间的关系,以…...

大模型多显卡多服务器并行计算方法与实践指南
一、分布式训练概述 大规模语言模型的训练通常需要分布式计算技术,以解决单机资源不足的问题。分布式训练主要分为两种模式: 数据并行:将数据分片到不同设备,每个设备拥有完整的模型副本 模型并行:将模型分割到不同设备,每个设备处理部分模型计算 现代大模型训练通常结合…...
