从一个GPU到多个GPU
在多GPU运行应用程序时,需要正确设计GPU之间的通信,GPU间数据传输的效率取决于GPU是如何连接在一个节点上并跨集群的
在多GPU系统里有两种连接方式
多GPU通过单个节点连接到PCIe总线上
多GPU连接到集群中的网络交换机上
/*
* 本示例演示了如何使用 OpenMP API 为多个 GPU 编写应用程序在 CPU 端使用 OpenMP 进行线程处理的多 GPU 示例, 需要支持 OpenMP 2.0 的编译器*/#include <omp.h>
#include <stdio.h> // 使用 stdio 函数,因为 C++ 流不一定是线程安全的
#include <helper_cuda.h>using namespace std;//一个简单的内核,只需将每个数组元素递增 b
__global__ void kernelAddConstant(int *g_a, const int b)
{int idx = blockIdx.x * blockDim.x + threadIdx.x;g_a[idx] += b;
}
// 一个谓词,用于检查每个数组元素是否被设置为其索引加上 b
int correctResult(int *data, const int n, const int b)
{for (int i = 0; i < n; i++)if (data[i] != i + b)return 0;return 1;
}
int main(int argc, char *argv[])
{int num_gpus = 0; // CUDA GPU 数量printf("%s Starting...\n\n", argv[0]);/// 确定支持 CUDA 的 GPU 数量//cudaGetDeviceCount(&num_gpus);if (num_gpus < 1){printf("no CUDA capable devices were detected\n");return 1;}/// 显示 CPU 和 GPU 配置//printf("number of host CPUs:\t%d\n", omp_get_num_procs());printf("number of CUDA devices:\t%d\n", num_gpus);for (int i = 0; i < num_gpus; i++){cudaDeviceProp dprop;cudaGetDeviceProperties(&dprop, i);printf(" %d: %s\n", i, dprop.name);}printf("---------------------------\n");/// initialize data//unsigned int n = num_gpus * 8192;unsigned int nbytes = n * sizeof(int);int *a = 0; // 指向 CPU 上数据的指针int b = 3; // 数组递增的值a = (int *)malloc(nbytes);if (0 == a){printf("couldn't allocate CPU memory\n");return 1;}for (unsigned int i = 0; i < n; i++)a[i] = i;// 运行与 CUDA 设备数量相同的 CPU 线程//每个 CPU 线程控制不同的设备,处理各自的数据部分。 // 使用的 CPU 线程数量有可能多于 CUDA 设备的数量,在这种情况下,多个 CPU 线程将在同一设备上分配资源并启动内核。// 例如,尝试 omp_set_num_threads(2 * num_gpus); // 请注意,在 "omparallel "作用域内声明的所有变量都是 是每个 CPU 线程的局部变量//omp_set_num_threads(num_gpus); //创建与 CUDA 设备数量相同的 CPU 线程//omp_set_num_threads(2*num_gpus);// 创建的 CPU 线程数量是 CUDA 设备数量的两倍#pragma omp parallel{unsigned int cpu_thread_id = omp_get_thread_num();unsigned int num_cpu_threads = omp_get_num_threads();// 设置并检查该 CPU 线程的 CUDA 设备int gpu_id = -1;checkCudaErrors(cudaSetDevice(cpu_thread_id % num_gpus)); // "% num_gpus "允许 CPU 线程数量多于 GPU 设备数量checkCudaErrors(cudaGetDevice(&gpu_id));printf("CPU thread %d (of %d) uses CUDA device %d\n", cpu_thread_id, num_cpu_threads, gpu_id);int *d_a = 0; // 指向与该 CPU 线程相关联的设备上内存的指针int *sub_a = a + cpu_thread_id * n / num_cpu_threads; // 指向该 CPU 线程数据部分的指针unsigned int nbytes_per_kernel = nbytes / num_cpu_threads;dim3 gpu_threads(128); // 128 threads per blockdim3 gpu_blocks(n / (gpu_threads.x * num_cpu_threads));checkCudaErrors(cudaMalloc((void **)&d_a, nbytes_per_kernel));checkCudaErrors(cudaMemset(d_a, 0, nbytes_per_kernel));checkCudaErrors(cudaMemcpy(d_a, sub_a, nbytes_per_kernel, cudaMemcpyHostToDevice));kernelAddConstant<<<gpu_blocks, gpu_threads>>>(d_a, b);checkCudaErrors(cudaMemcpy(sub_a, d_a, nbytes_per_kernel, cudaMemcpyDeviceToHost));checkCudaErrors(cudaFree(d_a));}printf("---------------------------\n");if (cudaSuccess != cudaGetLastError())printf("%s\n", cudaGetErrorString(cudaGetLastError()));// check the result//bool bResult = correctResult(a, n, b);if (a)free(a); // free CPU memoryexit(bResult ? EXIT_SUCCESS : EXIT_FAILURE);
}
相关文章:

从一个GPU到多个GPU
在多GPU运行应用程序时,需要正确设计GPU之间的通信,GPU间数据传输的效率取决于GPU是如何连接在一个节点上并跨集群的 在多GPU系统里有两种连接方式 多GPU通过单个节点连接到PCIe总线上 多GPU连接到集群中的网络交换机上 /* * 本示例演示了如何使用 Open…...

小白编写一个Chrome
步骤 1:了解插件的基本结构和功能 首先,向小白解释什么是Chrome插件,它是如何工作的,以及它可以做什么。强调插件可以修改网页内容、添加功能等。 步骤 2:准备工作 安装Chrome浏览器:确保小白的计算机上…...
自然语言处理学习笔记(六)————字典树
目录 1.字典树 (1)为什么引入字典树 (2)字典树定义 (3)字典树的节点实现 (4)字典树的增删改查 DFA(确定有穷自动机) (5)优化 1.…...
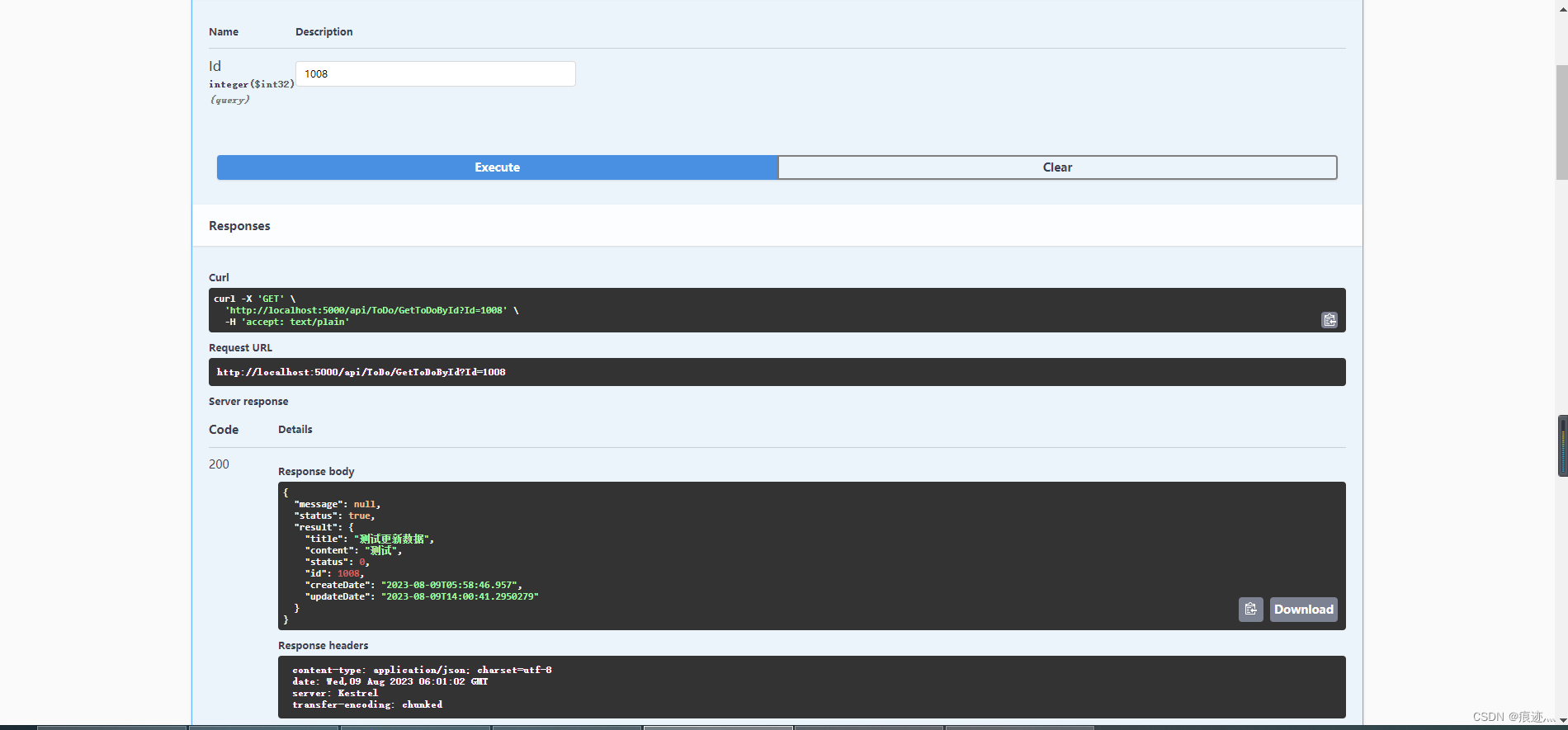
WPF实战项目十一(API篇):待办事项功能api接口
1、新建ToDoController.cs继承基础控制器BaseApiController,但是一般业务代码不写在控制器内,业务代码写在Service,先新建统一返回值格式ApiResponse.cs: public class ApiResponse{public ApiResponse(bool status, string mess…...

ffmpeg给视频添加时间水印,准确且不模糊
ffmpeg -i {输入文件路径} -vf{drawtext} {输出文件路径} 针对视频模糊,加上 -b:v {输出视频码率};右键属性,可查看离线视频源码率; 针对离线视频文件加上时间水印,时间跳变不正常,加上-re; 整…...
① vue复习。从安装到使用
vue官网:cn.vuejs.org vue安装 cnpm install -g vue/cli 查看是否安装成功 vue --version 创建一个项目 vue create vue-demo(项目名称) 这个取消掉。空格可选中或者取消。 运行项目: cd 进入到项目下 npm run serve 运行成功后,访问这…...
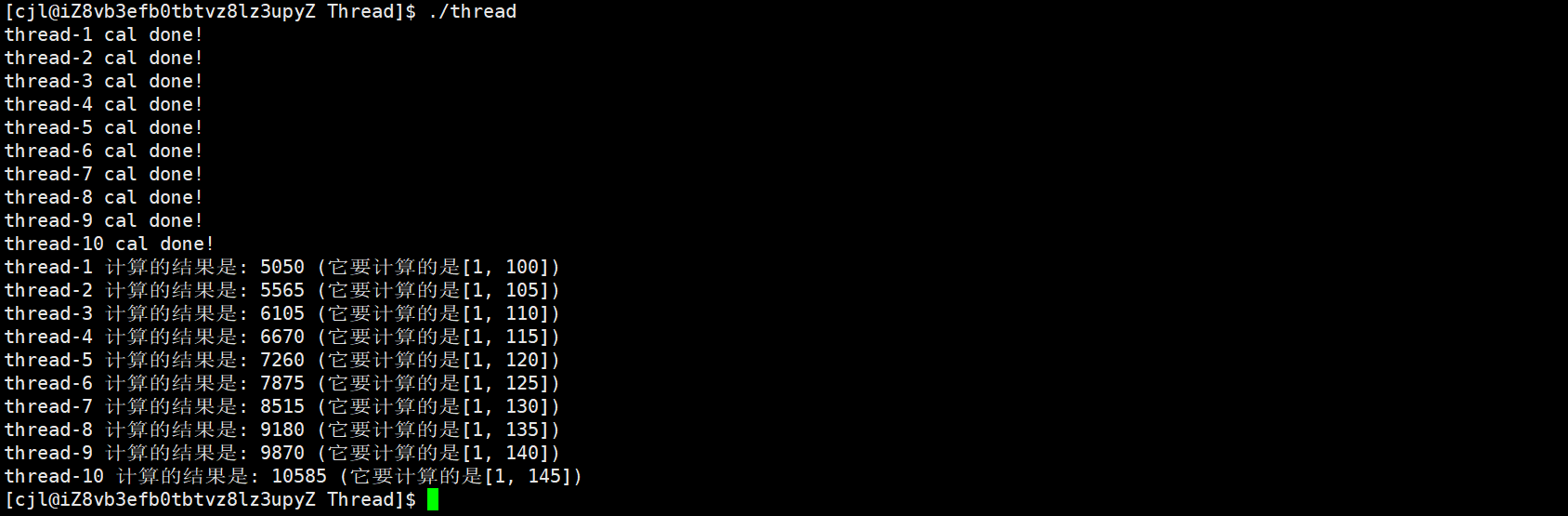
【Linux】多线程——线程引入 | 线程控制
文章目录 一、Linux多线程1. 线程概念2. 线程创建3. 线程和进程4. 线程的优缺点 二、线程控制1. 线程创建2. 线程终止3. 线程等待4. 线程分离5. 线程局部存储 三、线程封装 一、Linux多线程 一级页表和二级页表都是key/val模型,一级页表的key是第一份的10个比特位&a…...
)
查询树形目录(内存遍历成树返回)
实体 Data TableName("dtp_sm_servicetype") ApiModel(value "SmServicetype对象", description "服务类型") EqualsAndHashCode(callSuper true) public class SmServicetype extends BaseEntity {ApiModelProperty("服务类型名称&quo…...
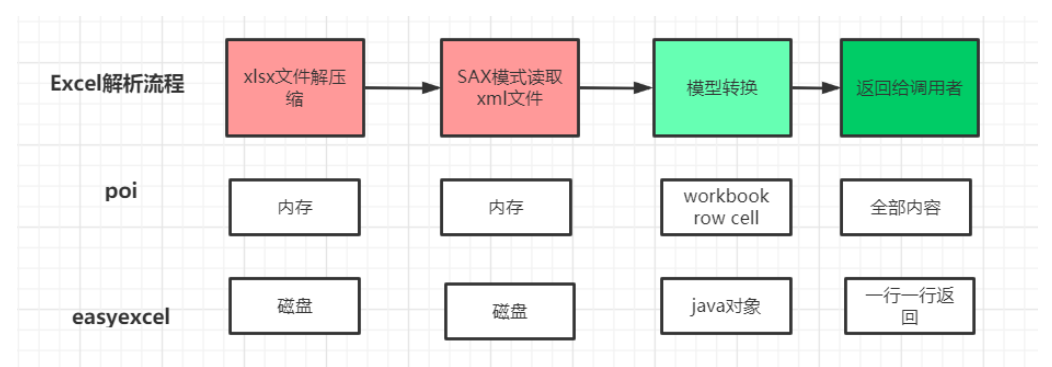
Easys Excel的表格导入(读)导出(写)-----java
一,EasyExcel官网: 可以学习一些新知识: EasyExcel官方文档 - 基于Java的Excel处理工具 | Easy Excel 二,为什么要使用easyexcle excel的一些优点和缺点 java解析excel的框架有很多 : poi jxl,存在问题:非常的消耗内存, easyexcel 我们…...
)
纯净版ISO镜像下载大全(Windows、Linux、mac)
目录 一、前言介绍 前言必读 介绍 二、获取ISO镜像方式 (一)官方镜像下载 (二)获取下载方式 ps:回复的内容都是小写的 Windows操作系统 1.windows XP系统 2.Windows 7系统 3.Windows10系统 4.Windows11系…...

VMware上的Centos设置静态IP
服务器环境一般都是Centos7,而且很多软件在Linux环境上也能支持得更好,所以我需要在本机上使用虚拟机安装Linux,因为需要访问Linux上安装的软件,所以需要固定IP,不然每次更改也不方便。 基础环境准备 安装VMware在VM…...

【MySQL】数据库的基本操作
文章目录 1. 创建数据库1.1 创建数据库的语句1.2 创建一个数据库1.3 查看字符串与校验规则1.4 校验规则对数据库的影响 2. 删除数据库3. 查看数据库4. 修改数据库5. 备份与恢复5.1 数据库的备份与恢复5.2 表的备份与恢复 6. 查看数据库的连接情况 1. 创建数据库 1.1 创建数据库…...

Spring整合MyBatis(详细步骤)
Spring与Mybatis的整合,大体需要做两件事, 第一件事是:Spring要管理MyBatis中的SqlSessionFactory 第二件事是:Spring要管理Mapper接口的扫描 具体的步骤为: 步骤1:项目中导入整合需要的jar包 <dependency><!--Spring操作数据库需要该jar包…...
Linux:Shell编程之正则表达式
目录 绪论 1、正则表达式 1.1 通配符 1.2 正则表达式分类 1.3 基本正则 1.4 正则表达式中表示次数的表达式 1.5 位置锚定 1.5.1 词首锚定和词尾锚定 1.6 分组() 1.7 逻辑或 1.8 扩展正则 绪论 正则表达式:有一类特殊字符以及文本…...
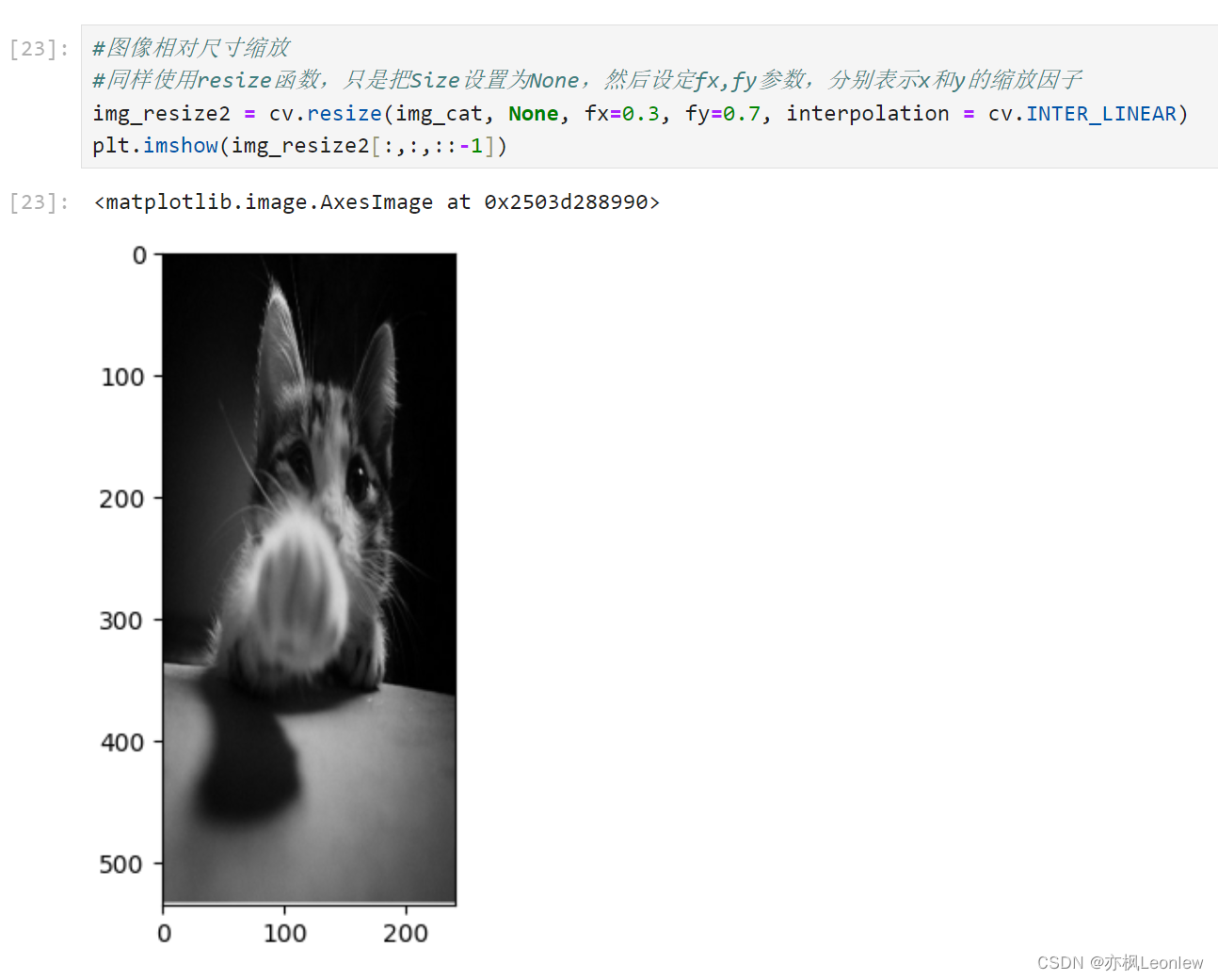
Python Opencv实践 - 图像缩放
import cv2 as cv import numpy as np import matplotlib.pyplot as pltimg_cat cv.imread("../SampleImages/cat.jpg", cv.IMREAD_COLOR) plt.imshow(img_cat[:,:,::-1])#图像绝对尺寸缩放 #cv.resize(src, dsize[, dst[, fx[, fy[, interpolation]]]]) #指定Size大…...

大脑营行|“福安市华龙教育基金”支持家乡教育事业发展
8月8日,福安市松罗中学举行“福安市华龙教育基金”中考奖学金颁发仪式。福安市松罗乡党委书记钟文、乡长郑仁寿、福安市人民政府教育督导室副科级督导员(片区领导)陈秦、校长张明亮、各村支部书记、家长代表、受奖学生,校领导班子…...

Windows 2016安装Jenkins
Jenkins 下载,安装 下载OpenJDK 11 for Wndows 两种方式 choco install openjdk11 https://github.com/adoptium/temurin11-binaries/releases/download/jdk-11.0.20%2B8/OpenJDK11U-jdk_x64_windows_hotspot_11.0.20_8.msi how to enable administrator user to …...

章节4:Burp Target模块
章节4:Burp Target模块 Burp渗透测试流程 01 Target模块的作用 与HTTP History的区别 HTTP History按时间顺序记录Target按主机或者域名分类记录(字母顺序) Target模块的作用 把握网站的整体情况对一次工作的域进行分析分析网站存在的攻…...
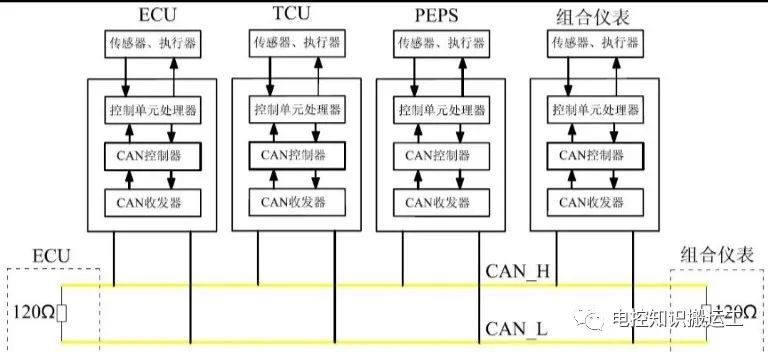
CAN总线一些经典的现场故障
本文分析一些经典的CAN总线现场故障。 1、CAN总线的常见故障 CAN总线错误分析与解决 当CAN总线出现故障或数据传输异常时,往往会出现多种奇怪的故障现象,如仪表板显示异常,车辆无法启动,启动后无法熄灭,车辆动力性能下降,某些电控系统功能失等。 这是因为相关数据或信息…...

VS+QT+Opencv使用YOLOv4对视频流进行目标检测
对单张图像的检测,请参考:https://blog.csdn.net/qq_45445740/article/details/109659938 #include <fstream> #include <sstream> #include <iostream> #include <opencv2/dnn.hpp> #include <opencv2/imgproc.hpp> #inc…...

第19节 Node.js Express 框架
Express 是一个为Node.js设计的web开发框架,它基于nodejs平台。 Express 简介 Express是一个简洁而灵活的node.js Web应用框架, 提供了一系列强大特性帮助你创建各种Web应用,和丰富的HTTP工具。 使用Express可以快速地搭建一个完整功能的网站。 Expre…...

(二)TensorRT-LLM | 模型导出(v0.20.0rc3)
0. 概述 上一节 对安装和使用有个基本介绍。根据这个 issue 的描述,后续 TensorRT-LLM 团队可能更专注于更新和维护 pytorch backend。但 tensorrt backend 作为先前一直开发的工作,其中包含了大量可以学习的地方。本文主要看看它导出模型的部分&#x…...

【单片机期末】单片机系统设计
主要内容:系统状态机,系统时基,系统需求分析,系统构建,系统状态流图 一、题目要求 二、绘制系统状态流图 题目:根据上述描述绘制系统状态流图,注明状态转移条件及方向。 三、利用定时器产生时…...

【C语言练习】080. 使用C语言实现简单的数据库操作
080. 使用C语言实现简单的数据库操作 080. 使用C语言实现简单的数据库操作使用原生APIODBC接口第三方库ORM框架文件模拟1. 安装SQLite2. 示例代码:使用SQLite创建数据库、表和插入数据3. 编译和运行4. 示例运行输出:5. 注意事项6. 总结080. 使用C语言实现简单的数据库操作 在…...
)
Java入门学习详细版(一)
大家好,Java 学习是一个系统学习的过程,核心原则就是“理论 实践 坚持”,并且需循序渐进,不可过于着急,本篇文章推出的这份详细入门学习资料将带大家从零基础开始,逐步掌握 Java 的核心概念和编程技能。 …...

Java线上CPU飙高问题排查全指南
一、引言 在Java应用的线上运行环境中,CPU飙高是一个常见且棘手的性能问题。当系统出现CPU飙高时,通常会导致应用响应缓慢,甚至服务不可用,严重影响用户体验和业务运行。因此,掌握一套科学有效的CPU飙高问题排查方法&…...

站群服务器的应用场景都有哪些?
站群服务器主要是为了多个网站的托管和管理所设计的,可以通过集中管理和高效资源的分配,来支持多个独立的网站同时运行,让每一个网站都可以分配到独立的IP地址,避免出现IP关联的风险,用户还可以通过控制面板进行管理功…...

C++ 设计模式 《小明的奶茶加料风波》
👨🎓 模式名称:装饰器模式(Decorator Pattern) 👦 小明最近上线了校园奶茶配送功能,业务火爆,大家都在加料: 有的同学要加波霸 🟤,有的要加椰果…...

计算机基础知识解析:从应用到架构的全面拆解
目录 前言 1、 计算机的应用领域:无处不在的数字助手 2、 计算机的进化史:从算盘到量子计算 3、计算机的分类:不止 “台式机和笔记本” 4、计算机的组件:硬件与软件的协同 4.1 硬件:五大核心部件 4.2 软件&#…...

前端中slice和splic的区别
1. slice slice 用于从数组中提取一部分元素,返回一个新的数组。 特点: 不修改原数组:slice 不会改变原数组,而是返回一个新的数组。提取数组的部分:slice 会根据指定的开始索引和结束索引提取数组的一部分。不包含…...
