CSDN竞赛70期
CSDN竞赛70期
- CSDN竞赛70期
- 1.小张的手速大比拼
- 分析
- 代码
- 2.坐公交
- 分析
- 代码
- 3.三而竭
- 分析
- 代码
- 4.争风吃醋的豚鼠
- 分析
- 代码
CSDN竞赛70期
1.小张的手速大比拼
在很久很久以前,小张找到了一颗有 N 个节点的有根树 T 。 树上的节点编号在 1 到 N 范围内。 他很快发现树上的每个节点 i 都有一个对应的整数值 V[i]。 一个老爷爷对他说,给你一个整数 X, 如果你能回答我的 M 个问题,他就给张浩扬购买一些零食。 对于每个问题 Q[i], 请你找到 在 T 中以节点 Q[i] 为根的子树中的所有节点(包括 Q[i])中, 有没有两个节点 A, B (A != B) 的值 V[A] ^ V[B] 的异或和为 X。 如果有这样的两个节点, 请你输出 YES。 否则你需要输出 NO 表示
没有节点符合上面的条件。
分析
这一题有点复杂,考试的时候考虑复杂性,先做了后面的题,之后没时间做了。赛后搜了一下,也没解决方案。这次的前10名也没有谁给出了代码,所以我说一下自己的思考
为了能够满足题目的时间复杂度要求,要先计算出每个节点为根的树是否存在A^B=X.
要从后向前计算,如果节点i为根的子树中存在,那么i的父节点也存在,如果不存在,就要计算树中是否存在。
假设有节点i,dp[i]表示是否存在这样的节点A和B,i有两个子节点i1和i2,如果dp[i1]或者dp[i2]是true,那么dp[i]就是true,否则就需要计算
如何计算树中是否存在A,B呢?我一看到异或就想到异或相关的规律,比如aa=0,a0=a,a^-1=~a,想着找一找异或的特殊性,但是这些好像都用不上,那只能用笨办法了,遍历所有的结点,两两异或计算是否等于X。如果dp[i1]和dp[i2]都是false,就不要在i1和i2的子树内部找了,只需要找节点i和i1子树,节点i和i2子树,i1子树中的节点和i2子树的结点。输入的数据有两个数组,数组N表示节点的父节点,数组V表示节点的值,这样的输入比较方便查找每个节点的父节点,但是不好查找子节点,在计算的时候是需要不断的找子节点的,如果每次都需要遍历数组N,那肯定有很多次的重复查找,比如说计算dp[i]的时候需要找子节点i1和i2,计算i父节点的时候可能还要找i1和i2,中间的重复是很多的,因为每个节点的子节点一定是相邻的,所以需要再定义一个数组Firstchild来存放每个节点的第一个子节点的位置,其他的子节点都在这个节点的相邻后面,这样在查找子节点的时候不用每次都遍历数组N了。我在写代码的时候又想到,因为是从后向前计算dp,不需要知道父节点,只需要知道子节点就行了,所以可以直接定义一个child[n][2]数组,child[n][0]表示第一个子节点,child[n][1]表示最后一个子节点(代码中为了好写代码,表示的是最后一个子节点编号+1)
其实最开始的时候我想过根据N和V来创建一个链表结构的多叉树,后来想想也挺麻烦的,不如直接多加一个数组Firstchild。
下面是我的代码,注意:代码是后来写的,没有经过平台的测试,不能保证一定正确。如果代码有不对的地方,欢迎在评论区指正。
写完代码和测试之后,我又想可能不需要求出每个节点的dp[i],只需要求出大于等于Q中最小值的dp[i],小于i(i的父节点)的节点没被要求计算,不用计算。
代码
#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>// // 计算树中是否有节点和i的异或和为x
bool vi_exor_tree_equal_x(int vi, int child[][2], int V[], int tree_num, int x)
{// printf("vi=%d,V[%d]=%d,x=%d\n",vi,tree_num,V[tree_num],x);if ((vi ^ V[tree_num]) == x) // i和i的子节点异或是否为xreturn true;else{// i和i子节点的子节点异或if (child[tree_num][0] == -1) // i的子节点没有子节点return false;else{for (int j = child[tree_num][0]; j < child[tree_num][1]; j++){if (vi_exor_tree_equal_x(vi, child,V,j,x))return true;}return false;}}
}bool tree1_exor_tree2_equal_x(int child[][2], int V[], int num1, int num2, int x)
{// tree1的根节点和tree2整个树异或if (vi_exor_tree_equal_x(V[num1],child,V,num2,x))return true;// tree1的所有节点依次和tree2整个树异或if (child[num1][0] != -1){for (int i = child[num1][0]; i < child[num1][1]; i++){if (vi_exor_tree_equal_x(V[i],child,V,num2,x))return true;}}return false;
}void calculate_dp(int child[][2], int V[], int n, int x, bool dp[])
{for (int i = n-1; i >= 0; i--){if (child[i][0] == -1) // 没有子节点dp[i] = false;else // 有子节点{// 遍历每个子节点int j = child[i][0]; // i的第一个子节点while (j < child[i][1] && dp[j] == false) // j的父节点是ij++;if (j < child[i][1] && dp[j]) // 有子节点是truedp[i] = true;else{dp[i] = false; // 先设置为false// 计算子树中是否有节点和i的异或和为xfor (int k = child[i][0]; k < child[i][1]; k++){if (vi_exor_tree_equal_x(V[i],child,V,k,x)){dp[i] = true;break;}}if (dp[i]){continue;// printf("1-dp[%d]=%d\n",i,dp[i]);}// 子树与子树之间是否有节点异或和为xfor (int k = child[i][0]; k < child[i][1]; k++){for (int m = k+1; m < child[i][1]; m++){if (tree1_exor_tree2_equal_x(child, V, k, m, x)){dp[i] = true;break;}}}// printf("2-dp[%d]=%d\n",i,dp[i]);}}// printf("3-dp[%d]=%d\n",i,dp[i]);}
}int main()
{int n, x, m;scanf("%d %d %d",&n, &x, &m);int parent[n], child[n][2], V[n], Q[m];bool dp[n];for (int i = 0; i < n; i++){scanf("%d", &parent[i]);}for (int i = 0; i < n; i++){scanf("%d", &V[i]);}for (int i = 0; i < m; i++){scanf("%d", &Q[i]);}// 计算childfor (int i = 0; i < n; i++){int j = i+1; // 子节点一定在父节点的右边while (j < n && parent[j] < (i+1)) // 输入的树编号是从1开始的j++;if (j < n && parent[j] == (i+1)){child[i][0] = j;while (j < n && parent[j] == (i+1))j++;child[i][1] = j;}elsechild[i][0] = -1; // 没有子节点}// printf("child0:\n");// for (int i = 0; i < n; i++)// {// printf("%d ",child[i][0]);// }// printf("\n");// printf("child1:\n");// for (int i = 0; i < n; i++)// {// printf("%d ",child[i][1]);// }// printf("\n");calculate_dp(child,V,n,x,dp);for (int i = 0; i < m; i++){printf("%s\n",dp[Q[i]-1]? "YES" : "NO");}
}
测试用例:
6 3 6
-1 1 1 2 2 3
5 1 4 3 0 8
6 5 4 3 2 1
NO
NO
NO
NO
YES
YES
6 3 3
-1 1 1 2 2 3
5 1 4 8 0 3
3 2 1
NO
NO
YES
2.坐公交
公交上有N排凳子,每排有两个凳子,每一排的凳子宽度不一样。有一些内向和外向的人按照顺序上车。
外向的人(0):只会选择没人的一排坐下,如果有很多排符合要求,他会选择座位宽度最小的坐下。
内向的人(1):只会选择有人的一排坐下,如果有很多排符合要求,他会选择座位宽度最大的坐下。
数据保证存在合理。输出每个人所在的排。
分析
内向的人和外向的人的行为完全相反,对外向的人的座位做入栈操作,对内向的人做出栈操作。首先以宽度来对座位进行排序,外向的人选择没人且宽度最小的座位,第一个外向的人选择最小的座位,第二个外向的人选择第二小的座位,……。对于内向的人选择有人且宽度最大的座位,入栈的时候代表有人坐,且先入栈的宽度肯定小于后入栈的宽度,所以内向的人直接做出栈操作就可以了。
这题需要排序,排序算法有很多,最简单的是冒泡排序,但冒泡排序的时间复杂度是O(n^2),肯定会超时,我是使用的快速排序,时间复杂度O(nlog(n)),但是快速排序是不稳定的排序,如果遇到相同的值,有可能导致顺序调换,但是题目中没有说有宽度相同的情况。还有一个归并排序,时间复杂度和快速排序相同,而且是稳定的,只是忘了怎么写了。
这一题我得了0分,很奇怪,测试用例是没问题的,而且我自己试了很多例子也没问题,但是执行代码,通过率是0。即使是使用了不稳定的快速排序,也不可能一个测试用例都没过吧,我怀疑是数据输入的格式问题,考试时,已经给我了获取输入的代码,但是代码都是错的。
代码
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#define MIN(x,y) ((x)<(y)? (x):(y))
void swap(int *a, int *b)
{int t = *a;*a = *b;*b = t;
}
void quick_sort(int a[], int l, int r, int seq[])
{if (l >= r)return;int i = l - 1;int j = r + 1;int base = a[(i+j)/2];while(i < j) {do i++;while(a[i] < base);do j--;while(a[j] > base);if (i < j) {swap(&a[i],&a[j]);swap(&seq[i],&seq[j]);}}quick_sort(a,l,j,seq);quick_sort(a,j+1,r,seq);
}void solution(int n, int arr[], char *personality)
{//char flag[n] = {0};char z[n]; // 栈int top = 0;int seq[n];for (int i = 0; i < n; i++) {seq[i] = i;}quick_sort(arr,0,n-1,seq);int count = 0;for (int i = 0; i < 2*n; i++) {if (personality[i] == '0') {int num = seq[count++]+1;printf("%d",num);z[top++] = num;} else {printf("%d",z[--top]);}if (i != 2*n-1)printf(" ");}// printf("\n");
}
int main()
{int n;scanf("%d", &n);int* arr;arr = (int*)malloc(n * sizeof(int));for (int i = 0; i < n; i++) {scanf("%d", &arr[i]);}char *personality = (char *)malloc(2*n+1);scanf("%s", personality);// printf("%s",personality);//printf("\n");solution(n, arr, personality);return 0;
}
3.三而竭
一鼓作气再而衰三而竭。 小艺总是喜欢把任务分开做。 小艺接到一个任务,任务的总任务量是n。 第一天小艺能完成x份任务。 第二天能完成x/k。 。。。 第t天能完成x/(k^(t-1))。 小艺想知道自己第一天至少完成多少才能完成最后的任务。
分析
等比数列求和公式:sum = x*(1-(1/k)^t)/(1-1/k)
x*(1-(1/k)^t)/(1-1/k) >= n
x >= n*(1-1/k) / (1 -(1/k)^t)
当t趋向于无穷大的时候,
x >= n*(1-1/k)
但是,因为每天完成的工作量不能是小数,所以直接用n*(1-1/k)求出来的值肯定是会小于真实值的。
所以,把n*(1-1/k)作为最小值,然后递增,判断是否能完成任务。其实还有一个问题,就是真实的值和n*(1-1/k)到底相差多少呢?如果差的太多,查找起来也会比较慢,所以想到二分查找,x可取的最大值是n(第一天就完成了),最小值是n*(1-1/k),二分查找,知道找到满足条件的最小值。
我使用的第一种方法,能够AC。
代码
#include <stdio.h>
#include <string.h>
#include <stdbool.h>
#include <time.h>#define IS_INT(x) ((x)-(int)(x) < 1e-7)
#define MAX(x,y) ((x)>(y)? (x):(y))int main()
{int n, k;int min, max;scanf("%d %d",&n, &k);// clock_t start = clock();double t = n*(1-1.0/k);if (IS_INT(t))min = t;elsemin = t+1;while(1){int sum = 0;int work = min; // 当天的工作量while(sum < n && work > 0){sum += work;work = work / k;}if (sum >= n)break;elsemin++;}printf("%d\n",min);// clock_t end = clock();// printf("time:%lu\n",end-start);
}
4.争风吃醋的豚鼠
N个节点两两建边。 不存在3个节点相互之前全部相连。(3个节点连接成环) 最多能建立多少条边?
分析
这一题是通过找规律来计算出来的
f(1) = 0
f(2) = 1
f(3) = 2
f(4) = 4
f(5) = 6
f(6) = 9
于是我总结出:
f(n) = f(n-1) + n/2
我是当成了动态规划来解的。
后来看别人的代码,发现:
f(n) = (n + 1)/2 * (n /2)
我会总结成f(n) = f(n-1) + n/2是因为我是通过画图,每多加一个节点,是在前面的基础上增加x个边,我是在总结这个x。如果对数字更敏感的话,应该就能总结出f(n) = (n + 1)/2 * (n /2)了。
代码
#include <stdio.h>
#include <stdlib.h>void solution(int n)
{if(n == 1) {printf("0");return;}long dp_1 = 0; // f(n-1),f(1)long dp; // f(n)int i = 2;while (i <= n) {dp = dp_1 + i/2;dp_1 = dp;i++;}printf("%ld",dp);
}int main()
{int n;scanf("%d", &n);solution(n);return 0;
}
相关文章:

CSDN竞赛70期
CSDN竞赛70期 CSDN竞赛70期1.小张的手速大比拼分析代码 2.坐公交分析代码 3.三而竭分析代码 4.争风吃醋的豚鼠分析代码 CSDN竞赛70期 1.小张的手速大比拼 在很久很久以前,小张找到了一颗有 N 个节点的有根树 T 。 树上的节点编号在 1 到 N 范围内。 他很快发现树上…...
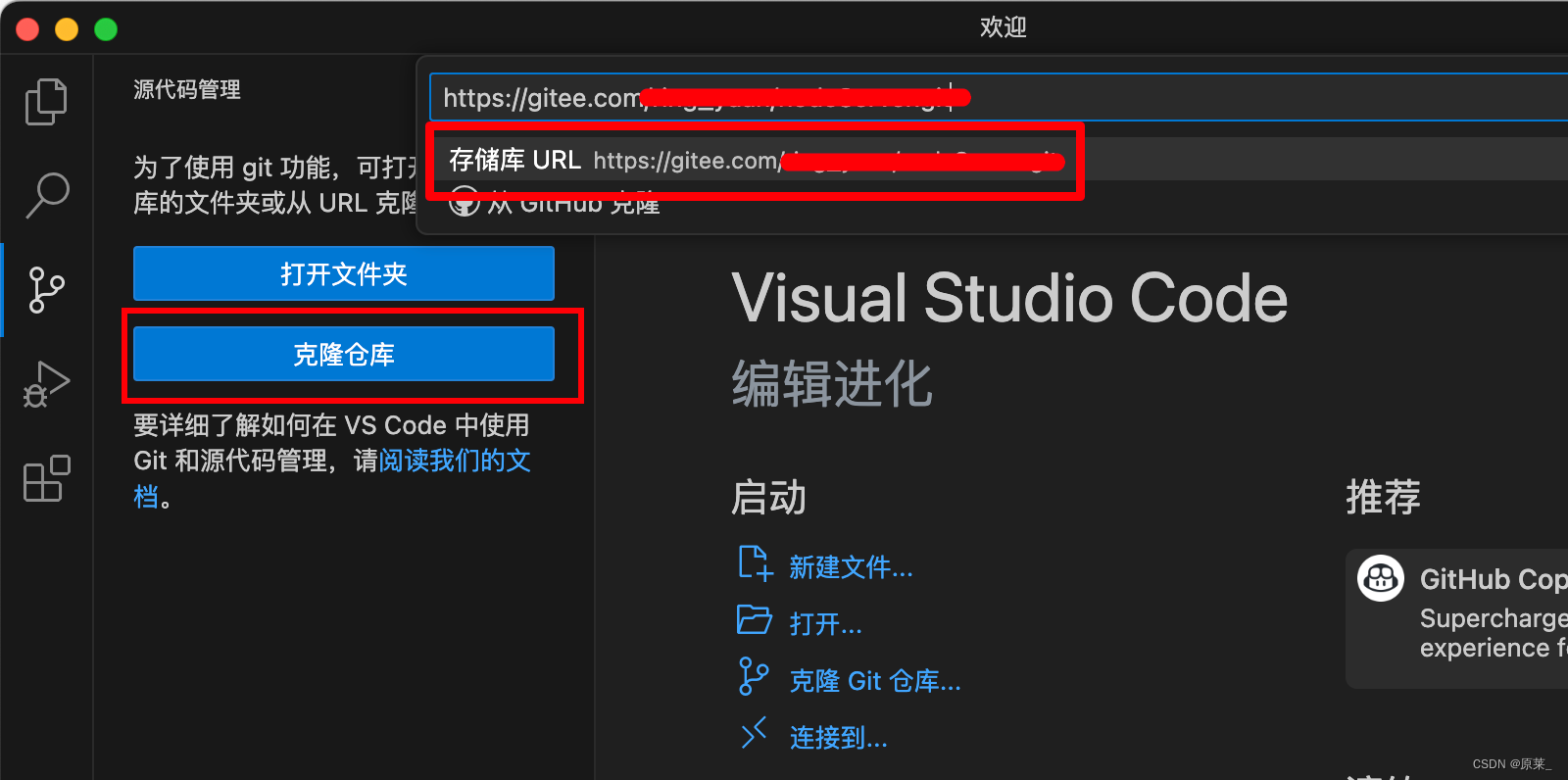
mac安装vscode 配置git
1、安装vscode 官网地址 下载mac稳定版安装很慢的解决办法 (转自) mac电脑如何解决下载vscode慢的问题 选择谷歌浏览器右上角的3个点,选择下载内容,右键选择复制链接地址,在新窗口粘贴地址, 把地址中的一段替换成下面的vscode.cd…...
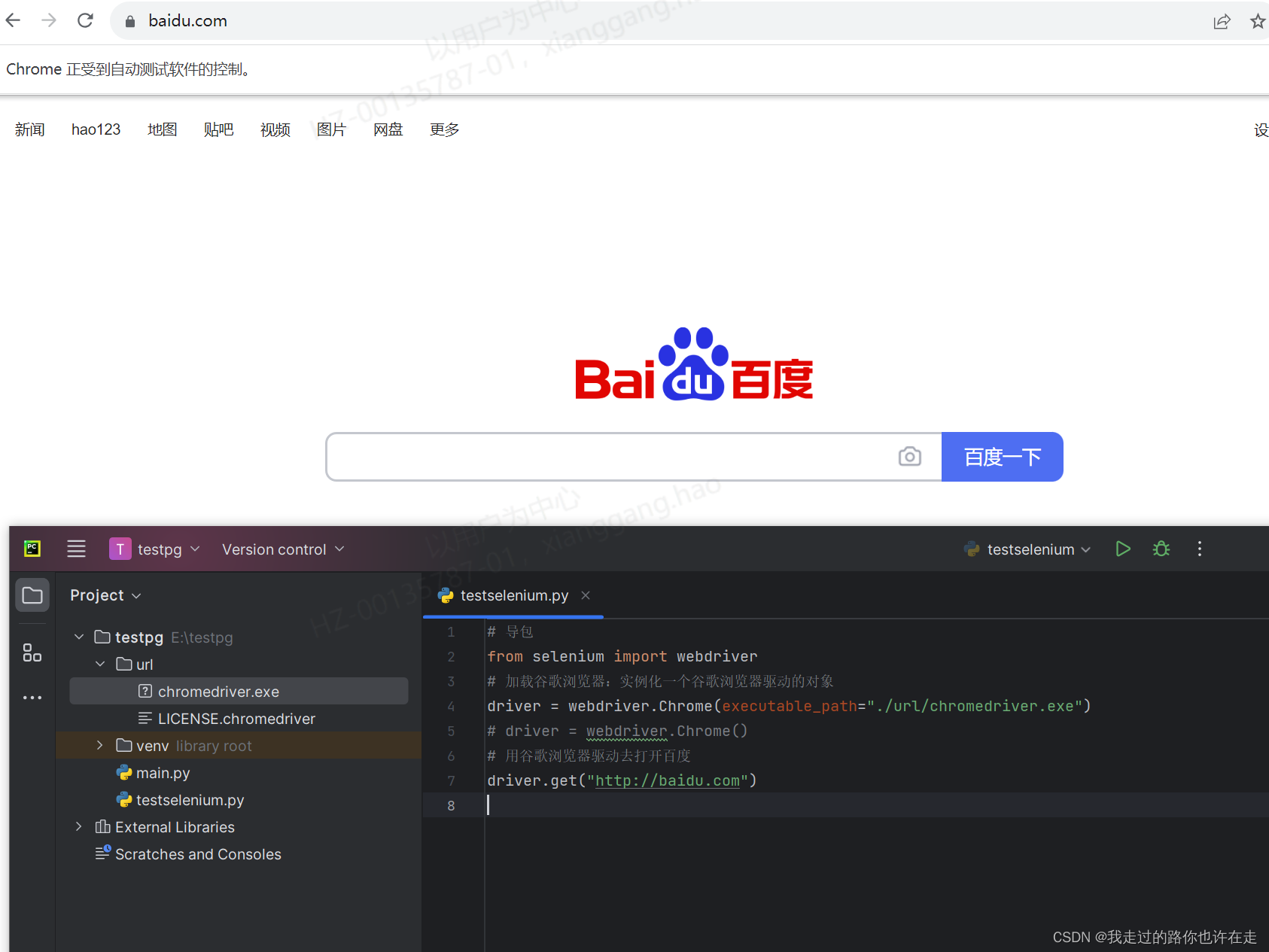
UI自动化环境的搭建(python+pycharm+selenium+chrome)
最近在做一些UI自动化的项目,为此从环境搭建来从0到1,希望能够帮助到你,同时也是自我的梳理。将按照如下进行开展: 1、python的下载、安装,python环境变量的配置。 2、pycharm开发工具的下载安装。 3、selenium的安装。…...
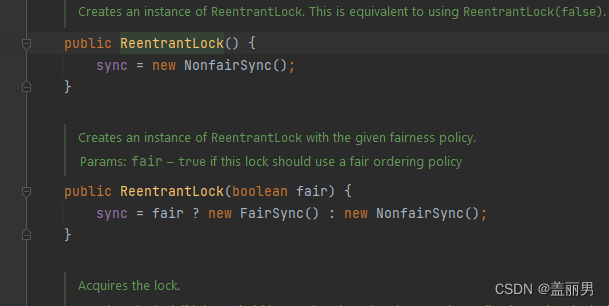
AbstractQueuedSynchronizer
目录 AQS是什么AQS什么样内部类成员变量方法public如果不使用AQS会怎样 AQS的应用ReentrantLockSyncNonfairSyncFairSync 其他实现 AQS是什么 AbstractQueuedSynchronizer(AQS)是Java中的一个并发工具,位于java.util.concurrent.locks包中&a…...

谈谈什么是云计算?以及它的应用
作者:Insist-- 个人主页:insist--个人主页 作者会持续更新网络知识和python基础知识,期待你的关注 目录 编辑 一、什么是云计算 二、云计算的优势与劣势? 1、云计算的优势 ①提高资源利用率 ②提升效率 ③降低成本 2、云…...
)
【BASH】回顾与知识点梳理(十六)
【BASH】回顾与知识点梳理 十六 十六. 十二至十五章知识点总结及练习16.1 总结16.2 练习16.3 简答题 该系列目录 --> 【BASH】回顾与知识点梳理(目录) 十六. 十二至十五章知识点总结及练习 16.1 总结 绝对路径:『一定由根目录 / 写起』…...
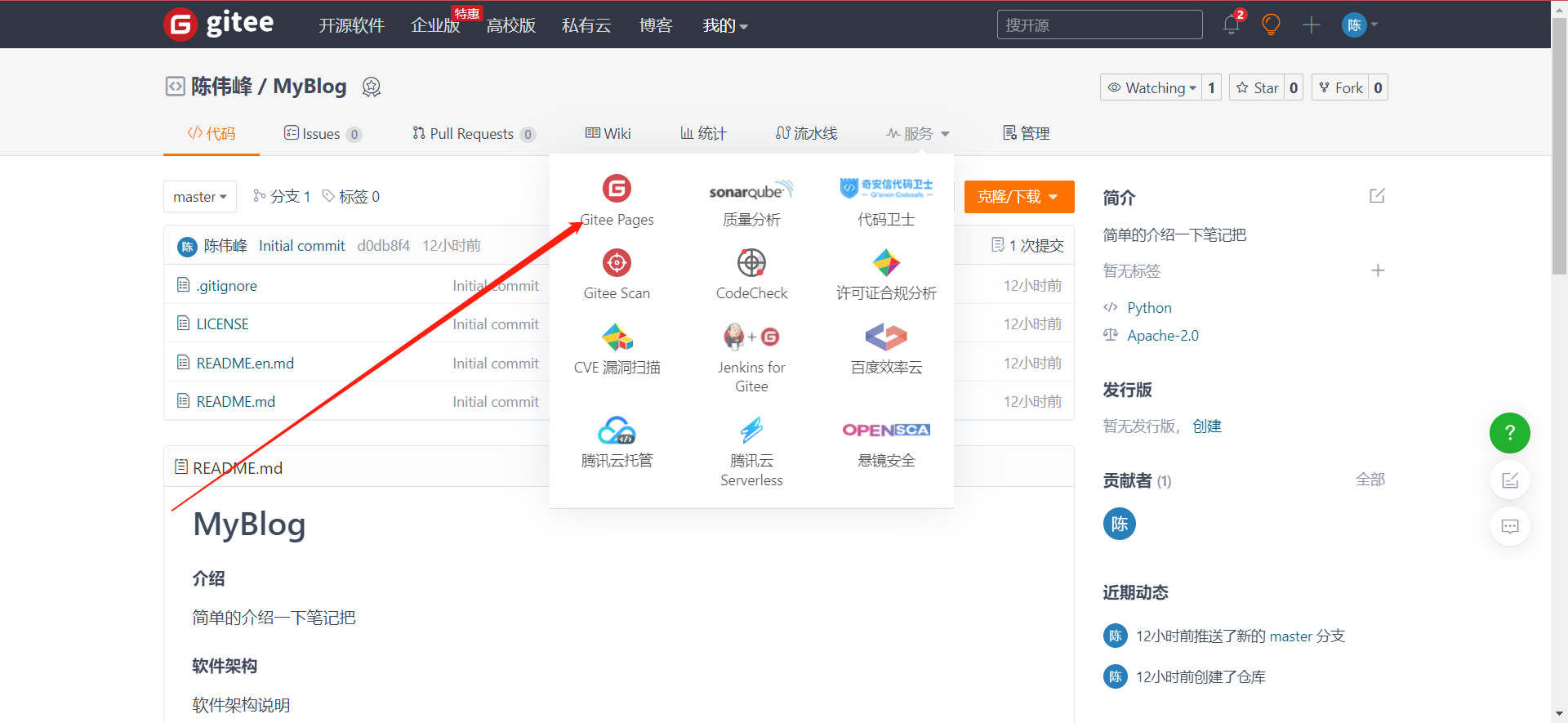
docsify gitee 搭建个人博客
docsify & gitee 搭建个人博客 文章目录 docsify & gitee 搭建个人博客1.npm 安装1.1 在Windows上安装npm:1.2 在macOS上安装npm:1.3 linux 安装npm 2. docsify2.1 安装docsify2.2 自定义配置2.2.1 通过修改index.html,定制化开发页面…...

SpringBoot2-Tomcat部署
1.排除内置 Tomcat 在pom.xml文件中的下添加以下代码,用于排除SpringBoot内置Tomcat <dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-web</artifactId><exclusions><exclusion&…...

Docker查看、创建、进入容器相关的命令
1.查看、创建、进入容器的指令 用-it指令创建出来的容器,创建完成之后会立马进入容器。退出之后立马关闭容器。 docker run -it --namec1 centos:7 /bin/bash退出容器: exit查看现在正在运行的容器命令: docker ps查看历史容器࿰…...

leetcode1. 两数之和
题目:leetcode1. 两数之和 描述: 给定一个整数数组 nums 和一个整数目标值 target,请你在该数组中找出 和为目标值 target 的那 两个 整数,并返回它们的数组下标。 你可以假设每种输入只会对应一个答案。但是,数组中…...
温室花卉种植系统springboot框架jsp鲜花养殖智能管理java源代码
本项目为前几天收费帮学妹做的一个项目,Java EE JSP项目,在工作环境中基本使用不到,但是很多学校把这个当作编程入门的项目来做,故分享出本项目供初学者参考。 一、项目描述 基于Git无线传感网络的温室花卉种植智能控制系统 系统…...
测试老鸟经验总结,Jmeter性能测试-重要指标与性能结果分析(超细)
目录:导读 前言一、Python编程入门到精通二、接口自动化项目实战三、Web自动化项目实战四、App自动化项目实战五、一线大厂简历六、测试开发DevOps体系七、常用自动化测试工具八、JMeter性能测试九、总结(尾部小惊喜) 前言 Aggregate Report …...
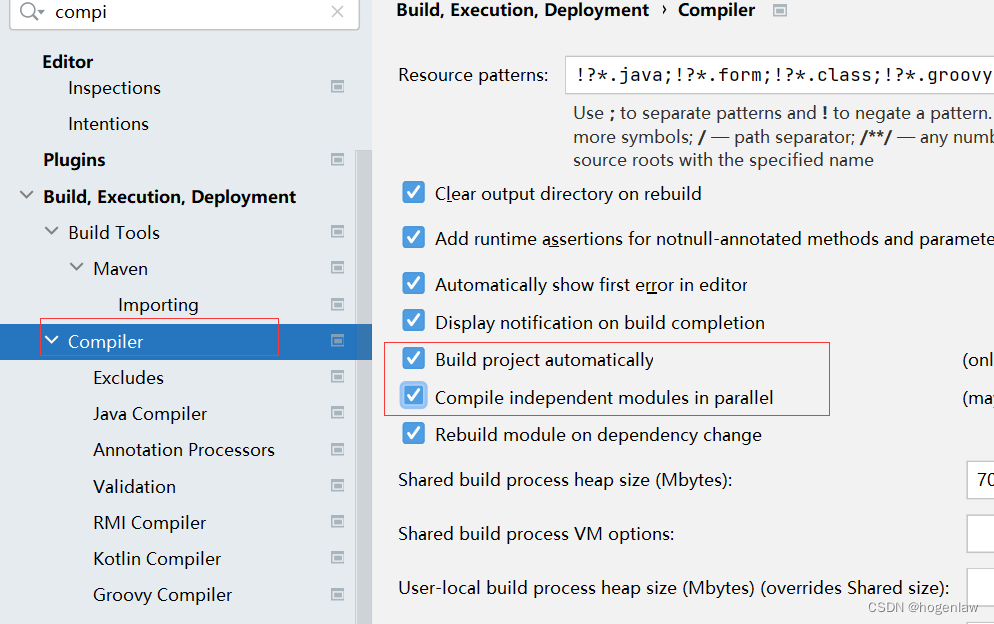
IDEA设置Maven自动编译model
IDEA设置Maven自动编译model 项目工程结构IDEA maven设置 项目工程结构 假设我们的项目结构是下图这样,也就是一个父工程下包含多个子模块,其中dubbo-01-api是公共模块,其它两个模块要想使用必须在pom文件中引入。 本地开发要想不会报错&am…...

关于本地mockjs的使用
安装mockjs npm install mockjs -s在src下新建目录mockData,所有mock请求可以放该文件夹下面。例如在mockData文件夹下新建一个home.js文件。用来处理首页的请求数据 home.js export default {getHomeData:()>{return{code:200,data:{tableData:[{name:张三,se…...

hive 中最常用日期处理函数
hive 常用日期处理函数 在工作中,日期函数是提取数据计算数据必须要用到的环节。哪怕是提取某个时间段下的明细数据也得用到日期函数。今天和大家分享一下常用的日期函数。为什么说常用呢?其实这些函数在数据运营同学手上是几乎每天都在使用的。 技术交…...
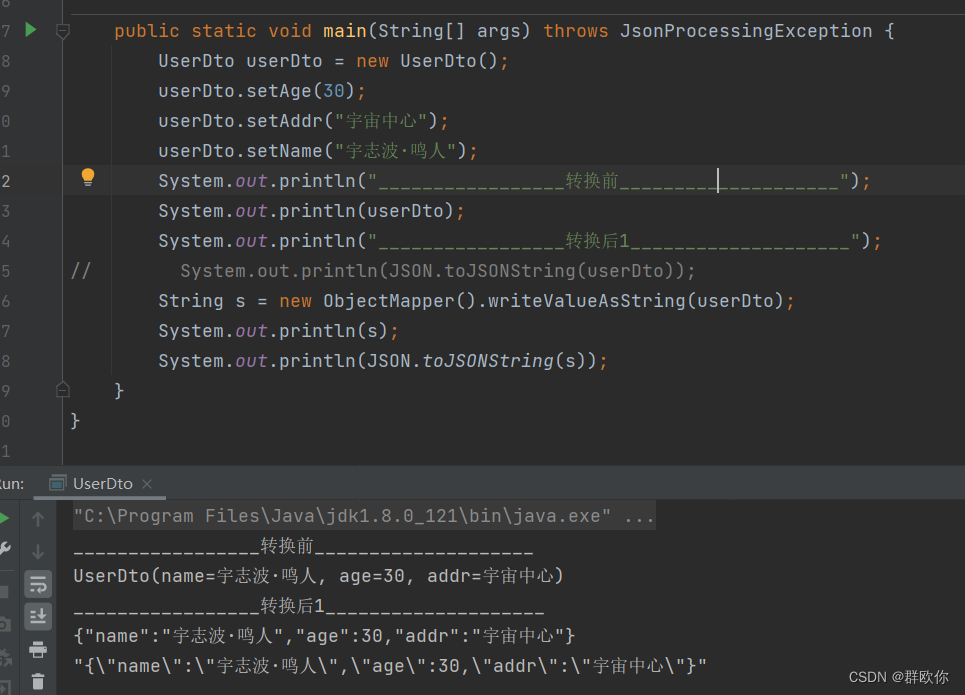
记录一下Java实体转json字段顺序问题
特殊需求,和C交互他们那边要求字段顺序要和他们定义的一致(批框架) 如下: Data public class UserDto {private String name;private Integer age;private String addr; }未转换前打印: 转换后打印: 可以看到转换为json顺序打印…...
)
微积分入门:总结归纳汇总(一)
基础 标准符号约定: ( s i n x ) n (sinx)^n (sinx)...

ubuntu python虚拟环境venv搭配systemd服务实战(禁用缓存下载--no-cache-dir)
文章目录 参考文章目录结构步骤安装venv查看python版本创建虚拟环境激活虚拟环境运行我们程序看缺少哪些依赖库,依次安装它们接下来我们配置python程序启动脚本,脚本中启动python程序前需先激活虚拟环境配置.service文件然后执行部署脚本,成功…...

案例15 Spring Boot入门案例
1. 选择Spring Initializr快速构建项目 2. 设置项目信息 3. 选择依赖 4. 设置项目名称 5. 项目结构 6. 项目依赖 自动配置了Spring MVC、内置了Tomcat、配置了Logback(日志)、配置了JSON。 7. 创建HelloController类 com.wfit.boot.hello目录下创建HelloCo…...

物联网是下一个风口吗?
随着科技的持续进步,物联网行业正在迅速兴起,展现出巨大的潜力。那么,物联网行业的未来是什么样的呢? 1. 5G技术的广泛应用和普及 随着5G技术的快速发展和商业化推广,物联网行业将迎来一个巨大的飞跃。5G技术的高速传…...

逻辑回归:给不确定性划界的分类大师
想象你是一名医生。面对患者的检查报告(肿瘤大小、血液指标),你需要做出一个**决定性判断**:恶性还是良性?这种“非黑即白”的抉择,正是**逻辑回归(Logistic Regression)** 的战场&a…...

Docker 运行 Kafka 带 SASL 认证教程
Docker 运行 Kafka 带 SASL 认证教程 Docker 运行 Kafka 带 SASL 认证教程一、说明二、环境准备三、编写 Docker Compose 和 jaas文件docker-compose.yml代码说明:server_jaas.conf 四、启动服务五、验证服务六、连接kafka服务七、总结 Docker 运行 Kafka 带 SASL 认…...

Auto-Coder使用GPT-4o完成:在用TabPFN这个模型构建一个预测未来3天涨跌的分类任务
通过akshare库,获取股票数据,并生成TabPFN这个模型 可以识别、处理的格式,写一个完整的预处理示例,并构建一个预测未来 3 天股价涨跌的分类任务 用TabPFN这个模型构建一个预测未来 3 天股价涨跌的分类任务,进行预测并输…...

家政维修平台实战20:权限设计
目录 1 获取工人信息2 搭建工人入口3 权限判断总结 目前我们已经搭建好了基础的用户体系,主要是分成几个表,用户表我们是记录用户的基础信息,包括手机、昵称、头像。而工人和员工各有各的表。那么就有一个问题,不同的角色…...
:滤镜命令)
ffmpeg(四):滤镜命令
FFmpeg 的滤镜命令是用于音视频处理中的强大工具,可以完成剪裁、缩放、加水印、调色、合成、旋转、模糊、叠加字幕等复杂的操作。其核心语法格式一般如下: ffmpeg -i input.mp4 -vf "滤镜参数" output.mp4或者带音频滤镜: ffmpeg…...

反射获取方法和属性
Java反射获取方法 在Java中,反射(Reflection)是一种强大的机制,允许程序在运行时访问和操作类的内部属性和方法。通过反射,可以动态地创建对象、调用方法、改变属性值,这在很多Java框架中如Spring和Hiberna…...

数据库分批入库
今天在工作中,遇到一个问题,就是分批查询的时候,由于批次过大导致出现了一些问题,一下是问题描述和解决方案: 示例: // 假设已有数据列表 dataList 和 PreparedStatement pstmt int batchSize 1000; // …...

【Java学习笔记】BigInteger 和 BigDecimal 类
BigInteger 和 BigDecimal 类 二者共有的常见方法 方法功能add加subtract减multiply乘divide除 注意点:传参类型必须是类对象 一、BigInteger 1. 作用:适合保存比较大的整型数 2. 使用说明 创建BigInteger对象 传入字符串 3. 代码示例 import j…...

sipsak:SIP瑞士军刀!全参数详细教程!Kali Linux教程!
简介 sipsak 是一个面向会话初始协议 (SIP) 应用程序开发人员和管理员的小型命令行工具。它可以用于对 SIP 应用程序和设备进行一些简单的测试。 sipsak 是一款 SIP 压力和诊断实用程序。它通过 sip-uri 向服务器发送 SIP 请求,并检查收到的响应。它以以下模式之一…...

DingDing机器人群消息推送
文章目录 1 新建机器人2 API文档说明3 代码编写 1 新建机器人 点击群设置 下滑到群管理的机器人,点击进入 添加机器人 选择自定义Webhook服务 点击添加 设置安全设置,详见说明文档 成功后,记录Webhook 2 API文档说明 点击设置说明 查看自…...
