题目:2511.最多可以摧毁的敌人城堡数量
题目来源:
leetcode题目,网址:2511. 最多可以摧毁的敌人城堡数目 - 力扣(LeetCode)
解题思路:
顺序遍历数组,记录上一个我军城堡和没有城堡的位置。当碰到空位置时,若上一次更新的值为我军城堡,记录较大的摧毁数;当碰到我军城堡时,若上一次更新的值为空位置,记录较大的摧毁数。
解题代码:
class Solution {public int captureForts(int[] forts) {int res=0;int lastEmpty=-1;int lastCommand=-1;for(int i=0;i<forts.length;i++){if(forts[i]==-1){if(lastCommand!=-1 && lastCommand>lastEmpty){res=Math.max(res,i-lastCommand-1);}lastEmpty=i;}else if(forts[i]==1){if(lastEmpty!=-1 && lastEmpty>lastCommand){res=Math.max(res,i-lastEmpty-1);}lastCommand=i;}}return res;}
}总结:
注意不能越过我军城堡去往空地。
无官方题解。
fort 城堡、堡垒
capture 俘获,采集,拍摄
相关文章:

题目:2511.最多可以摧毁的敌人城堡数量
题目来源: leetcode题目,网址:2511. 最多可以摧毁的敌人城堡数目 - 力扣(LeetCode) 解题思路: 顺序遍历数组,记录上一个我军城堡和没有城堡的位置。当碰到空位置时,若上一次更新的…...

22 | 书籍推荐数据分析
import numpy as np import pandas as pd import seaborn as sns import matplotlib.pyplot as plt from sklearn.cluster import KMeans from sklearn import neighbors from sklearn.model_selection import train_test_split from sklearn.preprocessing import...

vscode extension 怎么区分dev prod
开发模式注入环境变量 使用vsode 提供的api...

Java学习手册——第一篇Java简介
今后Java学习手册就来给大家梳理JavaSE的基础知识啦, 除了这个专栏我们还有其他专栏:前端、安全、后端等。 希望大家可以在这里一起讨论学习哟~ Java学习手册——第一篇Java简介 1. Java基础知识2. Java能干嘛3. Java基础环境搭建 1. Java基础知识 出生…...
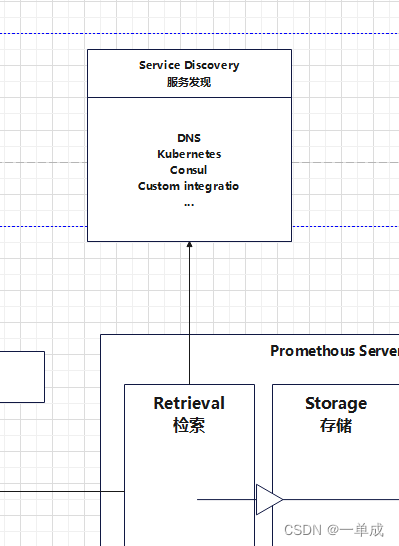
Prometheus流程图(自绘)-核心组件-流程详解
阿丹手绘流程图:图片可能有点小查看的时候放大看看哈! prometheus核心组件 prometheus server Prometheus Server是Prometheus组件中的核心部分,负责实现对监控数据的获取,存储以及查询。Prometheus Server可以通过静态配置管理…...

回归模型常见评估指标mae,mse,rmse
文章目录 MAE(平均绝对误差)计算公式sklearn实现numpy实现mse(均方误差)计算公式sklearn实现numpy实现rmse(均方根误差)计算公式sklearn实现MAE(平均绝对误差) 计算公式 MAE ( y ,...

服务器数据恢复-断电导致ext4文件系统文件丢失的数据恢复案例
服务器数据恢复环境: 一台服务器挂载一台存储设备,存储中划分一个Lun;服务器操作系统是Linux centos,EXT4文件系统。 服务器故障&分析: 意外断电导致服务器操作系统无法启动,系统在修复后可以正常启动&…...

链表(基础详解、实现、OJ笔试题)
文章目录 🧚什么是链表(链表概念及分类)链表分类单链表和双链表的区别 🚴♂️单链表、双向链表的实现单链表的实现双向链表的实现 🍉链表经典OJ笔试题反转单链表移除链表元素合并两个有序链表链表分割链表的中间结点…...
W5100S-EVB-PICO作为TCP Client 进行数据回环测试(五)
前言 上一章我们用W5100S-EVB-PICO开发板通过DNS解析www.baidu.com(百度域名)成功得到其IP地址,那么本章我们将用我们的开发板作为客户端去连接服务器,并做数据回环测试:收到服务器发送的数据,并回传给服务…...
大数据-玩转数据-Redis 安装与使用
一、说明 大多数企业都是基于Linux服务器来部署项目,而且Redis官方也没有提供Windows版本的安装包。因此课程中我们会基于Linux系统来安装Redis. 此处选择的Linux版本为CentOS 7. Redis的官方网站地址:http://download.redis.io/releases 二、下载 m…...

实时指标-1日留存率
2个DWD层 登录→kafka注册→kafka1个DWS 弄2条流,从kafka读取数据将昨日注册数据存到状态中,TTL为2天,存到map状态中,key为注册日期,value为set,存储注册的uid将登录流和注册流进行连接来一条登录数据&…...

【玩转23种Java设计模式】行为型模式篇:责任链模式
软件设计模式(Design pattern),又称设计模式,是一套被反复使用、多数人知晓的、经过分类编目的、代码设计经验的总结。使用设计模式是为了可重用代码、让代码更容易被他人理解、保证代码可靠性、程序的重用性。 汇总目录链接&…...

【C#】获取电脑CPU、内存、屏幕、磁盘等信息
通过WMI类来获取电脑各种信息,参考文章:WMI_04_常见的WMI类的属性_wmi scsilogicalunit_fantongl的博客-CSDN博客 自己整理了获取电脑CPU、内存、屏幕、磁盘等信息的代码 #region 系统信息/// <summary>/// 电脑信息/// </summary>public p…...

途乐证券-最准确的KDJ改良指标?
KDJ目标是技术剖析的一种重要目标之一,它是利用随机目标(%R)发展而来的,是一种反映商场超买和超卖状况的买卖目标。KDJ目标由快线(K线)、慢线(D线)和随机值(J线ÿ…...
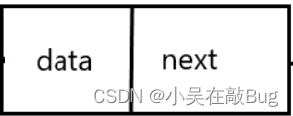
数据结构——线性表
文章目录 线性表的定义和基本操作顺序表线性表的链式表示 线性表的定义和基本操作 线性表是具有相同数据类型的(n≥0)个数据元素的有限序列,其中n为表长,当n0时线性表是一个空表。若用L命名线性表,则其中一般表示为:L(a1,a2,a3, …...
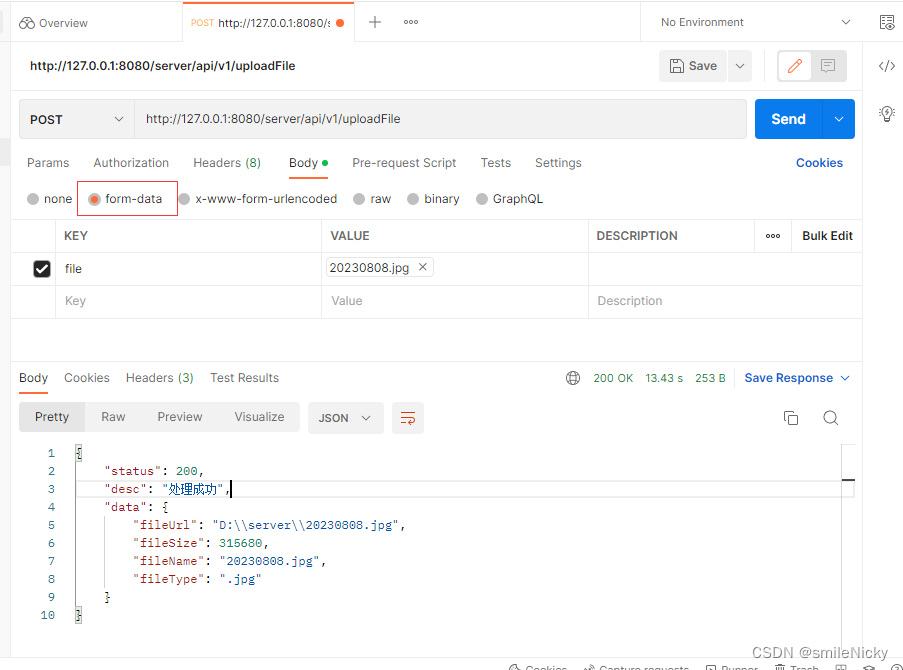
SpringBoot系列之基于Jersey实现文件上传API
前言 JAX-RS:JAX-RS是可以用可以用于实现RESTFul应用程序的JAVA API,给开发者提供了一系列的RESTFul注解Jersey:是基于JAX-RX API的实现框架,用于实现RESTful Web 服务的开源框架。 JAX-RX常用的注解: javax.ws.rs.Pa…...

【LangChain】Prompts之示例选择器
LangChain学习文档 【LangChain】向量存储(Vector stores)【LangChain】向量存储之FAISS【LangChain】Prompts之Prompt templates【LangChain】Prompts之自定义提示模板【LangChain】Prompts之示例选择器 概要 如果您有大量示例,您可能需要选择要包含在提示中的哪…...

Neo4j之CREATE基础
在 Neo4j 中,CREATE 语句用于创建节点、关系以及节点属性。 创建节点: CREATE (p:Person {name: John, age: 30});这个查询会创建一个具有 "Person" 标签的节点,节点属性包括 "name" 和 "age"。 创建带有关…...

Kali Hyper-V安装正常启动后 黑屏 只能进命令模式
问题: Hyper-V安装虚拟机Kali系统一切安装正常, 没有出现错误. 安装成功后重启,只能进入命令模式,tt1-tt6,进不去GUI桌面. 尝试: 一代二代虚拟硬盘都试过,同样问题,只能开进后进入命令模式,在命令模式下一切运行正常, 也修复过系统 GNOM等的,不管用. 以下为国外论坛给的建议,尝…...

【人工智能124种任务大集合】-集齐了自然语言处理(NLP),计算机视觉(CV),语音识别,多模态等任务
大家好,我是微学AI,今天给大家介绍一下人工智能124种任务大集合,任务集合主要包括4大类:自然语言处理(NLP)、计算机视觉(CV)、语音识别、多模态任务。 我这里整理了124种应用场景任…...

(十)学生端搭建
本次旨在将之前的已完成的部分功能进行拼装到学生端,同时完善学生端的构建。本次工作主要包括: 1.学生端整体界面布局 2.模拟考场与部分个人画像流程的串联 3.整体学生端逻辑 一、学生端 在主界面可以选择自己的用户角色 选择学生则进入学生登录界面…...

【入坑系列】TiDB 强制索引在不同库下不生效问题
文章目录 背景SQL 优化情况线上SQL运行情况分析怀疑1:执行计划绑定问题?尝试:SHOW WARNINGS 查看警告探索 TiDB 的 USE_INDEX 写法Hint 不生效问题排查解决参考背景 项目中使用 TiDB 数据库,并对 SQL 进行优化了,添加了强制索引。 UAT 环境已经生效,但 PROD 环境强制索…...

如何在看板中体现优先级变化
在看板中有效体现优先级变化的关键措施包括:采用颜色或标签标识优先级、设置任务排序规则、使用独立的优先级列或泳道、结合自动化规则同步优先级变化、建立定期的优先级审查流程。其中,设置任务排序规则尤其重要,因为它让看板视觉上直观地体…...

解锁数据库简洁之道:FastAPI与SQLModel实战指南
在构建现代Web应用程序时,与数据库的交互无疑是核心环节。虽然传统的数据库操作方式(如直接编写SQL语句与psycopg2交互)赋予了我们精细的控制权,但在面对日益复杂的业务逻辑和快速迭代的需求时,这种方式的开发效率和可…...

基础测试工具使用经验
背景 vtune,perf, nsight system等基础测试工具,都是用过的,但是没有记录,都逐渐忘了。所以写这篇博客总结记录一下,只要以后发现新的用法,就记得来编辑补充一下 perf 比较基础的用法: 先改这…...

Spring Boot面试题精选汇总
🤟致敬读者 🟩感谢阅读🟦笑口常开🟪生日快乐⬛早点睡觉 📘博主相关 🟧博主信息🟨博客首页🟫专栏推荐🟥活动信息 文章目录 Spring Boot面试题精选汇总⚙️ **一、核心概…...

laravel8+vue3.0+element-plus搭建方法
创建 laravel8 项目 composer create-project --prefer-dist laravel/laravel laravel8 8.* 安装 laravel/ui composer require laravel/ui 修改 package.json 文件 "devDependencies": {"vue/compiler-sfc": "^3.0.7","axios": …...

Unsafe Fileupload篇补充-木马的详细教程与木马分享(中国蚁剑方式)
在之前的皮卡丘靶场第九期Unsafe Fileupload篇中我们学习了木马的原理并且学了一个简单的木马文件 本期内容是为了更好的为大家解释木马(服务器方面的)的原理,连接,以及各种木马及连接工具的分享 文件木马:https://w…...

2025季度云服务器排行榜
在全球云服务器市场,各厂商的排名和地位并非一成不变,而是由其独特的优势、战略布局和市场适应性共同决定的。以下是根据2025年市场趋势,对主要云服务器厂商在排行榜中占据重要位置的原因和优势进行深度分析: 一、全球“三巨头”…...

算法岗面试经验分享-大模型篇
文章目录 A 基础语言模型A.1 TransformerA.2 Bert B 大语言模型结构B.1 GPTB.2 LLamaB.3 ChatGLMB.4 Qwen C 大语言模型微调C.1 Fine-tuningC.2 Adapter-tuningC.3 Prefix-tuningC.4 P-tuningC.5 LoRA A 基础语言模型 A.1 Transformer (1)资源 论文&a…...
