个人对哈希数据结构学习总结 -- 理论篇
个人对哈希数据结构学习总结 -- 理论篇
- 引言
- 哈希表设计思考
- 哈希冲突
- Hash Functions
- 冲突解决
- 开放地址法(Open Addressing)
- 分离链表法(Separate Chaining)
- Two-way Chaining
- Dynamic Hash Tables
- chained Hashing
- extendible hashing
- linear hashing
- 说明
- spiral storage
- 使用场景
- 小结
引言
哈希表这个数据结构相信各位都不陌生,无论是高级语言,还是各大数据库底层实现都不离开它,所以本文我想来聊聊我个人对哈希表的一些看法,同时也是对哈希表这个知识点做一次系统性的梳理和总结。
本文主要会分为两大部分:
- 哈希表设计思考(偏理论)
- 最佳实践(结合Java,Go,redis等热门技术来谈谈其中使用到的哈希设计原则)
哈希表设计思考
对于哈希表这个数据结构而言,有这样四个维度的指标是我们需要考虑的:
- 所有数据集合 S
- 哈希表存储的数据集合 U
- 所有哈希桶的下标集合 R
- 映射函数 h
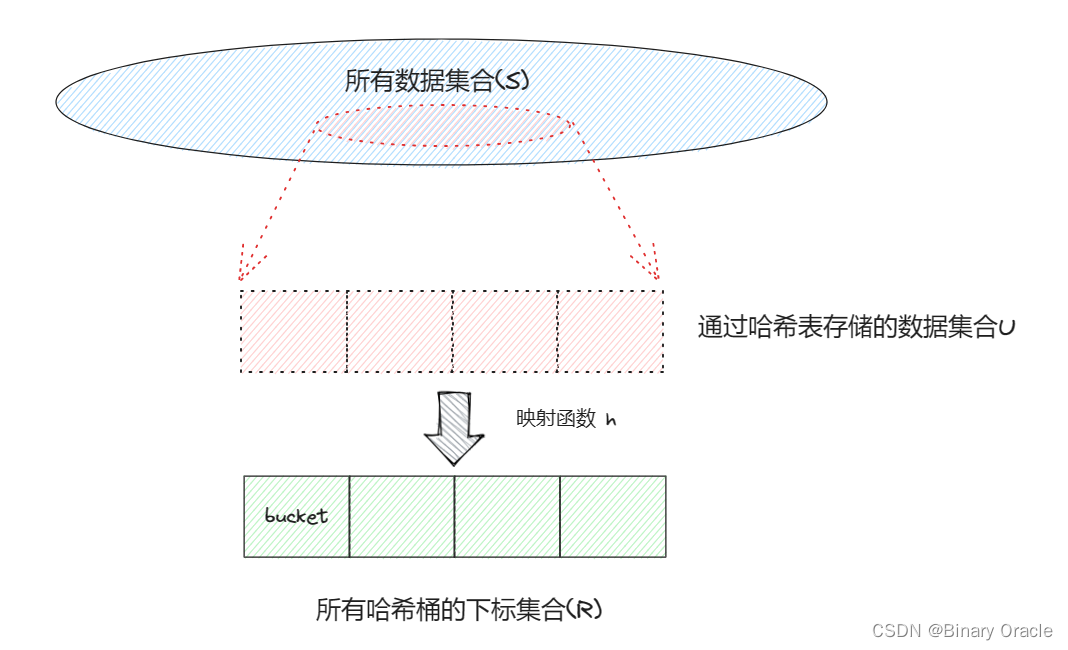
S的大小一般远大于R,但是哈希表存储的数据集合 U 与 R 大小相差不会太大;如果存在 x!=y && h(x) == h(y) ,则称x与y冲突。
如果h可以将U单射到R上,那么我们称这种情况为完美哈希(perfect hashing) , 并且如果此时U的大小与R的大小相等,则称此种情况为最小完美哈希(minimal perfect hashing)。
如果U的大小是固定的并且预先可知,那么称这种情况为静态哈希表,否则称之为动态哈希表。
哈希冲突
解决哈希冲突有两个着眼点:
- 在冲突没发生前尽量避免冲突,在冲突发生后解决冲突
Hash Functions
要避免冲突,我们需要从哈希函数h这个维度下手:
- 对于静态哈希表,我们总是可以找到一个h来达成最小完美哈希
- 对于动态哈希表,由于集合U是不可控的,所以我们的思路是尽可能减少冲突发生,也就是选择一个尽可能少冲突的哈希函数h
关于如何设计一个完美的哈希函数并不是本文重点,但是比较出名的哈希函数有以下这些,大家可以自行查阅资料了解各自适用场景:
- MurmurHash (2008)
- Google CityHash (2011)
- Google FarmHash (2014)
- CLHash (2016)
冲突解决
动态哈希表很难达成完美哈希的情况,因此我们必须考虑如何解决发生的哈希冲突,常见的冲突解决策略有:
- 开放地址法(Open Addressing)
- 分离链表法(Separate Chaining)
- Two-way Chaining
开放地址法(Open Addressing)
开放地址法(Open Addressing)下面又细分了好几种策略:
- 线性探测法(Linear Probing):发生哈希冲突时,将会在哈希表中线性地往后查找,直到找到一个空槽来插入元素或执行查找操作。
- 这种方法可能导致聚集(clustering)现象,即冲突的元素会聚集在一起,影响性能。
- 二次探测法(Quadratic Probing): 发生冲突时,会使用二次函数来计算下一个探测位置,以尝试寻找下一个空槽或者目标元素。
- 这种方法相对于线性探测法来说,能够更均匀地分散元素,但仍然可能会出现二次探测路径相交的情况。
- 双重散列(Double Hashing):双重散列使用两个哈希函数,当发生冲突时,首先使用第一个哈希函数得到一个偏移量,然后在第二个哈希函数的值处查找下一个位置。
- 这个方法可以有效地减少聚集问题,但需要选择合适的哈希函数和冲突解决策略。
其中 Linear probing 由于对缓存友好,性能最高,比较常用。Linear probing 可能带来冲突聚集的情况,为了避免这一现象,有时也会使用 Quadratic probing 策略。使用 Quadratic probing 也会遇到一些恶意操作或者特定的输入数据,从而导致性能下降或其他问题,因此有时也会使用 Double hashing 配合 Universal hashing 获得更好的效果。
1.“线性探测对缓存友好” 指的是线性探测法在某些情况下能够更好地利用计算机的缓存机制,从而在内存访问方面表现较好。这主要是因为线性探测法在哈希冲突时,会沿着一个连续的内存地址序列进行探测,这有助于提高数据的局部性,从而更好地适应现代计算机的缓存体系结构。
2.通用哈希(Universal hashing)的主要思想是,从一组可能的哈希函数中随机选择一个函数来哈希每个键,这样可以使得不同的键在不同的哈希函数下分布,减少冲突的概率。
Robin Hood Hashing:
- Linear Probe Hashing 的变种,为了防止 Linear Probe Hashing 出现连续区域导致频繁的 probe 操作。基本思路是 “劫富济贫”,即每次比较的时候,同时需要比较每个 key 距离其原本位置的距离(越近越富余,越远越贫穷),如果遇到一个已经被占用的 slot,如果它比自己富余,则可以直接替代它的位置,然后把它顺延到新的位置。
- Robin Hood Hashing 也是为了解决线性探测法冲突聚集的问题
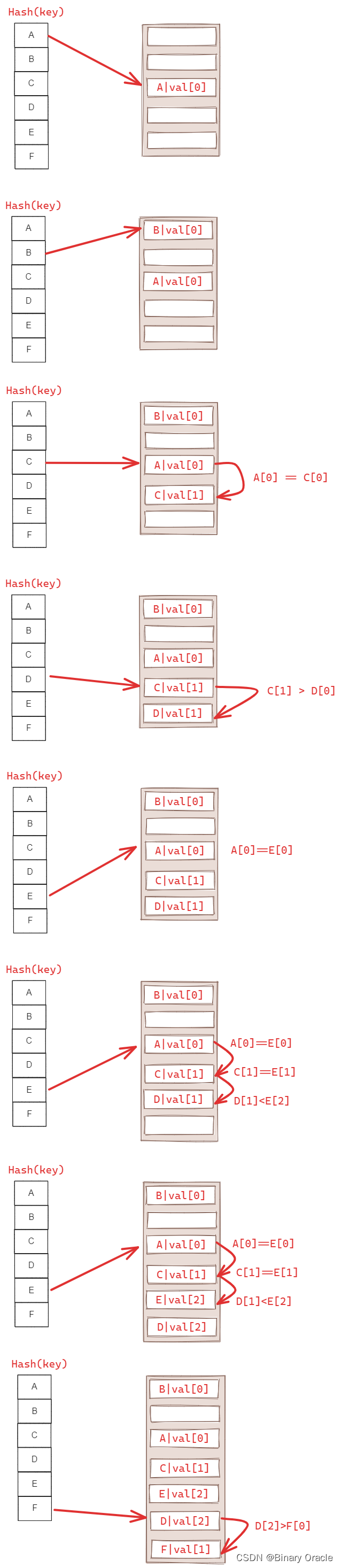
这样做的好处是什么呢?最大的好处就是各个键值对离自己的理想位置的距离变得“均衡”了,或许对查询的平均时间复杂度有一定的优化,但是一定复杂化了插入操作的时间复杂度。
实际上,经过实验发现,这种方法的效率不如线性探测法,不过这种方法的思想还是很有价值的。
分离链表法(Separate Chaining)
开放地址法(Open Addressing) 在装载因子较高时性能会急剧下降,为了应对这一情况,也常使用 Separate Chaining 策略。Separate Chaining 一般使用链表,有时也会使用查找树结构。
Two-way Chaining
Two-way Chaining 就像是 Double hashing,区别在于 Double hashing 使用一个哈希表,而 Two-way Chaining 使用两个哈希表 T1 和 T2。在插入时,T[h1(x)] 和 T[h2(x)] 中哪个装载的元素更少,就插入到哪儿。查找时需要访问两个哈希表。
还有一种和Two-way Chanining思想类似的算法Cuckoo Hashing (布谷鸟哈希) ,要理解该算法,我们首先需要理解布谷鸟的行为,这也是算法的核心:
- 布谷鸟妈妈从不筑巢,它将自己的鸟蛋生在其他鸟类的巢穴里,要别的鸟给它孵蛋
- 新出生的布谷鸟会本能地将巢穴里的其他蛋踢开(kick out ),推出鸟巢,以确保自己在鸟巢里可以独享宠爱
布谷鸟哈希有几种变种,下面介绍一个哈希桶和两个哈希函数的版本:
-
Insert
- 若值x已存在哈希表中,则直接返回
- 若insert后哈希表空间会不够,则先进行扩容,再rehash,再继续3、4、5
- 用哈希函数h1(x)计算出下标i1,当bucket[i1]为空时,说明鸟巢可用,插入x
- 若bucket[i1]非空,用新值x将bucket[i1]上的老值x’踢开(kick out),对应小布谷鸟将老蛋踢出巢穴,老蛋当然也不能坐以待毙,继续kick out别的蛋,老值x’的下一个位置用哈希函数h2(x)寻找
- 重复2,直到达到最大循环次数MaxLoop(插入失败);或者所有被踢开的值都找到新位置(插入完成)
-
lookup
- 查找逻辑非常简单,去可能的两个巢穴里寻找,即去下标h1(x)和h2(x)寻找,若没有匹配上,则不存在
(从这里可以发现查找是非常快的,且时间复杂度稳定是O(1))
- 查找逻辑非常简单,去可能的两个巢穴里寻找,即去下标h1(x)和h2(x)寻找,若没有匹配上,则不存在
下图展示的是两个哈希函数,两个哈希桶的版本:
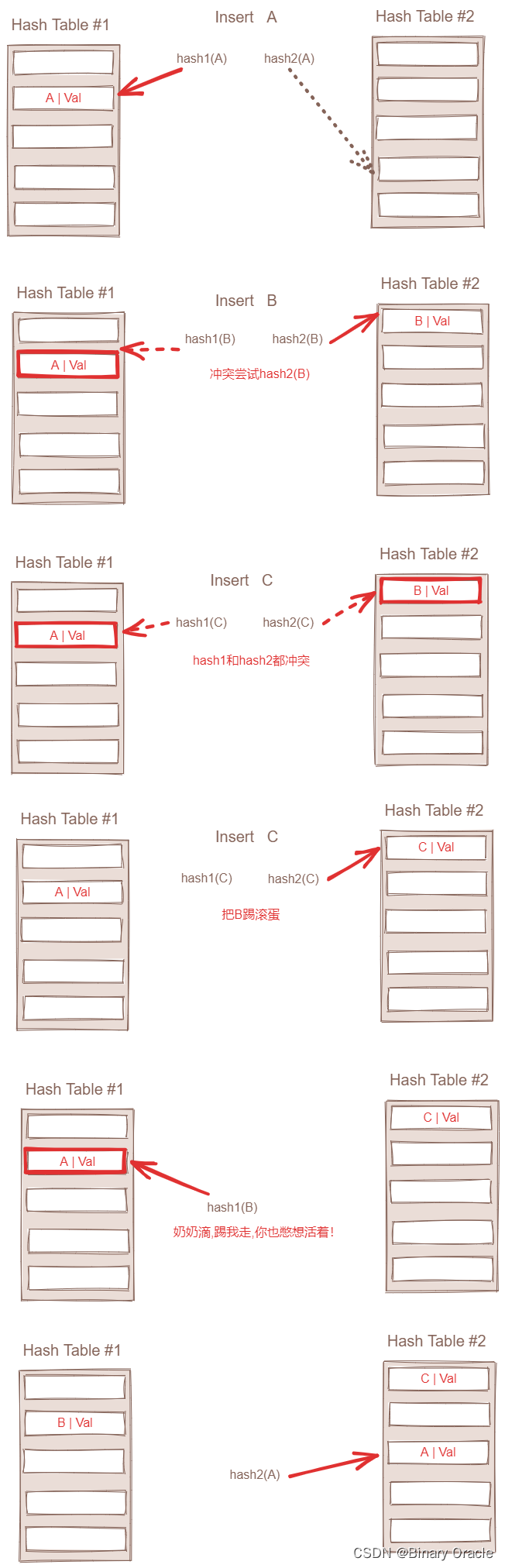
为了防止我们不会陷入一个无限循环中,一旦我们发现了一个死循环或者达到最大循环次数,我们就需要对现有的hash table进行扩容:
- 如果使用两个hash function,那么我们大概只需要当hash table达到50%容量左右时,才需要进行扩容重建
- 如果使用三个hash function,那么我们大概需要当hash table达到90%容量的左右时,才需要进行扩容重建
Dynamic Hash Tables
随着哈希表的装载因子上升,哈希冲突的概率会不断上升,直到装载因子超过 1 时,必然发生哈希冲突。对于动态哈希表,由于U 的大小不能预先得知,所以必然需要动态调整哈希表的大小。常见的策略:
- 当装载因子超过某一阈值后,线性扩展哈希表的大小为原来的若干倍
- 当装载因子低于某一阈值时,线性收缩哈希表的大小为原来的若干分之一
使用两个阈值的原因是为了避免抖动。
由于R发生变化,对应的哈希函数也必须发生变化,同时分配一个块更大的内存,将原哈希表中所有元素rehash到新的哈希表中,这种策略称为Copy All策略,该策略的坏处就是会产生较长时间的停顿,因此下面来介绍几种改进的策略:
- Chained Hashing
- extendible hashing
- linear hashing
- spiral storage
哈希表不能够均匀地增长,其根本原因在于 rehash,只要能够不 rehash 但是调整 R,就可以解决这一问题。
chained Hashing
Chained Hashing 是 Dynamic Hash Tables 的 HelloWorld 实现,每个 key 对应一个链表,每个节点是一个 bucket,装满了就再往后挂一个 bucket。需要写操作时,需要请求 latch:
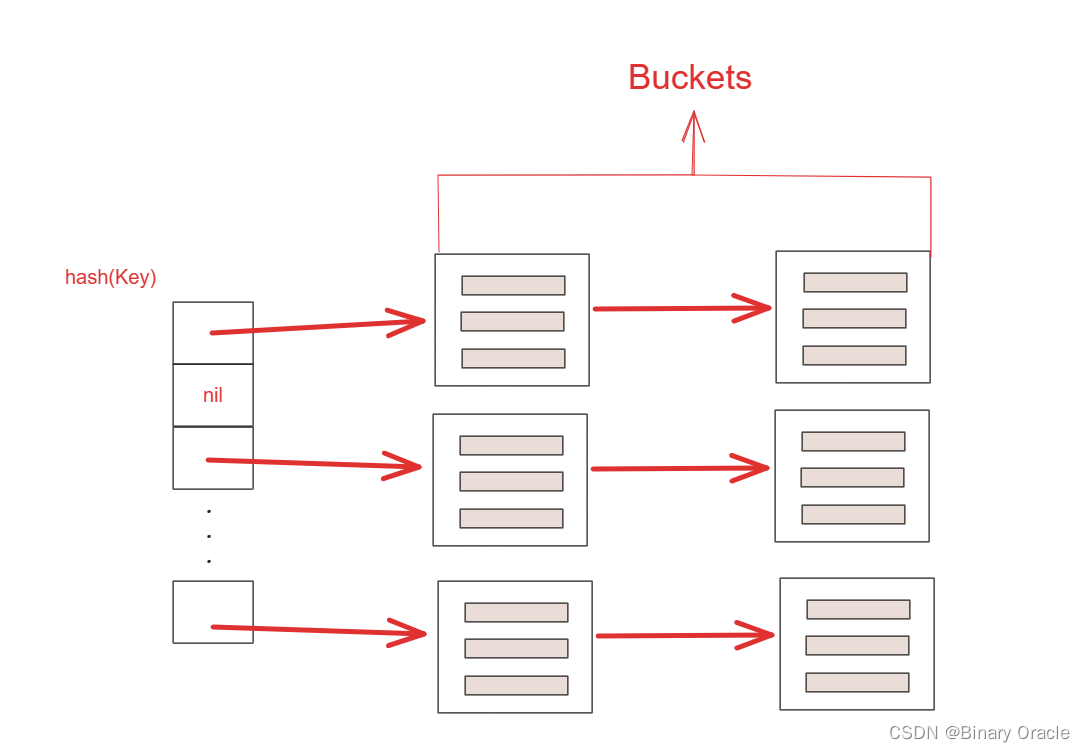
- 在查找元素时,根据元素的哈希键计算出对应的槽位,并遍历该槽位的链表桶,搜索具有相同哈希键的元素
- 对于插入和删除操作,也可以看作是查找操作的一般化。在插入元素时,需要进行查找并确定插入位置;在删除元素时,也需要查找并删除相应元素
这么做的好处就是简单,坏处就是最坏的情况下 Hash Table 可能降级成链表,使得操作的时间复杂度降格为 O(n)。
当然,如果桶中只有一个元素,那么可以将其视为链表,可以在链表长度到达指定阈值后,变成二叉查找树,提升查询效率。并且当负载因子达到指定阈值后,可以对哈希表进行扩容,此时如果不考虑性能,可以采用copy all策略,如果考虑性能,可以考虑渐进式扩容策略。
extendible hashing
在Chained Hashing中,一种可行的方法是在链表变得过长时,将桶(bucket)进行分割,而不是让链表无限增长。这种方法可以避免链表过长导致的性能问题,并且需要进行分割时,只需要对特定的桶进行重新分配。
可扩展哈希方式包含一个slot数组和一系列的buckets,每个slot中保存对应bucket的指针。对于slot数组有一个全局bit位,记录在这个哈希表中需要多少位才能找到对应bucket,对于每一个bucket,有一个本地bit位,记录找到本地的bucket需要多少位。
extendible hash像一种结合hash与redix(前缀树)的技术的哈希方法
Extendible Hashing 的基本思路是一边扩容,一边 rehash,如下图所示:
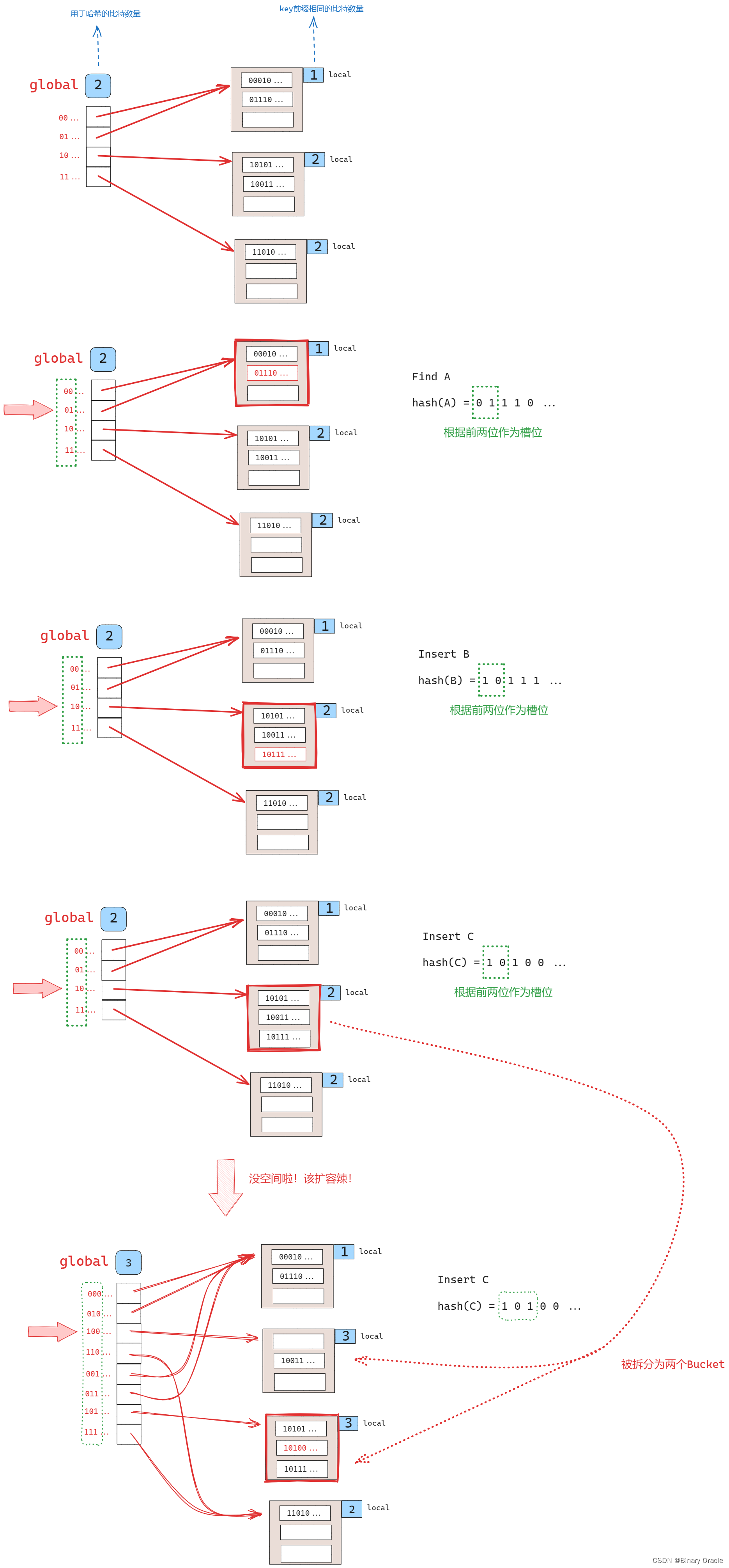
可拓展哈希允许插入哈希值相同的记录。所以当插入4条哈希值一样的记录,一个桶就一定放不下(假设桶的容纳上限是3条)。这种情况被叫做overflow,而解决方法是用指针指向overflow bucket,也就是人为增加桶。这种方式看上去不美,也暴露了可拓展哈希的局限性,但一个方法在实际应用中确实无法确保永远的统一性,总是会需要“补丁”。实际应用中,可拓展哈希也不是最普遍的方法,更多则是B-Tree。
linear hashing
本部分参考文章
线性哈希是可扩展哈希的改进,可扩展哈希有一个小的性能瓶颈,在bucket分裂且需要扩展slot array时,需要对整个slot array加锁直到bucket分裂完成。为了解决这个问题,提出了线性哈希方式。哈希表维护一个指针,指向下一个准备分裂的bucket,并且线性哈希采用多个哈希函数来寻找正确的bucket。
线性哈希的数学原理:
- 假定key = 5 、 9 、13
此时所有 key % 4 = 1
- 现在我们对8求余
5 % 8 = 59 % 8=113 % 8 = 5
由上面的规律可以得出
- (任意key) % n = M
- (任意key) %2n = M或 (任意key) %2n = M + n
线性哈希的具体实现如所示:
- 我们假设初始化的哈希表如下:
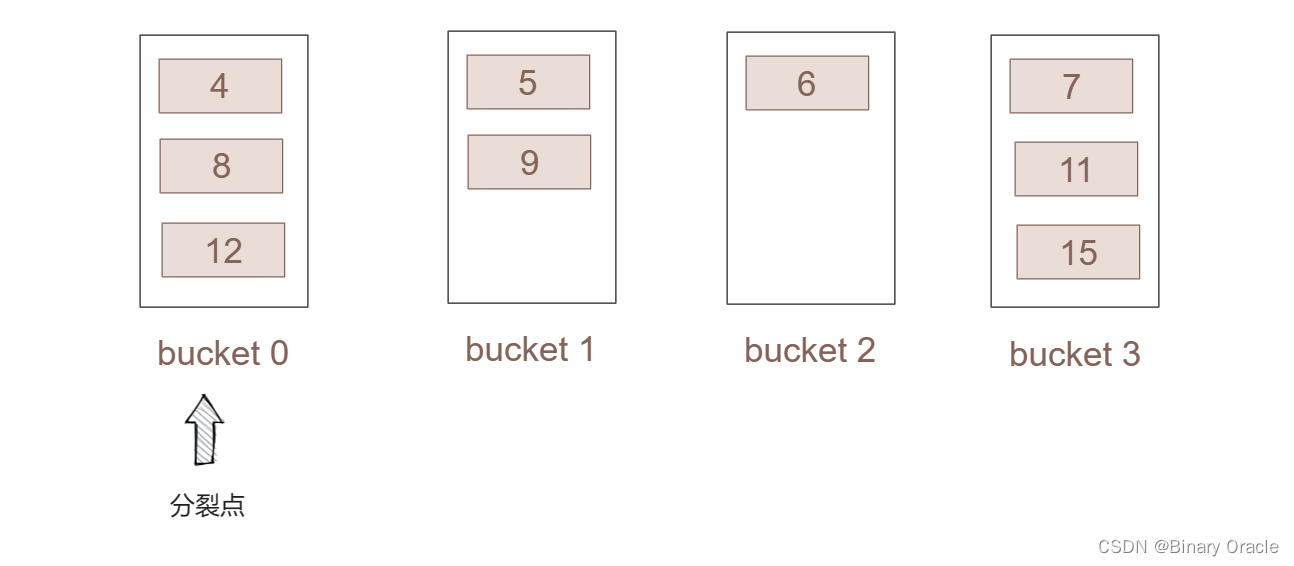
为了方便叙述,我们作出以下假定:
- 为了使哈希表能进行动态的分裂,我们从桶0开始设定一个分裂点。
- 一个桶的容量为listSize = 3,当桶的容量超出后就从分裂点开始进行分裂。
- hash函数为 h0 = key %4 h1 = key % 8,h1会在分裂时使用。
- 整个表初始化包含了4个桶,桶号为0-3,并已提前插入了部分的数据。
分裂过程如下:
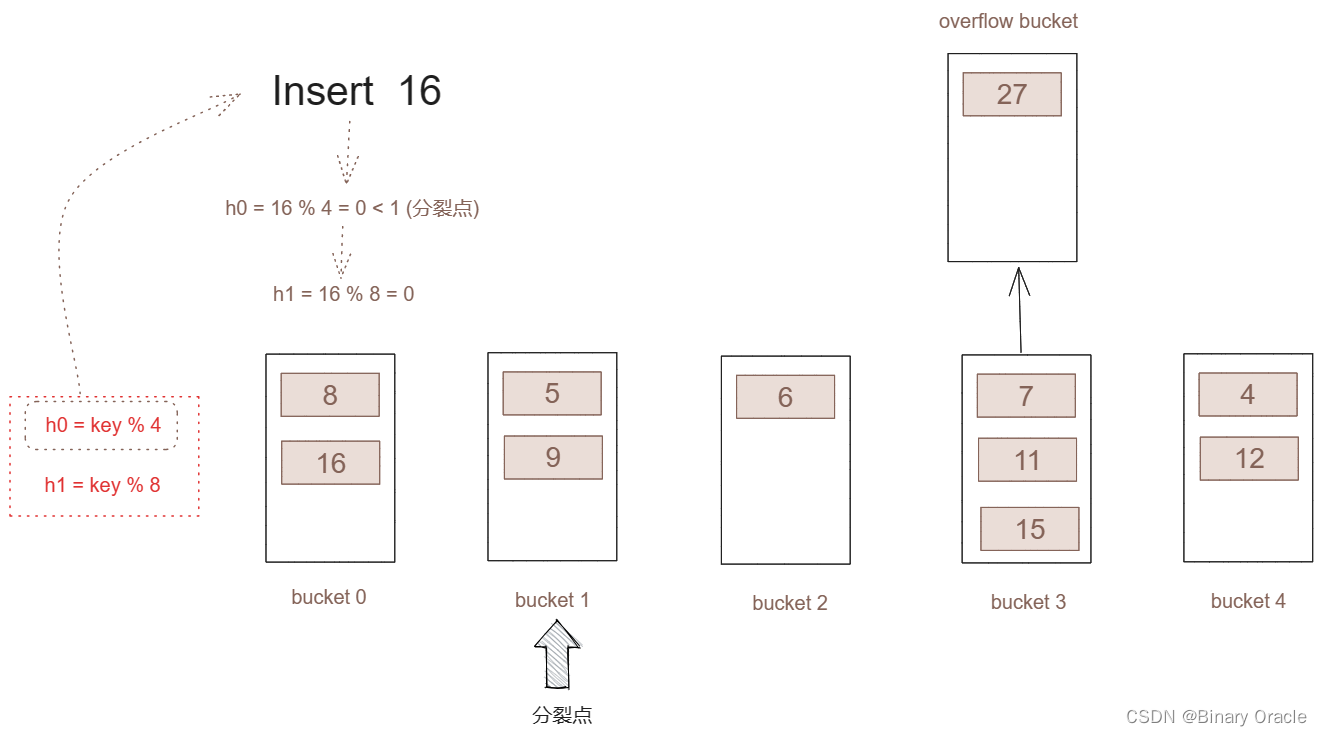
现在插入key = 27
-
进行哈希运算,h0 = 27 % 4 = 3
-
将key = 27插入桶3,但发现桶3已经达到了桶的容量,所以触发哈希分裂
-
由于现在分裂点处于0桶,所以我们对0桶进行分割。这里需要注意虽然这里是3桶满了,但我们并不会直接从3桶进行分割,而是从分割点进行分割。这里为什么这么做,在下面会进一步介绍。
-
对分割点所指向的桶(桶0)所包含的key采用新的hash函数(h1)进行分割。
对所有key进行新哈希函数运算后,将产生如下的哈希表:
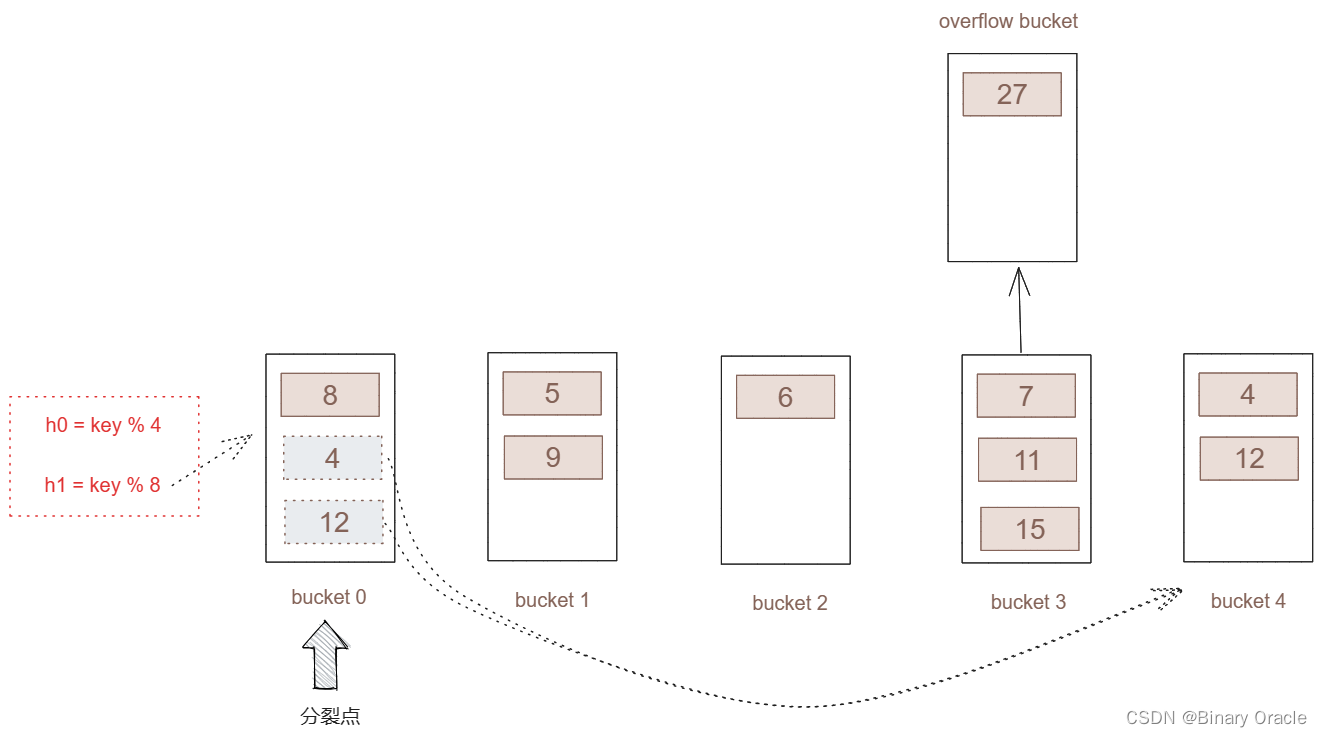
- 虽然进行了分裂,但桶3并不是分裂点,所以桶3会将多出的key,放于溢出桶.,一直等到桶3进行分裂。
- 进行分裂后,将分裂点向后移动一位。
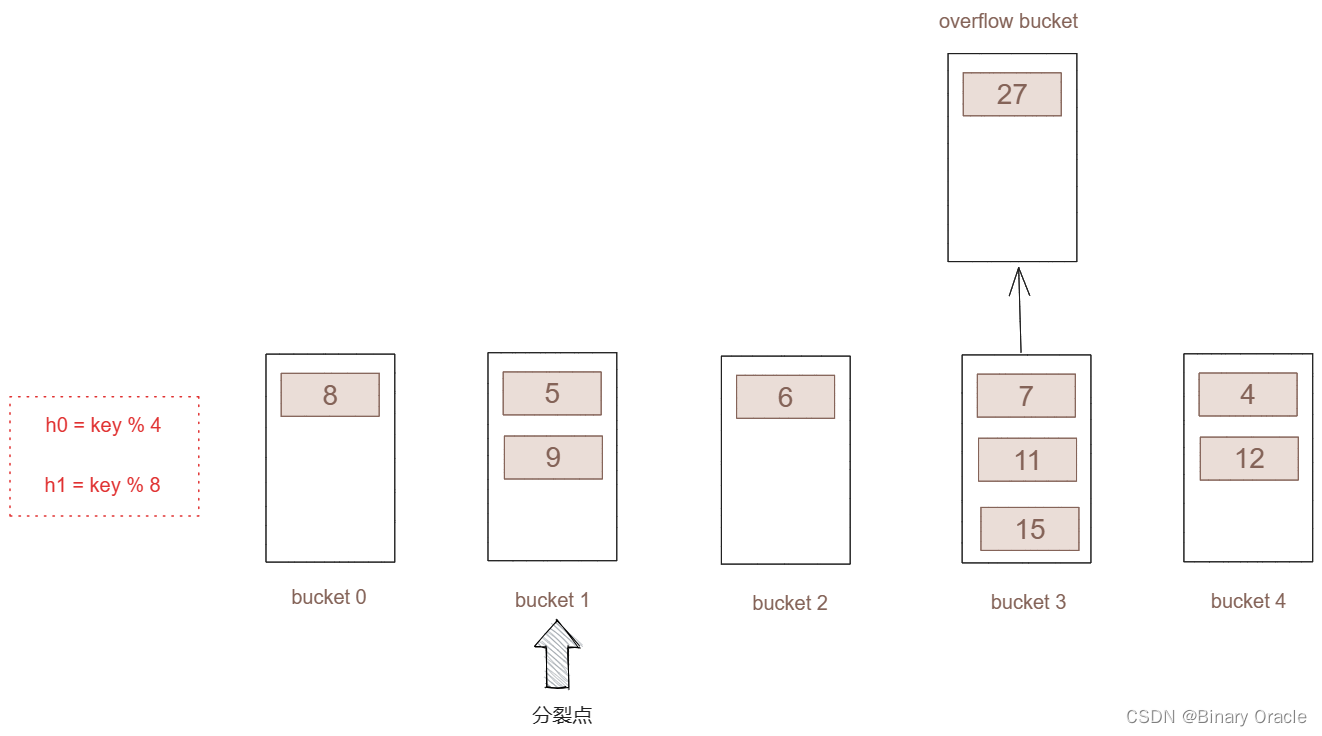
- 一次完整的分裂结束
key的读取:
- 采用h0对key进行计算。
- 如果算出的桶号小于了分裂点,表示桶已经进行的分裂,我们采用h1进行hash运算,算出key所对应的真正的桶号。再从真正的桶里取出value
- 如果算出的桶号大于了分裂点,那么表示此桶还没进行分裂,直接从当前桶进行读取value。
说明
-
如果下一次key插入0、1、2、4桶,是不会触发分裂(没有超出桶的容量), 如果是插入桶3,用户在实现时可以自己设定,可以一旦插入就触发,也可以等溢出桶达到listSize再触发新的分裂。
-
现在0桶被分裂了,新数据的插入怎么才能保证没分裂的桶能正常工作,已经分裂的桶能将哪部分插入到新分裂的桶呢?
-
只要分裂点小于桶的总数,我们依然采用h0函数进行哈希计算。
-
如果哈希结果小于分裂号,那么表示这个key所插入的桶已经进行了分割,那么我就采用h1再次进行哈希,而h1的哈希结果就这个key所该插入的桶号。
-
如果哈希结果大于分裂号,那么表示这个key所插入的桶还没有进行分裂。直接插入。
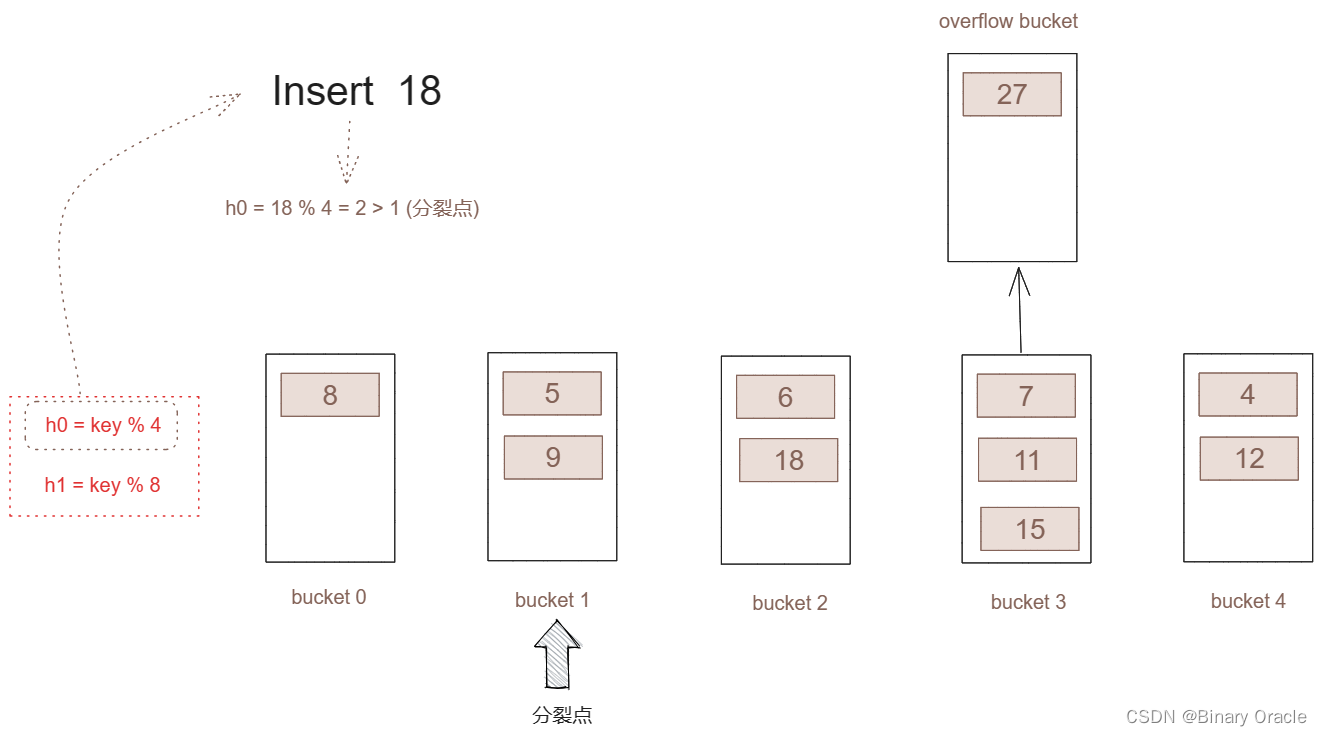
-
这也是为什么虽然是桶3的容量不足,但分裂的桶是分裂点所指向的桶。如果直接在桶3进行分裂,那么当新的key插入的时候就不能正常的判断哪些桶已经进行了分裂。
-
-
如果使用分割点,就具备了无限扩展的能力。当分割点移动到最后一个桶(桶3)。再出现分裂。那么分割点就会回到桶0,到这个时候,h0作废,h1替代h0, h2(key % 12)替代h1。那么又可以开始动态分割。那个整个初始化状态就发生了变化。就好像没有发生过分裂。那么上面的规则就可以循环使用。
-
线性哈希的论文中是按上面的规则来进行分裂的。其实我们可以安装自己的实际情况来进行改动。
假如我们现在希望去掉分割点,一旦哪个桶满了,马上对这个桶进行分割。
可以考虑了以下方案:
-
为所有桶增加一个标志位。初始化的时候对所有桶的标志位清空。
-
一旦某个桶满了,直接对这个桶进行分割,然后将设置标志位。当新的数据插入的时候,经过哈希计算(h0)发现这个桶已经分裂了,那么就采用新的哈希函数(h1)来计算分裂之后的桶号。在读取数据的时候处理类似。
采用此种方案实现的LinerHash简易代码如下所示:
/*** lineHash简单实现模型*/
public class LineHash {/*** 单桶最多容纳元素个数*/public final int bucketMaxSize;/*** 分裂点索引*/public int overPoint = 0;/*** 每一轮的哈希桶数组初始大小*/private int initSize;/*** 哈希桶数组*/public Bucket[] buckets;public LineHash(int bucketMaxSize) {this.bucketMaxSize = bucketMaxSize;// 初始桶数组大小为4buckets = new Bucket[4];initSize = 4;}public String get(int key) {int index = calculateIndex(key);return buckets[index].get(key);}public void put(int key, String val) {int index = calculateIndex(key);Bucket bucket = buckets[index];// 判断当前桶是否满了if (bucket.size() < bucketMaxSize) {bucket.put(key, val);} else {//满了就进行分裂bucket.put(key, val);splitHash();}}private int calculateIndex(int key) {//根据分裂轮数调用不同的哈希函数int index = hashFun(key, 1);//当前桶产生了分裂if (index < overPoint) {//采用新的哈希函数进行计算index = hashFun(key, 2);}lazyInitIfNeed(index);return index;}private void lazyInitIfNeed(int index) {if (buckets[index] == null) {buckets[index] = new Bucket(bucketMaxSize);}}public int hashFun(int key, int round) {return key % (initSize * round);}public void splitHash() {// 待分裂的旧桶Bucket oldBucket = buckets[overPoint];//分裂产生的新桶Bucket newBucket = new Bucket(bucketMaxSize);// 对旧桶中的元素进行rehashSet<Integer> keySet = oldBucket.keySet();List<Integer> removeKeyList=new ArrayList<>(oldBucket.size()/2);keySet.forEach(key -> {int index = hashFun(key, 2);// 说明当前key需要被rehash到新桶中if (index >= buckets.length) {newBucket.put(key, oldBucket.get(key));removeKeyList.add(key);}});removeKeyList.forEach(oldBucket::remove);// 将新桶添加进哈希桶数组中addBucket(newBucket);// 分裂点前移overPoint++;// 分裂点移动了一轮就更换新的哈希函数if (overPoint >= initSize) {initSize = initSize * 2;overPoint = 0;}}private void addBucket(Bucket newBucket) {Bucket[] temp = new Bucket[buckets.length + 1];System.arraycopy(buckets, 0, temp, 0, buckets.length);temp[buckets.length] = newBucket;buckets = temp;}/*** 桶*/private static class Bucket {private final Map<Integer, String> map;private Bucket(int bucketMaxSize) {this.map = new HashMap<>(bucketMaxSize);}public void put(Integer key, String val) {map.put(key, val);}public String get(Integer key) {return map.get(key);}public int size() {return map.size();}public Set<Integer> keySet() {return map.keySet();}public void remove(Integer key) {map.remove(key);}}
}
这段代码逻辑不完全正确,本人目前能力所限,对liner hash理解还不够透彻,如果有大佬有补充,可以在评论区留言。
关于Linear Hashing的更多内容,大家可以阅读论文学习:
- Linear Hashing Paper
spiral storage
Spiral Storage 总是将负载更多的放在哈希表靠前的位置上,而非均匀地将负载分配到整个哈希表中。这样尽管是像 Linear Hashing 一样,总是从哈希表的头部开始进行 bucket 的分裂,也不会有不及时处理非常满的 bucket 的问题。
Spiral Storage 的思路是这样的。哈希表的负载从前向后逐渐降低;扩展大小时,需要将表头的 bucket 中的元素分配到多个新 bucket 中并添加到哈希表的末尾,并且依然保持负载从前向后逐渐下降的性质。假设每去掉表头的一个 bucket 就添加 d 个新 bucket,称 d 为哈希表的增长因子。考虑到哈希表是非线性增加大小的,应该采用一个非线性增长的哈希函数族,将 U 映射到 R。易发现指数函数满足这样的性质。
spiral storage本节讲解的比较模糊,具体可以参考Google的开源实现:
- https://github.com/sparsehash/sparsehash
使用场景
单机场景:
- 对于静态哈希表而言,如果预先知道哈希表需要存储的数据集合U,那么我们要力求实现Minimal Perfect Hashing。
- 对于动态哈希表而言,如果可以预先知道部分数据的分布,那么可以针对性的设计哈希函数,尽可能达到Perfect Hashing。
- 如果没有关于数据的额外信息,我们可以在保证负载因子较低的情况下,尽量选择线性探测法(Linear Probing)来较好的利用CPU缓存。
- 在不能保证负载因子的情况下,如果需要考虑最坏情况的话,应该考虑使用分离链表法(Separate Chaining)配合平衡树搜索策略。
- 如果希望获得比较高的装载因子,同时又不希望性能下降太严重,并且可以接受一定的长尾的话,可以考虑布谷鸟哈希策略(Cuckoo Hashing)。
- 哈希表的动态大小调整一般选择Copy All策略,一方面实现简单,另一方面对哈希函数限制最小。
分布式场景:
- 分布式场景下,更多的问题在于如何快速将请求匹配到实际存储数据的节点,该场景下基本被一致性哈希所统治。
- 对于局域网(LAN)环境下的快速查找场景,如果期望常数级别的时间复杂度,最简单的方式就是缓存所有节点的映射信息。
因为哈希表一般需要保持比较低的负载因子,所以在哈希表较大的时元素会非常稀疏,如果需要支持SCAN操作的话,需要考虑在非空bucket之间建立联系。
小结
本篇作为笔者个人对哈希数据结构的学习总结的理论篇,主要和大家探讨了一下哈希数据结构的相关理论性基础知识,由于笔者个人能力有限,所以其中很多知识点笔者个人也仍然处在探索之路上,无法使用简单直白的语言表达出来,望各位见谅!
本文讲述内容其中可能含有大量理解偏差,如有大佬发现,可以在评论区指出,或者给出个人观点!
下一篇中,我将结合Java,Go,redis等热门技术来谈谈其中使用到的哈希设计原则。
相关文章:

个人对哈希数据结构学习总结 -- 理论篇
个人对哈希数据结构学习总结 -- 理论篇 引言哈希表设计思考哈希冲突Hash Functions冲突解决开放地址法(Open Addressing)分离链表法(Separate Chaining)Two-way Chaining Dynamic Hash Tableschained Hashingextendible hashinglinear hashing说明 spiral storage 使用场景小结…...
在CMamke生成的VS项目中插入程序
在主文件夹的CMakeLists.tex中加入SET(COMPILE_WITH_LSVM OFF CACHE BOOL "Compile with LSVM") 再添加IF(COMPILE_WITH_LSVM) MESSAGE("Compiling with: LSVM") ADD_DEFINITIONS(-DCOMPILE_WITH_LSVM) ADD_SUBDIRECTORY(LSVM) LIST(APPEND SRC LSVM_wrap…...

198、仿真-基于51单片机函数波形发生器调幅度频率波形Proteus仿真(程序+Proteus仿真+原理图+流程图+元器件清单+配套资料等)
毕设帮助、开题指导、技术解答(有偿)见文未 目录 一、硬件设计 二、设计功能 三、Proteus仿真图 四、原理图 五、程序源码 资料包括: 需要完整的资料可以点击下面的名片加下我,找我要资源压缩包的百度网盘下载地址及提取码。 方案选择 单片机的选…...

Django 初级指南:创建你的第一个 Django 项目
Django 是一个强大的 Python Web 框架,它采用了“模型-视图-控制器”(MVC)的设计模式,能够帮助开发者快速、简洁地创建高质量的 Web 应用。这篇文章将引导你创建你的第一个 Django 项目。 一、安装 Django 首先,你需…...

【MySQL】使用C++连接数据库
目录 前置工作代码常用函数接口整体示例: 前置工作 创建数据库并选中 mysql> create database conn; Query OK, 1 row affected (0.01 sec)mysql> show databases; -------------------- | Database | -------------------- | information_schema…...
php代码审计,php漏洞详解
文章目录 1、输入验证和输出显示2、命令注入(Command Injection)3、eval 注入(Eval Injection)4、跨网站脚本攻击(Cross Site Scripting, XSS)5、SQL 注入攻击(SQL injection)6、跨网站请求伪造攻击(Cross Site Request Forgeries, CSRF)7、Session 会话劫持(Session Hijacking…...
uniapp 将标题背景更换背景图片 完美解决(附加源码+实现效果图)
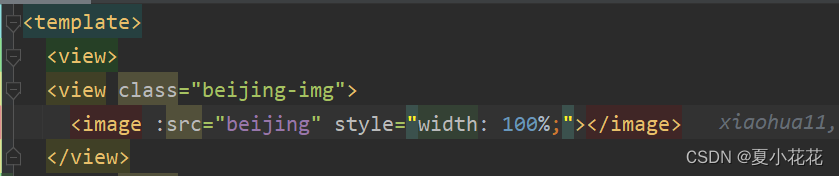
问题描述 今天拿到小程序的设计效果图后,标题部分背景需要加背景图片,以往我做的都是标题背景更换颜色等,加背景图片还是第一次遇到,大家可以先看下我的效果图是否与你遇到的问题一致! 首页标题的背景是个背景图片。 …...

必备工具:Postman Newman 详解
目录 Postman Newman 是什么? Postman Newman 的作用 如何使用 Postman Newman? 第一步:安装 Node.js 第二步:全局安装 Newman 第三步:导出集合或环境变量为 JSON 格式 第四步:使用 Newman 运行测试…...
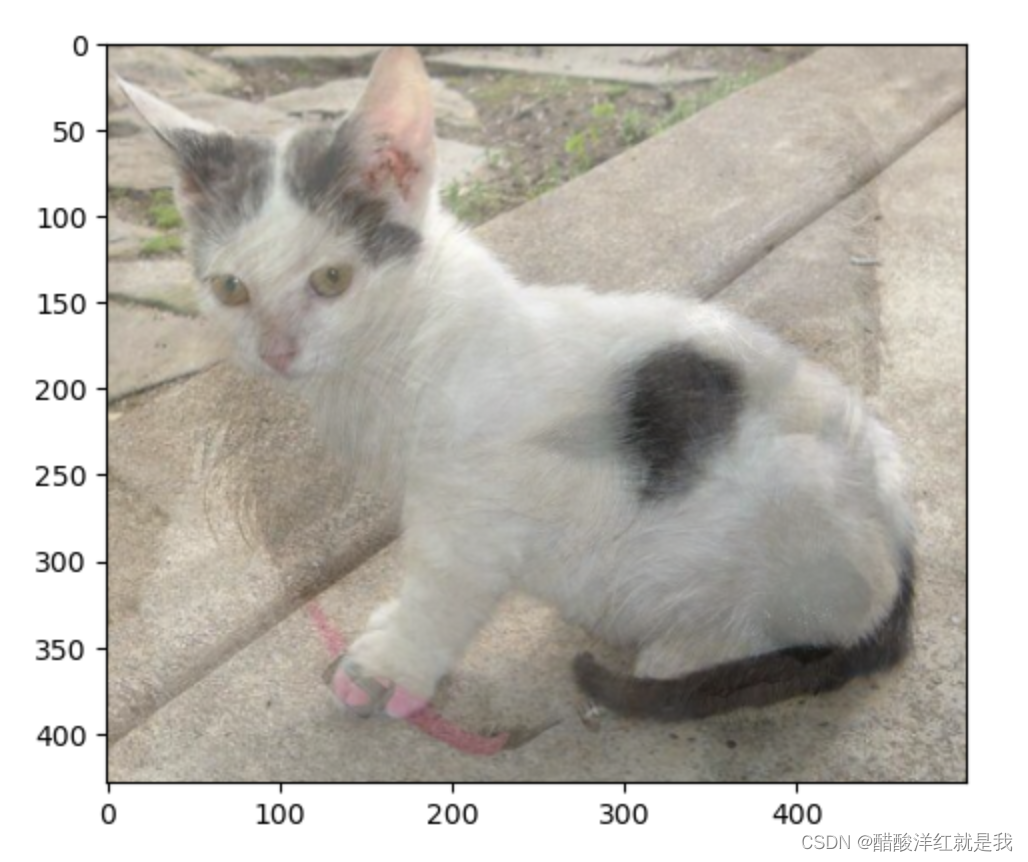
OpenCV基本操作——算数操作
目录 图像的加法图像的混合 图像的加法 两个图像应该具有相同的大小和类型,或者第二个图像可以是标量值 注意:OpenCV加法和Numpy加法之间存在差异。OpenCV的加法是饱和操作,而Numpy添加的是模运算 import numpy as np import cv2 as cv imp…...

css实现文字首行缩进的效果
<div class"content"><p>站在徐汇滨江西岸智塔45楼,波光粼粼的黄浦江一览无余。近处,是由龙华机场储油罐改造而来的油罐艺术中心和阿里巴巴上海总部办公处。远处,历史悠久的龙华塔挺拔秀丽,总投资逾600亿元…...
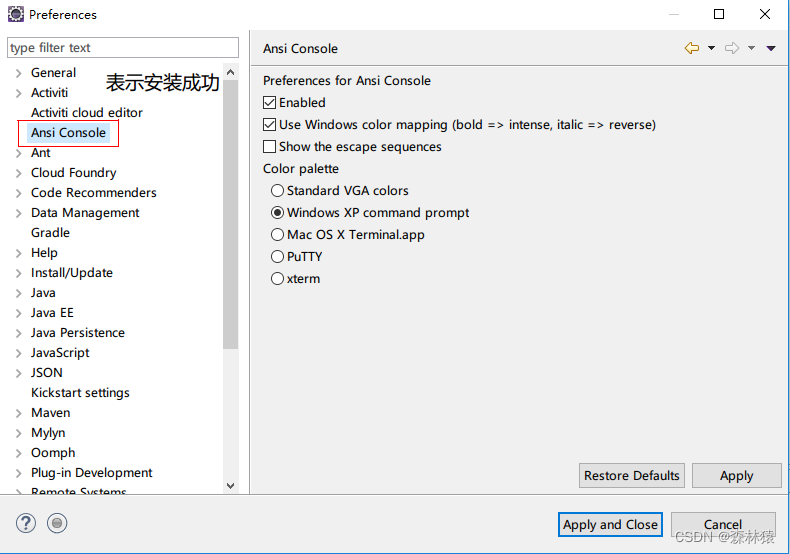
Eclipse-配置彩色输出打印
文章目录 前言配置下载查看是否安装 前言 这是一篇古老的文章,那个时候还在用Eclipse ,现在已经换 IDEA 了… 这是一篇 2018 年的文章,我只是将文章从个人比较挪到了CSDN 中 配置 配置完然后下载下面插件即可生成彩色代码。 下载 ANSI …...
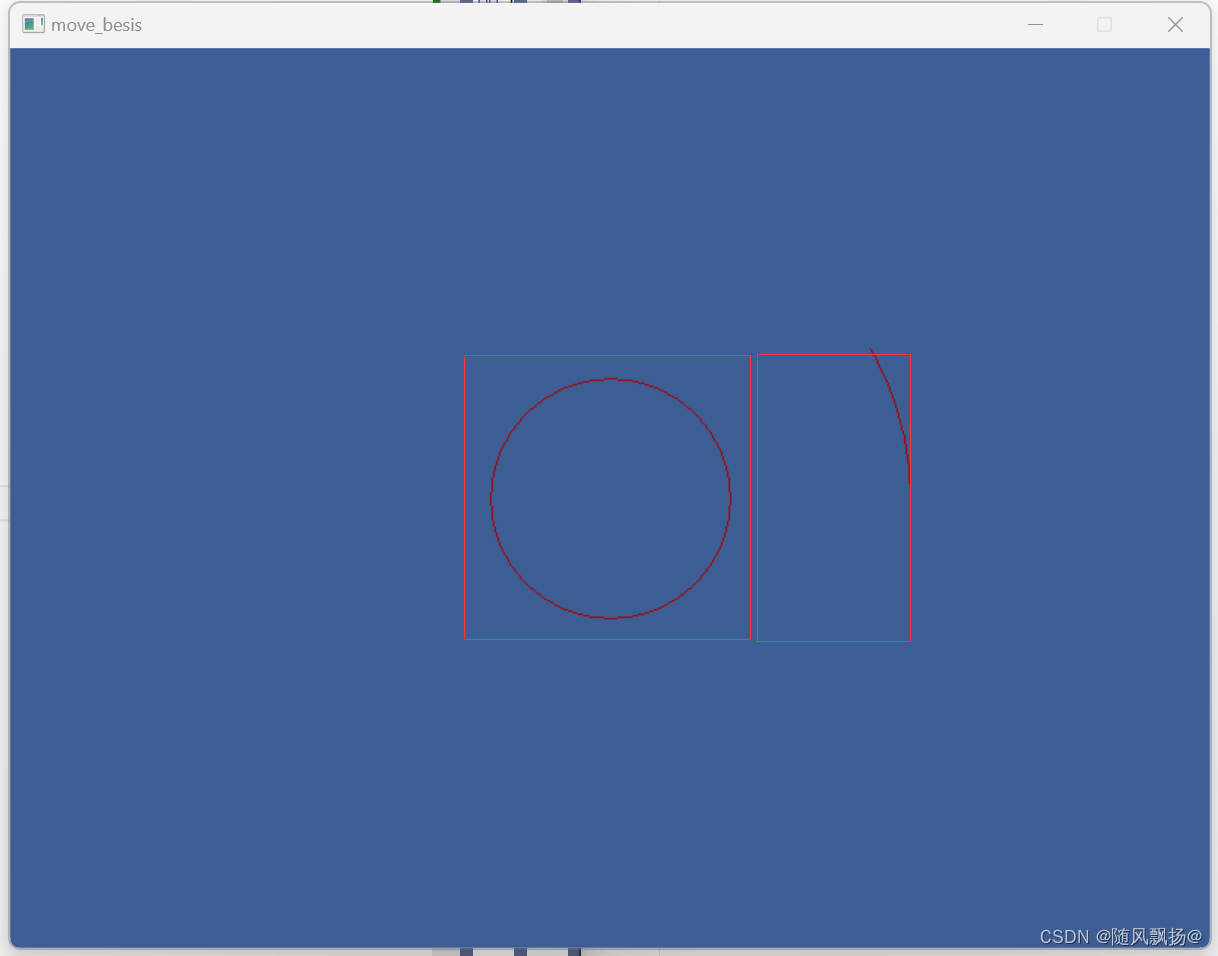
easyx图形库基础:1.基本概念的介绍+图形的绘制。
基本概念的介绍图形的绘制 一.基本概念的介绍。1.为什么要使用easyx图形库2.安装easyx图形库。3.语法相关 二.图形绘制1.窗体创建和坐标的概念。1.基本窗体的创建。2.坐标概念3.改变逻辑坐标。 2.设置图形颜色1.设置描边颜色和描边样式。2.设置图形填充颜色和填充样式3.绘制图形…...

zerotier requesting configuration
Q:zerotir无法获取physical ip A:路由器管理页面开启ipv6...
接口mock常用工具
在进行测试时,我们经常需要模拟接口数据,尤其是在前后端分离项目的开发中,在后端未完成开发时,前端拿不到后端的数据,就需要对后端返回的数据进行模拟。 如下一些工具,可以完成接口的mock。 Yapi 首先添…...

13-把矩阵看作是对系统的描述
探索矩阵乘法:更深刻的理解与应用视角 🧩🔍 引言 📖 在我们进一步探讨矩阵乘法之前,让我们从不同的角度来理解什么是矩阵,以及如何将矩阵视为一个系统。我们之前已经介绍了矩阵的基本概念和运算ÿ…...

Linux系统下安装Git软件
环境说明 Linux系统:CentOS 7.9 安装GCC等 JDK版本:jdk-8u202-linux-x64.tar.gz Maven版本:apache-maven-3.8.8-bin.tar.gz 在以上环境下安装Git(git-2.41.0.tar.gz)软件。 查看是否安装Git软件 查看Git版本&#…...
SpringBoot框架
一、SpringBoot概述 1. 简介 springboot是spring家族中的一个全新框架,用来简化spring程序的创建和开发过程。在以往我们通过SpringMVCSpringMybatis框架进行开发的时候,我们需要配置web.xml,spring配置,mybatis配置,…...
Chrome有些网站打不开,但是火狐可以打开
Chrome有些网站打不开,但是火狐可以打开 问题描述火狐成功界面谷歌报错界面局域网设置使用代理服务器访问成功 解决方案参考 问题描述 开了一个tizi,Chrome不能使用,火狐可以。之前装过插件Ghelper白嫖科学上网,那次之后好像浏览…...
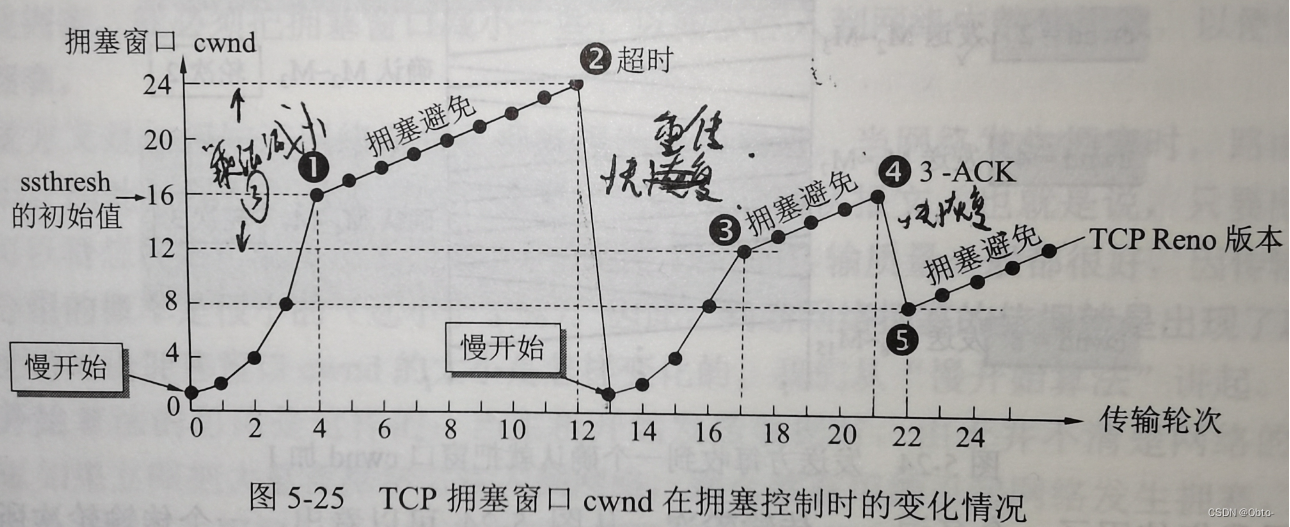
Linux网络基础(中)
目录: 再谈“协议” HTTP协议 认识URL: urlnecode和urldecode HTTP协议格式: HTTP的方法: 简易HTTP服务器: 传输层 再谈端口号: 端口号范围划分: netstat: pidof&…...
【C++起飞之路】初级—— auto、范围for循环、宏函数和内联函数
auto、范围for、内联函数、宏函数和nullptr 一、auto — 类型推导的魔法(C 11)1、auto 是什么?2、工作原理3、优势4、限制和注意事项 二、范围for (C11)1、基本语法2、优势3、工作原理4、注意事项5、C11: 范围 for 循环的扩展: 三…...

Chapter03-Authentication vulnerabilities
文章目录 1. 身份验证简介1.1 What is authentication1.2 difference between authentication and authorization1.3 身份验证机制失效的原因1.4 身份验证机制失效的影响 2. 基于登录功能的漏洞2.1 密码爆破2.2 用户名枚举2.3 有缺陷的暴力破解防护2.3.1 如果用户登录尝试失败次…...

springboot 百货中心供应链管理系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,百货中心供应链管理系统被用户普遍使用,为方…...

uni-app学习笔记二十二---使用vite.config.js全局导入常用依赖
在前面的练习中,每个页面需要使用ref,onShow等生命周期钩子函数时都需要像下面这样导入 import {onMounted, ref} from "vue" 如果不想每个页面都导入,需要使用node.js命令npm安装unplugin-auto-import npm install unplugin-au…...

STM32+rt-thread判断是否联网
一、根据NETDEV_FLAG_INTERNET_UP位判断 static bool is_conncected(void) {struct netdev *dev RT_NULL;dev netdev_get_first_by_flags(NETDEV_FLAG_INTERNET_UP);if (dev RT_NULL){printf("wait netdev internet up...");return false;}else{printf("loc…...

页面渲染流程与性能优化
页面渲染流程与性能优化详解(完整版) 一、现代浏览器渲染流程(详细说明) 1. 构建DOM树 浏览器接收到HTML文档后,会逐步解析并构建DOM(Document Object Model)树。具体过程如下: (…...

《C++ 模板》
目录 函数模板 类模板 非类型模板参数 模板特化 函数模板特化 类模板的特化 模板,就像一个模具,里面可以将不同类型的材料做成一个形状,其分为函数模板和类模板。 函数模板 函数模板可以简化函数重载的代码。格式:templa…...

智能AI电话机器人系统的识别能力现状与发展水平
一、引言 随着人工智能技术的飞速发展,AI电话机器人系统已经从简单的自动应答工具演变为具备复杂交互能力的智能助手。这类系统结合了语音识别、自然语言处理、情感计算和机器学习等多项前沿技术,在客户服务、营销推广、信息查询等领域发挥着越来越重要…...

Linux nano命令的基本使用
参考资料 GNU nanoを使いこなすnano基础 目录 一. 简介二. 文件打开2.1 普通方式打开文件2.2 只读方式打开文件 三. 文件查看3.1 打开文件时,显示行号3.2 翻页查看 四. 文件编辑4.1 Ctrl K 复制 和 Ctrl U 粘贴4.2 Alt/Esc U 撤回 五. 文件保存与退出5.1 Ctrl …...
)
【LeetCode】3309. 连接二进制表示可形成的最大数值(递归|回溯|位运算)
LeetCode 3309. 连接二进制表示可形成的最大数值(中等) 题目描述解题思路Java代码 题目描述 题目链接:LeetCode 3309. 连接二进制表示可形成的最大数值(中等) 给你一个长度为 3 的整数数组 nums。 现以某种顺序 连接…...

WebRTC调研
WebRTC是什么,为什么,如何使用 WebRTC有什么优势 WebRTC Architecture Amazon KVS WebRTC 其它厂商WebRTC 海康门禁WebRTC 海康门禁其他界面整理 威视通WebRTC 局域网 Google浏览器 Microsoft Edge 公网 RTSP RTMP NVR ONVIF SIP SRT WebRTC协…...
