Android核心开发之——OpenGL
OpenGL是一种用于编程计算机图形的应用程序编程接口(API)。它提供了一系列函数和方法,用于绘制2D和3D图形,以及进行渲染和图形处理。OpenGL可以跨平台使用,支持各种操作系统和硬件设备。它被广泛应用于游戏开发、虚拟现实、科学可视化、计算机辅助设计等领域。OpenGL具有高性能、灵活性和可扩展性的特点,可以利用图形硬件的加速功能,实现快速而逼真的图形渲染。
OpenGL的简单使用与解析
以下是一个简单的OpenGL使用代码示例,用于创建一个窗口并绘制一个彩色三角形:
#include <GL/glew.h>
#include <GLFW/glfw3.h>
void framebuffer_size_callback(GLFWwindow* window, int width, int height)
{glViewport(0, 0, width, height);
}
int main()
{// 初始化GLFWglfwInit();glfwWindowHint(GLFW_CONTEXT_VERSION_MAJOR, 3);glfwWindowHint(GLFW_CONTEXT_VERSION_MINOR, 3);glfwWindowHint(GLFW_OPENGL_PROFILE, GLFW_OPENGL_CORE_PROFILE);
// 创建窗口对象GLFWwindow* window = glfwCreateWindow(800, 600, "OpenGL Window", NULL, NULL);if (window == NULL){glfwTerminate();return -1;}glfwMakeContextCurrent(window);
// 初始化GLEW if (glewInit() != GLEW_OK){return -1;}
// 设置视口大小 int width, height;glfwGetFramebufferSize(window, &width, &height);glViewport(0, 0, width, height);glfwSetFramebufferSizeCallback(window, framebuffer_size_callback);
// 定义顶点数据 float vertices[] = {-0.5f, -0.5f, 0.0f,0.5f, -0.5f, 0.0f,0.0f, 0.5f, 0.0f };
// 创建顶点缓冲对象 unsigned int VBO;glGenBuffers(1, &VBO);glBindBuffer(GL_ARRAY_BUFFER, VBO);glBufferData(GL_ARRAY_BUFFER, sizeof(vertices), vertices, GL_STATIC_DRAW);
// 创建顶点数组对象 unsigned int VAO;glGenVertexArrays(1, &VAO);glBindVertexArray(VAO);glVertexAttribPointer(0, 3, GL_FLOAT, GL_FALSE, 3 * sizeof(float), (void*)0);glEnableVertexAttribArray(0);
// 渲染循环 while (!glfwWindowShouldClose(window)){// 输入处理 glfwPollEvents();
// 渲染指令 glClearColor(0.2f, 0.3f, 0.3f, 1.0f);glClear(GL_COLOR_BUFFER_BIT);
// 绘制三角形glBindVertexArray(VAO);glDrawArrays(GL_TRIANGLES, 0, 3);
// 交换缓冲区glfwSwapBuffers(window);}
// 清理资源glDeleteVertexArrays(1, &VAO);glDeleteBuffers(1, &VBO);glfwTerminate();return 0;
}
代码解析:
- 引入必要的头文件:glew.h 和 glfw3.h。
- 定义回调函数 framebuffer_size_callback,用于处理窗口大小变化时的事件。
- 在 main 函数中,初始化 GLFW,设置 OpenGL 版本和配置窗口属性。
- 创建窗口对象,并检查是否创建成功。
- 设置当前上下文为窗口的上下文。
- 初始化 GLEW。
- 获取窗口的帧缓冲大小,并设置视口大小。并设置窗口大小变化时的回调函数。
- 定义顶点数据,这里定义了一个简单的三角形。
- 创建顶点缓冲对象(VBO)并将顶点数据绑定到缓冲区。
- 创建顶点数组对象(VAO)并配置顶点属性指针。
- 进入渲染循环,判断窗口是否需要关闭。
- 处理输入事件,例如键盘输入。
- 清空颜色缓冲区。
- 绑定顶点数组对象和绘制指令,绘制三角形。
- 交换前后缓冲区,更新窗口显示。
- 清理资源,删除顶点数组对象和顶点缓冲对象。
- 终止 GLFW,释放所有的资源。
演示了一个最基本的OpenGL使用流程,包括初始化OpenGL环境、创建窗口、设置视口、创建顶点缓冲区和顶点数组对象、渲染循环以及清理资源等。你可以根据自己的需求,进一步扩展和修改代码,添加纹理映射、光照效果等,实现更复杂的图形渲染。本文主要简单解析了在Android开发中OpenGL技术使用,更多有关Android开发的核心技术可以参考《Android核心技术手册》点击可查看详细类目。
最后
OpenGL是一个跨平台的图形编程接口,用于实现2D和3D图形的渲染和处理。它提供了一系列函数和状态机来操作图形硬件,使开发者能够创建各种复杂的图形效果和交互式应用程序。OpenGL仅仅提供了底层的图形操作接口,开发者需要具备一定的图形学知识和编程技巧,才能充分利用OpenGL的功能。
相关文章:

Android核心开发之——OpenGL
OpenGL是一种用于编程计算机图形的应用程序编程接口(API)。它提供了一系列函数和方法,用于绘制2D和3D图形,以及进行渲染和图形处理。OpenGL可以跨平台使用,支持各种操作系统和硬件设备。它被广泛应用于游戏开发、虚拟现…...

公共服务领域:西安新小区业主自立业主委员会年底分红83万以及103万事件区块链资金透明监管与投票解决方案的尝试
公共服务领域:西安新小区业主自立业主委员会年底分红83万以及103万事件区块链资金透明监管与投票解决方案的尝试 作者 重庆电子工程职业学院 | 向键雄 杜小敏 前言 本项目想法来源于,西安新小区业主开出物业自立业主委员会年底分红83万以及103万事件,对于此类事件,我们刨…...

ID3 决策树
西瓜数据集D如下: 编号色泽根蒂敲声纹理脐部触感好瓜1青绿蜷缩浊响清晰凹陷硬滑是2乌黑蜷缩沉闷清晰凹陷硬滑是3乌黑蜷缩浊响清晰凹陷硬滑是4青绿蜷缩沉闷清晰凹陷硬滑是5浅白蜷缩浊响清晰凹陷硬滑是6青绿稍蜷浊响清晰稍凹软粘是7乌黑稍蜷浊响稍糊稍凹软粘是8乌黑稍蜷浊响清晰…...

简单线性回归:预测事物间简单关系的利器
文章目录 🍀简介🍀什么是简单线性回归?🍀简单线性回归的应用场景使用步骤:注意事项: 🍀代码演示🍀结论 🍀简介 在数据科学领域,线性回归是一种基本而强大的统…...
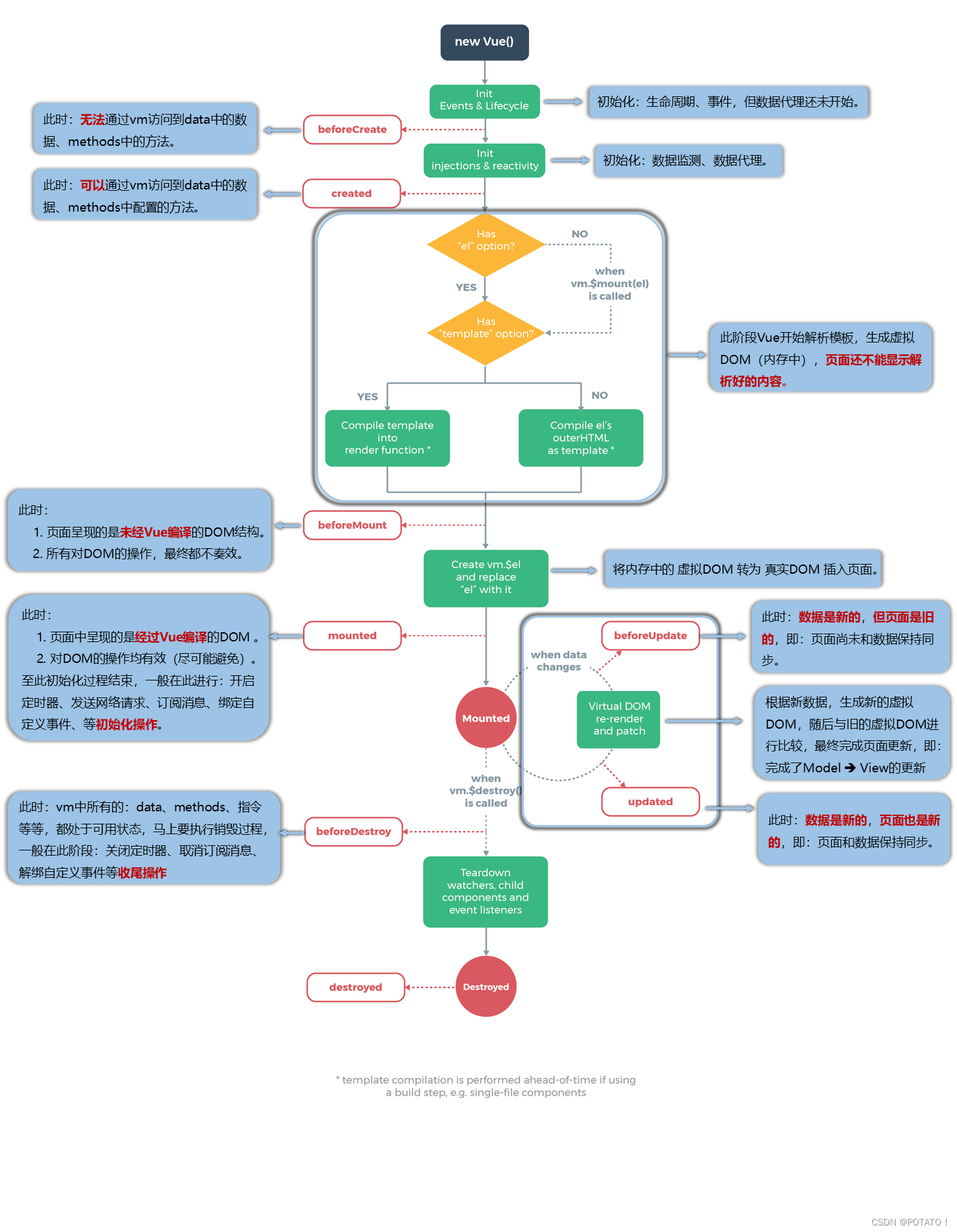
Vue2-收集表单数据、过滤器、内置指令与自定义指令、Vue生命周期
🥔:我徒越万重山 千帆过 万木自逢春 更多Vue知识请点击——Vue.js VUE2-Day4 收集表单数据1、不同标签的value属性2、v-model的三个修饰符 过滤器内置指令与自定义指令1、内置指令2、自定义指令定义语法(1)函数式(2&am…...

正则表达式学习详解
正则表达式 正则表达式(Regular Expression),通常简称为正则或正则表达式,是一种用于描述字符串模式的工具。它是由一系列字符和特殊字符组成的字符串,用于定义搜索模式或进行字符串匹配、替换、提取等操作。 正则表…...
)
工具箱:在线免费使用的文档工具:(PDF转换,图片压缩等)
这些都是博主亲自使用过的,可以使用。 PDF转换器: http://www.pdfdo.com/ 图片压缩: 免费在线图片/视频压缩工具 | 图片压缩 | 免费 JPG PNG GIF 图像压缩 (yalijuda.com) 文档OCR转EXCEL: 文字识别 OCR_ 图片文字识别_图片文字智能识别…...
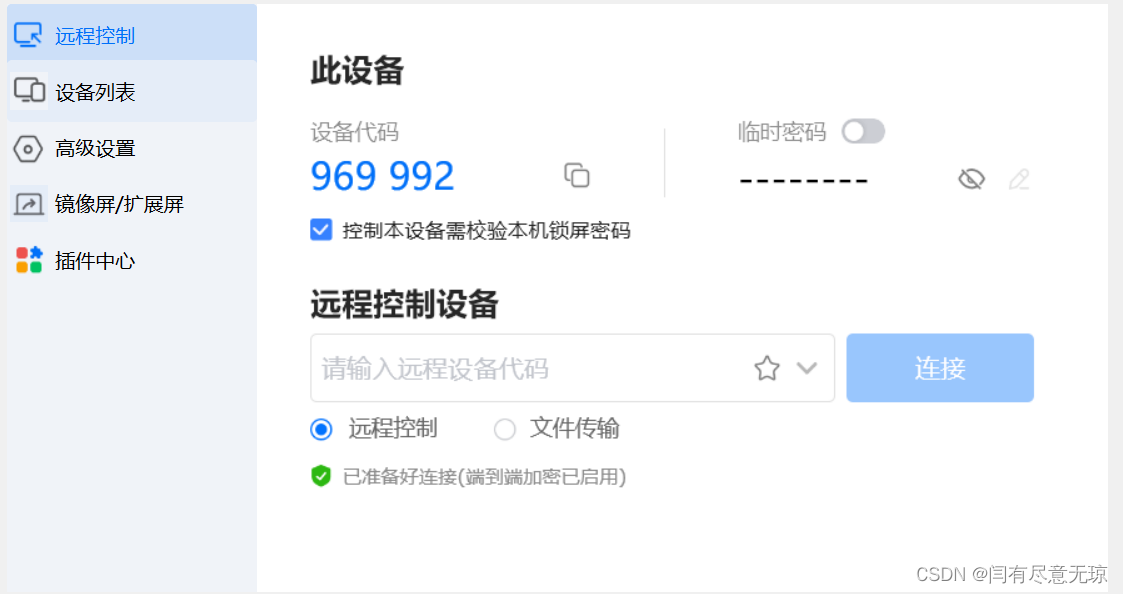
Qt6之QStackedWidget——Qt仿ToDesk(2)
一、 QStackedWidget概述 QStackedWidget也叫堆栈窗体类,它继承于QFrame,主要与QListWidget等结合使用,实现“一个界面多个页面切换”。 二、QStackedWidget示例 如下图,当点击左边 QListWidget里的菜单时,右边跟随切…...
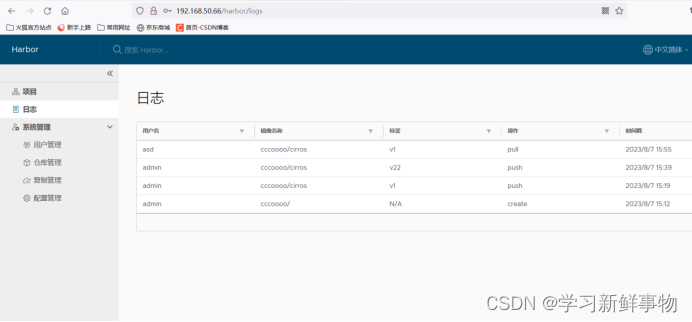
Harbor企业镜像仓库部署(本地)
简述: Docker 官方镜像仓库是用于管理公共镜像的地方,大家可以在上面找到想要的镜像,也可以把自己的镜像推送上去。但是有时候服务器无法访问互联网,或者不希望将自己的镜像放到互联网上,那么就需要用到 Docker Regis…...

【Linux】如何打包成动静态库,第三方动静态库如何使用?
文章目录 1. 打包成静态库2. 打包成动态库(共享库)3. 使用第三方静态库4. 使用第三方动态库 5. 动态库的加载6. 注意事项 库的名称:去掉前面的 lib 去掉后面的 .a(版本号) .so(版本号) 剩下的,才是库正真的名称。 查看文件依赖库…...

SAP MM学习笔记20- SAP中的英文2 - SD中英文,日语,中文
SD模块中的英文,日语,中文 对照。 販売管理 日本語英語中国語受注伝票sales order销售订单出荷伝票delivery order交货订单ピッキングリストpicking list领货清单シップメント伝票shipment document发运单据出庫確認post goods issue发货确认請求伝票b…...

计算机网络中的一些基本概念
IP地址: 址用于定位主机的网络地址。是一个32位的二进制数,通常被分割为4个“8位二进制数”(也就是4个字节).**端口号:**在网络通信中,IP地址用于标识主机网络地址,端口号可以标识主机中发送数据、接收数据的进程。简单…...

pytest 用例运行方式
一、命令行方式运行 执行某个目录下所有的用例,符合规范的所有用例 进入到对应的目录,直接执行pytest; 例如需要执行testcases 下的所有用例; 可以进入testcases 目录; 然后执行pytest 进入对应目录的上级目录,执行pytest 目录名称/ ; ; 例如需要执行testcases 下…...

简单入门seleniumUI自动化测试
目录 一、selenium的介绍 二、selenium的原理 三、selenium的八种元素定位的方法 1、ID定位: 2 、name定位: 3、class定位: 4、tag定位: 5、link_text定位: 6、partial_link_text定位: 7、css定位…...

Excel(1):表头或列头冻结
1.需求 对于较大的excel,通常需要固定一部分内容,另一份内容为可翻动。 2.解决方式 在视图中选择冻结窗格,需要注意的是,选择冻结窗格时,窗格的左上方的表格区域是固定不动的,只可以向下或者向右活动。...
通达OA SQL注入漏洞【CVE-2023-4166】
通达OA SQL注入漏洞【CVE-2023-4166】 一、产品简介二、漏洞概述三、影响范围四、复现环境POC小龙POC检测工具: 五、修复建议 免责声明:请勿利用文章内的相关技术从事非法测试,由于传播、利用此文所提供的信息或者工具而造成的任何直接或者间接的后果及损…...
全网最细,Python接口自动化测试-Session会话保持(实战详细)
目录:导读 前言一、Python编程入门到精通二、接口自动化项目实战三、Web自动化项目实战四、App自动化项目实战五、一线大厂简历六、测试开发DevOps体系七、常用自动化测试工具八、JMeter性能测试九、总结(尾部小惊喜) 前言 在接口测试的过程…...

Java项目初始化ES、MYSQL表结构及表数据
一、初始化MYSQL数据 public boolean initMysql() throws Exception {log.info("initMysql.start");//获取所连接的数据库名称String database systemMapper.getDatabase();if (StringUtils.isBlank(database)) {throw new BusinessException("连接数据库失败,…...

2023-08-13力扣每日一题
链接: 88. 合并两个有序数组 题意: 如题 解: 从后往前(从大到小)插入排序,这样就不会影响原先的有序性 实际代码: #include<bits/stdc.h> using namespace std; void merge(vector…...
下一代深度学习的思考与若干问题
下一代深度学习的思考和若干问题...

C++实现分布式网络通信框架RPC(3)--rpc调用端
目录 一、前言 二、UserServiceRpc_Stub 三、 CallMethod方法的重写 头文件 实现 四、rpc调用端的调用 实现 五、 google::protobuf::RpcController *controller 头文件 实现 六、总结 一、前言 在前边的文章中,我们已经大致实现了rpc服务端的各项功能代…...

线程与协程
1. 线程与协程 1.1. “函数调用级别”的切换、上下文切换 1. 函数调用级别的切换 “函数调用级别的切换”是指:像函数调用/返回一样轻量地完成任务切换。 举例说明: 当你在程序中写一个函数调用: funcA() 然后 funcA 执行完后返回&…...

UE5 学习系列(三)创建和移动物体
这篇博客是该系列的第三篇,是在之前两篇博客的基础上展开,主要介绍如何在操作界面中创建和拖动物体,这篇博客跟随的视频链接如下: B 站视频:s03-创建和移动物体 如果你不打算开之前的博客并且对UE5 比较熟的话按照以…...

OkHttp 中实现断点续传 demo
在 OkHttp 中实现断点续传主要通过以下步骤完成,核心是利用 HTTP 协议的 Range 请求头指定下载范围: 实现原理 Range 请求头:向服务器请求文件的特定字节范围(如 Range: bytes1024-) 本地文件记录:保存已…...

EtherNet/IP转DeviceNet协议网关详解
一,设备主要功能 疆鸿智能JH-DVN-EIP本产品是自主研发的一款EtherNet/IP从站功能的通讯网关。该产品主要功能是连接DeviceNet总线和EtherNet/IP网络,本网关连接到EtherNet/IP总线中做为从站使用,连接到DeviceNet总线中做为从站使用。 在自动…...

Unit 1 深度强化学习简介
Deep RL Course ——Unit 1 Introduction 从理论和实践层面深入学习深度强化学习。学会使用知名的深度强化学习库,例如 Stable Baselines3、RL Baselines3 Zoo、Sample Factory 和 CleanRL。在独特的环境中训练智能体,比如 SnowballFight、Huggy the Do…...

微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据
微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据 Power Query 具有大量专门帮助您清理和准备数据以供分析的功能。 您将了解如何简化复杂模型、更改数据类型、重命名对象和透视数据。 您还将了解如何分析列,以便知晓哪些列包含有价值的数据,…...

使用Matplotlib创建炫酷的3D散点图:数据可视化的新维度
文章目录 基础实现代码代码解析进阶技巧1. 自定义点的大小和颜色2. 添加图例和样式美化3. 真实数据应用示例实用技巧与注意事项完整示例(带样式)应用场景在数据科学和可视化领域,三维图形能为我们提供更丰富的数据洞察。本文将手把手教你如何使用Python的Matplotlib库创建引…...

免费PDF转图片工具
免费PDF转图片工具 一款简单易用的PDF转图片工具,可以将PDF文件快速转换为高质量PNG图片。无需安装复杂的软件,也不需要在线上传文件,保护您的隐私。 工具截图 主要特点 🚀 快速转换:本地转换,无需等待上…...

在Mathematica中实现Newton-Raphson迭代的收敛时间算法(一般三次多项式)
考察一般的三次多项式,以r为参数: p[z_, r_] : z^3 (r - 1) z - r; roots[r_] : z /. Solve[p[z, r] 0, z]; 此多项式的根为: 尽管看起来这个多项式是特殊的,其实一般的三次多项式都是可以通过线性变换化为这个形式…...
