贪心算法:基础入门篇
贪心算法:基础入门篇
文章目录:
- 贪心算法:基础入门篇
- 一、认识贪心算法
- 二、常见贪心问题
- 2.1 纸牌问题
- 2.2 背包问题(基础版)
- 2.3 简单数学证明问题
- 三、总结
一、认识贪心算法
在求最优解的问题中,以某种贪心标准,从状态的最初始找到每一步最优解,通过多次的贪心求解,最终得到整个问题的最优解,此种解题的方法为贪心算法。可见贪心算法并不是一种固定的算法,而是根据问题的条件而产生的一种解决问题的思维模式。
由定义可知,贪心算法是由局部的最优解,得到总体的最优解,因此在使用贪心算法之前,要先判断问题是否适合使用贪心算法。
二、常见贪心问题
2.1 纸牌问题
纸牌问题是最简单,也最好理解的贪心问题,题目如下:
题目描述:
有 N N N 堆纸牌,编号分别为 1 , 2 , … , N 1,2,\ldots,N 1,2,…,N。每堆上有若干张,但纸牌总数必为 N N N 的倍数。可以在任一堆上取若干张纸牌,然后移动。
移牌规则为:在编号为 1 1 1 堆上取的纸牌,只能移到编号为 2 2 2 的堆上;在编号为 N N N 的堆上取的纸牌,只能移到编号为 N − 1 N-1 N−1 的堆上;其他堆上取的纸牌,可以移到相邻左边或右边的堆上。
现在要求找出一种移动方法,用最少的移动次数使每堆上纸牌数都一样多。
例如 N = 4 N=4 N=4 时, 4 4 4 堆纸牌数分别为 9 , 8 , 17 , 6 9,8,17,6 9,8,17,6。
移动 3 3 3 次可达到目的:
- 从第三堆取 4 4 4 张牌放到第四堆,此时每堆纸牌数分别为 9 , 8 , 13 , 10 9,8,13,10 9,8,13,10。
- 从第三堆取 3 3 3 张牌放到第二堆,此时每堆纸牌数分别为 9 , 11 , 10 , 10 9,11,10,10 9,11,10,10。
- 从第二堆取 1 1 1 张牌放到第一堆,此时每堆纸牌数分别为 10 , 10 , 10 , 10 10,10,10,10 10,10,10,10。
输入格式:
第一行共一个整数 N N N,表示纸牌堆数。
第二行共 N N N 个整数 A 1 , A 2 , … , A N A_1,A_2,\ldots,A_N A1,A2,…,AN,表示每堆纸牌初始时的纸牌数。
输出格式:
共一行,即所有堆均达到相等时的最少移动次数。
样例:
样例输入
4
9 8 17 6
样例输出
3
提示
对于 100 % 100\% 100% 的数据, 1 ≤ N ≤ 100 1 \le N \le 100 1≤N≤100, 1 ≤ A i ≤ 10000 1 \le A_i \le 10000 1≤Ai≤10000。
【题目来源】
NOIP 2002 提高组第一题
题目解析:
根据移牌规则,可以得出以下通式:
{ a i > a v e , a i + 1 = ( a i − a v e ) + a i + 1 a i = a v e a i < a v e , a i + 1 = a i + 1 − ( a v e − a i ) \left\{\begin{matrix}a_i> ave,a_{i+1}=(a_i-ave)+a_{i+1}\\a_i=ave \\a_i< ave,a_{i+1}=a_{i+1}-(ave-a_i)\end{matrix}\right. ⎩ ⎨ ⎧ai>ave,ai+1=(ai−ave)+ai+1ai=aveai<ave,ai+1=ai+1−(ave−ai)
在左至右开始排列的情况下,从移牌规则中可得知,大于平均数的牌只能向左移动,反之小于平均数的牌只能向右移动。由此可以画出以下关系图:
#include <iostream>
using namespace std;
int main(){int a,sum=0,ave=0;int b[100];cin>>a;for(int i=0;i<a;i++){cin>>b[i];ave+=b[i];}ave=ave/a;for(int i=0;i<a;i++){if(b[i]>ave){b[i+1]+=b[i]-ave;sum++;}if(ave>b[i]){b[i+1]=b[i+1]-(ave-b[i]);sum++;}}cout<<sum;return 0;
}
2.2 背包问题(基础版)
背包问题是贪心算法中比较经典的贪心问题,同时背包问题也是一个经典的动态规划问题,其基本形式是:给定一个背包,容量为C,和一组物品,每个物品有自己的重量和价值,现在从这些物品中选择一些装入背包,要求背包中物品的总重量不超过C,且总价值最大。
接下来以一个题目来进行讲解:
题目描述
阿里巴巴走进了装满宝藏的藏宝洞。藏宝洞里面有 N ( N ≤ 100 ) N(N \le 100) N(N≤100) 堆金币,第 i i i 堆金币的总重量和总价值分别是 m i , v i ( 1 ≤ m i , v i ≤ 100 ) m_i,v_i(1\le m_i,v_i \le 100) mi,vi(1≤mi,vi≤100)。阿里巴巴有一个承重量为 T ( T ≤ 1000 ) T(T \le 1000) T(T≤1000) 的背包,但并不一定有办法将全部的金币都装进去。他想装走尽可能多价值的金币。所有金币都可以随意分割,分割完的金币重量价值比(也就是单位价格)不变。请问阿里巴巴最多可以拿走多少价值的金币?
输入格式
第一行两个整数 N , T N,T N,T。
接下来 N N N 行,每行两个整数 m i , v i m_i,v_i mi,vi。
输出格式
一个实数表示答案,输出两位小数
样例
样例输入
4 50
10 60
20 100
30 120
15 45
样例输出 #1
240.00
【题目来源】
洛谷 P2240 【深基12.例1】部分背包问题
题目解析:
根据题目可知,金币堆可以拆分,并将价值最大的情况带走。对于此题,我们需求出每堆金币的单价,找出单价最高的,然后依次搜索,到背包装满。
根据此流程图可写出代码:
#include <iostream>
#include <iomanip>
using namespace std;
int main() {int n, t;float money=0;float a[100][3];cin >> n >> t;for (int i = 0; i < n; i++)for (int j = 0; j < 2; j++) {cin >> a[i][j];a[i][2] = a[i][1] / a[i][0];}
to:float max = 0;int max_num;for (int i = 0; i < n; i++) {if (max < a[i][2]) {max = a[i][2];max_num = i;}}if (t <= a[max_num][0]) {money += t * max;}else {money += a[max_num][0] * max;t = t - a[max_num][0];a[max_num][2] = 0;goto to;}cout << fixed << setprecision(2) << money;return 0;
}
2.3 简单数学证明问题
在数学问题中,存在多分支的情况下,不知道最优解时,可用贪心算法找出最优解。
题目描述
有 n n n 个人在一个水龙头前排队接水,假如每个人接水的时间为 T i T_i Ti,请编程找出这 n n n 个人排队的一种顺序,使得 n n n 个人的平均等待时间最小。
输入格式
第一行为一个整数 n n n。
第二行 n n n 个整数,第 i i i 个整数 T i T_i Ti 表示第 i i i 个人的等待时间 T i T_i Ti。
输出格式
输出文件有两行,第一行为一种平均时间最短的排队顺序;第二行为这种排列方案下的平均等待时间(输出结果精确到小数点后两位)。
样例
样例输入
10
56 12 1 99 1000 234 33 55 99 812
样例输出
3 2 7 8 1 4 9 6 10 5
291.90
提示
1 ≤ n ≤ 1000 1\le n \leq 1000 1≤n≤1000, 1 ≤ t i ≤ 1 0 6 1\le t_i \leq 10^6 1≤ti≤106,不保证 t i t_i ti 不重复。
【题目来源】
洛谷 P1223 排队接水
题目解析:
根据题目可知道,要让平均等待时长最少,就需要将总等待时长控制在最小,因此需要将用时最短的人,最先安排接水,就可以得到最短总时长。数学表达式如下:
f m i n _ t i m e ( x ) = ∑ i = 1 n ( n − i ) T i f_{min\_time}(x)= \sum_{i=1}^{n} (n-i)T_i fmin_time(x)=i=1∑n(n−i)Ti
此题通过简单的排序算法,即可解决。代码如下:
#include <iostream>
#include <iomanip>
using namespace std;
int main() {double t = 0;int n;int a[1001][2];cin >> n;for (int i = 1; i <= n; i++) {cin >> a[i][0];a[i][1] = i;}for (int i = 1; i <= n ; i++) {for (int j = 1; j <= n - i; j++) {if (a[j][0] > a[j + 1][0]) {int temp = a[j + 1][0];a[j+1][0] = a[j][0];a[j][0] = temp;int temp1 = a[j + 1][1];a[j+1][1] = a[j][1];a[j][1] = temp1;}}}for (int i = 1; i <= n; i++) {cout << a[i][1] << ' ';t += (n - i) * a[i][0];}t = t / n;cout << fixed << setprecision(2) <<endl <<t;
}
三、总结
贪心算法所作的选择来源于以往的选择,并非将来的选择。贪心算法相对于其他算法有一定的速度优势,在一题可以多解的情况下,可以优先选择贪心算法。
相关文章:

贪心算法:基础入门篇
贪心算法:基础入门篇 文章目录: 贪心算法:基础入门篇一、认识贪心算法二、常见贪心问题2.1 纸牌问题2.2 背包问题(基础版)2.3 简单数学证明问题 三、总结 一、认识贪心算法 在求最优解的问题中,以某种贪心…...

【Windows10下启动RocketMQ报错:找不到或无法加载主类 Files\Java\jdk1.8.0_301\lib\dt.jar】解决方法
Windows10下启动RocketMQ报错:找不到或无法加载主类 一、问题产生二、产生原因三、解决办法 一、问题产生 参考RocketMQ Github官网上的说明,下载rocketmq-all-5.1.3-bin-release.zip,解压配置环境变量后,执行如下命令:…...
深入篇【Linux】学习必备:进程理解(从底层探究进程概念/进程创建/进程状态/进程优先级)
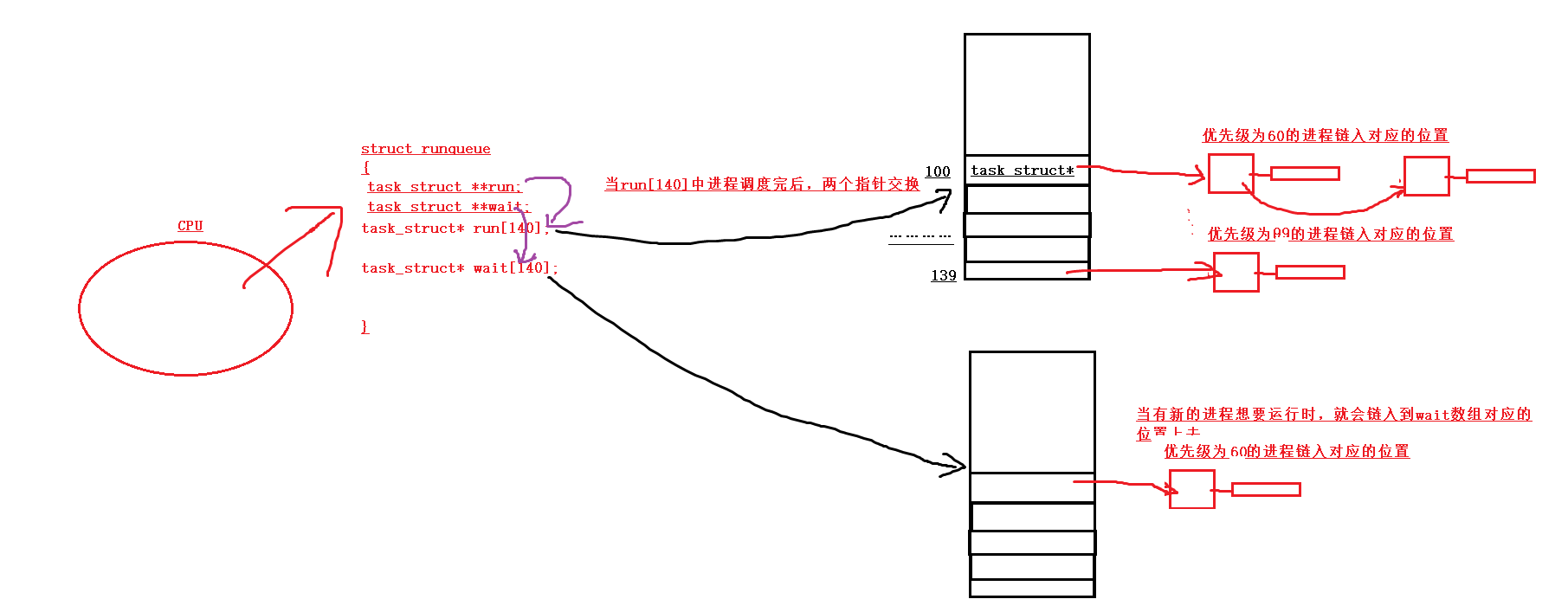
深入篇【Linux】学习必备:进程理解(从底层探究进程概念/进程创建/进程状态/进程优先级) 一.进程概念(PCB/task_struct)二.查看进程(top/ps)三.创建进程(fork)四.进程状态(僵尸进程/孤儿进程)五.进程优先级(PRI/NI) 一.进程概念(PCB/task_struct) 1.什么…...
Python 潮流周刊#15:如何分析 FastAPI 异步请求的性能?
你好,我是猫哥。这里每周分享优质的 Python、AI 及通用技术内容,大部分为英文。标题取自其中一则分享,不代表全部内容都是该主题,特此声明。 本周刊精心筛选国内外的 250 信息源,为你挑选最值得分享的文章、教程、开源…...

基于Java+SpringBoot+Vue的网吧管理系统设计与实现(源码+LW+部署文档等)
博主介绍: 大家好,我是一名在Java圈混迹十余年的程序员,精通Java编程语言,同时也熟练掌握微信小程序、Python和Android等技术,能够为大家提供全方位的技术支持和交流。 我擅长在JavaWeb、SSH、SSM、SpringBoot等框架…...

redis设置database 不生效剖析
设置database 不生效剖析 前言配置加载类问题commons-pool 对象池 主页传送门:📀 传送 前言 事情是这样的 今天在拉取了同事的代码做redis缓存设置的时候,发现即使已经设置了database, 但是存数据的时候还是用的默认0数据库。这引起了我的好…...
汽车及汽车零部件行业云MES解决方案
汽配行业现状: 随着经济全球化进程加快,一直走在智能化改造,数字化转型前沿的汽车行业企业,面临的信息化需求也日益增加,不管德系,美系还是日系供应链的各大厂商,均将企业信息化,数字…...
)
算法工程师-机器学习面试题总结(4)
深度学习 DNN 描述一下神经网络?推导反向传播公式? 神经网络(Neural Network)是一种模拟人脑神经系统的计算模型。它由许多节点(神经元)和连接它们的权重组成,这些节点和权重可以学习和调整&a…...

Linux学习之awk函数
awk里边的函数分为内置函数和自定义函数。 内置函数有下边的几种: 算术函数(arithmetic) 字符串函数(string) 输入/输出函数和通用函数(input/output, and general) 自定义函数格式如下…...

Redis的数据结构到底是一种什么样的结构?
有了上一篇NoSQL的基础,我们也都知道了Redis就是一种典型的NoSql,那我们就先简简单单的介绍一下Redis: Redis是什么? Redis(Remote Dictionary Server)是一个开源的使用ANSI C语言编写的高性能键值存储系统…...
eclipse 导入项目js报错问题
eclipse 导入项目后会出现项目中的js文件报错(红叉),如下图所示,有时候报错的文件很多,需要集中处理。 解决办法: 右键项目名称》Properties》MyEclipse》JavaScript》Include Path,在右侧选择“…...
《HeadFirst设计模式(第二版)》第七章代码——外观模式
代码文件目录: Subsystem: Amplifier package Chapter7_AdapterAndFacadePattern.FacadePattern.Subsystem;/*** Author 竹心* Date 2023/8/8**///扬声器 public class Amplifier {int volume 0;//音量public void on(){System.out.println("The amplifier …...

前端杂项-个人总结八股文的背诵方案
个人总结八股文的背诵方案 URL到显示网页的过程 浏览器解析URL,获取协议,主机名,端口号,路径等信息,并通过DNS查询将主机名转换为对应的IP地址浏览器与服务器建立TCP,进行三次握手。浏览器向服务器发送HT…...

利用 3D 地理空间数据实现Cesium的沉浸式环境
推荐:使用 NSDT场景编辑器 助你快速搭建可编辑的3D应用场景 为了将大量异构 3D 地理空间数据处理和分散到各行各业的地理空间应用程序和运行时引擎,Cesium 创建了 3D Tiles,这是一种用于高效流式传输和渲染大量异构数据集的开放标准。3D Tile…...

微服务——ES实现自动补全
效果展示 在搜索框根据拼音首字母进行提示 拼音分词器 和IK中文分词器一样的用法,按照下面的顺序执行。 # 进入容器内部 docker exec -it elasticsearch /bin/bash# 在线下载并安装 ./bin/elasticsearch-plugin install https://github.com/medcl/elasticsearch…...

北斗+5G 织就精确定位的“天罗地网”
今年,邓中亮更忙了。 外部会议,内部讨论,课题研究,还有疫情困扰期间没能出的差铆足劲似的补上,一天里,从离开床和回到床中间的时间都被工作冠名了。 北京邮电大学教授邓中亮 忙碌的加速键在2020年按下暂停…...

Ansible Roles详解
Ansible 的角色(Roles)是一种组织和管理任务和变量的方法,可以帮助您更好地组织和重用 Ansible 代码。角色是一个可重用的、自包含的 Ansible 单元,它封装了一组任务和变量,可以在不同的剧本中轻松地重用。 角色的目录…...
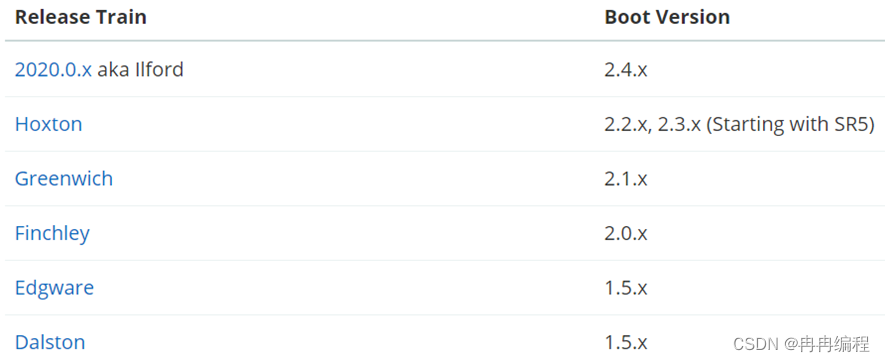
微服务学习笔记-基本概念
微服务是一种经过良好架构设计的分布式架构方案。根据业务功能对系统做拆分,每个业务功能模块作为独立项目开发,称为一个服务。 微服务的架构特征: 单一职责:微服务拆分粒度更小,每一个服务都对应唯一的业务能力&…...

Linux查看GPU显卡/CPU内存/硬盘信息
显卡信息命令/CPU内存/硬盘 1.显卡2、CPU内存3、硬盘 1.显卡 nvidia-smi nvidia-smi(显示一次当前GPU占用情况) nvidia-smi -l(每秒刷新一次并显示) watch -n 5 nvidia-smi (其中,5表示每隔6秒刷新一次终端…...

SQLAlchemy 入门:Python 中的 SQL 工具包和 ORM
SQLAlchemy 是 Python 中一款非常流行的数据库工具包,它对底层的数据库操作提供了高层次的抽象。在本篇文章中,我们将介绍 SQLAlchemy 的两个主要组成部分:SQL 工具包 (SQL Toolkit) 和对象关系映射器 (Object-Relational Mapper, ORM) 的基本…...

微服务商城-商品微服务
数据表 CREATE TABLE product (id bigint(20) UNSIGNED NOT NULL AUTO_INCREMENT COMMENT 商品id,cateid smallint(6) UNSIGNED NOT NULL DEFAULT 0 COMMENT 类别Id,name varchar(100) NOT NULL DEFAULT COMMENT 商品名称,subtitle varchar(200) NOT NULL DEFAULT COMMENT 商…...

拉力测试cuda pytorch 把 4070显卡拉满
import torch import timedef stress_test_gpu(matrix_size16384, duration300):"""对GPU进行压力测试,通过持续的矩阵乘法来最大化GPU利用率参数:matrix_size: 矩阵维度大小,增大可提高计算复杂度duration: 测试持续时间(秒&…...

k8s业务程序联调工具-KtConnect
概述 原理 工具作用是建立了一个从本地到集群的单向VPN,根据VPN原理,打通两个内网必然需要借助一个公共中继节点,ktconnect工具巧妙的利用k8s原生的portforward能力,简化了建立连接的过程,apiserver间接起到了中继节…...

C++八股 —— 单例模式
文章目录 1. 基本概念2. 设计要点3. 实现方式4. 详解懒汉模式 1. 基本概念 线程安全(Thread Safety) 线程安全是指在多线程环境下,某个函数、类或代码片段能够被多个线程同时调用时,仍能保证数据的一致性和逻辑的正确性…...

[免费]微信小程序问卷调查系统(SpringBoot后端+Vue管理端)【论文+源码+SQL脚本】
大家好,我是java1234_小锋老师,看到一个不错的微信小程序问卷调查系统(SpringBoot后端Vue管理端)【论文源码SQL脚本】,分享下哈。 项目视频演示 【免费】微信小程序问卷调查系统(SpringBoot后端Vue管理端) Java毕业设计_哔哩哔哩_bilibili 项…...

实战三:开发网页端界面完成黑白视频转为彩色视频
一、需求描述 设计一个简单的视频上色应用,用户可以通过网页界面上传黑白视频,系统会自动将其转换为彩色视频。整个过程对用户来说非常简单直观,不需要了解技术细节。 效果图 二、实现思路 总体思路: 用户通过Gradio界面上…...

Pydantic + Function Calling的结合
1、Pydantic Pydantic 是一个 Python 库,用于数据验证和设置管理,通过 Python 类型注解强制执行数据类型。它广泛用于 API 开发(如 FastAPI)、配置管理和数据解析,核心功能包括: 数据验证:通过…...

客户案例 | 短视频点播企业海外视频加速与成本优化:MediaPackage+Cloudfront 技术重构实践
01技术背景与业务挑战 某短视频点播企业深耕国内用户市场,但其后台应用系统部署于东南亚印尼 IDC 机房。 随着业务规模扩大,传统架构已较难满足当前企业发展的需求,企业面临着三重挑战: ① 业务:国内用户访问海外服…...

【iOS】 Block再学习
iOS Block再学习 文章目录 iOS Block再学习前言Block的三种类型__ NSGlobalBlock____ NSMallocBlock____ NSStackBlock__小结 Block底层分析Block的结构捕获自由变量捕获全局(静态)变量捕获静态变量__block修饰符forwarding指针 Block的copy时机block作为函数返回值将block赋给…...

Mysql故障排插与环境优化
前置知识点 最上层是一些客户端和连接服务,包含本 sock 通信和大多数jiyukehuduan/服务端工具实现的TCP/IP通信。主要完成一些简介处理、授权认证、及相关的安全方案等。在该层上引入了线程池的概念,为通过安全认证接入的客户端提供线程。同样在该层上可…...
