基于weka手工实现K-means
一、K-means聚类算法
K均值聚类(K-means clustering)是一种常见的无监督学习算法,用于将数据集中的样本划分为K个不同的类别或簇。它通过最小化样本点与所属簇中心点之间的距离来确定最佳的簇划分。
K均值聚类的基本思想如下:
- 随机选择K个初始聚类中心(质心)。
- 对于每个样本,计算其与各个聚类中心之间的距离,并将样本分配到距离最近的聚类中心所代表的簇。
- 对于每个簇,计算簇中样本的均值,并将该均值作为新的聚类中心。
- 重复步骤2和步骤3,直到聚类中心不再变化或达到预定的迭代次数。
K均值聚类的关键是如何选择初始的聚类中心。常见的方法是随机选择数据集中的K个样本作为初始聚类中心,或者使用一些启发式的方法来选择。
K均值聚类的优点包括简单易实现、计算效率高和可扩展性好。它在许多领域中被广泛应用,如数据分析、图像处理、模式识别等。然而,K均值聚类也存在一些限制,例如对于初始聚类中心的敏感性、对于离群值的影响较大以及需要事先指定簇的个数K等。
在实际应用中,可以根据实际问题和数据集的特点来选择合适的K值,并进行多次运行以获得更稳定的结果。此外,K均值聚类也可以与其他算法相结合,如层次聚类(hierarchical clustering)和密度聚类(density-based clustering),以获得更好的聚类效果。
总的来说,K均值聚类是一种常用的无监督学习算法,用于将数据集中的样本划分为K个簇。它简单而高效,适用于许多聚类问题。然而,在使用K均值聚类时需要注意选择初始聚类中心和合适的K值,以及对其限制和局限性的认识。
二、基于weka手工实现K-means聚类算法
package weka.clusterers.myf;import weka.clusterers.RandomizableClusterer;
import weka.core.*;import java.util.*;/*** @author YFMan* @Description 自定义的 KMeans 聚类器* @Date 2023/6/8 15:01*/
public class myKMeans extends RandomizableClusterer {// 聚类中心的数量private int m_NumClusters = 2;// 不同聚类中心的集合private Instances m_ClusterCentroids;// 聚类的最大迭代次数private int m_MaxIterations = 500;// 追踪收敛前完成的迭代次数private int m_Iterations = 0;// 构造函数public myKMeans() {super();// 设置随机种子m_SeedDefault = 10;setSeed(m_SeedDefault);}/** @Author YFMan* @Description //基类定义的接口,必须要实现* @Date 2023/6/8 16:37* @Param []* @return weka.core.Capabilities**/@Overridepublic Capabilities getCapabilities() {Capabilities result = super.getCapabilities();result.disableAll();result.enable(Capabilities.Capability.NO_CLASS);// attributesresult.enable(Capabilities.Capability.NOMINAL_ATTRIBUTES);result.enable(Capabilities.Capability.NUMERIC_ATTRIBUTES);result.enable(Capabilities.Capability.MISSING_VALUES);return result;}/** @Author YFMan* @Description //进行聚类* @Date 2023/6/8 16:38* @Param [data 用于聚类的数据集]* @return void**/@Overridepublic void buildClusterer(Instances instances) throws Exception {// 迭代次数m_Iterations = 0;// 初始化聚类中心m_ClusterCentroids = new Instances(instances, m_NumClusters);// 每个样本属于哪个聚类中心int[] clusterAssignments = new int[instances.numInstances()];// 伪随机数生成器Random RandomO = new Random(getSeed());int instIndex;HashSet<Instance> initC = new HashSet<>();// 初始化聚类中心,随机选择 m_NumClusters 个样本作为聚类中心for (int j = instances.numInstances() - 1; j >= 0; j--) {instIndex = RandomO.nextInt(j + 1);if (!initC.contains(instances.instance(instIndex))) {m_ClusterCentroids.add(instances.instance(instIndex));initC.add(instances.instance(instIndex));}instances.swap(j, instIndex);if (m_ClusterCentroids.numInstances() == m_NumClusters) {break;}}boolean converged = false;// 用于存储每个聚类中心的样本集合Instances[] tempI = new Instances[m_NumClusters];while (!converged) {m_Iterations++;converged = true;// 计算每个样本 属于哪个聚类中心for (int i = 0; i < instances.numInstances(); i++) {Instance toCluster = instances.instance(i);int newC = clusterInstance(toCluster);// 如果样本所属的聚类中心发生变化,则说明还没有收敛if (newC != clusterAssignments[i]) {converged = false;}clusterAssignments[i] = newC;}// 重新计算聚类中心m_ClusterCentroids = new Instances(instances, m_NumClusters);for (int i = 0; i < m_NumClusters; i++) {tempI[i] = new Instances(instances, 0);}for (int i = 0; i < instances.numInstances(); i++) {tempI[clusterAssignments[i]].add(instances.instance(i));}// 重新计算聚类中心for (int i = 0; i < m_NumClusters; i++) {// 计算每个属性的平均值m_ClusterCentroids.add(calculateCentroid(tempI[i]));}// 如果迭代次数达到最大值,则强制结束if (m_Iterations == m_MaxIterations) {converged = true;}}}/** @Author YFMan* @Description //计算某个聚类中心的中心点* @Date 2023/6/8 16:57* @Param [instances 聚类中心的样本集合]* @return weka.core.Instance 聚类中心的中心点**/private Instance calculateCentroid(Instances instances) {int numInst = instances.numInstances();int numAttr = instances.numAttributes();Instance centroid = new Instance(numAttr);double sum;for (int i = 0; i < numAttr; i++) {sum = 0;for (int j = 0; j < numInst; j++) {sum += instances.instance(j).value(i);}centroid.setValue(i, sum / numInst);}return centroid;}/** @Author YFMan* @Description //计算两个属性全为数值类型的样本之间的距离(欧式距离)* @Date 2023/6/8 16:47* @Param [first 第一个样例, second 第二个样例]* @return double**/private double distance(Instance first, Instance second) {// 定义欧式距离double euclideanDistance = 0;// 定义overlapping距离double overlappingDistance = 0;for (int index = 0; index < first.numAttributes(); index++) {if (index == first.classIndex()) {continue;}// 如果是数值类型的属性,则计算欧式距离if (first.attribute(index).isNumeric()) {double dis = first.value(index) - second.value(index);euclideanDistance += dis * dis;} else {// 如果是标称类型的属性,则计算是否相等if (first.value(index) != second.value(index)) {overlappingDistance += 1;}}}return Math.sqrt(euclideanDistance) + overlappingDistance;}/** @Author YFMan* @Description //对一个给定的样例进行分类* @Date 2023/6/8 16:50* @Param [instance 给定的样例]* @return int 返回样例所属的聚类中心id**/@Overridepublic int clusterInstance(Instance instance) throws Exception {double minDist = Double.MAX_VALUE;int bestCluster = 0;for (int i = 0; i < m_NumClusters; i++) {double dist = distance(instance, m_ClusterCentroids.instance(i));if (dist < minDist) {minDist = dist;bestCluster = i;}}return bestCluster;}/** @Author YFMan* @Description //返回聚类中心的数量* @Date 2023/6/8 16:34* @Param []* @return int**/@Overridepublic int numberOfClusters() throws Exception {return m_NumClusters;}/** @Author YFMan* @Description //主函数* @Date 2023/6/8 16:33* @Param [argv 命令行参数]* @return void**/public static void main(String[] argv) {runClusterer(new myKMeans(), argv);}
}
相关文章:

基于weka手工实现K-means
一、K-means聚类算法 K均值聚类(K-means clustering)是一种常见的无监督学习算法,用于将数据集中的样本划分为K个不同的类别或簇。它通过最小化样本点与所属簇中心点之间的距离来确定最佳的簇划分。 K均值聚类的基本思想如下: …...
分布式系统监控zabbix安装部署及使用
分布式系统监控zabbix安装部署及使用 一.zabbix监控 1.什么是zabbix zabbix:是一款开源免费的,自动化发现服务与网络设备的分布式监控,可以监视应用层服务并以web前端页面集中管理并展示。 2.zabbix功能 监控服务器cpu负载、服务器内存使…...

【H5】使用 JavaScript 和 CSS 来完成实现鼠标接触时显示一个图片弹窗
以下是一个示例,演示了如何在鼠标接触时显示一个图片弹窗: HTML: <a href"#" class"popup-link" target"_blank"><i class"fab fa-weixin"></i> </a><div id"popup-containe…...

CSS选择器分类梳理并高亮重点
前言 主要内容来自菜鸟教程 CSS 选择器 | 菜鸟教程 分类是我自己理解的分类,示例说明优化统一了表述风格。 正文 选择器CSS示例示例说明基础*2*选择所有元素:root3:root选择文档的根元素element1p选择所有<p>元素:not(selector)3:not(p)选择所有并非p元素…...

Python批量给excel文件加密
有时候我们需要定期给公司外部发邮件,在自动化发邮件的时候需要对文件进行加密传输。本文和你一起来探索用python给单个文件和批量文件加密。 python自动化发邮件可参考【干货】用Python每天定时发送监控邮件。 文章目录 一、安装pypiwin32包二、定义给excel加…...

程序设计 树基础
✅作者简介:人工智能专业本科在读,喜欢计算机与编程,写博客记录自己的学习历程。 🍎个人主页:小嗷犬的个人主页 🍊个人网站:小嗷犬的技术小站 🥭个人信条:为天地立心&…...
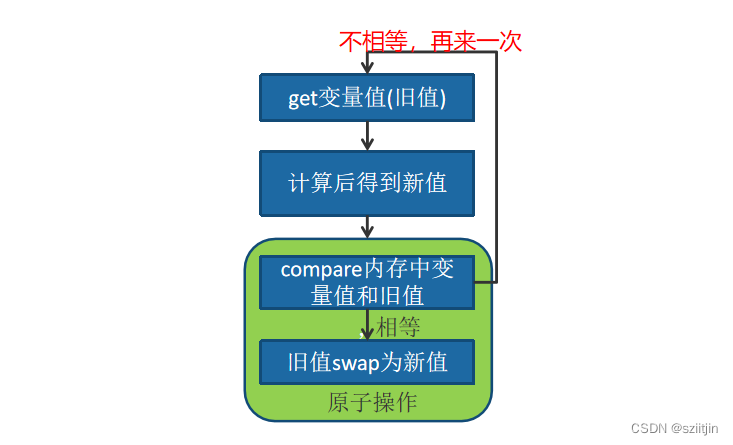
Java 并发编程与CAS基本原理
一、Java并发基础知识 Java里的程序天生就是多线程的,那么有几种新启线程的方式? 两种,启动线程的方式只有: 1、X extends Thread;,然后X.start; 2、X implements Runnable;然后交给Thread运行。 Java…...
qt creater运行按钮灰色,问题记录
第一次安装还没运行就出了三个错误: 1.F:\wei\Qt\Tools\CMake_64\share\cmake-3.24\Modules\CMakeTestCXXCompiler.cmake:62: error: The C compiler "C:/Program Files (x86)/Microsoft Visual Studio 14.0/VC/BIN/amd64/cl.exe" is not able to compil…...
【jvm】类加载器的分类
目录 一、说明二、示例2.1 代码2.2 截图 三、启动类加载器四、扩展类加载器五、应用程序类加载器 一、说明 1.jvm支持两种类型的类加载器,分别是引导类加载器(bootstrap classloader)和自定义类加载器(user-defined classloader&a…...
电路基础之电容
电容器(Capacitor)是由两个导体电极之间夹着一个电介质而组成的元件。这两个电极可以是金属板、箔片、涂层等,而电介质则是放置在电极之间的绝缘材料。电容器的基本构成包括以下几个要素: 电极:电容器的电极是两个导体…...

函数柯里化
文章目录 基本概念柯里化(Currying)是什么?通用的柯里化实现ES5 实现ES6 实现 基本概念 在讲柯里化之前我们先来了解一些基本概念: Function.length: length 属性指明函数的形参个数 function func1() {} function …...

【HBZ分享】ES中的Reindex重建索引
Reindex如何实现索引重建? 滚动索引 批量复制 Reindex存在的问题 如果新的索引没有提前创建好,并指定字段类型,那么重建后的新索引类型极有可能会和旧的索引不一致,因为ES他会推断类型,而推断错误率从实战来说那是…...

【PostgreSQL】几个提高性能的小特性
一、LOCALE 与 “operator class” 在PostgreSQL里,LOCALE默认使用C的本地化规则。LOCALE是一种文化偏好的区域设置,包括字母表、排序、数字格式等。 LOCALE里有一个比较重要的规则LC_COLLATE,即排序方式(Collation),它会对数据…...
[C语言] 指针
1. 指针是什么 2. 指针和指针类型 3. 野指针 4. 指针运算 5. 指针和数组 6. 二级指针 7. 指针数组 目录 1. 指针是什么? 2. 指针和指针类型 2.1 指针-整数 2.2 指针的解引用 3. 野指针 3.1 野指针成因 3.2 如何规避野指针 4. 指针运算 4.1 指针…...
win10在vmware15中安装macos10.13系统
第一步、安装vmware版本信息如下 第二步、下载unlocker-main和darwin.iso放到安装文件夹 第三步、管理员身份运行win-install.cmd 第四步、运行vmware新建虚拟机 第五步、启动新创建的虚拟机macOS 10.13并选择语言 第六步、选择磁盘工具抹掉磁盘 第七步、格式化完成后退出磁盘工…...

Node.js:实现遍历文件夹下所有文件
Node.js:实现遍历文件夹 代码如下 const fs require(fs) const path require(path)function traverseFolder(folderPath) {// 读取文件夹列表const files fs.readdirSync(folderPath)// 遍历文件夹列表files.forEach(function (fileName) {// 拼接当前文件路径…...
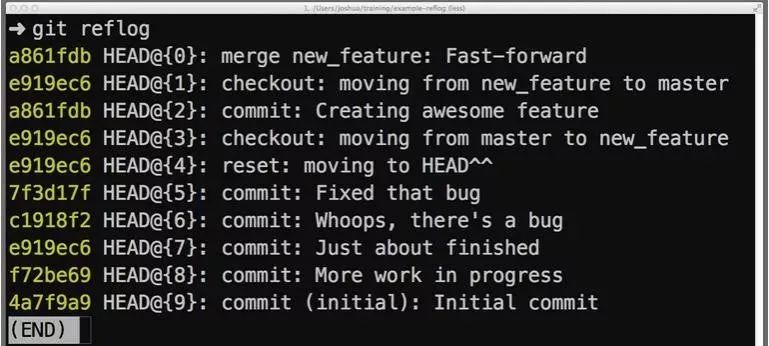
Git详解及使用
Git简介 Git 是一种分布式版本控制系统,它可以不受网络连接的限制,加上其它众多优点,目前已经成为程序开发人员做项目版本管理时的首选,非开发人员也可以用 Git 来做自己的文档版本管理工具。 大概是大二的时候开始接触和使用Gi…...
Jmeter设置中文的两种方式,建议使用第二种
方案一 进入jmeter图像化界面,选择Options下的Choose Language,再选择Chinese(Simplified)。这个就是选择语言为简体中文(缺陷:这个只是在本次使用时为中文,下次打开默认还是英文的) 方案二(…...

【ARM 嵌入式 编译系列 7.1 -- GCC 链接脚本中节区及各个段的详细介绍】
文章目录 什么是Section(节区)输入文件常见节区有哪些?什么是 glue code?.glue_7和.glue_7的作用是什么?链接脚本中的 KEEP 关键字是什么呢作用?链接脚本中的 PROVIDE 关键字是什么呢作用? 上篇文章:ARM 嵌…...

一文读懂HTML
文章目录 HTML的历史HTML的作用HTML的基本语言 HTML的历史 HTML(HyperText Markup Language)的历史可以追溯到20世纪90年代早期,它是互联网发展的重要里程碑之一。以下是HTML的历史概述: 早期阶段(1980年代末 - 1990年…...

python/java环境配置
环境变量放一起 python: 1.首先下载Python Python下载地址:Download Python | Python.org downloads ---windows -- 64 2.安装Python 下面两个,然后自定义,全选 可以把前4个选上 3.环境配置 1)搜高级系统设置 2…...

ESP32读取DHT11温湿度数据
芯片:ESP32 环境:Arduino 一、安装DHT11传感器库 红框的库,别安装错了 二、代码 注意,DATA口要连接在D15上 #include "DHT.h" // 包含DHT库#define DHTPIN 15 // 定义DHT11数据引脚连接到ESP32的GPIO15 #define D…...

微信小程序 - 手机震动
一、界面 <button type"primary" bindtap"shortVibrate">短震动</button> <button type"primary" bindtap"longVibrate">长震动</button> 二、js逻辑代码 注:文档 https://developers.weixin.qq…...

OkHttp 中实现断点续传 demo
在 OkHttp 中实现断点续传主要通过以下步骤完成,核心是利用 HTTP 协议的 Range 请求头指定下载范围: 实现原理 Range 请求头:向服务器请求文件的特定字节范围(如 Range: bytes1024-) 本地文件记录:保存已…...

RNN避坑指南:从数学推导到LSTM/GRU工业级部署实战流程
本文较长,建议点赞收藏,以免遗失。更多AI大模型应用开发学习视频及资料,尽在聚客AI学院。 本文全面剖析RNN核心原理,深入讲解梯度消失/爆炸问题,并通过LSTM/GRU结构实现解决方案,提供时间序列预测和文本生成…...

Device Mapper 机制
Device Mapper 机制详解 Device Mapper(简称 DM)是 Linux 内核中的一套通用块设备映射框架,为 LVM、加密磁盘、RAID 等提供底层支持。本文将详细介绍 Device Mapper 的原理、实现、内核配置、常用工具、操作测试流程,并配以详细的…...

ip子接口配置及删除
配置永久生效的子接口,2个IP 都可以登录你这一台服务器。重启不失效。 永久的 [应用] vi /etc/sysconfig/network-scripts/ifcfg-eth0修改文件内内容 TYPE"Ethernet" BOOTPROTO"none" NAME"eth0" DEVICE"eth0" ONBOOT&q…...
)
安卓基础(aar)
重新设置java21的环境,临时设置 $env:JAVA_HOME "D:\Android Studio\jbr" 查看当前环境变量 JAVA_HOME 的值 echo $env:JAVA_HOME 构建ARR文件 ./gradlew :private-lib:assembleRelease 目录是这样的: MyApp/ ├── app/ …...

HarmonyOS运动开发:如何用mpchart绘制运动配速图表
##鸿蒙核心技术##运动开发##Sensor Service Kit(传感器服务)# 前言 在运动类应用中,运动数据的可视化是提升用户体验的重要环节。通过直观的图表展示运动过程中的关键数据,如配速、距离、卡路里消耗等,用户可以更清晰…...

GO协程(Goroutine)问题总结
在使用Go语言来编写代码时,遇到的一些问题总结一下 [参考文档]:https://www.topgoer.com/%E5%B9%B6%E5%8F%91%E7%BC%96%E7%A8%8B/goroutine.html 1. main()函数默认的Goroutine 场景再现: 今天在看到这个教程的时候,在自己的电…...
