程序设计 树基础

✅作者简介:人工智能专业本科在读,喜欢计算机与编程,写博客记录自己的学习历程。
🍎个人主页:小嗷犬的个人主页
🍊个人网站:小嗷犬的技术小站
🥭个人信条:为天地立心,为生民立命,为往圣继绝学,为万世开太平。
本文目录
- 引入
- 定义
- 有关树的定义
- 适用于无根树和有根树
- 只适用于有根树
- 特殊的树
- 存储
- 只记录父结点
- 邻接表
- 左孩子右兄弟表示法
- 过程
- 实现
- 二叉树
- 树的遍历
- 树上 DFS
- 二叉树上 DFS
- 前序遍历
- 中序遍历
- 后序遍历
- 反推
- 树上 BFS
- 无根树
- 过程
- 实现
- 有根树
引入
图论中的树和现实生活中的树长得一样,只不过我们习惯于处理问题的时候把树根放到上方来考虑。
这种数据结构看起来像是一个倒挂的树,因此得名。
定义
一个没有固定根结点的树称为 无根树(unrooted tree)。无根树有几种等价的形式化定义:
- 有 n n n 个结点, n − 1 n-1 n−1 条边的连通无向图
- 无向无环的连通图
- 任意两个结点之间有且仅有一条简单路径的无向图
- 任何边均为桥的连通图
- 没有圈,且在任意不同两点间添加一条边之后所得图含唯一的一个圈的图
在无根树的基础上,指定一个结点称为 根,则形成一棵 有根树(rooted tree)。有根树在很多时候仍以无向图表示,只是规定了结点之间的上下级关系,详见下文。
有关树的定义
适用于无根树和有根树
- 森林(forest):每个连通分量(连通块)都是树的图。按照定义,一棵树也是森林。
- 生成树(spanning tree):一个连通无向图的生成子图,同时要求是树。也即在图的边集中选择 n − 1 n - 1 n−1 条,将所有顶点连通。
- 无根树的叶结点(leaf node):度数不超过 1 1 1 的结点。
- 有根树的叶结点(leaf node):没有子结点的结点。
只适用于有根树
-
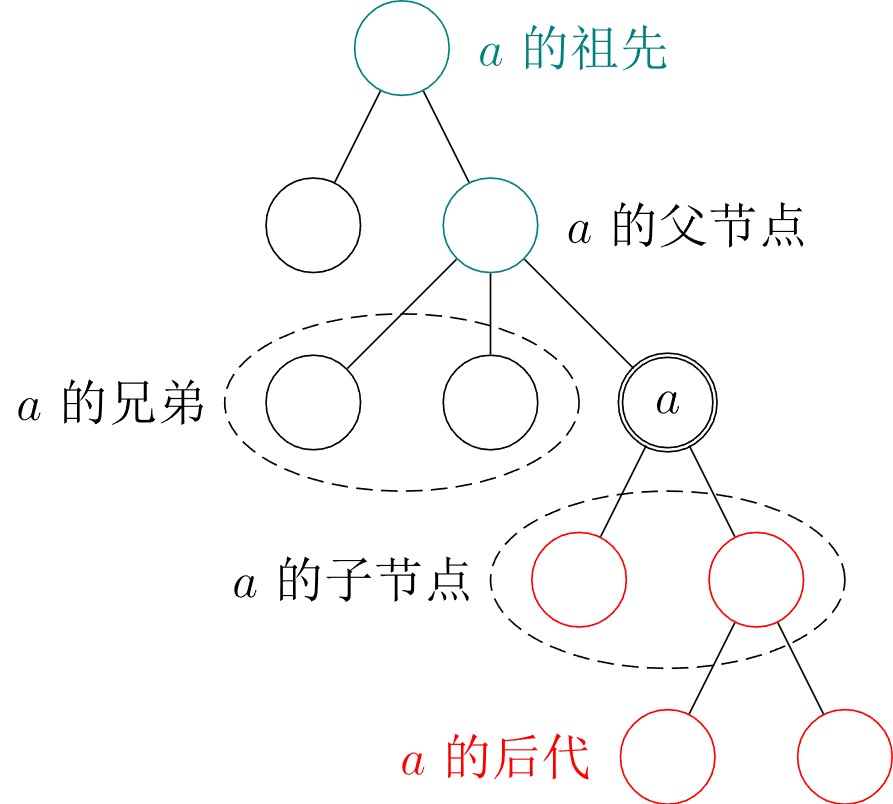
父亲(parent node):对于除根以外的每个结点,定义为从该结点到根路径上的第二个结点。 根结点没有父结点。
-
祖先(ancestor):一个结点到根结点的路径上,除了它本身外的结点。 根结点的祖先集合为空。
-
子结点(child node):如果 u u u 是 v v v 的父亲,那么 v v v 是 u u u 的子结点。
子结点的顺序一般不加以区分,二叉树是一个例外。 -
结点的深度(depth):到根结点的路径上的边数。
-
树的高度(height):所有结点的深度的最大值。
-
兄弟(sibling):同一个父亲的多个子结点互为兄弟。
-
后代(descendant):子结点和子结点的后代。
或者理解成:如果 u u u 是 v v v 的祖先,那么 v v v 是 u u u 的后代。
-
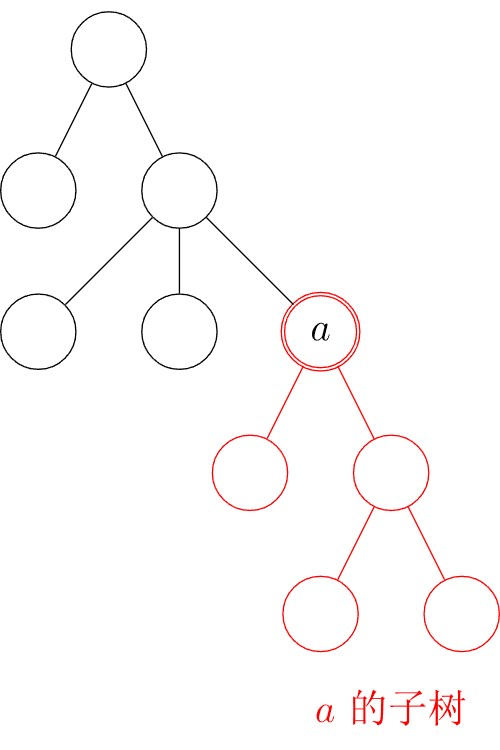
子树(subtree):删掉与父亲相连的边后,该结点所在的子图。
特殊的树
-
链(chain/path graph):满足与任一结点相连的边不超过 2 2 2 条的树称为链。
-
菊花/星星(star):满足存在 u u u 使得所有除 u u u 以外结点均与 u u u 相连的树称为菊花。
-
有根二叉树(rooted binary tree):每个结点最多只有两个儿子(子结点)的有根树称为二叉树。常常对两个子结点的顺序加以区分,分别称之为左子结点和右子结点。
大多数情况下,二叉树 一词均指有根二叉树。 -
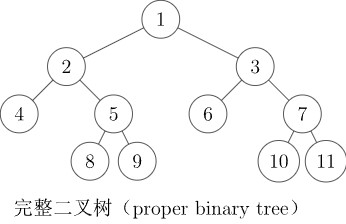
完整二叉树(full/proper binary tree):每个结点的子结点数量均为 0 0 0 或者 2 2 2 的二叉树。换言之,每个结点或者是树叶,或者左右子树均非空。
-
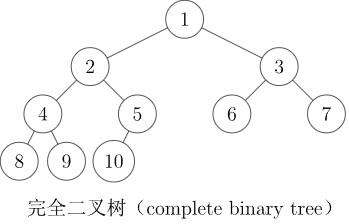
完全二叉树(complete binary tree):只有最下面两层结点的度数可以小于 2 2 2,且最下面一层的结点都集中在该层最左边的连续位置上。
-
完美二叉树(perfect binary tree):所有叶结点的深度均相同的二叉树称为完美二叉树。
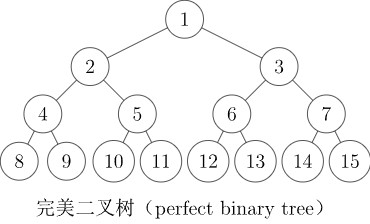
Proper binary tree 的汉译名称不固定,且完全二叉树和满二叉树的定义在不同教材中定义不同,遇到的时候需根据上下文加以判断。
ACMer 所说的「满二叉树」多指完美二叉树。
存储
只记录父结点
用一个数组 parent[N] 记录每个结点的父亲结点。
这种方式可以获得的信息较少,不便于进行自顶向下的遍历。常用于自底向上的递推问题中。
邻接表
-
对于无根树:为每个结点开辟一个线性列表,记录所有与之相连的结点。
std::vector<int> adj[N]; -
对于有根树:
-
方法一:若给定的是无向图,则仍可以上述形式存储。下文将介绍如何区分结点的上下关系。
-
方法二:若输入数据能够确保结点的上下关系,则可以利用这个信息。为每个结点开辟一个线性列表,记录其所有子结点;若有需要,还可在另一个数组中记录其父结点。
std::vector<int> children[N]; int parent[N];当然也可以用其他方式(如链表)替代
std::vector。
-
左孩子右兄弟表示法
过程
对于有根树,存在一种简单的表示方法。
首先,给每个结点的所有子结点任意确定一个顺序。
此后为每个结点记录两个值:其 第一个子结点 child[u] 和其 下一个兄弟结点 sib[u]。若没有子结点,则 child[u] 为空;若该结点是其父结点的最后一个子结点,则 sib[u] 为空。
实现
遍历一个结点的所有子结点可由如下方式实现。
int v = child[u]; // 从第一个子结点开始
while (v != EMPTY_NODE)
{// ...// 处理子结点 v// ...v = sib[v]; // 转至下一个子结点,即 v 的一个兄弟
}
也可简写为以下形式。
for (int v = child[u]; v != EMPTY_NODE; v = sib[v])
{// ...// 处理子结点 v// ...
}
二叉树
需要记录每个结点的左右子结点。
int parent[N];
int lch[N], rch[N];
// -- or --
int child[N][2];
树的遍历
树上 DFS
在树上 DFS 是这样的一个过程:先访问根节点,然后分别访问根节点每个儿子的子树。
可以用来求出每个节点的深度、父亲等信息。
二叉树上 DFS
前序遍历
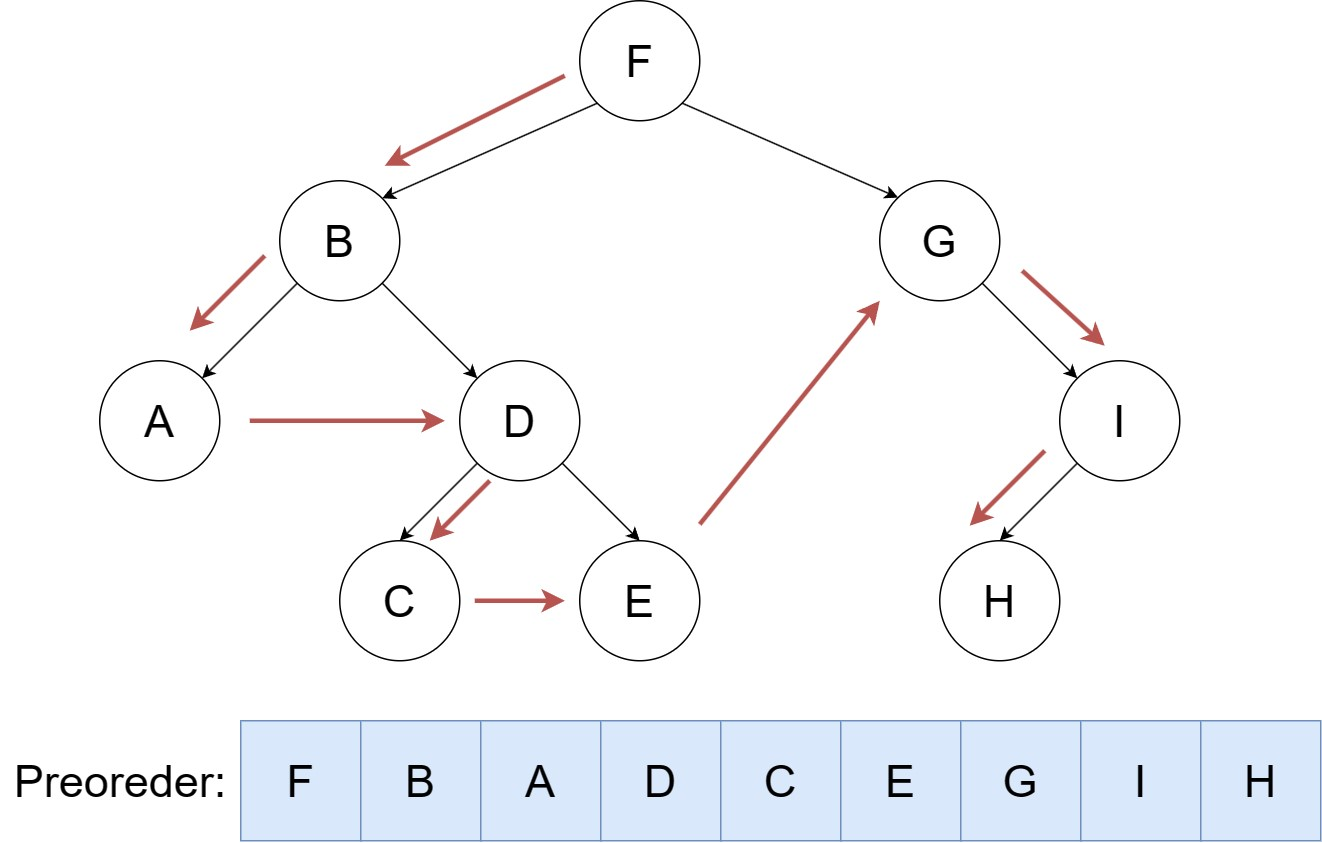
按照 根,左,右 的顺序遍历二叉树。
void preTrav(BiTree *root)
{if (root){cout << root->key << " ";preTrav(root->left);preTrav(root->right);}
}
中序遍历
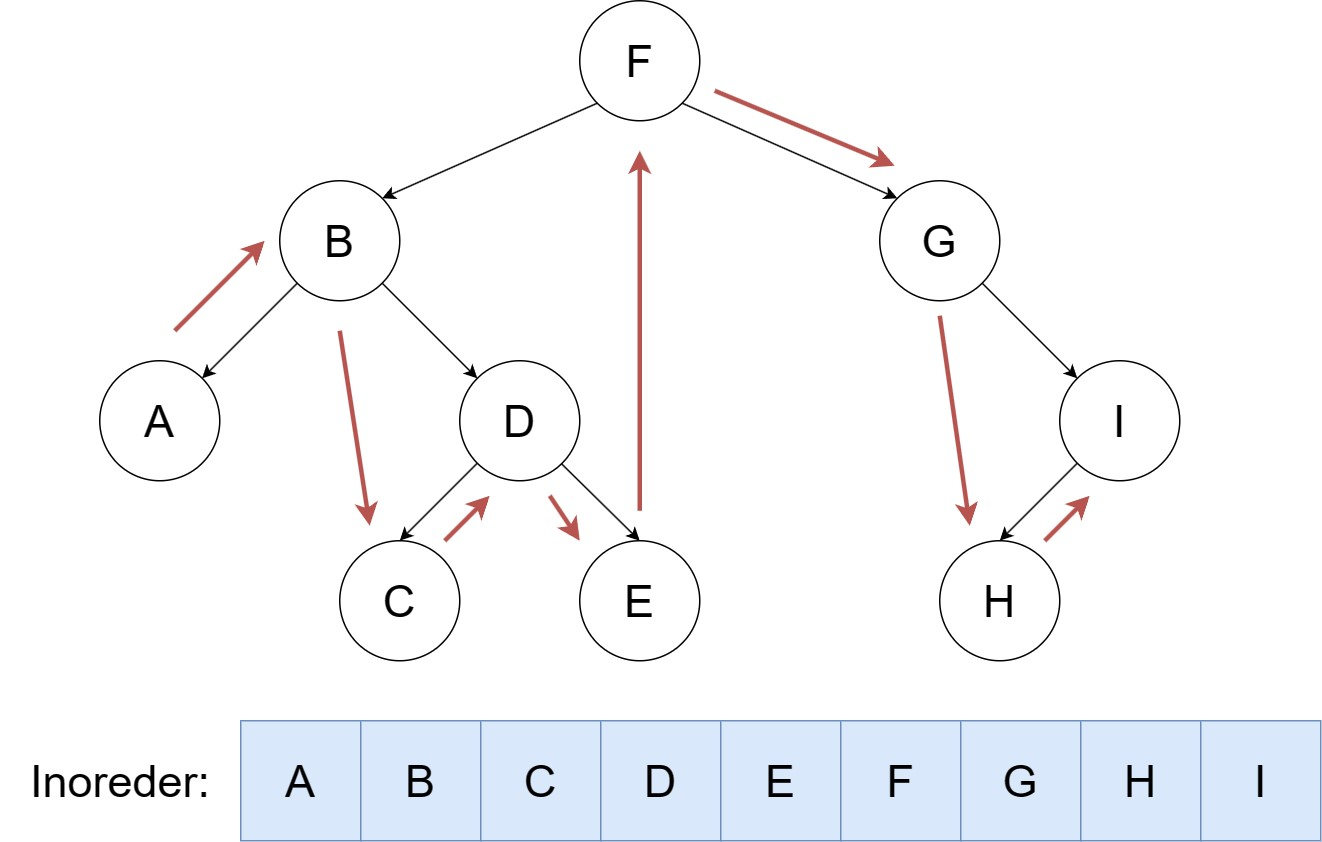
按照 左,根,右 的顺序遍历二叉树。
void midTrav(BiTree *root)
{if (root){midTrav(root->left);cout << root->key << " ";midTrav(root->right);}
}
后序遍历
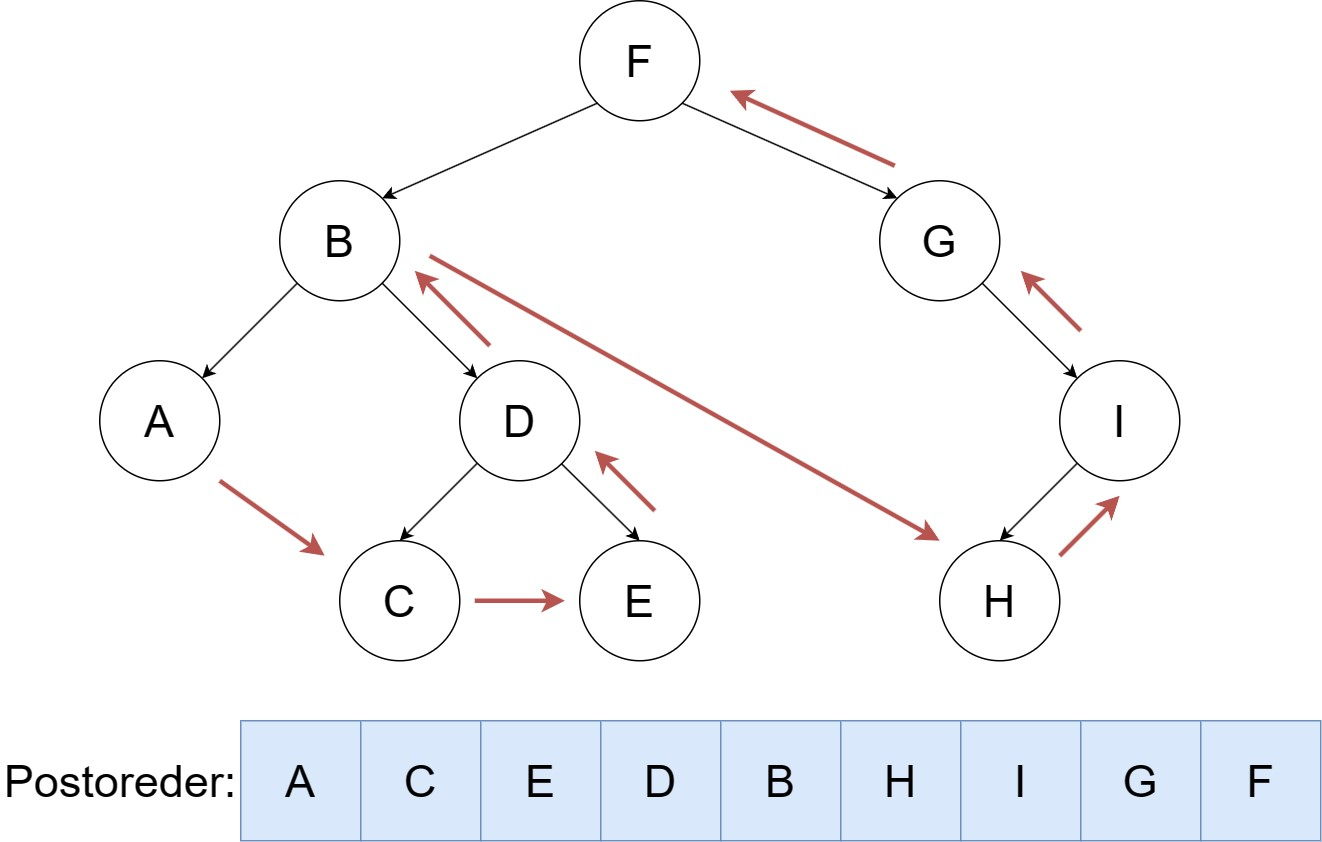
按照 左,右,根 的顺序遍历二叉树。
void lastTrav(BiTree *root)
{if (root){lastTrav(root->left);lastTrav(root->right);cout << root->key << " ";}
}
反推
已知中序遍历序列和另外一个序列可以求第三个序列。

- 前序的第一个是 root,后序的最后一个是 root。
- 先确定根节点,然后根据中序遍历,在根左边的为左子树,根右边的为右子树。
- 对于每一个子树可以看成一个全新的树,仍然遵循上面的规律。
树上 BFS
从树根开始,严格按照层次来访问节点。
BFS 过程中也可以顺便求出各个节点的深度和父亲节点。
无根树
过程
树的遍历一般为深度优先遍历,这个过程中最需要注意的是避免重复访问结点。
由于树是无环图,因此只需记录当前结点是由哪个结点访问而来,此后进入除该结点外的所有相邻结点,即可避免重复访问。
实现
void dfs(int u, int from)
{// 递归进入除了 from 之外的所有子结点// 对于出发结点,from 为空,故会访问所有相邻结点,这与期望一致for (int v : adj[u])if (v != from)dfs(v, u);
}// 开始遍历时
int EMPTY_NODE = -1; // 一个不存在的编号
int root = 0; // 任取一个结点作为出发点
dfs(root, EMPTY_NODE);
有根树
对于有根树,需要区分结点的上下关系。
考察上面的遍历过程,若从根开始遍历,则访问到一个结点时 from 的值,就是其父结点的编号。
通过这个方式,可以对于无向的输入求出所有结点的父结点,以及子结点列表。
相关文章:

程序设计 树基础
✅作者简介:人工智能专业本科在读,喜欢计算机与编程,写博客记录自己的学习历程。 🍎个人主页:小嗷犬的个人主页 🍊个人网站:小嗷犬的技术小站 🥭个人信条:为天地立心&…...
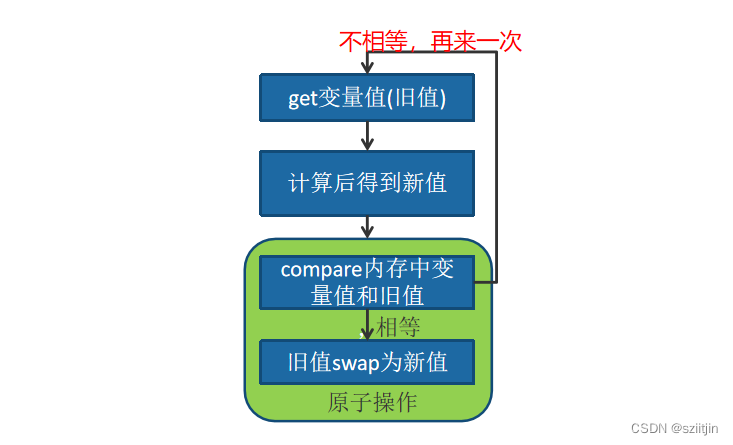
Java 并发编程与CAS基本原理
一、Java并发基础知识 Java里的程序天生就是多线程的,那么有几种新启线程的方式? 两种,启动线程的方式只有: 1、X extends Thread;,然后X.start; 2、X implements Runnable;然后交给Thread运行。 Java…...
qt creater运行按钮灰色,问题记录
第一次安装还没运行就出了三个错误: 1.F:\wei\Qt\Tools\CMake_64\share\cmake-3.24\Modules\CMakeTestCXXCompiler.cmake:62: error: The C compiler "C:/Program Files (x86)/Microsoft Visual Studio 14.0/VC/BIN/amd64/cl.exe" is not able to compil…...
【jvm】类加载器的分类
目录 一、说明二、示例2.1 代码2.2 截图 三、启动类加载器四、扩展类加载器五、应用程序类加载器 一、说明 1.jvm支持两种类型的类加载器,分别是引导类加载器(bootstrap classloader)和自定义类加载器(user-defined classloader&a…...
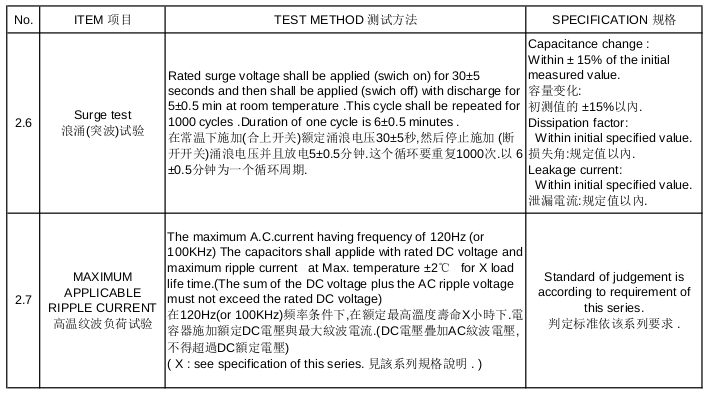
电路基础之电容
电容器(Capacitor)是由两个导体电极之间夹着一个电介质而组成的元件。这两个电极可以是金属板、箔片、涂层等,而电介质则是放置在电极之间的绝缘材料。电容器的基本构成包括以下几个要素: 电极:电容器的电极是两个导体…...

函数柯里化
文章目录 基本概念柯里化(Currying)是什么?通用的柯里化实现ES5 实现ES6 实现 基本概念 在讲柯里化之前我们先来了解一些基本概念: Function.length: length 属性指明函数的形参个数 function func1() {} function …...

【HBZ分享】ES中的Reindex重建索引
Reindex如何实现索引重建? 滚动索引 批量复制 Reindex存在的问题 如果新的索引没有提前创建好,并指定字段类型,那么重建后的新索引类型极有可能会和旧的索引不一致,因为ES他会推断类型,而推断错误率从实战来说那是…...

【PostgreSQL】几个提高性能的小特性
一、LOCALE 与 “operator class” 在PostgreSQL里,LOCALE默认使用C的本地化规则。LOCALE是一种文化偏好的区域设置,包括字母表、排序、数字格式等。 LOCALE里有一个比较重要的规则LC_COLLATE,即排序方式(Collation),它会对数据…...
[C语言] 指针
1. 指针是什么 2. 指针和指针类型 3. 野指针 4. 指针运算 5. 指针和数组 6. 二级指针 7. 指针数组 目录 1. 指针是什么? 2. 指针和指针类型 2.1 指针-整数 2.2 指针的解引用 3. 野指针 3.1 野指针成因 3.2 如何规避野指针 4. 指针运算 4.1 指针…...
win10在vmware15中安装macos10.13系统
第一步、安装vmware版本信息如下 第二步、下载unlocker-main和darwin.iso放到安装文件夹 第三步、管理员身份运行win-install.cmd 第四步、运行vmware新建虚拟机 第五步、启动新创建的虚拟机macOS 10.13并选择语言 第六步、选择磁盘工具抹掉磁盘 第七步、格式化完成后退出磁盘工…...

Node.js:实现遍历文件夹下所有文件
Node.js:实现遍历文件夹 代码如下 const fs require(fs) const path require(path)function traverseFolder(folderPath) {// 读取文件夹列表const files fs.readdirSync(folderPath)// 遍历文件夹列表files.forEach(function (fileName) {// 拼接当前文件路径…...
Git详解及使用
Git简介 Git 是一种分布式版本控制系统,它可以不受网络连接的限制,加上其它众多优点,目前已经成为程序开发人员做项目版本管理时的首选,非开发人员也可以用 Git 来做自己的文档版本管理工具。 大概是大二的时候开始接触和使用Gi…...
Jmeter设置中文的两种方式,建议使用第二种
方案一 进入jmeter图像化界面,选择Options下的Choose Language,再选择Chinese(Simplified)。这个就是选择语言为简体中文(缺陷:这个只是在本次使用时为中文,下次打开默认还是英文的) 方案二(…...

【ARM 嵌入式 编译系列 7.1 -- GCC 链接脚本中节区及各个段的详细介绍】
文章目录 什么是Section(节区)输入文件常见节区有哪些?什么是 glue code?.glue_7和.glue_7的作用是什么?链接脚本中的 KEEP 关键字是什么呢作用?链接脚本中的 PROVIDE 关键字是什么呢作用? 上篇文章:ARM 嵌…...

一文读懂HTML
文章目录 HTML的历史HTML的作用HTML的基本语言 HTML的历史 HTML(HyperText Markup Language)的历史可以追溯到20世纪90年代早期,它是互联网发展的重要里程碑之一。以下是HTML的历史概述: 早期阶段(1980年代末 - 1990年…...
MOCK测试
介绍 mock:就是对于一些难以构造的对象,使用虚拟的技术来实现测试的过程。 mock测试:在测试过程中,对于某些不容易构造或者不容易获取的对象,可以用一个虚拟的对象来代替的测试方 法。 接口Mock测试:在接口…...
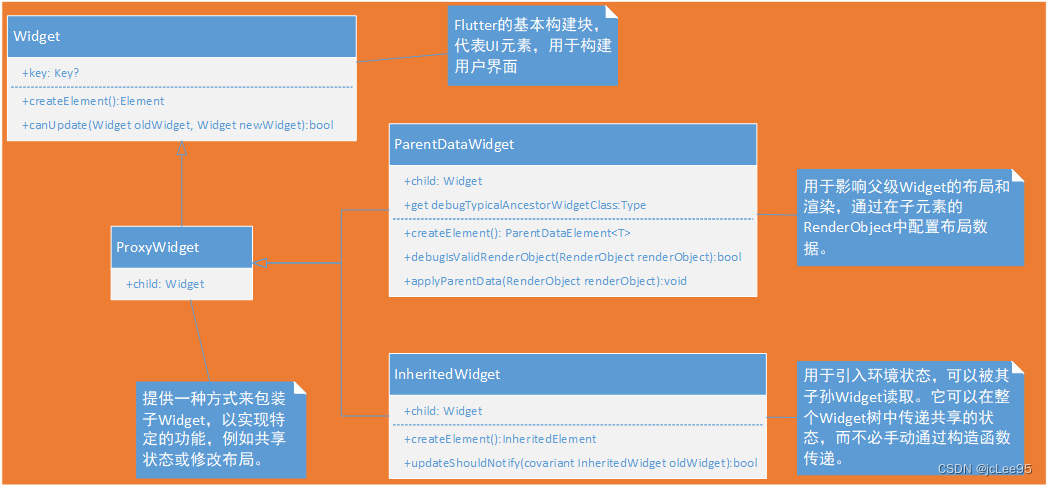
Flutter源码分析笔记:Widget类源码分析
Flutter源码分析笔记 Widget类源码分析 - 文章信息 - Author: 李俊才 (jcLee95) Visit me at: https://jclee95.blog.csdn.netEmail: 291148484163.com. Shenzhen ChinaAddress of this article:https://blog.csdn.net/qq_28550263/article/details/132259681 【介绍】&#x…...

PyTorch 微调终极指南:第 2 部分 — 提高模型准确性
一、说明 如今,在训练深度学习模型时,通过在自己的数据上微调预训练模型来迁移学习已成为首选方法。通过微调这些模型,我们可以利用他们的专业知识并使其适应我们的特定任务,从而节省宝贵的时间和计算资源。本文分为四个部分&…...
MySQL数据库----------安装anaconda---------python与数据库的链接
作者前言 🎂 ✨✨✨✨✨✨🍧🍧🍧🍧🍧🍧🍧🎂 🎂 作者介绍: 🎂🎂 🎂 🎉🎉🎉…...

nuxt页面布局
nuxt页面默认布局文件在layouts目录下default.vue,可将页面的头部和脚部提取出来,形成布局页,将主内容区域的内容替换成<nuxt />。附default.vue代码: <template><div class"app-container"><div…...

Python:操作 Excel 折叠
💖亲爱的技术爱好者们,热烈欢迎来到 Kant2048 的博客!我是 Thomas Kant,很开心能在CSDN上与你们相遇~💖 本博客的精华专栏: 【自动化测试】 【测试经验】 【人工智能】 【Python】 Python 操作 Excel 系列 读取单元格数据按行写入设置行高和列宽自动调整行高和列宽水平…...

3.3.1_1 检错编码(奇偶校验码)
从这节课开始,我们会探讨数据链路层的差错控制功能,差错控制功能的主要目标是要发现并且解决一个帧内部的位错误,我们需要使用特殊的编码技术去发现帧内部的位错误,当我们发现位错误之后,通常来说有两种解决方案。第一…...

可靠性+灵活性:电力载波技术在楼宇自控中的核心价值
可靠性灵活性:电力载波技术在楼宇自控中的核心价值 在智能楼宇的自动化控制中,电力载波技术(PLC)凭借其独特的优势,正成为构建高效、稳定、灵活系统的核心解决方案。它利用现有电力线路传输数据,无需额外布…...

工程地质软件市场:发展现状、趋势与策略建议
一、引言 在工程建设领域,准确把握地质条件是确保项目顺利推进和安全运营的关键。工程地质软件作为处理、分析、模拟和展示工程地质数据的重要工具,正发挥着日益重要的作用。它凭借强大的数据处理能力、三维建模功能、空间分析工具和可视化展示手段&…...

第25节 Node.js 断言测试
Node.js的assert模块主要用于编写程序的单元测试时使用,通过断言可以提早发现和排查出错误。 稳定性: 5 - 锁定 这个模块可用于应用的单元测试,通过 require(assert) 可以使用这个模块。 assert.fail(actual, expected, message, operator) 使用参数…...

SpringCloudGateway 自定义局部过滤器
场景: 将所有请求转化为同一路径请求(方便穿网配置)在请求头内标识原来路径,然后在将请求分发给不同服务 AllToOneGatewayFilterFactory import lombok.Getter; import lombok.Setter; import lombok.extern.slf4j.Slf4j; impor…...

vue3+vite项目中使用.env文件环境变量方法
vue3vite项目中使用.env文件环境变量方法 .env文件作用命名规则常用的配置项示例使用方法注意事项在vite.config.js文件中读取环境变量方法 .env文件作用 .env 文件用于定义环境变量,这些变量可以在项目中通过 import.meta.env 进行访问。Vite 会自动加载这些环境变…...

Maven 概述、安装、配置、仓库、私服详解
目录 1、Maven 概述 1.1 Maven 的定义 1.2 Maven 解决的问题 1.3 Maven 的核心特性与优势 2、Maven 安装 2.1 下载 Maven 2.2 安装配置 Maven 2.3 测试安装 2.4 修改 Maven 本地仓库的默认路径 3、Maven 配置 3.1 配置本地仓库 3.2 配置 JDK 3.3 IDEA 配置本地 Ma…...

鸿蒙DevEco Studio HarmonyOS 5跑酷小游戏实现指南
1. 项目概述 本跑酷小游戏基于鸿蒙HarmonyOS 5开发,使用DevEco Studio作为开发工具,采用Java语言实现,包含角色控制、障碍物生成和分数计算系统。 2. 项目结构 /src/main/java/com/example/runner/├── MainAbilitySlice.java // 主界…...

代码随想录刷题day30
1、零钱兑换II 给你一个整数数组 coins 表示不同面额的硬币,另给一个整数 amount 表示总金额。 请你计算并返回可以凑成总金额的硬币组合数。如果任何硬币组合都无法凑出总金额,返回 0 。 假设每一种面额的硬币有无限个。 题目数据保证结果符合 32 位带…...
