算法练习Day43|● 518. 零钱兑换 II ● 377. 组合总和 Ⅳ
LeetCode:518. 零钱兑换 II
518. 零钱兑换 II - 力扣(LeetCode)
1.思路
求组合数,先遍历物品再遍历背包,dp[]数组累加即可。
2.代码实现
1class Solution {2 public int change(int amount, int[] coins) {34 int[] dp = new int[amount + 1];5 dp[0] = 1;67 for (int i = 0; i < coins.length; i++) {8 for (int j = coins[i]; j <= amount; j++) {9 dp[j] += dp[j - coins[i]];
10 }
11 }
12 return dp[amount];
13 }
14}
3.复杂度分析
时间复杂度:O(nm). 空间复杂度:O(nm).
LeetCode:377. 组合总和 Ⅳ
377. 组合总和 Ⅳ - 力扣(LeetCode)
1.思路
声明初始化dp数组,求排列,先遍历背包后遍历物品。dp[]数组累加操作。
2.代码实现
1class Solution {2 public int combinationSum4(int[] nums, int target) {3 int[] dp = new int[target + 1];4 dp[0] = 1;56 for (int i = 0; i <= target; i++) {7 for (int j = 0; j < nums.length; j++) {8 if (i >= nums[j]) {9 dp[i] += dp[i - nums[j]];
10 }
11 }
12 }
13 return dp[target];
14 }
15}
3.复杂度分析
时间复杂度:O(nm). 空间复杂度:O(nm).
相关文章:

算法练习Day43|● 518. 零钱兑换 II ● 377. 组合总和 Ⅳ
LeetCode:518. 零钱兑换 II 518. 零钱兑换 II - 力扣(LeetCode) 1.思路 求组合数,先遍历物品再遍历背包,dp[]数组累加即可。 2.代码实现 1class Solution {2 public int change(int amount, int[] coins) {34 int[…...
人类:我觉得1+1=956446,你觉得呢?大模型:啊对对对
大模型太「听话」了怎么办? 大型语言模型(LLM)的自然语言理解与生成能力一直备受称赞,特别是 ChatGPT 等对话式语言模型能够与人类流畅、自然地进行多轮对话。然而,最近一篇 Google DeepMind 的论文研究发现 LLM 普遍存…...
Offset Explorer
Offset Explorer 简介下载安装 简介 Offset Explorer(以前称为Kafka Tool)是一个用于管理和使Apache Kafka 集群的GUI应用程序。它提供了一个直观的UI,允许人们快速查看Kafka集群中的对象以及存储在集群主题中的消息。它包含面向开发人员和管…...

查看CentOS版本及系统位数与设置CentOS 7.9 2009 防火墙配置放开端口的命令与过程
一、查看CentOS版本及系统位数 1.1 命令汇总 //1、安装redhat-lsb yum install -y redhat-lsb//2、查看系统版本信息 lsb_release -a //3、查看系统位数 getconf LONG_BIT1.2 截图 二、设置CentOS7.9 2009 防火墙配置放开端口 2.1 命令汇总 //禁止防火墙开机启动。这种方法方…...

前端css高级
day08-CSS高级 目标:掌握定位的作用及特点;掌握 CSS 高级技巧 01-定位 作用:灵活的改变盒子在网页中的位置 实现: 1.定位模式:position 2.边偏移:设置盒子的位置 leftrighttopbottom 相对定位 posit…...

华为OD真题--字符串中最小的整数和--带答案
1. 华为OD机考题 答案 2023华为OD统一考试(AB卷)题库清单-带答案(持续更新) 2023年华为OD真题机考题库大全-带答案(持续更新) 2. 面试题 一手真实java面试题:2023年各大公司java面试真题汇总--…...
9月30日生效:微软官方服务协议更新,防止人工智能进行逆向工程
微软最近更新了其官方服务协议,新规则将于9月30日生效,包括多个新增和变化,具体细节请参考最新的微软服务协议。 微软最新更新涉及使用Bing Chat聊天机器人、Windows Copilot和Microsoft 365 Copilot服务,引起了广泛关注。这次更新…...
80分就合格)
HarmonyOS教育类APP项目实战系列课结课考试答案(1-10讲)80分就合格
王丹辉(第一讲):HarmonyOS教育类APP项目实战开课及低代码初体验 结课考试 及格分80/ 满分100 评价 判断题 1. DevEco Studio不能同时支持HarmonyOS和OpenHarmony应用/服务开发 正确(True)错误(False) 回答正确 2. DevEco Studio…...

为什么要学习Oracle技术?
为什么要学习Oracle技术? 众所周知,Oracle占据着企业数据库领域超过48.1%的市场份额,成为高端企业数据库软件的绝对领导者。随着时间的推移,企业数据库的规模不断扩大,富有经验的资深OracleDBA越来越受到企业的欢迎。我们从著名的…...

ffmpeg+intel核显实现硬解码
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 前言一、前言二、检查方法1.图形法2.nvidia-smi3.intel-gpu-tools 三、安装使用1.libva-dev2.libva-utils3.编译安装4.测试1.vainfo2.ffmpeg测试解码 总结 前言 之…...
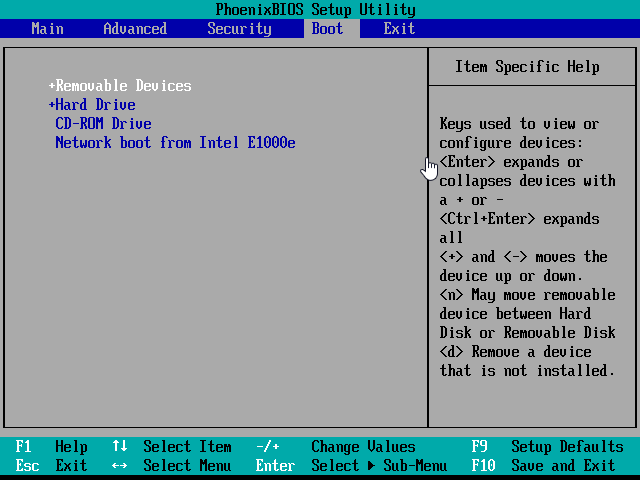
电脑开机出现Boot Device怎么办?
开机出现Boot Device这个问题很常见,有时还会出现No Boot Device的问题,虽然多了一个单词,但意思是相同的,这些问题说明你的系统盘出现了问题,或者是引导出现了问题。这该如何解决呢? 方法1. 检查主板或硬盘…...

面试题. 一次编辑
字符串有三种编辑操作:插入一个英文字符、删除一个英文字符或者替换一个英文字符。 给定两个字符串,编写一个函数判定它们是否只需要一次(或者零次)编辑。 示例 1: 输入: first "pale" second "ple" 输出: True 示例 2: 输入: first &…...

Unity悬浮显示提示内容
在编写unity时,需要实现鼠标在某一个按钮上时,就显示其子物体中对应的下拉菜单,为此编写了一个公共类,对于需要悬浮显示的控件均可挂载此类。代码如下: using UnityEngine; using UnityEngine.EventSystems; using Un…...

变形金刚在图像识别方面比CNN更好吗?
链接到文 — https://arxiv.org/pdf/2010.11929.pdf 一、说明 如今,在自然语言处理(NLP)任务中,转换器已成为goto架构(例如BERT,GPT-3等)。另一方面,变压器在计算机视觉任务中的使用…...

【Javascript】ES6新增之类的认识
在现代编程语言中,类是面向对象编程范式中的核心概念之一。 与函数类似,类本质上是一种特殊的函数,它允许我们将数据和操作封装在一起,以创建具有共同行为和状态的对象。 在类的世界里,我们有类表达式和类声明…...

C#随机法 双峰函数 求极值 避免落入局部最优解
避免落入局部最优解,只要让步长够长即可。 x1 resultX1 random1.NextDouble()*100; 如果后面不乘以100,则很大概率落入负数的最大值 Random random1 new Random(DateTime.Now.Millisecond);double x1 0, resultX10,max-999999,maxTemp0;for (int i …...

JavaScript高级:常见设计模式
设计模式是在软件开发中重复出现的问题的解决方案,它们是经过验证的、被广泛接受的最佳实践。设计模式可以让我们避免重复造轮子,提高代码质量和可维护性。在本文中,我们将介绍几种常见的设计模式,以及它们的实现和应用。 1. 单例…...

32bit国产低功耗无线MCU芯片
超低功耗无线MCU芯片MS1642,集成了高性能的32位ARMCortex-M0内核,宽电压工作范围的MCU。嵌入高达64Kbytes高可靠Flash和8Kbytes SRAM存储器,最高工作频率32MHz。芯片集成多路I2C、USART等通讯外设,1路12bit ADC,5个16b…...
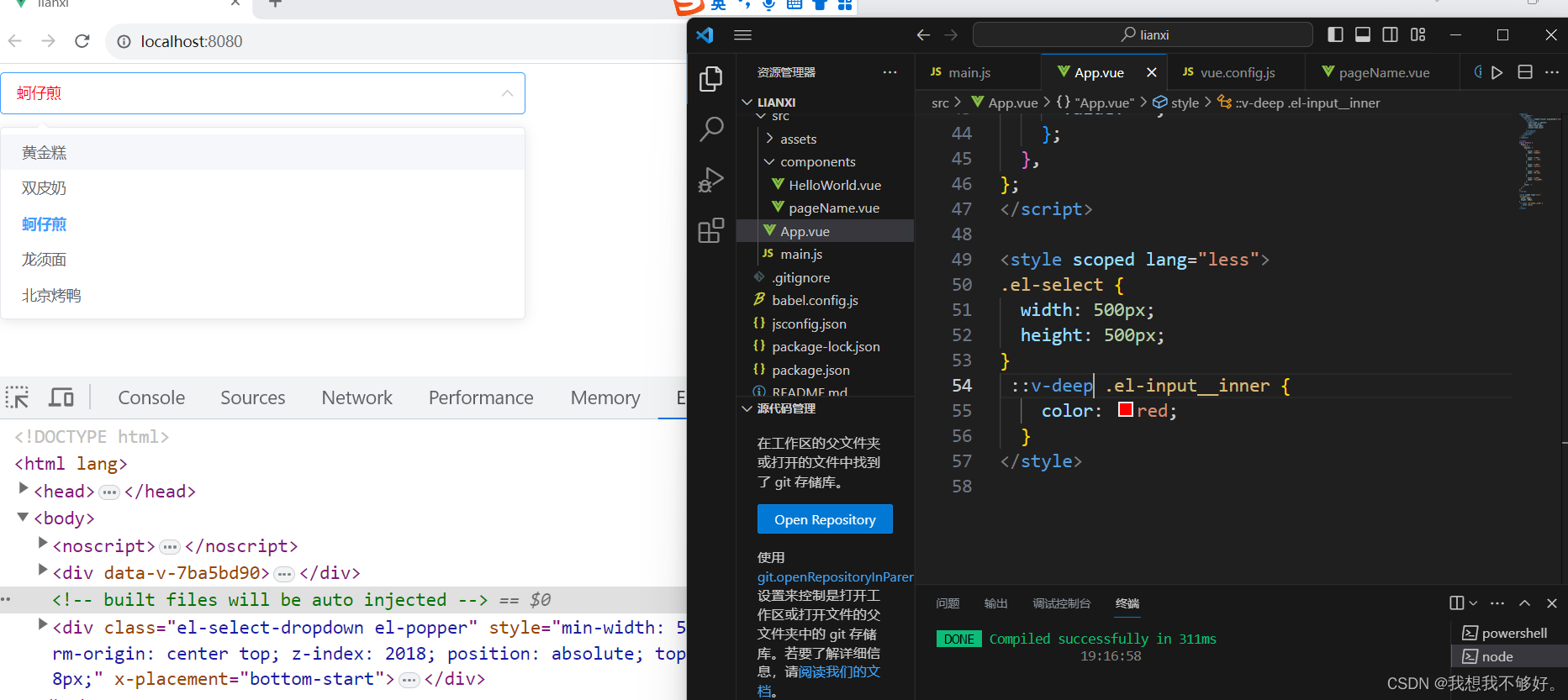
scope组件穿透
今天我们以单选框为例来探究一下样式的穿透问题 1.代码 <template><div class""><el-radio v-model"radio" label"1">备选项</el-radio><el-radio v-model"radio" label"2">备选项</el-r…...

分类预测 | Python实现LR逻辑回归多输入分类预测
分类预测 | Python实现LR逻辑回归多输入分类预测 目录 分类预测 | Python实现LR逻辑回归多输入分类预测基本介绍模型描述源码设计学习小结参考资料基本介绍 逻辑回归是一种广义线性的分类模型且其模型结构可以视为单层的神经网络,由一层输入层、一层仅带有一个sigmoid激活函数…...

MPNet:旋转机械轻量化故障诊断模型详解python代码复现
目录 一、问题背景与挑战 二、MPNet核心架构 2.1 多分支特征融合模块(MBFM) 2.2 残差注意力金字塔模块(RAPM) 2.2.1 空间金字塔注意力(SPA) 2.2.2 金字塔残差块(PRBlock) 2.3 分类器设计 三、关键技术突破 3.1 多尺度特征融合 3.2 轻量化设计策略 3.3 抗噪声…...

【Linux】shell脚本忽略错误继续执行
在 shell 脚本中,可以使用 set -e 命令来设置脚本在遇到错误时退出执行。如果你希望脚本忽略错误并继续执行,可以在脚本开头添加 set e 命令来取消该设置。 举例1 #!/bin/bash# 取消 set -e 的设置 set e# 执行命令,并忽略错误 rm somefile…...

ES6从入门到精通:前言
ES6简介 ES6(ECMAScript 2015)是JavaScript语言的重大更新,引入了许多新特性,包括语法糖、新数据类型、模块化支持等,显著提升了开发效率和代码可维护性。 核心知识点概览 变量声明 let 和 const 取代 var…...
)
.Net Framework 4/C# 关键字(非常用,持续更新...)
一、is 关键字 is 关键字用于检查对象是否于给定类型兼容,如果兼容将返回 true,如果不兼容则返回 false,在进行类型转换前,可以先使用 is 关键字判断对象是否与指定类型兼容,如果兼容才进行转换,这样的转换是安全的。 例如有:首先创建一个字符串对象,然后将字符串对象隐…...

C/C++ 中附加包含目录、附加库目录与附加依赖项详解
在 C/C 编程的编译和链接过程中,附加包含目录、附加库目录和附加依赖项是三个至关重要的设置,它们相互配合,确保程序能够正确引用外部资源并顺利构建。虽然在学习过程中,这些概念容易让人混淆,但深入理解它们的作用和联…...

Golang——6、指针和结构体
指针和结构体 1、指针1.1、指针地址和指针类型1.2、指针取值1.3、new和make 2、结构体2.1、type关键字的使用2.2、结构体的定义和初始化2.3、结构体方法和接收者2.4、给任意类型添加方法2.5、结构体的匿名字段2.6、嵌套结构体2.7、嵌套匿名结构体2.8、结构体的继承 3、结构体与…...

消防一体化安全管控平台:构建消防“一张图”和APP统一管理
在城市的某个角落,一场突如其来的火灾打破了平静。熊熊烈火迅速蔓延,滚滚浓烟弥漫开来,周围群众的生命财产安全受到严重威胁。就在这千钧一发之际,消防救援队伍迅速行动,而豪越科技消防一体化安全管控平台构建的消防“…...

es6+和css3新增的特性有哪些
一:ECMAScript 新特性(ES6) ES6 (2015) - 革命性更新 1,记住的方法,从一个方法里面用到了哪些技术 1,let /const块级作用域声明2,**默认参数**:函数参数可以设置默认值。3&#x…...

若依登录用户名和密码加密
/*** 获取公钥:前端用来密码加密* return*/GetMapping("/getPublicKey")public RSAUtil.RSAKeyPair getPublicKey() {return RSAUtil.rsaKeyPair();}新建RSAUti.Java package com.ruoyi.common.utils;import org.apache.commons.codec.binary.Base64; im…...

ThreadLocal 源码
ThreadLocal 源码 此类提供线程局部变量。这些变量不同于它们的普通对应物,因为每个访问一个线程局部变量的线程(通过其 get 或 set 方法)都有自己独立初始化的变量副本。ThreadLocal 实例通常是类中的私有静态字段,这些类希望将…...
