数据结构【图的类型定义和存储结构】
数据结构之图
- 图的定义和概念
- 图的定义
- 图的术语
- 图的类型定义
- 图的存储结构
- 数组(邻接矩阵)表示法
- 无向图的邻接矩阵表示法
- 有向图的邻接矩阵表示法
- 网(即有权图)的邻接矩阵表示法
- 邻接矩阵的ADT定义
- 邻接表(链式)表示法
- 无向图
- 有向图
- 图的邻接表存储表示
- 邻接表操作
- 邻接表表示无向网
图的定义和概念
图的定义
图(Graph)是由顶点的有穷非空集合和顶点之间边的集合组成,通常表示为:G(V,E)。
其中,G表示一个图,V 是图 G 中顶点的有穷非空集合,E 是图 G 中边的有穷集合。
图形结构是多对多的关系。
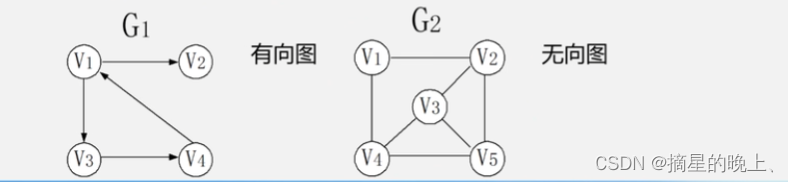
无向图:每条边都是无方向的。
有向图:每条边都是有方向的。
特殊:
当线性表没有数据节点时,线性表为空表。 树中没有节点时,树为空树。
但是,在图中不允许没有顶点,但是可以没有边。
完全图:任意两个点都有一条边相连。
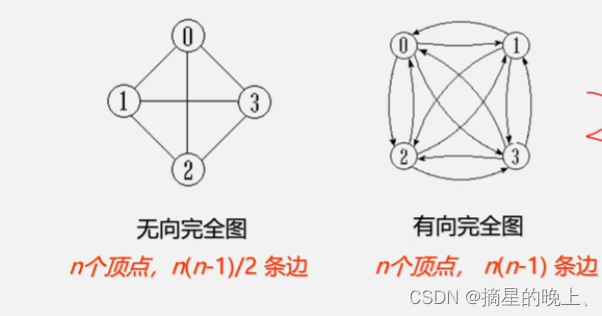
稀疏图:有很少边或弧的图(e<nlogn)。
稠密图:有较多边或弧的图。
图的术语
网:边/弧带权的图
邻接:
有边/弧相连的两个顶点之间的关系。
存在(Vi,Vj),则称Vi和Vj互为邻接点;
存在<Vi,Vj>,则称Vi邻接到Vj;, Vj邻接于Vi。
关联/依附:边/弧与顶点之间的关系。
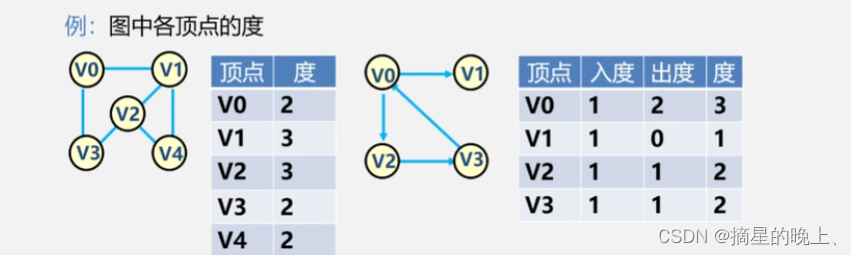
顶点的度:
与该顶点相关联的边的数目,记为TD(v)。
在有向图中,顶点的度等于该顶点的入度与出度之和。
顶点 v 的入度是以 v 为终点的有向边的条数记作ID(v)。
顶点 v 的出度是以 v 为始点的有向边的条数记作 OD(v)。
有向图中顶点的度 = 入度 + 出度。
即 TD(V) = ID(V) + OD(V)。
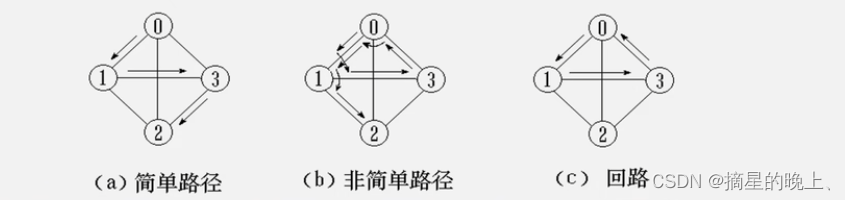
路径:接续的边构成的顶点序列。
路径长度: 路径上边或弧的数目/权值之和。
回路(环): 第一个顶点和最后一个顶点相同的路径。
简单路径: 除路径起点和终点可以相同外,其余顶点均不相同的路径。
简单回路(简单环): 除路径起点和终点相同外,其余顶点均不相同的路径。
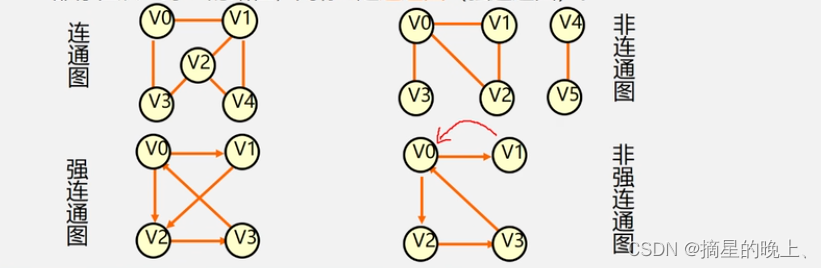
连通图:在无 (有) 向图G=( V, E) )中,若对任何两个顶点 v、u都存在从v 到 u 的路径,则称G是连通图 (强连通图)
权与网:
图中边或弧所具有的相关数称为权。表明从一个顶点到另一个顶点的距离或耗费。
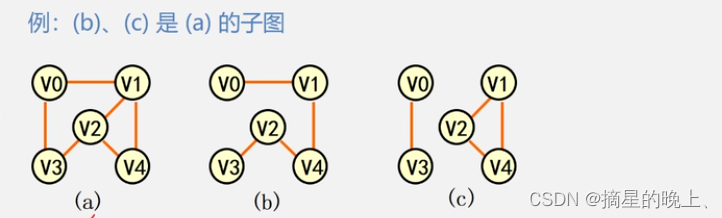
子图:
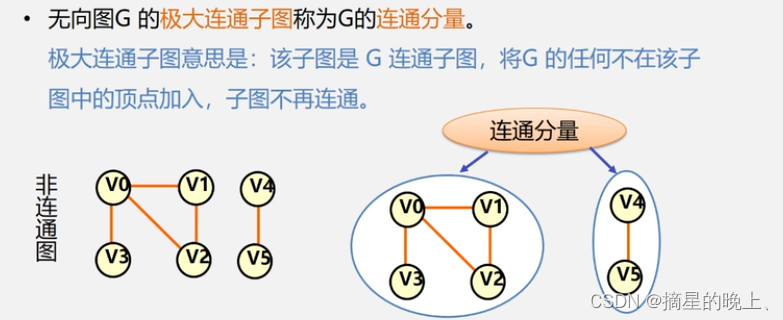
连通分量(强连通分量):
无向图中的连通分量:
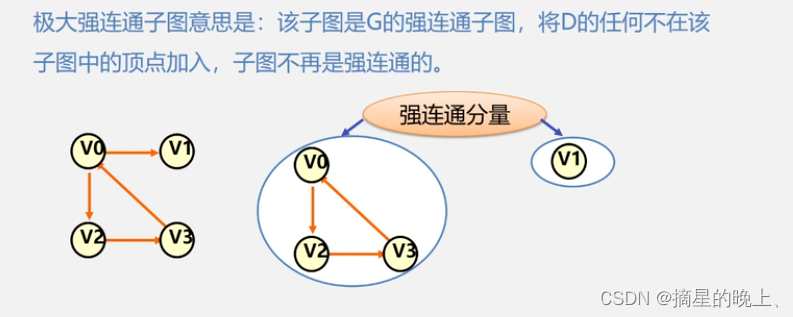
有向图中的强连通分量:
有向图G中的极大强连通子图称为G的强连通分量。
极小连通子图:
该子图是G的连通子图,在该子图中删除任何一条连通路径,子图不再连通。
生成树:包含无向图G的所有定点的极小连通子图。
生成森林:对非连通图,由各个连通分量的生成树的集合。

图的类型定义

基本操作P:
Create_Graph(&G,V,VR) : 图的创建操作
初始条件:无。
操作结果: 生成一个没有顶点的空图G。
GetVex(G,v) : 求图中的顶点v的值
初始条件: 图G存在,v是图中的一个顶点。
操作结果: 生成一个没有顶点的空图G
CreateGraph(&G,V,VR)
初始条件: V是图的顶点集,VR是图中弧的集合
操作结果: 按V和VR的定义 构造图G
DFSTraverse(G)
初始条件:图G存在
操作结果:对图进行深度优先遍历
BFSTraverse(G)
初始条件:图G存在
操作结果: 对图进行广度优先遍历
图的存储结构
图的逻辑结构:多对多
图没有顺序存储结构,但是可以用二维数组来表示元素间的关系。
链式存储结构:有数组表示法和邻接表(多重链表)表示法
数组(邻接矩阵)表示法
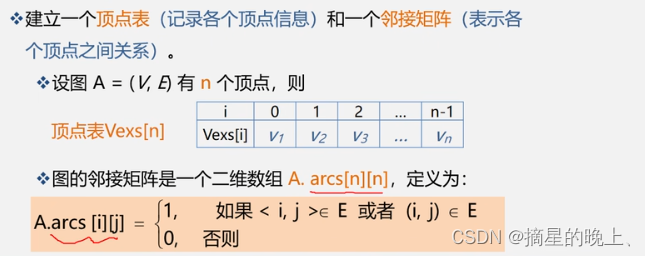
邻接矩阵的好处:
- 直观、简单、好理解 方便检查任意一对顶点间是否存在边
- 方便找任一顶点的所有“邻接点”(有边直接相连的顶点)
- 方便计算任一顶点的“度”(从该点发出的边数为“出度”,指向该点的边数为“入度”)
– 无向图:对应行(或列)非0元素的个数
– 有向图:对应行非0元素的个数是“出度”,对应列非0元素的个数是“入度
无向图的邻接矩阵表示法

完全图的邻接矩阵中,对角元素为0,其余1。
有向图的邻接矩阵表示法
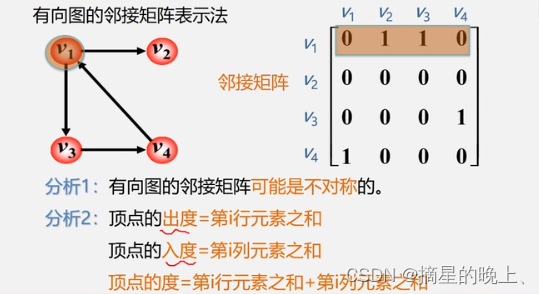
网(即有权图)的邻接矩阵表示法
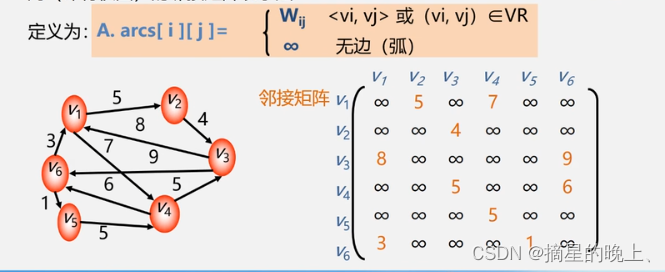
邻接矩阵的ADT定义

用邻接矩阵表示法创建无向网



在图中查找顶点:
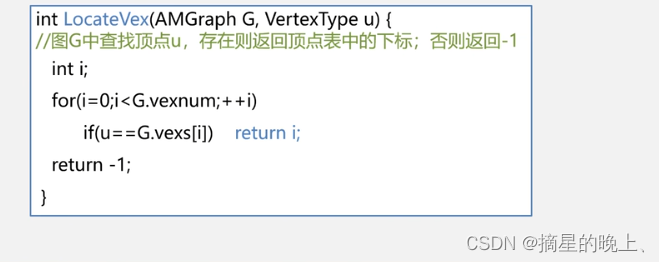
邻接表(链式)表示法
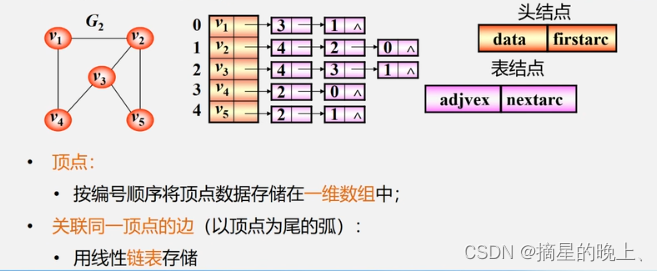
无向图
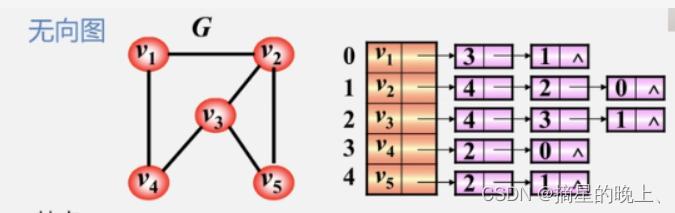
特点:
- 邻接表不唯一
- 若无向图中有 n 个顶点、e 条边,则其邻接表需 n 个头结点和2e 个表结点。适宜存储稀疏图。
- 无向图中顶点v的度为第i个单链表中的结点数。
有向图
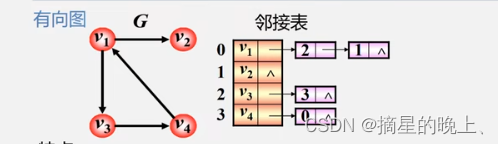
特点:
- 找出度易,找入度难。
- 顶点 v 的出度为第i个单链表中的结点个数。
- 顶点 v 的入度为整个单链表中邻接点域值是i-1的结点个数。
逆邻接表则相反
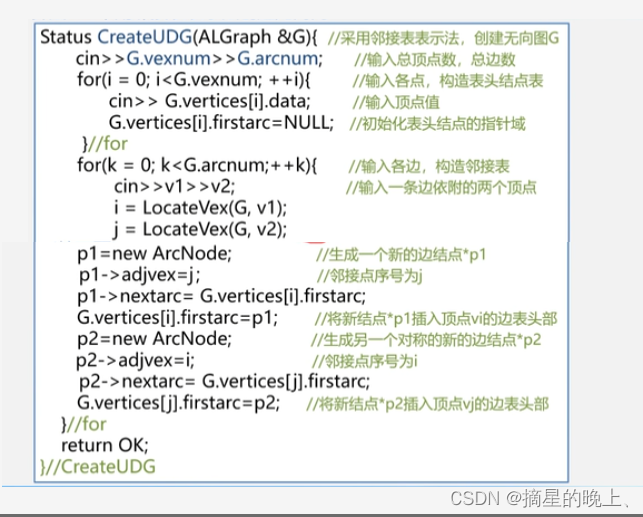
图的邻接表存储表示



邻接表操作
ALGraghG; //定义了邻接表表示的图G
G.vexum=5; G.arcnum=5; //图G包含5个顶点,5条边
G.vertices[1].data= 'b' //图G中第2个顶点是b
p=G.vertices[1].firtarc; //指针p指向顶点b的第一条边结点
p->adjvex =4; //p指针所指边结点是到下标为4的结点的边
邻接表表示无向网
(1)输入总顶点数和总边数
(2)建立顶点表,依次输入点的信息存入顶点表中,使每个表头结点的指针域初始化为NULL
(3)创建邻接表,依次输入每条边依附的两个顶点,确定两个顶点的序号和,建立边结点,将此边结点分别插入到vi和vj对应的两个边链表的头部
参考资料:数据结构与算法基础-王卓老师
相关文章:

数据结构【图的类型定义和存储结构】
数据结构之图 图的定义和概念图的定义图的术语 图的类型定义图的存储结构数组(邻接矩阵)表示法无向图的邻接矩阵表示法有向图的邻接矩阵表示法网(即有权图)的邻接矩阵表示法 邻接矩阵的ADT定义邻接表(链式)…...

PHP Smarty如何进行调试和错误处理?
欢迎来到PHP Smarty的世界。如果你在这里寻求如何调试和错误处理的方法,那么我可以向你保证,我们会让这个过程尽可能的有趣和轻松。 首先,让我们先来谈谈调试。在Smarty中,你可以使用以下几种方法来进行调试: 使用Sm…...

手搓vue3组件_0,打包配置
打包后引入项目是发现报错: Cannot read properties of null (reading isCE) TypeError: Cannot read properties of null (reading isCE)这个是由于vue版本冲突问题, 这里我引入了自己打包的ui组件库,但是ui组件库中打包进入了自己的vue,那么在此时使用时,如果你引入的自己的组…...

WebAssembly
WebAssembly(简称Wasm)是一种面向Web的二进制指令格式,用于在现代Web浏览器中运行高性能的可移植代码。它是一种跨平台、低级别的虚拟机技术,允许开发者将不同编程语言的代码编译成Wasm格式,然后在Web浏览器中运行。 …...
--- LED闪烁,滴答定时器精准延时)
TM4C123库函数学习(2)--- LED闪烁,滴答定时器精准延时
前言 (1)阅读本文之前,需要先看TM4C123库函数学习(1)— 点亮LEDTM4C123的ROM函数简介keil开发环境搭建篇。 (2)TM4C123是M4的内核,拥有一个24位向下计数的SysTick定时器。࿰…...

Linux: network: tcp: back-off技术
当一个包需要重传的时候,会使用 exponential back-off来计算下一次重传的时间。 这个back-off的使用还是相当的广泛:《Adaptive Backoff Synchronization Technique》https://dl.acm.org/doi/pdf/10.1145/74926.74970 The general idea of backoff has …...

36 | 银行贷款数据分析
本文将以银行贷款数据分析为主题,深入探讨如何运用数据科学的方法,揭示银行贷款领域的内在规律和趋势。通过对贷款数据的分析,我们能够洞察不同类型贷款的分布情况、贷款金额的变化趋势,以及借款人的特征和还款情况等关键信息。 通过运用Python编程语言及相关的数据分析工…...

计算机网络-物理层(二)- 传输方式
计算机网络-物理层(二)- 传输方式 串型传输与并行传输 串行传输:是指数据是一个比特一个比特依次发送的,因此在发送端和接收端之间,只需要一条数据传输线路即可 并行传输:是指一次发送n个比特而不是一个比特,因此发送…...

超强台风“杜苏芮”来袭!如何实现安全可靠的通信?
暴雨来袭 超强台风“杜苏芮”是2023年太平洋台风季第5个被命名的台风,在我国东南沿海地区造成了巨大的影响,在7月28日登录福建省晋江市时,“杜苏芮”中心附近最大风力15级,达到了超强台风的等级;福州市区、闽侯、莆田…...
内网隧道—HTTP\DNS\ICMP
本文仅限于安全研究和学习,用户承担因使用此工具而导致的所有法律和相关责任! 作者不承担任何法律和相关责任! HTTP隧道 Neo-reGeorg Neo-reGeorg 是一个旨在积极重构 reGeorg 的项目,目的是: 提高可用性࿰…...
QT mouseTracking
在Qt中要捕捉鼠标移动事件需要重写MouseMoveEvent,但是MouseMoveEvent为了不太耗资源在默认状态下是要鼠标按下才能捕捉到。要想鼠标不按下时的移动也能捕捉到,需要setMouseTracking(true)。 如果鼠标跟踪失效(默认),…...

java操作mongdb【超详细】
Java操作 搭建 搭建 依赖 <!--mongodb--><dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-data-mongodb</artifactId></dependency>配置文件 spring:data:mongodb:host…...
JavaScript函数
什么是函数? 在 JavaScript 中,函数是一段被封装起来用于特定任务的可重复使用的代码块。 例如: function logger() {console.log(IT知识一享); }这样就创造了logger()函数,后续可以重复利用这个函数让它输出日志,后…...

RISC-V公测平台发布 · 使用YCSB测试SG2042上的MySQL性能
实验介绍: YCSB(全称为Yahoo! Cloud Serving Benchmark),该性能测试工具由Java语言编写(在之前的MC文章中也提到过这个,如果没看过的读者可以去看看之前MC那一期),主要用于云端或者…...
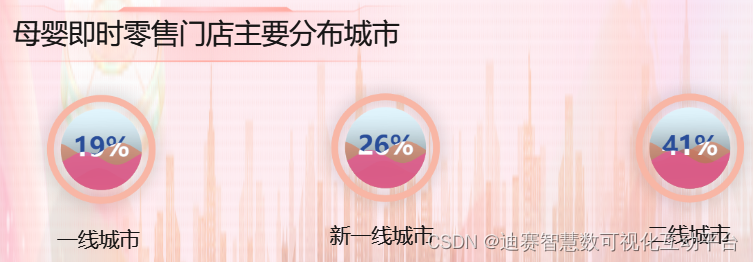
母婴即时零售行业数据可视化分析
对新晋父母来说,很多母婴用品如同一位贴心的助手,为他们的宝宝提供温暖和呵护。从婴儿床垫到可爱的拼图玩具,每一件用品都是为宝宝的成长和发展量身定制。对于繁忙的父母们而言,这些用品不仅帮助照顾孩子,更是为他们减…...

快速解决IDEA中类的图标变成J,不是C的情况
有时候导入新的项目后,会出现如下情况,类的图标变成J,如图: 直接上解决方法: 找到项目的pom.xml,右键,在靠近最下方的位置找到Add as Maven Project,点击即可。 此时,一般类的图标就…...

vue学习笔记
1.官网 v2官网 https://v2.cn.vuejs.org/ v3官网 https://cn.vuejs.org/ 2.vue引入 在线引入 <script src"https://cdn.jsdelivr.net/npm/vue2.7.14/dist/vue.js"></script> 下载引入(下载链接) https://v2.cn.vuejs.org/js/vue.js 3.初始化渲…...
难解的bug
android.app.RemoteServiceException: Context.startForegroundService() did not then call Service.startForeground(): ServiceRecord 【Android TimeCat】 解决 context.startforegroundservice() did not then call service.startforeground() | XiChens Blog http://www…...

人文景区有必要做VR云游吗?如何满足游客出行需求?
VR云游在旅游行业中的应用正在快速增长,为游客带来沉浸式体验的同时,也为文旅景区提供了新的营销方式。很多人说VR全景展示是虚假的,比不上真实的景区触感,人文景区真的有必要做VR云游吗?我的答案是很有必要。 如果你认…...
【字节跳动青训营】后端笔记整理-1 | Go语言入门指南:基础语法和常用特性解析
**本人是第六届字节跳动青训营(后端组)的成员。本文由博主本人整理自该营的日常学习实践,首发于稀土掘金:🔗Go语言入门指南:基础语法和常用特性解析 | 青训营 本文主要梳理自第六届字节跳动青训营ÿ…...

日语AI面试高效通关秘籍:专业解读与青柚面试智能助攻
在如今就业市场竞争日益激烈的背景下,越来越多的求职者将目光投向了日本及中日双语岗位。但是,一场日语面试往往让许多人感到步履维艰。你是否也曾因为面试官抛出的“刁钻问题”而心生畏惧?面对生疏的日语交流环境,即便提前恶补了…...

docker详细操作--未完待续
docker介绍 docker官网: Docker:加速容器应用程序开发 harbor官网:Harbor - Harbor 中文 使用docker加速器: Docker镜像极速下载服务 - 毫秒镜像 是什么 Docker 是一种开源的容器化平台,用于将应用程序及其依赖项(如库、运行时环…...

23-Oracle 23 ai 区块链表(Blockchain Table)
小伙伴有没有在金融强合规的领域中遇见,必须要保持数据不可变,管理员都无法修改和留痕的要求。比如医疗的电子病历中,影像检查检验结果不可篡改行的,药品追溯过程中数据只可插入无法删除的特性需求;登录日志、修改日志…...

在rocky linux 9.5上在线安装 docker
前面是指南,后面是日志 sudo dnf config-manager --add-repo https://download.docker.com/linux/centos/docker-ce.repo sudo dnf install docker-ce docker-ce-cli containerd.io -y docker version sudo systemctl start docker sudo systemctl status docker …...

Day131 | 灵神 | 回溯算法 | 子集型 子集
Day131 | 灵神 | 回溯算法 | 子集型 子集 78.子集 78. 子集 - 力扣(LeetCode) 思路: 笔者写过很多次这道题了,不想写题解了,大家看灵神讲解吧 回溯算法套路①子集型回溯【基础算法精讲 14】_哔哩哔哩_bilibili 完…...

安宝特方案丨XRSOP人员作业标准化管理平台:AR智慧点检验收套件
在选煤厂、化工厂、钢铁厂等过程生产型企业,其生产设备的运行效率和非计划停机对工业制造效益有较大影响。 随着企业自动化和智能化建设的推进,需提前预防假检、错检、漏检,推动智慧生产运维系统数据的流动和现场赋能应用。同时,…...

SCAU期末笔记 - 数据分析与数据挖掘题库解析
这门怎么题库答案不全啊日 来简单学一下子来 一、选择题(可多选) 将原始数据进行集成、变换、维度规约、数值规约是在以下哪个步骤的任务?(C) A. 频繁模式挖掘 B.分类和预测 C.数据预处理 D.数据流挖掘 A. 频繁模式挖掘:专注于发现数据中…...

令牌桶 滑动窗口->限流 分布式信号量->限并发的原理 lua脚本分析介绍
文章目录 前言限流限制并发的实际理解限流令牌桶代码实现结果分析令牌桶lua的模拟实现原理总结: 滑动窗口代码实现结果分析lua脚本原理解析 限并发分布式信号量代码实现结果分析lua脚本实现原理 双注解去实现限流 并发结果分析: 实际业务去理解体会统一注…...

BCS 2025|百度副总裁陈洋:智能体在安全领域的应用实践
6月5日,2025全球数字经济大会数字安全主论坛暨北京网络安全大会在国家会议中心隆重开幕。百度副总裁陈洋受邀出席,并作《智能体在安全领域的应用实践》主题演讲,分享了在智能体在安全领域的突破性实践。他指出,百度通过将安全能力…...
)
是否存在路径(FIFOBB算法)
题目描述 一个具有 n 个顶点e条边的无向图,该图顶点的编号依次为0到n-1且不存在顶点与自身相连的边。请使用FIFOBB算法编写程序,确定是否存在从顶点 source到顶点 destination的路径。 输入 第一行两个整数,分别表示n 和 e 的值(1…...
