Codeforces Round #822 (Div. 2)
A(签到) - Select Three Sticks
题意:
给你一个长度为 n 的正整数序列,你可以操作任意次,每一次操作可以选择任意一个元素,把它 + 1 或者 - 1,问最少多少次操作可以使得序列中存在三个相同的数字以构成一个等边三角形.
思路:
先 sort 一遍,然后取 min 即可.
参考代码:
void solve() {int n;std::cin >> n;std::vector<int> a(n);for (int i = 0; i < n; i++) {std::cin >> a[i];}std::sort(a.begin(), a.end());int min = (1 << 31) - 1;for (int i = 2; i < n; i++) {min = std::min(min, a[i] - a[i - 2]);}std::cout << min << "\n";
}B(找规律) - Bright, Nice, Brilliant
题意:
给定一个三角形的金字塔,点亮一部分的砖块,使得每一层的砖块的亮度等于当前层(从高往低),请构造出一种解使得金字塔满足要求。一个点亮的砖块可以将光传递到下面两个砖块中,一个砖块的亮度为所有能够传递光的砖的数量。
思路:
我们找规律可以发现,只需要让最两侧,也就是金字塔的最外一层点亮,即可让所有砖块的亮度等于当前层数。
参考代码:
void solve() {int n;std::cin >> n;for (int i = 1; i <= n; i++) {if (i == 1) {std::cout << "1\n";continue;}std::cout << "1 ";for (int j = 1; j <= i - 2; j++) {std::cout << "0\n";}std::cout << "1\n";}
}C (贪心) - Removing Smallest Multiples
题意:
有集合 S = {1,2,⋯,n}, T,每次操作你可以选择一个 K,然后删除集合中最小且为K的倍数,代价为 K,问最少需要多少代价,能让S变成T。
思路:
贪心。从小枚举每个k,让k尽量取多次,直到遇到一个位置不能删。
参考代码:
void solve() {int n;std::string t;std::cin >> n >> t;ll ans{};for (int i = 1; i <= n; i++) {for (int j = i; j <= n; j+=i) {if (t[j - 1] == '1') {break;}if (t[j - 1] == '0') {t[j - 1] = '2';ans += i;}}}std::cout << ans << "\n";
}D(贪心 + 双指针) - Slime Escape
题意:
给定一个数组 a。初始位置为k,血量HP为0。每次可以向右或者向左移动。每到达一个位置,会改变HP增加当前对应位置的值,多次经过一个位置只有第一次会改变HP的值,ai可能是正或者负数,表示HP增加和减少。当HP变成负数时,你就会挂掉。问能否走出两端中的其中一端。
思路:
贪心+双指针。两种情况是对称的,只需考虑一端出去的情况。不妨设,从右端出去。
每次向右边移动一个位置,就看看左边所有能到达的位置中,能获得的最大血量,则当前能增加的最大血量等于 max(前一个位置能增加的最大血量,当前位置能增加的血量)。
记j为左边能到达的位置,maxval为从k - 1到j中增加的最大血量,left等于a[j]到a[k - 1]的和,i为右边到达的当前位置,right为a[k]到a[i]的和。
maxval即为从k移动到i的过程中,能从左边获取得到的最大的生命值。
结论1,如果i - 1能到达maxval所在的位置,则i也能到达该位置 只需在i之前先到达该位置即可。
结论2,我们只需关注right非减的位置(最长非减序列),假设这些位置为ps。则maxval只有在属于ps的位置才有可能改变。如果某个位置i不在ps中,则能到达i当且仅当right + maxval >= 0且i - 1可达,我们只需关注x + 1,x+1不属于ps的情况,此时可以从x出发到达maxval所在的位置,而到达x+1时整体血量减少,不可能移动到x能到达的位置的更左端。
结论3,y时ps中x的下一个位置,则x能到达的位置,y也能到达。
因此,我们可以双指针进行。i从k开始枚举,对每个i,j依据条件向左移动,同时维护maxval即可。
参考代码:
bool f(std::vector<ll> &a, int k) {ll left = 0, right = 0, maxval = 0;for (int i = k, j = k; i < a.size(); i++) {right += a[i];if (right + maxval < 0) {return false;}while (j - 1 >= 0 && left + a[j - 1] + right >= 0) {left += a[--j];maxval = std::max(maxval, left);}}return true;
}void solve() {int n, k;std::cin >> n >> k;std::vector<ll> a(n);for (int i = 0; i < n; i++) {std::cin >> a[i];}if (k == 1 || k == n || f(a, k - 1)) {std::cout << "Yes\n";return;}std::reverse(a.begin(), a.end());std::cout << (f(a, n - k) ? "Yes" : "No") << "\n";
}相关文章:
)
Codeforces Round #822 (Div. 2)
A(签到) - Select Three Sticks 题意: 给你一个长度为 n 的正整数序列,你可以操作任意次,每一次操作可以选择任意一个元素,把它 1 或者 - 1,问最少多少次操作可以使得序列中存在三个相同的数字以构成一个等边三角形.…...
)
华为OD机试 - 最短木板长度(JS)
最短木板长度 题目 小明有 n n n块木板,第 i i i(1≤ i i </...
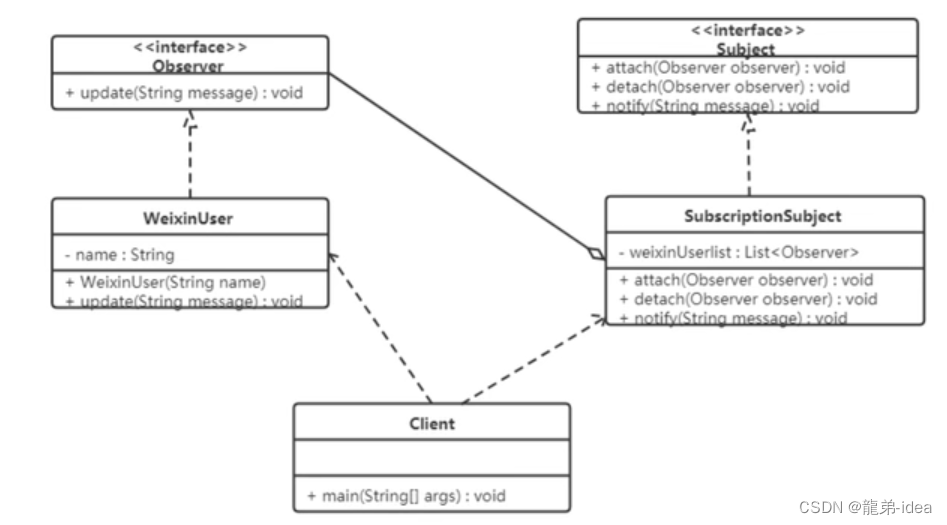
java设计模式——观察者模式
概述 定义:又被称为发布-订阅(Publish/Subscribe)模式,它定义了一种一对多的依赖关系,让多个观察者对象同时监听某一个主题对象。这个主题对象在状态变化时,会通知所有的观察者对象,使他们能够自动更新自己。 结构 在观察者模式…...
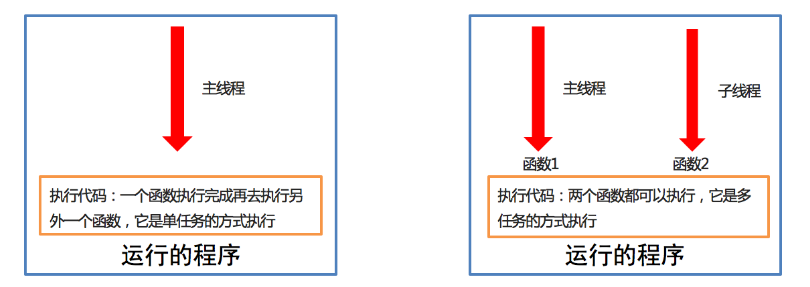
linux高级命令之线程的注意点
线程的注意点学习目标能够说出线程的注意点1. 线程的注意点介绍线程之间执行是无序的主线程会等待所有的子线程执行结束再结束线程之间共享全局变量线程之间共享全局变量数据出现错误问题2. 线程之间执行是无序的import threading import timedeftask():time.sleep(1)print(&qu…...
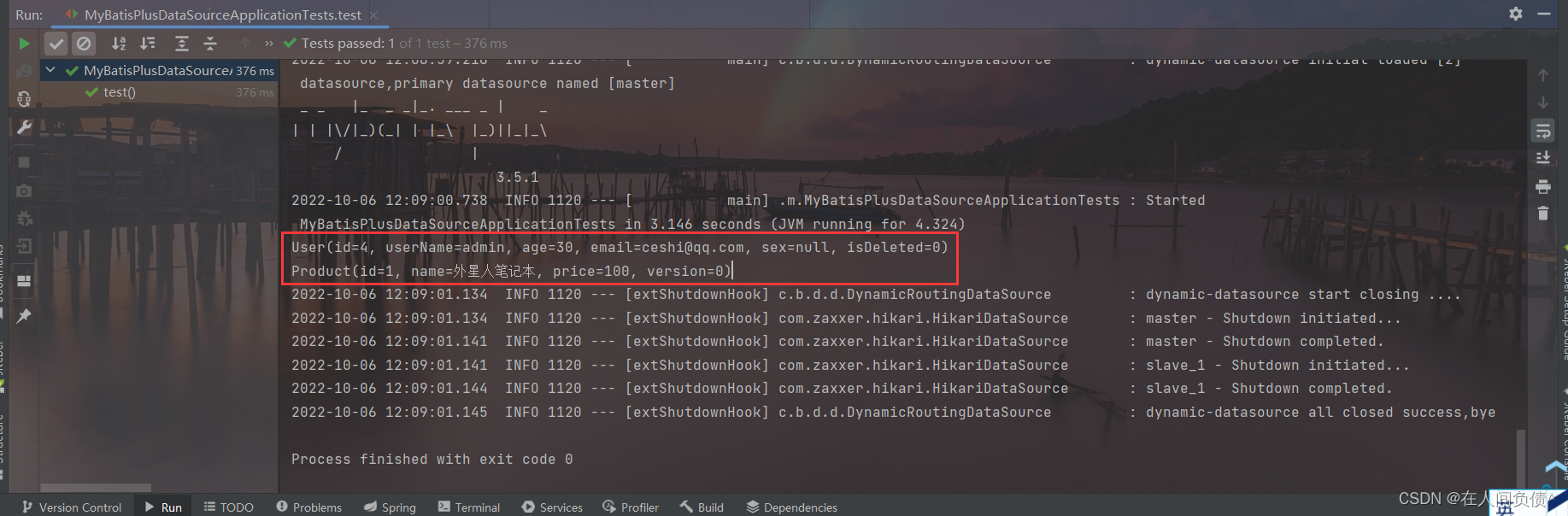
MyBatisPlus ---- 多数据源
MyBatisPlus ---- 多数据源1. 创建数据库及表2. 引入依赖3. 配置多数据源4. 创建用户service5. 创建商品service6. 测试适用于多种场景:纯粹多库、读写分离、一主多从、混合模式等 目前我们就来模拟一个纯粹多库的一个场景,其他场景类似 场景说明&#x…...

Java多线程
目录1 多线程1.1 进程1.2 线程1.3 多线程的实现方式1.3.1 方式1:继承Tread类1.3.2 方式2:实现Runnable接口1.3.3 方式3:实现Callable接口1.4 设置和获取线程名称1.5 线程调度1.6 线程控制1.7 线程生命周期1.8 数据安全问题之案例:…...
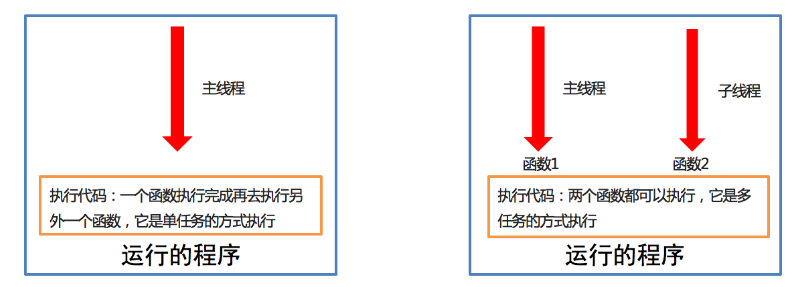
linux高级命令之线程执行带有参数的任务
线程执行带有参数的任务学习目标能够写出线程执行带有参数的任务1. 线程执行带有参数的任务的介绍前面我们使用线程执行的任务是没有参数的,假如我们使用线程执行的任务带有参数,如何给函数传参呢?Thread类执行任务并给任务传参数有两种方式:args 表示以…...
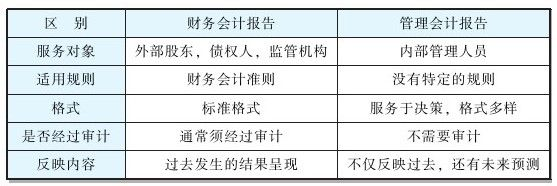
管理会计报告和财务报告的区别
财务会计报告是给投资人看的,可以反映公司总体的盈利能力。不过,我们回顾一下前面“第一天”里面提到的问题。如果你是公司的产品经理,目前有三个产品在你的管辖范围内。上级给你一笔新的资金,这笔资金应该投到哪个产品上…...
 | 机试题算法思路 【2023】)
华为OD机试 - 最左侧冗余覆盖子串(Python) | 机试题算法思路 【2023】
最近更新的博客 华为OD机试 - 自动曝光(Python) | 机试题算法思路 【2023】 华为OD机试 - 双十一(Python) | 机试题算法思路 【2023】 华为OD机试 - 删除最少字符(Python) | 机试题算法思路 【2023-02】 华为OD机试 - Excel 单元格数值统计(Python) | 机试题算法思路 …...
【Opencv 系列】第1章 图像基础
通过本套课程,可以学到: 1.opencv的基本操作 2.两个案例,目标追踪&人脸识别 对重点内容,我会提示,包括我再准备这套课程过程中遇到的坑点! 最后代码我会放到git上,章节顺序一致:https://github.com/justinge/opencv_tutorial.git 系列文章目录 第1章 Opencv 图像基础 和 …...

创建和销毁对象——遇到多个构造器参数时要考虑使用构建器
静态工厂和构造器有个共同的局限性:它们都不能很好地扩展到大量的可选参数。比如用一个类表示包装食品外面显示的营养成分标签。这些标签中有几个域是必需的:每份的含量、每罐的含量以及每份的卡路里。还有超过20个的可选域:总脂肪量、饱和脂…...

【c++学习】入门c++(中)
目录一. 前言二. 函数重载1. 概念2.函数名修饰规则三 .引用(&)1. 概念2. 引用特性3.应用1.做参数2. 做返回值3. 传值、传引用效率比较4.引用和指针的区别四 . 结语一. 前言 小伙伴们大家好,今天我们继续学习c入门知识,今天的…...
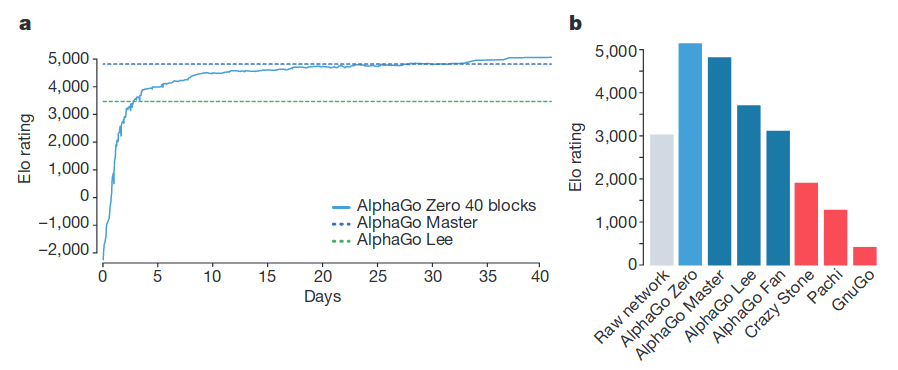
论文阅读_AlphaGo_Zero
论文信息 name_en: Mastering the game of Go without human knowledge name_ch: 在没有人类知识的情况下掌握围棋游戏 paper_addr: http://www.nature.com/articles/nature24270 doi: 10.1038/nature24270 date_publish: 2017-10-01 tags: [‘深度学习’,‘强化学习’] if: 6…...

一文教你用Python创建自己的装饰器
python装饰器在平常的python编程中用到的还是很多的,在本篇文章中我们先来介绍一下python中最常使用的staticmethod装饰器的使用。 目录一、staticmethod二、自定义装饰器python类实现装饰器python函数嵌套实现装饰器多个装饰器调用三、带参数的装饰器一、staticmet…...
)
华为OD机试 - 任务总执行时长(JS)
任务总执行时长 题目 任务编排服务负责对任务进行组合调度。参与编排的任务又两种类型,其中一种执行时长为taskA,另一种执行时长为taskB。任务一旦开始执行不能被打断,且任务可连续执行。服务每次可以编排num个任务。 请编写一个方法,生成每次编排后的任务所有可能的总执…...
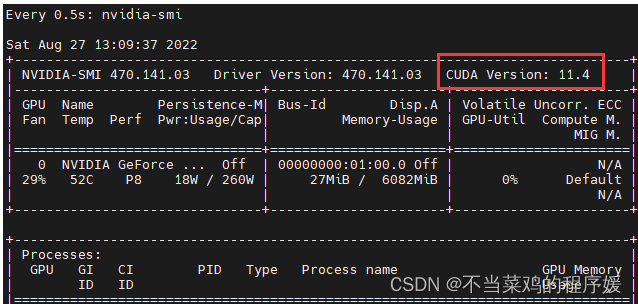
pytorch离线快速安装
1.pytorch官网查看cuda版本对应的torch和torchvisionde 版本(ncvv -V,nvidia-sim查看cuda对应的版本) 2.离线下载对应版本,网址https://download.pytorch.org/whl/torch_stable.html 我下载的: cu113/torch-1.12.0%2Bcu113-cp37-cp37m-win_…...
)
华为OD机试 - 数组合并(JS)
数组合并 题目 现在有多组整数数组,需要将他们合并成一个新的数组。 合并规则,从每个数组里按顺序取出固定长度的内容合并到新的数组中, 取完的内容会删除掉, 如果该行不足固定长度或者已经为空, 则直接取出剩余部分的内容放到新的数组中,继续下一行。 如样例1,获得长度3,先遍…...

不要让GPT成为你通向“学业作弊”的捷径——使用GPT检测工具来帮助你保持正确的方向
不要让GPT成为你通向“学业作弊”的捷径——使用GPT检测工具来帮助你保持正确的方向 最近,多所美国高校以及香港大学等都明确禁止在校使用ChatGPT等智能文本生成工具。GPT(Generative Pre-trained Transformer)是一种自然语言处理技术&#x…...
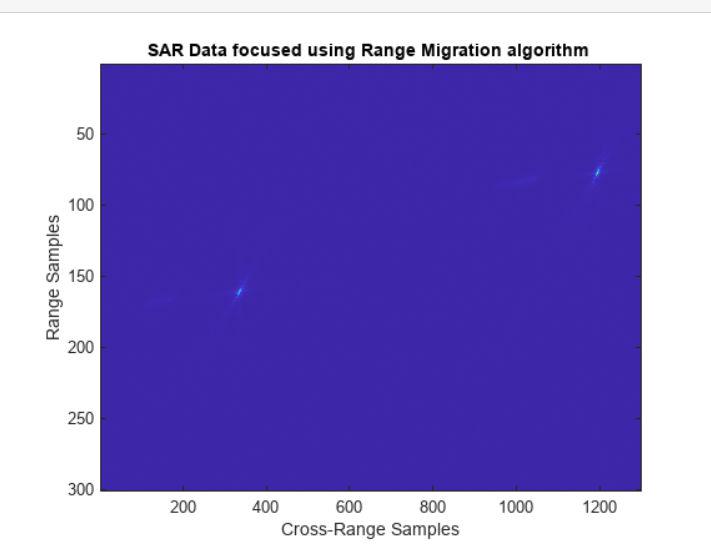
基于matlab的斜视模式下SAR建模
一、前言此示例说明如何使用线性 FM (LFM) 波形对基于聚光灯的合成孔径雷达 (SAR) 系统进行建模。在斜视模式下,SAR平台根据需要从宽侧斜视一定角度向前或向后看。斜视模式有助于对位于当前雷达平台位置前面的区域进行…...

15-基础加强-1-类加载器反射
文章目录1.类加载器1.1类加载器【理解】1.2类加载的过程【理解】1.3类加载的分类【理解】1.4双亲委派模型【理解】1.5ClassLoader 中的两个方法【应用】2.反射2.1反射的概述【理解】2.2获取Class类对象的三种方式【应用】 第1步:获取类的Class对象2.3反射获取构造方…...

测试微信模版消息推送
进入“开发接口管理”--“公众平台测试账号”,无需申请公众账号、可在测试账号中体验并测试微信公众平台所有高级接口。 获取access_token: 自定义模版消息: 关注测试号:扫二维码关注测试号。 发送模版消息: import requests da…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(二)
HoST框架核心实现方法详解 - 论文深度解读(第二部分) 《Learning Humanoid Standing-up Control across Diverse Postures》 系列文章: 论文深度解读 + 算法与代码分析(二) 作者机构: 上海AI Lab, 上海交通大学, 香港大学, 浙江大学, 香港中文大学 论文主题: 人形机器人…...

遍历 Map 类型集合的方法汇总
1 方法一 先用方法 keySet() 获取集合中的所有键。再通过 gey(key) 方法用对应键获取值 import java.util.HashMap; import java.util.Set;public class Test {public static void main(String[] args) {HashMap hashMap new HashMap();hashMap.put("语文",99);has…...

unix/linux,sudo,其发展历程详细时间线、由来、历史背景
sudo 的诞生和演化,本身就是一部 Unix/Linux 系统管理哲学变迁的微缩史。来,让我们拨开时间的迷雾,一同探寻 sudo 那波澜壮阔(也颇为实用主义)的发展历程。 历史背景:su的时代与困境 ( 20 世纪 70 年代 - 80 年代初) 在 sudo 出现之前,Unix 系统管理员和需要特权操作的…...

Hive 存储格式深度解析:从 TextFile 到 ORC,如何选对数据存储方案?
在大数据处理领域,Hive 作为 Hadoop 生态中重要的数据仓库工具,其存储格式的选择直接影响数据存储成本、查询效率和计算资源消耗。面对 TextFile、SequenceFile、Parquet、RCFile、ORC 等多种存储格式,很多开发者常常陷入选择困境。本文将从底…...

MacOS下Homebrew国内镜像加速指南(2025最新国内镜像加速)
macos brew国内镜像加速方法 brew install 加速formula.jws.json下载慢加速 🍺 最新版brew安装慢到怀疑人生?别怕,教你轻松起飞! 最近Homebrew更新至最新版,每次执行 brew 命令时都会自动从官方地址 https://formulae.…...

聚六亚甲基单胍盐酸盐市场深度解析:现状、挑战与机遇
根据 QYResearch 发布的市场报告显示,全球市场规模预计在 2031 年达到 9848 万美元,2025 - 2031 年期间年复合增长率(CAGR)为 3.7%。在竞争格局上,市场集中度较高,2024 年全球前十强厂商占据约 74.0% 的市场…...

基于 HTTP 的单向流式通信协议SSE详解
SSE(Server-Sent Events)详解 🧠 什么是 SSE? SSE(Server-Sent Events) 是 HTML5 标准中定义的一种通信机制,它允许服务器主动将事件推送给客户端(浏览器)。与传统的 H…...
: 发布订阅模式)
JS设计模式(5): 发布订阅模式
解锁JavaScript发布订阅模式:让代码沟通更优雅 在JavaScript的世界里,我们常常会遇到这样的场景:多个模块之间需要相互通信,但是又不想让它们产生过于紧密的耦合。这时候,发布订阅模式就像一位优雅的信使,…...

EC2安装WebRTC sdk-c环境、构建、编译
1、登录新的ec2实例,证书可以跟之前的实例用一个: ssh -v -i ~/Documents/cert/qa.pem ec2-user70.xxx.165.xxx 2、按照sdk-c demo中readme的描述开始安装环境: https://github.com/awslabs/amazon-kinesis-video-streams-webrtc-sdk-c 2…...
