Coin Change
一、题目
Suppose there are 5 types of coins: 50-cent, 25-cent, 10-cent, 5-cent, and 1-cent. We want to make changes with these coins for a given amount of money.
For example, if we have 11 cents, then we can make changes with one 10-cent coin and one 1-cent coin, or two 5-cent coins and one 1-cent coin, or one 5-cent coin and six 1-cent coins, or eleven 1-cent coins. So there are four ways of making changes for 11 cents with the above coins. Note that we count that there is one way of making change for zero cent.
Write a program to find the total number of different ways of making changes for any amount of money in cents. Your program should be able to handle up to 100 coins.
Input
The input file contains any number of lines, each one consisting of a number ( ≤250 ) for the amount of money in cents.
Output
For each input line, output a line containing the number of different ways of making changes with the above 5 types of coins.
Sample
Inputcopy Outputcopy
11
26
4
13
二、分析
题意要求使用五种面值的硬币,组成不同金额能有多少组合的方法
题目中有一个条件,硬币的数量不能超过100。
那么下面这种递推的方法就不能够控制硬币是数量
//错误代码
#include<iostream>
#include<cstring>
using namespace std;
const int maxn=1e3+5;
int dp[maxn];
int a[5]={1,5,10,25,50};
int main()
{int n;while(cin>>n){memset(dp,0,sizeof(dp));dp[0]=1;for(int i=0;i<5;i++)for(int j=a[i];j<=n;j++){dp[j]=dp[j]+dp[j-a[i]];}cout<<dp[n]<<endl;}
}
定义dp[i][j]表示i枚硬币组成j有的方法总数
这样就可以控制硬币的数量
//正确代码
#include <iostream>
#include <cstring>
using namespace std;
int dp[110][260];
// dp[i][j]表示i枚硬币组成j有的方法总数
int a[6] = {1, 5, 10, 25, 50};
int main()
{int n;while (cin >> n){memset(dp, 0, sizeof(dp));dp[0][0] = 1;for (int i = 0; i < 5; i++)for (int j = a[i]; j <= n; j++)for (int k = 1; k <= 100; k++){dp[k][j] += dp[k - 1][j - a[i]];}int ans = 0;for (int i = 0 ;i<= 100; i++)//要从0开始{ans += dp[i][n];}cout << ans << endl;}
}
相关文章:

Coin Change
一、题目 Suppose there are 5 types of coins: 50-cent, 25-cent, 10-cent, 5-cent, and 1-cent. We want to make changes with these coins for a given amount of money. For example, if we have 11 cents, then we can make changes with one 10-cent coin and one 1-c…...
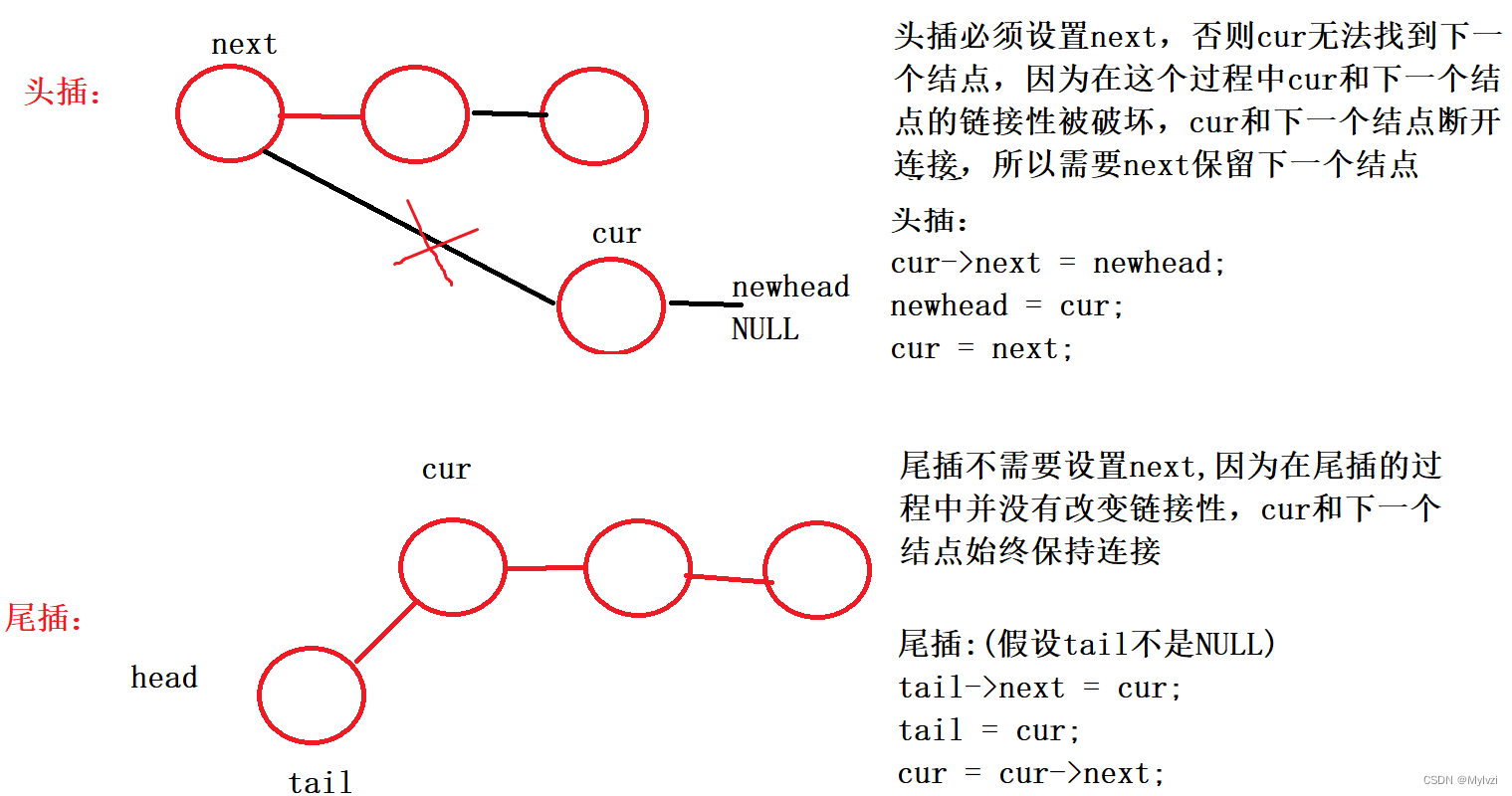
2023 8 -14链表OJ
💕人面只今何处去,桃花依旧笑春风💕 作者:Mylvzi 文章主要内容:详解链表OJ题 题目一:环形链表(判断链表是否带环) 题目描述: 画图分析: 代码实现&#x…...
大数据必回之LSM树
LSM树(Log-Structured-Merge-Tree)并不像B、红黑树一样是一颗严格的树状数据结构,它其实是一种存储结构,像HBase、RocksDB这些NoSQL存储都是采用LSM树。它是一种分层、有序、面向磁盘的数据结构,核心思想是顺序写性能远…...

Vue中的Object.defineProperty详解
Vue中的Object.defineProperty是一个比较重要的方法,它是可以定义对象中属性的一个方法,相比于在对象中直接定义的对象,它更具有灵活性。 直接定义对象中的属性是这样的: let person {name:张三,address:广东,age:12,} 而Object.…...
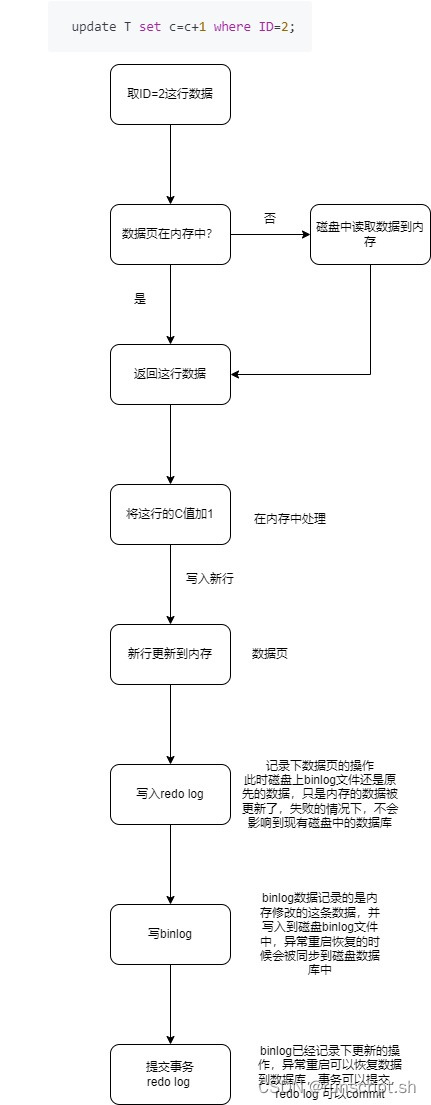
MySQL高阶知识点(一)一条SQL【更新】语句是如何执行的
一条SQL【更新】语句是如何执行的 首先,可以确定的说,【查询】语句的那一套流程,【更新】语句也是同样会走一遍,与查询流程不一样的是, 更新语句涉及到【事务】,就必须保证事务的四大特性:ACID&…...

threejs实现模型gltf的动画效果
确保加载模型后模型有animations属性。加载完模型后,在模型中定义mixer的变量值。 // 4、加入加载器 const loader new GLTFLoader(); loader.load("./model/gltf/RobotExpressive/RobotExpressive.glb", function (gltf) {// 赋值动画给mixermixer ne…...

Harmony创建项目ohpm报错
Harmony创建FA模型的项目时报如下错: The registry is empty - edit .ohpmrc file or use "ohpm config set registry your_registry" command to set registry.解决方法: File -> Settings -> Build,Execution,Deployment -> Ohpm …...

44 | 酒店预订及取消的数据分析
1.背景介绍 数据集来自Kaggle网站上公开的Hotel booking demand项目 该数据集包含了一家城市酒店和一家度假酒店的预订信息,包括预订时间、入住时间、成人、儿童或婴儿数量、可用停车位数量等信息。 数据集容量约为12万32 本次数据分析主要包含如下内容: 总览数据,完成对…...

物联网和不断发展的ITSM
物联网将改变社会,整个技术行业关于对机器连接都通过嵌入式传感器、软件和收集和交换数据的电子设备每天都在更新中。Gartner 预测,全球将有4亿台互联设备投入使用。 无论企业采用物联网的速度如何,连接设备都将成为新常态,IT服务…...

加了ComponentScan,但是feign接口无法注入的原因
正文 正确的注入 如果发现无法注入:看看启动类Application是否有加入注解:EnableFeignClients(AppConstant.BASE_PACKAGES) 注意:EnableFeignClients和ComponentScan是两个独立的扫描,所以,如果只配置了ComponentSca…...

C#Winform中DataGridView控件显示行号实例
本文演示C#Winform中如何给DataGridView控件显示行号。 首先创建winform项目,添加DataGridView控件,给控件添加两列。 修改CS代码: using System.Windows.Forms;namespace DataGridviewDemo {public partial class Form1 : Form{public Form1(){InitializeComponent();//添…...
Stable Diffusion WebUI安装和使用教程(Windows)
目录 下载Stable Diffusion WebUI运行安装程序,双击webui.bat界面启动插件安装(github)模型下载(有些需要魔法)安装过程遇到的大坑总结参考的博客 整个过程坑巨多,我花了一个晚上的时间才全部搞定,本教程针对有编程基础…...

LeetCode 35题:搜索插入位置
题目 给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。 请必须使用时间复杂度为 O(log n) 的算法。 示例 1: 输入: nums [1,3,5,6], target 5 输出: 2示例 2:…...

Linux系统中常见的几种软件包管理器
软件包管理器 DPKGAPT(APT-GET)RPMYUMDNF Linux软件包管理工具是一组命令的集合,其作用是在操作系统中提供安装、更新、删除及卸载软件的方法,同时提供对系统中所有软件状态信息的查询。不同的Linux发行版会有不同的包管理器&…...

python异步IO完全指南
原地址:https://flyingbyte.cc/post/async_io/ python异步IO完全指南 做为一种并行编程的範式,异步IO在Python中非常受重视,从Python3.4到3.7快速演进。 我们已经有多线程,多进程,并发(concurrency&#x…...

打造企业或者个人IP引流法
打造企业或者个人IP引流法. 大家好,我是百收网SEO编辑:狂潮老师,今天给大家分享企业IP打造的方法 首先我们想让人知道你的企业叫什么,怎么找到你的企业 这个时候我们就需要去各大平台发布信息,客户想了解直接去搜索…...

TMC Self-Managed 提升跨多云环境安全性
作为云原生技术栈的关键技术之一,Kubernetes 被企业用户广泛试用并开始支撑实际业务应用运行,实现技术先进性带来的生产力提升。但与此同时,随着 Kubernetes 技术的不断广泛与深化使用,企业用户也开始面临诸多技术上的挑战&#x…...
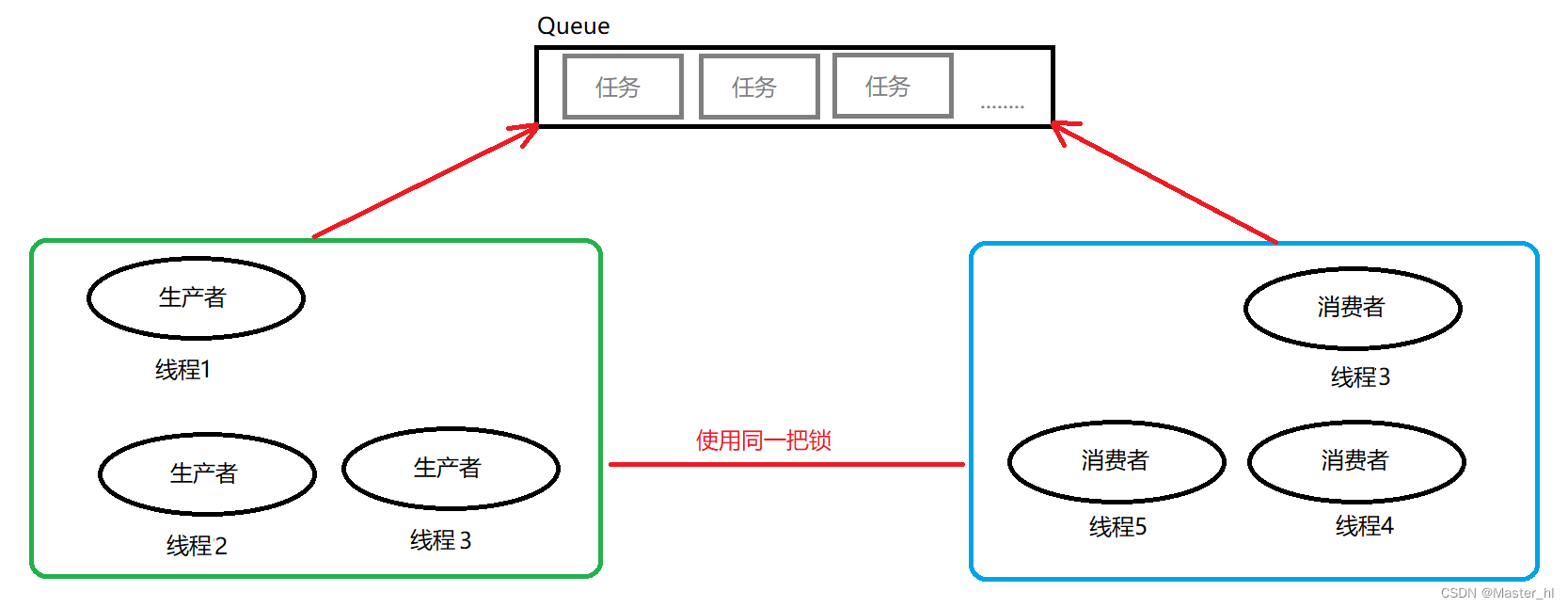
并发编程 - 线程间三种常见的通信手段
线程间通信是指多个线程之间通过某种机制进行协调和交互,例如:线程等待和通知机制就是线程通讯的主要手段之一。 在 Java 中有以下三种实现线程等待的手段 : Object 类提供的 wait(),notify() 和 notifyAll() 方法;C…...

iperf3命令使用说明
iperf3 是一款网络性能测试工具,用于在TCP和UDP数据流之间测量最大带宽。它可以帮助您测试网络连接的速度、延迟、丢包等参数。以下是一些常用的选项和参数的解释: 通用选项: -s 或 --server:运行服务器模式。-c 或 --client &l…...

华纳云:美国Linux服务器磁盘分区备份的操作方式
在美国的Linux服务器上进行磁盘分区备份可以通过以下步骤进行操作: 了解磁盘分区情况: 在开始备份之前,首先需要了解服务器上的磁盘分区情况。可以使用命令 fdisk -l 或 lsblk 查看当前的磁盘和分区信息。 安装备份工具: 如果服务…...

【网络】每天掌握一个Linux命令 - iftop
在Linux系统中,iftop是网络管理的得力助手,能实时监控网络流量、连接情况等,帮助排查网络异常。接下来从多方面详细介绍它。 目录 【网络】每天掌握一个Linux命令 - iftop工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景…...

基于大模型的 UI 自动化系统
基于大模型的 UI 自动化系统 下面是一个完整的 Python 系统,利用大模型实现智能 UI 自动化,结合计算机视觉和自然语言处理技术,实现"看屏操作"的能力。 系统架构设计 #mermaid-svg-2gn2GRvh5WCP2ktF {font-family:"trebuchet ms",verdana,arial,sans-…...

安宝特方案丨XRSOP人员作业标准化管理平台:AR智慧点检验收套件
在选煤厂、化工厂、钢铁厂等过程生产型企业,其生产设备的运行效率和非计划停机对工业制造效益有较大影响。 随着企业自动化和智能化建设的推进,需提前预防假检、错检、漏检,推动智慧生产运维系统数据的流动和现场赋能应用。同时,…...

【JVM】- 内存结构
引言 JVM:Java Virtual Machine 定义:Java虚拟机,Java二进制字节码的运行环境好处: 一次编写,到处运行自动内存管理,垃圾回收的功能数组下标越界检查(会抛异常,不会覆盖到其他代码…...

渲染学进阶内容——模型
最近在写模组的时候发现渲染器里面离不开模型的定义,在渲染的第二篇文章中简单的讲解了一下关于模型部分的内容,其实不管是方块还是方块实体,都离不开模型的内容 🧱 一、CubeListBuilder 功能解析 CubeListBuilder 是 Minecraft Java 版模型系统的核心构建器,用于动态创…...

Java - Mysql数据类型对应
Mysql数据类型java数据类型备注整型INT/INTEGERint / java.lang.Integer–BIGINTlong/java.lang.Long–––浮点型FLOATfloat/java.lang.FloatDOUBLEdouble/java.lang.Double–DECIMAL/NUMERICjava.math.BigDecimal字符串型CHARjava.lang.String固定长度字符串VARCHARjava.lang…...

跨链模式:多链互操作架构与性能扩展方案
跨链模式:多链互操作架构与性能扩展方案 ——构建下一代区块链互联网的技术基石 一、跨链架构的核心范式演进 1. 分层协议栈:模块化解耦设计 现代跨链系统采用分层协议栈实现灵活扩展(H2Cross架构): 适配层…...

Spring数据访问模块设计
前面我们已经完成了IoC和web模块的设计,聪明的码友立马就知道了,该到数据访问模块了,要不就这俩玩个6啊,查库势在必行,至此,它来了。 一、核心设计理念 1、痛点在哪 应用离不开数据(数据库、No…...

【7色560页】职场可视化逻辑图高级数据分析PPT模版
7种色调职场工作汇报PPT,橙蓝、黑红、红蓝、蓝橙灰、浅蓝、浅绿、深蓝七种色调模版 【7色560页】职场可视化逻辑图高级数据分析PPT模版:职场可视化逻辑图分析PPT模版https://pan.quark.cn/s/78aeabbd92d1...

vulnyx Blogger writeup
信息收集 arp-scan nmap 获取userFlag 上web看看 一个默认的页面,gobuster扫一下目录 可以看到扫出的目录中得到了一个有价值的目录/wordpress,说明目标所使用的cms是wordpress,访问http://192.168.43.213/wordpress/然后查看源码能看到 这…...
