Leet code1049 最后一块石头的重量II
1049 最后一块石头的重量II
【问题描述】
有一堆石头,用整数数组 stones 表示。其中 stones[i] 表示第 i 块石头的重量。
每一回合,从中选出任意两块石头,然后将它们一起粉碎。假设石头的重量分别为 x 和 y,且 x <= y。那么粉碎的可能结果如下:
- 如果
x == y,那么两块石头都会被完全粉碎; - 如果
x != y,那么重量为x的石头将会完全粉碎,而重量为y的石头新重量为y-x。
最后,最多只会剩下一块 石头。返回此石头 最小的可能重量 。如果没有石头剩下,就返回 0。
示例 1:
输入:stones = [2,7,4,1,8,1]
输出:1
解释:
组合 2 和 4,得到 2,所以数组转化为 [2,7,1,8,1],
组合 7 和 8,得到 1,所以数组转化为 [2,1,1,1],
组合 2 和 1,得到 1,所以数组转化为 [1,1,1],
组合 1 和 1,得到 0,所以数组转化为 [1],这就是最优值。
示例 2:
输入:stones = [31,26,33,21,40]
输出:5
【代码】:
class Solution {public int lastStoneWeightII(int[] stones) {int n = stones.length;int totalWeight = 0;//计算所有石头的总重量for (int stone : stones) {totalWeight += stone;}int target = totalWeight / 2;boolean[][] dp = new boolean[n][target + 1];dp[0][0] = true;if (stones[0] <= target) {dp[0][stones[0]] = true;}//状态转移for (int i = 1; i < n; i++) {for (int j = 0; j <= target; j++) {dp[i][j] = dp[i - 1][j];if (j >= stones[i]) {dp[i][j] = dp[i][j] || dp[i - 1][j - stones[i]];}}}int maxWeight = 0;for (int j = target; j >= 0; j--) {if (dp[n - 1][j]) {maxWeight = j;break;}}return totalWeight - 2 * maxWeight;}}
思路:
本题精髓就是转化为背包问题。
我们可以将石头分成两堆,假设为堆 A 和堆 B。我们的目标是使得两堆石头的重量差最小。我们可以将问题转化为在总重量不超过 totalWeight/2 的前提下,尽可能地选取石头放入堆 A。
我们定义一个二维数组 dp,其中 dp[i][j] 表示在前 i 个石头中选取一些石头,使得它们的总重量恰好为 j 是否可能。
对于每个石头 stones[i],我们有两种选择:选取它或者不选取它。如果我们选取了石头 stones[i],则有 dp[i][j] = dp[i-1][j-stones[i]],表示在前 i-1 个石头中选取一些石头,使得它们的总重量恰好为 j-stones[i] 是否可能。如果我们不选取石头 stones[i],则有 dp[i][j] = dp[i-1][j],表示在前 i-1 个石头中选取一些石头,使得它们的总重量恰好为 j 是否可能。
因此,状态转移方程为 dp[i][j] = dp[i-1][j] || dp[i-1][j-stones[i]],表示在前 i 个石头中选取一些石头,使得它们的总重量恰好为 j 是否可能。
最后,我们遍历最后一行 dp[n-1],找到最大的 j,使得 dp[n-1][j] 为 True。最后一块石头的重量为 totalWeight - 2*j。
最后,A堆的石子重量为:j。
B堆的石子重量为totalWeight - j
所以可得,abs(A-B) = totalWeight - 2 * j
而这个也正是最后无法合并,剩下的石子重量。
相关文章:

Leet code1049 最后一块石头的重量II
1049 最后一块石头的重量II 【问题描述】 有一堆石头,用整数数组 stones 表示。其中 stones[i] 表示第 i 块石头的重量。 每一回合,从中选出任意两块石头,然后将它们一起粉碎。假设石头的重量分别为 x 和 y,且 x < y。那么粉…...

Rust语法:变量,函数,控制流,struct
文章目录 变量可变与不可变变量变量与常量变量的Shadowing标量类型整数 复合类型 函数控制流if elseloop & whilefor in structstruct的定义Tuple Structstruct的方法与函数 变量 可变与不可变变量 Rust中使用let来声明变量,但是let声明的是不可变变量&#x…...

LVS简介及LVS-DR搭建
目录 一. LVS简介: 1.简介 2. LVS工作模式: 3. LVS调度算法: 4. LVS-DR集群介绍: 二.LVS-DR搭建 1.RS配置 1)两台RS,需要下载好httpd软件并准备好配置文件 2)添加虚拟IP(vip&…...

Java基础篇--日期时间类
目录 前言 Instant(时间戳)类 LocalData(日期)类 LocalTime(时间)类 LocalDataTime(日期时间)类 Duration(时间间隔)类 Period(日期间隔)类 Clock(获取时区)类 前言 在开发中经常需要处理日期和时间,Java提供…...

Vue生命周期函数 详解
以下是Vue生命周期函数的流程图和每个周期的代码详解: 流程图: beforeCreate -> created -> beforeMount -> mounted -> beforeUpdate -> updated -> beforeDestroy -> destroyed详解: beforeCreate: 触发时…...
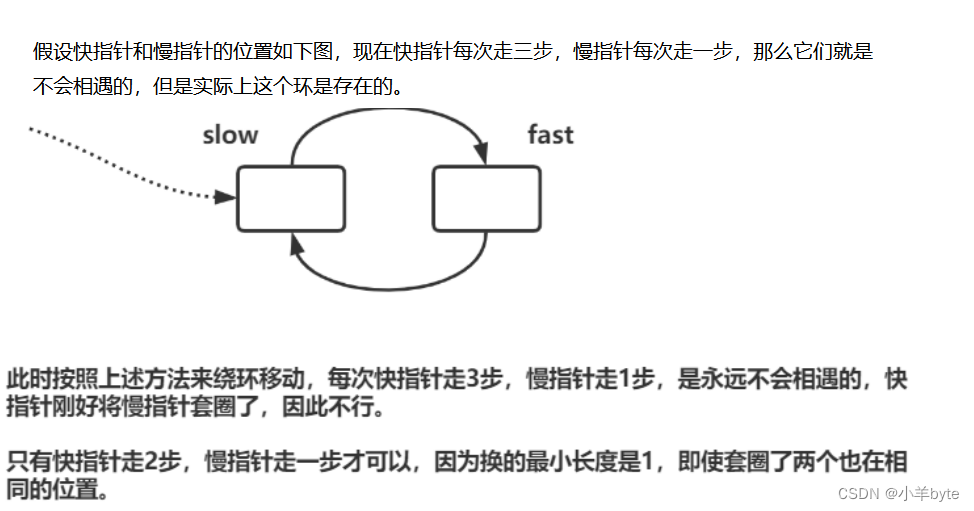
判断链表有环的证明
目录 1.问题 2.证明 3.代码实现 1.问题 给你一个链表的头节点 head ,判断链表中是否有环。 如果链表中有某个节点,可以通过连续跟踪 next 指针再次到达,则链表中存在环。 为了表示给定链表中的环,评测系统内部使用…...
百度屏蔽词有哪些?其中就有移民关键词指数被屏蔽?
我是百收网SEO,点点上面的头像,欢迎关注我哦! 今日tombkeeper消息爆料:百度指数已经屏蔽“移民”等关键词指数。 大家好,我是百收网SEO商学院的狂潮微课老师,今天我们来讲解第 12 节课关键词优化难度分析…...

代码随想录day02
977.有序数组的平方 ● 力扣题目链接 ● 给你一个按 非递减顺序 排序的整数数组 nums,返回 每个数字的平方 组成的新数组,要求也按 非递减顺序 排序。 思路 ● 暴力排序,时间复杂度O(n nlogn) ● 使用双指针,时间复杂度O(n) …...

VR时代真的到来了?
业界对苹果的期待是,打造一台真正颠覆性的,给头显设备奠定发展逻辑底座的产品,而实际上,苹果只是发布了一台更强大的头显。 大众希望苹果回答的问题是“我为什么需要一台AR或者VR产品?”,但苹果回答的是“…...

docker run 命令转化为 docker-compose 工具
工作当中需要将 docker run 转换为更方便的 docker-compose 格式,可以使用下面的工具来完成。 转换工具:https://www.composerize.com/?utm_sourceappinn.com 使用介绍:https://www.appinn.com/composerize-for-docker-compose/...
php如何对接伪原创api
在了解伪原创api的各种应用形态之后,我们继续探讨智能写作背后的核心技术。需要说明的是,智能写作和自然语言生成、自然语言理解、知识图谱、多模算法等各类人工智能算法都有紧密的关联,在百度的智能写作实践中,常根据实际需求将多…...
设计模式行为型——模板模式
目录 模板模式的定义 模板模式的实现 模板模式角色 模板模式类图 模板模式举例 模板模式代码实现 模板模式的特点 优点 缺点 使用场景 注意事项 实际应用 模板模式的定义 模板模式(Template Pattern)属于行为型设计模式,又叫模版…...

12.Eclipse导入Javaweb项目
同事复制一份他的项目给我ekp.rar (懒得从SVN上拉取代码了)放在workspace1目录下 新建一个文件夹 workspace2,Eclipse切换到workspace2工作空间 选择Import导入 选择导入的项目(这里是放到workspace1里面) 拷贝一份到workspace2里面 例子 所有不是在自己电脑上开发…...

探索自动化网页交互的魔力:学习 Selenium 之旅【超详细】
"在当今数字化的世界中,网页自动化已经成为了不可或缺的技能。想象一下,您可以通过编写代码,让浏览器自动执行各种操作,从点击按钮到填写表单,从网页抓取数据到进行自动化测试。学习 Selenium,这一功能…...

css常用样式和不常用样式
文章目录 1、hover鼠标变小手2、ul去除点3、文字溢出显示省略号(1)一行文字溢出显示省略号(2)多行文字溢出显示省略号 4、文字单词超出(1)文字单词超出换行(word-wrap)(2…...
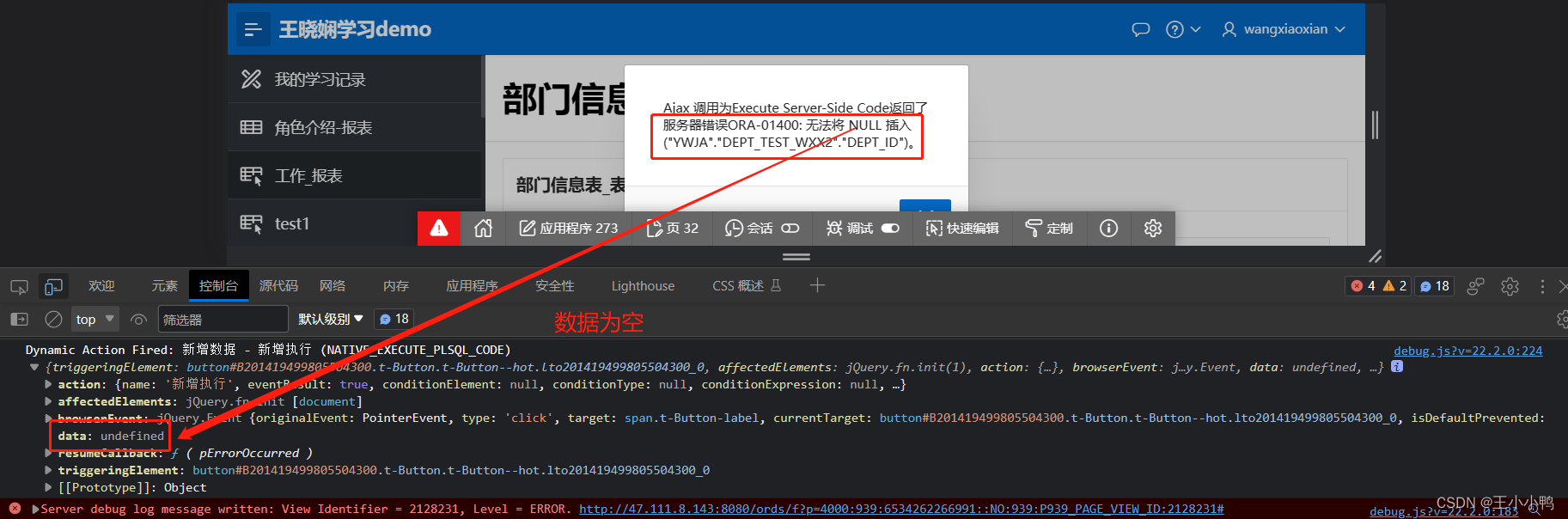
【小练习】交互式网格自定义增删改错误记录及解决(进行中)
经过之前的学习,已经能创建简单的交互式网格并设置自定义增删改按钮,但是实现上还是存在一些问题,来完善优化一下。 首先是修改,正常修改都会弹出修改框,里面是之前存储的信息,根据实际需要对其进行修改&a…...

云渲染效果不对?云渲染前的四个细节表明你的问题出在这里!
云渲染针对3D渲染行业,帮助本地电脑解决渲染慢的问题,大幅提高设计师的工作效率。但小编发现,有不少小伙伴在使用云渲染时,出现了渲染效果不对或丢失的问题,根据小伙伴们的问题和我们创意云云渲染平台给出的解决方案&a…...
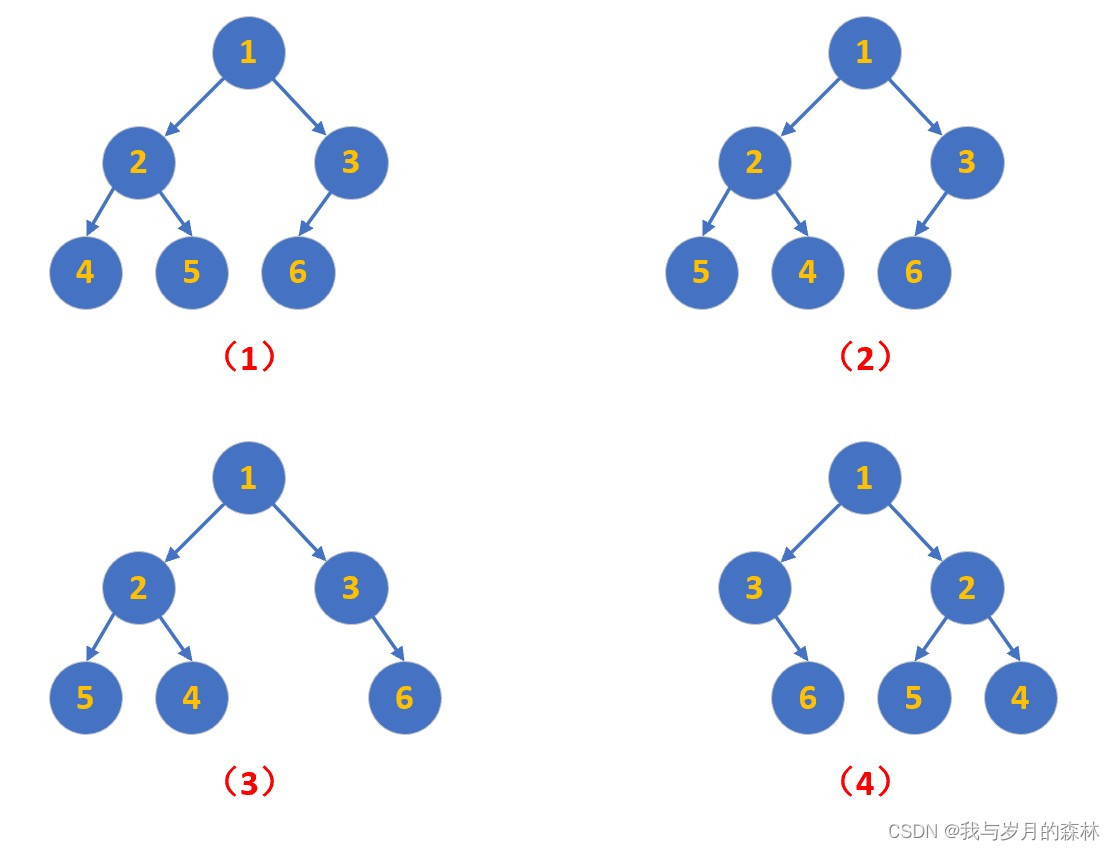
翻转二叉树
声明 该系列文章仅仅展示个人的解题思路和分析过程,并非一定是优质题解,重要的是通过分析和解决问题能让我们逐渐熟练和成长,从新手到大佬离不开一个磨练的过程,加油! 原题链接 翻转二叉树备战技术面试?…...
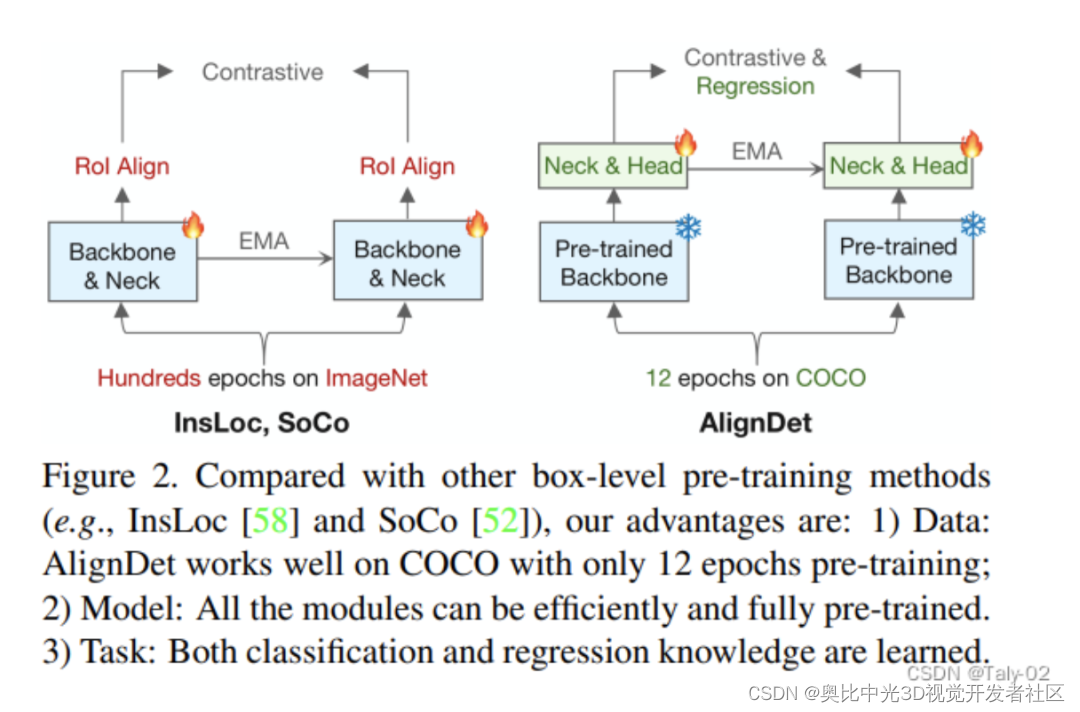
检测新突破 | AlignDet:支持各类检测器自监督新框架(ICCV2023)
引言 论文链接:https://arxiv.org/abs/2307.11077 项目地址:https://github.com/liming-ai/AlignDet 这篇论文主要研究目标检测领域的自监督预训练方法。作者首先指出,当前主流的预训练-微调框架在预训练和微调阶段存在数据、模型和任务上的…...
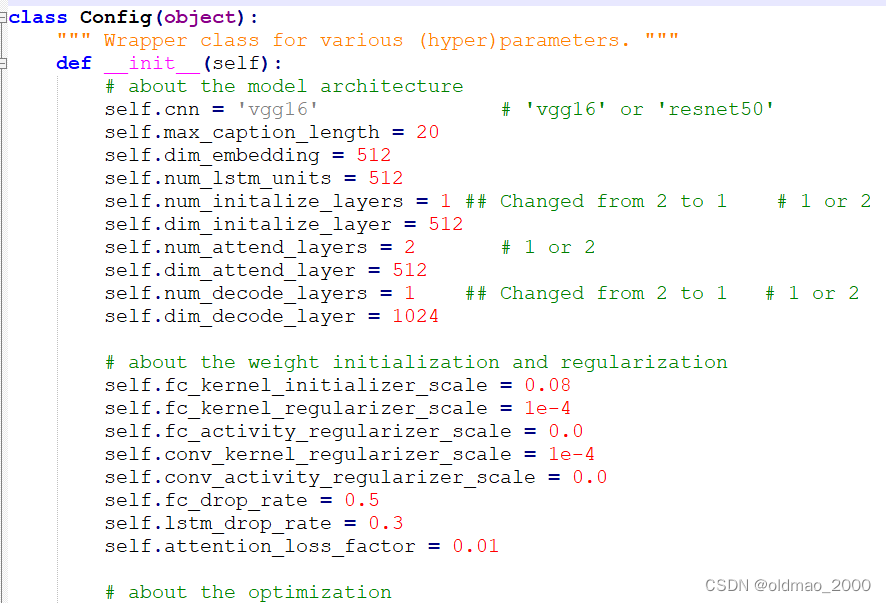
03.Show and Tell
目录 前言泛读摘要IntroductionRelated Work小结 精读模型基于LSTM的句子生成器TrainingInference 实验评价标准数据集训练细节分数结果生成结果多样性讨论排名结果人工评价结果表征分析 结论 代码 前言 本课程来自深度之眼《多模态》训练营,部分截图来自课程视频。…...

Go 语言接口详解
Go 语言接口详解 核心概念 接口定义 在 Go 语言中,接口是一种抽象类型,它定义了一组方法的集合: // 定义接口 type Shape interface {Area() float64Perimeter() float64 } 接口实现 Go 接口的实现是隐式的: // 矩形结构体…...

蓝牙 BLE 扫描面试题大全(2):进阶面试题与实战演练
前文覆盖了 BLE 扫描的基础概念与经典问题蓝牙 BLE 扫描面试题大全(1):从基础到实战的深度解析-CSDN博客,但实际面试中,企业更关注候选人对复杂场景的应对能力(如多设备并发扫描、低功耗与高发现率的平衡)和前沿技术的…...

Nuxt.js 中的路由配置详解
Nuxt.js 通过其内置的路由系统简化了应用的路由配置,使得开发者可以轻松地管理页面导航和 URL 结构。路由配置主要涉及页面组件的组织、动态路由的设置以及路由元信息的配置。 自动路由生成 Nuxt.js 会根据 pages 目录下的文件结构自动生成路由配置。每个文件都会对…...

多种风格导航菜单 HTML 实现(附源码)
下面我将为您展示 6 种不同风格的导航菜单实现,每种都包含完整 HTML、CSS 和 JavaScript 代码。 1. 简约水平导航栏 <!DOCTYPE html> <html lang"zh-CN"> <head><meta charset"UTF-8"><meta name"viewport&qu…...
)
Angular微前端架构:Module Federation + ngx-build-plus (Webpack)
以下是一个完整的 Angular 微前端示例,其中使用的是 Module Federation 和 npx-build-plus 实现了主应用(Shell)与子应用(Remote)的集成。 🛠️ 项目结构 angular-mf/ ├── shell-app/ # 主应用&…...

蓝桥杯 冶炼金属
原题目链接 🔧 冶炼金属转换率推测题解 📜 原题描述 小蓝有一个神奇的炉子用于将普通金属 O O O 冶炼成为一种特殊金属 X X X。这个炉子有一个属性叫转换率 V V V,是一个正整数,表示每 V V V 个普通金属 O O O 可以冶炼出 …...

如何配置一个sql server使得其它用户可以通过excel odbc获取数据
要让其他用户通过 Excel 使用 ODBC 连接到 SQL Server 获取数据,你需要完成以下配置步骤: ✅ 一、在 SQL Server 端配置(服务器设置) 1. 启用 TCP/IP 协议 打开 “SQL Server 配置管理器”。导航到:SQL Server 网络配…...

【安全篇】金刚不坏之身:整合 Spring Security + JWT 实现无状态认证与授权
摘要 本文是《Spring Boot 实战派》系列的第四篇。我们将直面所有 Web 应用都无法回避的核心问题:安全。文章将详细阐述认证(Authentication) 与授权(Authorization的核心概念,对比传统 Session-Cookie 与现代 JWT(JS…...

webpack面试题
面试题:webpack介绍和简单使用 一、webpack(模块化打包工具)1. webpack是把项目当作一个整体,通过给定的一个主文件,webpack将从这个主文件开始找到你项目当中的所有依赖文件,使用loaders来处理它们&#x…...

拟合问题处理
在机器学习中,核心任务通常围绕模型训练和性能提升展开,但你提到的 “优化训练数据解决过拟合” 和 “提升泛化性能解决欠拟合” 需要结合更准确的概念进行梳理。以下是对机器学习核心任务的系统复习和修正: 一、机器学习的核心任务框架 机…...
