一位心理学教师对ChatGPT的看法,提到了正确地使用它的几个要点

在没有自主学习能力和有自主学习能力的两类学生中,ChatGPT的出现,会加大他们在知识学习及思维发展上的鸿沟。爱学习的人会因为AI变得更好……
从2022年年底起,ChatGPT的技术突破使人类终于进入了一个AI被广泛应用在工作、学习、生活的时代。和以前那些所谓的AI工具不一样,这个最新的AI工具更直观、更自然、和人类的思考更接近。
我对生成式AI工具的技术突破持正面的态度,毕竟它能帮助我们处理太多太多的事情,为我们省却了很多时间。就像我一样,GPT4俨如我的良师益友,有很多东西,包括生活上的、副业上的、学术上的,我都会咨询它。[1]
除了ChatGPT外,每隔几周,各家科技公司都会犹如竞赛般新推出很多不同种类的AI工具。我们现在可以不费吹灰之力地叫AI帮我们写文案、创作图像、翻译、作曲、长文总结等等[2]。
虽然生成式AI用处广泛,但是只要细心一想,我们便会预测到将它会带来的各种问题。这这里会说下在我的专业里面(心理学教育及研究),生成式AI会带来什么影响,以及我们应该如何应用它。
生成式AI如ChatGPT会可能会致使没有自主学习能力的学生彻底放弃自主学习。一些自我驱动力差的学生,面对课业时(尤其文字式功课如写作文或读后感),会完全依赖ChatGPT的回应,不费吹灰之力就完成各种功课。在这一点上,老师的角色其实很被动,因为我们很难有100%确切的证据,来肯定学生的作业完全是抄自生成式AI。这会产生很多无谓的争吵,浪费时间。
而对于本身自我学习能力强,或是很懂得学习的同学,生成式AI绝对是他们很重要的学习伙伴,他们能更便利地从ChatGPT身上学习到很多有用的知识,并会加以验证、消化及应用。
在心理学知识传播上,笔者最担心的是ChatGPT会在网上带来更多的假心理学知识。并不是每个提问者用户都会有相关的专业知识基础,很难有能力或心思去判断ChatGPT的回应是否正确。
而由于人类懒惰的本性,会有不少人不作质疑地就将ChatGPT提供的内容发布在网上,久而久之,劣币驱逐良币,在一般的网站上,会有一大堆完全由生成式AI产出的内容,而当中错误的部分又可能会被不断重覆及传播。
我在使用ChatGPT时,发现它最容易出错的地方是参考文献——有很多的参考文献都是它瞎编出来的,所以大家使用时必须验证资料的真伪性。
要更好地运用生成式AI,将它变成自己的最强大脑,有几点我们可以谨记:
-
心态上,运用AI时,我们是主,AI是辅,我们运用AI帮助自己,但不是完全依赖AI,AI提供的文字必要经过自己审核。
-
运用ChatGPT等AI工具问某个领域的问题时,用前我们必须已拥有该领域的知识再使用适当的提示去“扩展”自己,不然我们完全无法评估ChatGPT内容产出的真实性。在没有任何知识的背景下,就去完全相信ChatGPT产出的相关内容,则是相当危险的。
-
学生写作时,可以从ChatGPT得到灵感,然后是自己起稿,再让ChatGPT为你润色文字。
参考资料
[1]https://z-p3.www.instagram.com/p/CttsaThvDsd/
[2]https://www.94c.cc/info/how-to-get-students-to-use-chatgpt-correctly-2023-7.html
相关文章:

一位心理学教师对ChatGPT的看法,提到了正确地使用它的几个要点
在没有自主学习能力和有自主学习能力的两类学生中,ChatGPT的出现,会加大他们在知识学习及思维发展上的鸿沟。爱学习的人会因为AI变得更好…… 从2022年年底起,ChatGPT的技术突破使人类终于进入了一个AI被广泛应用在工作、学习、生活的时代。…...

认识Node.js及三个模块
文章目录 1.初识 Node.js1.1 什么是 Node.js1.2 Node.js 中的 JavaScript 运行环境1.3 Node.js 可以做什么1.4 Node.js 环境的安装1.4.1 区分 LTS 版本和 Current 版本的不同1.4.2 查看已安装的 Node.js 的版本号1.4.3 什么是终端1.4.4 终端中的快捷键 1.5 在 Node.js 环境中执…...

49 | 公司销售数据分析
公司销售数据分析报告 本数据是2012~2014年间一家生产体育类产品的全球销售订单数据,分别按时间、产品类别、销售国家统计产品销售情况,分析销售额和利润额统计各产品市场占有份额,为下一步生产计划提供有价值的建议。 数据大小:88475 行, 11 列 Retailer country销售国…...
Android 项目导入高德SDK初次上手
文章目录 一、前置知识:二、学习目标三、学习资料四、操作过程1、创建空项目2、高德 SDK 环境接入2.1 获取高德 key2.2下载 SDK 并导入2.2.1、下载SDK 文件2.2.2、SDK 导入项目2.2.3、清单文件配置2.2.4、隐私权限 3、显示地图 一、前置知识: 1、Java 基…...
)
生成树协议用来解决网络风暴的问题?(第三十二课)
生成树协议用来解决网络风暴的问题?(第三十二课) 一 STP RSTP MSTP 介绍 STP(Spanning Tree Protocol)、RSTP(Rapid Spanning Tree Protocol)和MSTP(Multiple Spanning Tree Protocol)都是用于网络中避免环路的协议。 STP是最初的协议,它通过将某些端口阻塞来防止…...

git分支操作
Git分支的操作 1.1 Git分支简介 Git分支是由指针管理起来的,所以创建、切换、合并、删除分支都非常快,非常适合大型项目的开发。 在分支上做开发,调试好了后再合并到主分支。那么每个人开发模块式都不会影响到别人。 分支使用策略…...

【基础学习笔记 enum】TypeScript 中的 enum 枚举类型介绍
因为之前网上查好多博客都是只说最基础的,所以这里记录一下,最基础的放在最后面。 这里重点要记录的是枚举成员的值可以是字符串(字符串枚举,因为网上大部分只介绍常数枚举),需要注意的一点是,…...
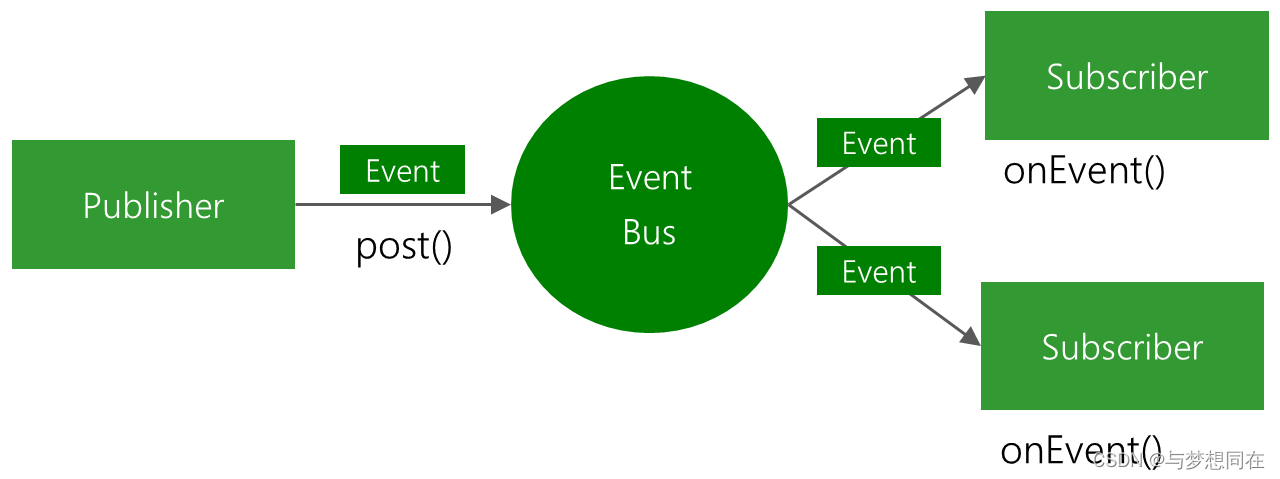
SpringBoot中间件使用之EventBus、Metric、CommandLineRunner
1、EventBus 使用EventBus 事件总线的方式可以实现消息的发布/订阅功能,EventBus是一个轻量级的消息服务组件,适用于Android和Java。 // 1.注册事件通过 EventBus.getDefault().register(); // 2.发布事件 EventBus.getDefault().post(“事件内容”); …...

ffmpeg命令行是如何打开vf_scale滤镜的
前言 在ffmpeg命令行中,ffmpeg -i test -pix_fmt rgb24 test.rgb,会自动打开ff_vf_scale滤镜,本章主要追踪这个流程。 通过gdb可以发现其基本调用栈如下: 可以看到,query_formats()中创建的v…...
【Vue3】自动引入插件-`unplugin-auto-import`
Vue3自动引入插件-unplugin-auto-import,不必再手动 import 。 自动导入 api 按需为 Vite, Webpack, Rspack, Rollup 和 esbuild 。支持TypeScript。由unplugin驱动。 插件安装:unplugin-auto-import 配置vite.config.ts(配置完后需要重启…...

每日温度(力扣)单调栈 JAVA
给定一个整数数组 temperatures ,表示每天的温度,返回一个数组 answer ,其中 answer[i] 是指对于第 i 天,下一个更高温度出现在几天后。如果气温在这之后都不会升高,请在该位置用 0 来代替。 示例 1: 输入: temperatur…...
博客项目(Spring Boot)
1.需求分析 注册功能(添加用户操纵)登录功能(查询操作)我的文章列表页(查询我的文章|文章修改|文章详情|文章删除)博客编辑页(添加文章操作)所有人博客列表(带分页功能)…...

修改Jenkins存储目录
注意:在Jenkins运行时是不能更改的. 请先将Jenkins停止运行。 1、windows环境下更改JENKINS的主目录 Windows环境中,Jenkins主目录默认在C:Documents and SettingsAAA.jenkins 。可以通过设置环境变量来修改,例如: JENKINS_HOME…...
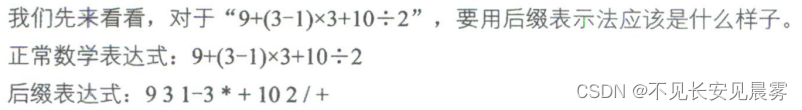
数据结构【第4章】——栈与队列
队列是只允许在一端进行插入操作、而在另-端进行删除操作的线性表。 栈 栈与队列:栈是限定仅在表尾进行插入和删除操作的线性表。 我们把允许插入和删除的一端称为栈顶(top),另一端称为栈底(bottom)&…...

android webview 显示灰度网页
要在WebView中显示网页灰度显示,您可以通过以下步骤操作: 在您的布局文件中添加WebView组件: <WebViewandroid:id"id/webview"android:layout_width"match_parent"android:layout_height"match_parent" /…...
)
Linux操作系统的基础使用技能的训练大纲(超级详细版本适合于初学者)
RHCE红帽认证工程师课程对应考试课 程 纲 要 第一部分 网络基础 RH033RH302 Linux基础: 1) 在bashshell命令行模式下运行基本的Linux命令 2) 从命令行及GNOME界面启动应用程序 3) 使用及配置Xwindow系统及GNOME桌面环境 4) 使用GNOME GUI应用程序完成一般的工作 5) 了解Linu…...

【变形金刚02】注意机制以及BERT 和 GPT
一、说明 我已经解释了什么是注意力机制,以及与转换器相关的一些重要关键字和块,例如自我注意、查询、键和值以及多头注意力。在这一部分中,我将解释这些注意力块如何帮助创建转换器网络,注意、自我注意、多头注意、蒙面多头注意力…...
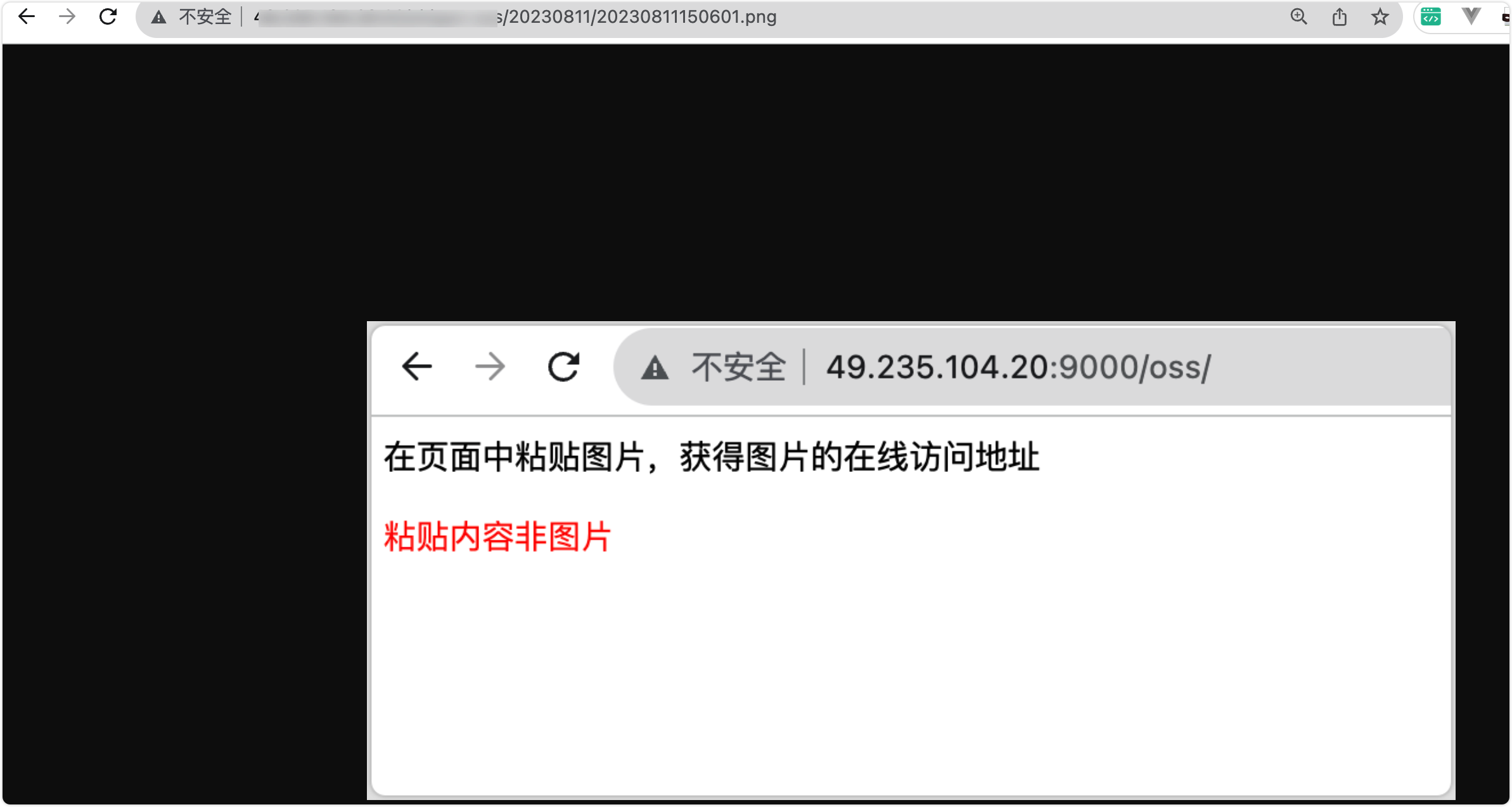
一个脚本 专治杂乱
背景 之前不是自己手动搞了一个COS嘛,直接复制粘贴图片,上传到后端的服务器,返回一个可访问的地址。我在哔哩哔哩上也分享过这样的一期视频。 今天偶尔上服务器一看,我靠,我的文件真的乱! 这还得了了&…...
springboot 基础
巩固基础,砥砺前行 。 只有不断重复,才能做到超越自己。 能坚持把简单的事情做到极致,也是不容易的。 SpringBoot JavaEE 简介 JavaEE的局限性: 1、过于复杂,JavaEE正对的是复杂的分布式企业应用,然而现实…...

web集群学习:基于nginx的反向代理和负载均衡
目录 一,反向代理 1,环境准备 2,配置代理服务器 3,在物理机上一管理员身份打开文本编辑器,编辑C:\Windows\System32\drivers\etc目录下的hosts文件 4,访问测试 5,查看日志,并记…...
:OpenBCI_GUI:从环境搭建到数据可视化(下))
脑机新手指南(八):OpenBCI_GUI:从环境搭建到数据可视化(下)
一、数据处理与分析实战 (一)实时滤波与参数调整 基础滤波操作 60Hz 工频滤波:勾选界面右侧 “60Hz” 复选框,可有效抑制电网干扰(适用于北美地区,欧洲用户可调整为 50Hz)。 平滑处理&…...

如何将联系人从 iPhone 转移到 Android
从 iPhone 换到 Android 手机时,你可能需要保留重要的数据,例如通讯录。好在,将通讯录从 iPhone 转移到 Android 手机非常简单,你可以从本文中学习 6 种可靠的方法,确保随时保持连接,不错过任何信息。 第 1…...

Robots.txt 文件
什么是robots.txt? robots.txt 是一个位于网站根目录下的文本文件(如:https://example.com/robots.txt),它用于指导网络爬虫(如搜索引擎的蜘蛛程序)如何抓取该网站的内容。这个文件遵循 Robots…...

【决胜公务员考试】求职OMG——见面课测验1
2025最新版!!!6.8截至答题,大家注意呀! 博主码字不易点个关注吧,祝期末顺利~~ 1.单选题(2分) 下列说法错误的是:( B ) A.选调生属于公务员系统 B.公务员属于事业编 C.选调生有基层锻炼的要求 D…...

MySQL 8.0 OCP 英文题库解析(十三)
Oracle 为庆祝 MySQL 30 周年,截止到 2025.07.31 之前。所有人均可以免费考取原价245美元的MySQL OCP 认证。 从今天开始,将英文题库免费公布出来,并进行解析,帮助大家在一个月之内轻松通过OCP认证。 本期公布试题111~120 试题1…...

JUC笔记(上)-复习 涉及死锁 volatile synchronized CAS 原子操作
一、上下文切换 即使单核CPU也可以进行多线程执行代码,CPU会给每个线程分配CPU时间片来实现这个机制。时间片非常短,所以CPU会不断地切换线程执行,从而让我们感觉多个线程是同时执行的。时间片一般是十几毫秒(ms)。通过时间片分配算法执行。…...

如何在网页里填写 PDF 表格?
有时候,你可能希望用户能在你的网站上填写 PDF 表单。然而,这件事并不简单,因为 PDF 并不是一种原生的网页格式。虽然浏览器可以显示 PDF 文件,但原生并不支持编辑或填写它们。更糟的是,如果你想收集表单数据ÿ…...

MacOS下Homebrew国内镜像加速指南(2025最新国内镜像加速)
macos brew国内镜像加速方法 brew install 加速formula.jws.json下载慢加速 🍺 最新版brew安装慢到怀疑人生?别怕,教你轻松起飞! 最近Homebrew更新至最新版,每次执行 brew 命令时都会自动从官方地址 https://formulae.…...

关于uniapp展示PDF的解决方案
在 UniApp 的 H5 环境中使用 pdf-vue3 组件可以实现完整的 PDF 预览功能。以下是详细实现步骤和注意事项: 一、安装依赖 安装 pdf-vue3 和 PDF.js 核心库: npm install pdf-vue3 pdfjs-dist二、基本使用示例 <template><view class"con…...

「全栈技术解析」推客小程序系统开发:从架构设计到裂变增长的完整解决方案
在移动互联网营销竞争白热化的当下,推客小程序系统凭借其裂变传播、精准营销等特性,成为企业抢占市场的利器。本文将深度解析推客小程序系统开发的核心技术与实现路径,助力开发者打造具有市场竞争力的营销工具。 一、系统核心功能架构&…...
