用javascript分类刷leetcode17.栈(图文视频讲解)
目录
-
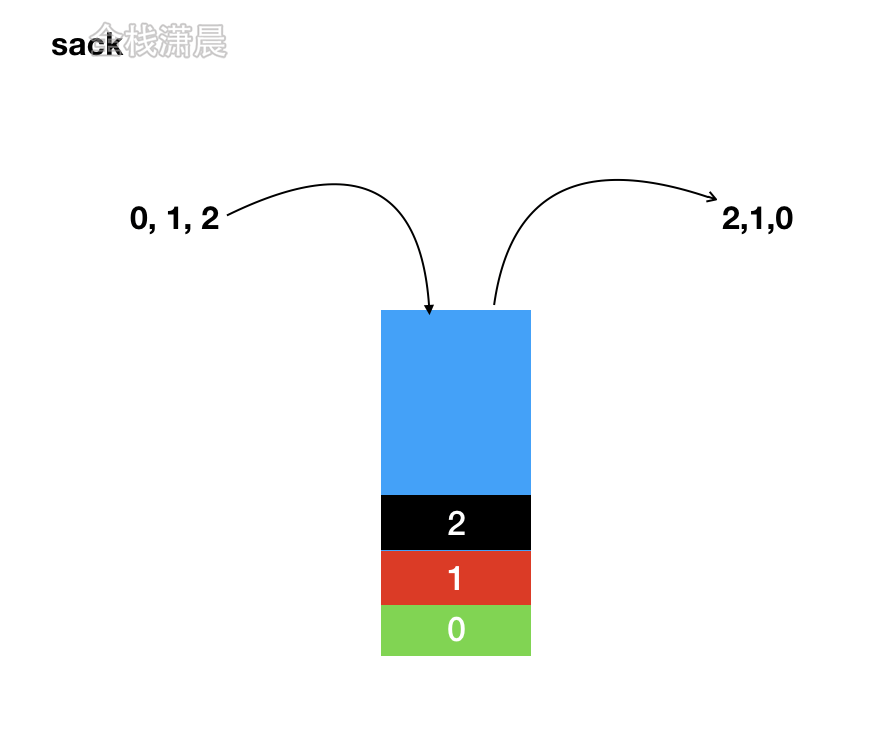
Stack的特点:先进后出(FILO)
-
使用场景:十进制转2进制 函数调用堆栈
-
js里没有栈,但是可以用数组模拟
42/2 42%2=0 21/2 21%2=1 10/2 10%2=0 5/2 5%2=1 2/2 2%2=0 1/2 1%2=1 stack: [0,1,0,1,0,1] res: 1 0 1 0 1 0fn1(){fn2() } fn2(){fn3()} fn3(){} fn1()stack:[fn1,fn2,fn3] -
栈的时间复杂度:入栈和出栈
O(1),查找O(n)
155. 最小栈 (easy)
设计一个支持 push ,pop ,top 操作,并能在常数时间内检索到最小元素的栈。
实现 MinStack 类:
MinStack() 初始化堆栈对象。
void push(int val) 将元素val推入堆栈。
void pop() 删除堆栈顶部的元素。
int top() 获取堆栈顶部的元素。
int getMin() 获取堆栈中的最小元素。示例 1:
输入:
[“MinStack”,“push”,“push”,“push”,“getMin”,“pop”,“top”,“getMin”]
[[],[-2],[0],[-3],[],[],[],[]]输出:
[null,null,null,null,-3,null,0,-2]解释:
MinStack minStack = new MinStack();
minStack.push(-2);
minStack.push(0);
minStack.push(-3);
minStack.getMin(); --> 返回 -3.
minStack.pop();
minStack.top(); --> 返回 0.
minStack.getMin(); --> 返回 -2.提示:
-231 <= val <= 231 - 1
pop、top 和 getMin 操作总是在 非空栈 上调用
push, pop, top, and getMin最多被调用 3 * 104 次
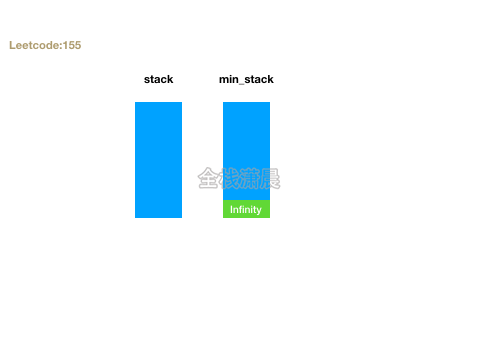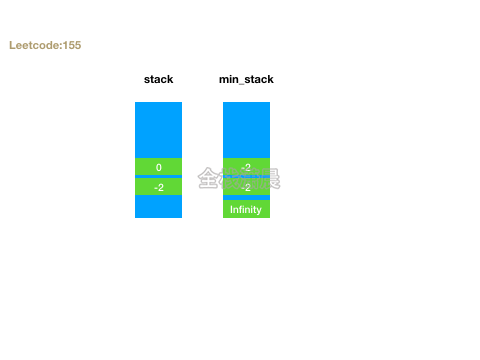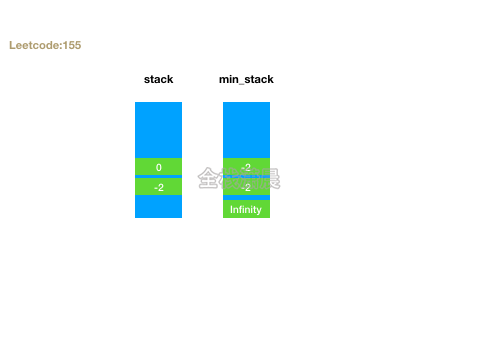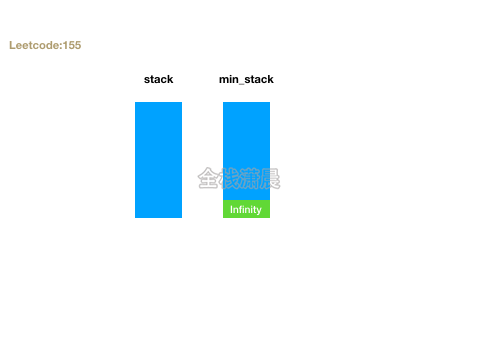
- 思路:定义两个栈stack和min_stack,stack正常push,min_stack只会push需要入栈和栈顶中较小的元素。getMin返回min_stack栈顶元素,top返回stack栈顶元素。
- 复杂度:所有操作的时间复杂度是
O(1)
js:
var MinStack = function () {this.stack = [];this.min_stack = [Infinity];
};//stack正常push,min_stack只会push需要入栈和栈顶中较小的元素
MinStack.prototype.push = function (x) {this.stack.push(x);this.min_stack.push(Math.min(this.min_stack[this.min_stack.length - 1], x));
};//stack正常pop,min_stack正常pop
MinStack.prototype.pop = function () {this.stack.pop();this.min_stack.pop();
};//返回stack栈顶元素
MinStack.prototype.top = function () {return this.stack[this.stack.length - 1];
};//返回min_stack栈顶元素
MinStack.prototype.getMin = function () {return this.min_stack[this.min_stack.length - 1];
};
946. 验证栈序列 (medium)
给定 pushed 和 popped 两个序列,每个序列中的 值都不重复,只有当它们可能是在最初空栈上进行的推入 push 和弹出 pop 操作序列的结果时,返回 true;否则,返回 false 。
示例 1:
输入:pushed = [1,2,3,4,5], popped = [4,5,3,2,1]
输出:true
解释:我们可以按以下顺序执行:
push(1), push(2), push(3), push(4), pop() -> 4,
push(5), pop() -> 5, pop() -> 3, pop() -> 2, pop() -> 1
示例 2:输入:pushed = [1,2,3,4,5], popped = [4,3,5,1,2]
输出:false
解释:1 不能在 2 之前弹出。提示:
1 <= pushed.length <= 1000
0 <= pushed[i] <= 1000
pushed 的所有元素 互不相同
popped.length == pushed.length
popped 是 pushed 的一个排列
动画过大,点击查看
- 思路:用栈模拟出栈入栈的过程,当popped中index指向的位置的元素和stack栈顶的元素一致时,出栈 并且
index++,最后判断stack是否为空 - 复杂度:时间复杂度
O(n),pushed中的元素入栈出栈一次,空间复杂度O(n),栈的大小
js:
const validateStackSequences = (pushed, popped) => {const stack = [];//用栈模拟出栈入栈的过程let index = 0;const len = pushed.length;for (let i = 0; i < len; i++) {stack.push(pushed[i]);//当popped中index指向的位置的元素和stack栈顶的元素一致时,出栈 并且 index++while (popped[index] !== undefined && popped[index] === stack[stack.length - 1]) {stack.pop();index++;}}return !stack.length;//最后判断stack是否为空
};
232. 用栈实现队列 (easy)
请你仅使用两个栈实现先入先出队列。队列应当支持一般队列支持的所有操作(push、pop、peek、empty):
实现 MyQueue 类:
void push(int x) 将元素 x 推到队列的末尾
int pop() 从队列的开头移除并返回元素
int peek() 返回队列开头的元素
boolean empty() 如果队列为空,返回 true ;否则,返回 false
说明:你 只能 使用标准的栈操作 —— 也就是只有 push to top, peek/pop from top, size, 和 is empty 操作是合法的。
你所使用的语言也许不支持栈。你可以使用 list 或者 deque(双端队列)来模拟一个栈,只要是标准的栈操作即可。示例 1:
输入:
[“MyQueue”, “push”, “push”, “peek”, “pop”, “empty”]
[[], [1], [2], [], [], []]
输出:
[null, null, null, 1, 1, false]解释:
MyQueue myQueue = new MyQueue();
myQueue.push(1); // queue is: [1]
myQueue.push(2); // queue is: [1, 2] (leftmost is front of the queue)
myQueue.peek(); // return 1
myQueue.pop(); // return 1, queue is [2]
myQueue.empty(); // return false提示:
1 <= x <= 9
最多调用 100 次 push、pop、peek 和 empty
假设所有操作都是有效的 (例如,一个空的队列不会调用 pop 或者 peek 操作)进阶:
你能否实现每个操作均摊时间复杂度为 O(1) 的队列?换句话说,执行 n 个操作的总时间复杂度为 O(n) ,即使其中一个操作可能花费较长时间。
方法1.栈
动画过大,点击查看
- 思路:这是一道模拟题,不涉及到具体算法,考察的就是对栈和队列的掌握程度。使用栈来模式队列的行为,如果仅仅用一个栈,是一定不行的,所以需要两个栈一个输入栈,一个输出栈,这里要注意输入栈和输出栈的关系。在push数据的时候,只要数据放进输入栈就好,但在pop的时候,操作就复杂一些,输出栈如果为空,就把进栈数据全部导入进来(注意是全部导入),再从出栈弹出数据,如果输出栈不为空,则直接从出栈弹出数据就可以了。最后如果进栈和出栈都为空的话,说明模拟的队列为空了。
- 复杂度分析:push时间复杂度
O(1),pop时间复杂度为O(n),因为pop的时候,输出栈为空,则把输入栈所有的元素加入输出栈。空间复杂度O(n),两个栈空间
js:
var MyQueue = function() {//准备两个栈this.stack1 = [];this.stack2 = [];
};MyQueue.prototype.push = function(x) {//push的时候加入输入栈this.stack1.push(x);
};MyQueue.prototype.pop = function() {const size = this.stack2.length;if(size) {//push的时候判断输出栈是否为空return this.stack2.pop();//不为空则输出栈出栈}while(this.stack1.length) {//输出栈为空,则把输入栈所有的元素加入输出栈this.stack2.push(this.stack1.pop());}return this.stack2.pop();
};MyQueue.prototype.peek = function() {const x = this.pop();//查看队头的元素 复用pop方法,然后在让元素push进输出栈this.stack2.push(x);return x;
};MyQueue.prototype.empty = function() {return !this.stack1.length && !this.stack2.length
};
20. 有效的括号 (easy)
给定一个只包括 ‘(’,‘)’,‘{’,‘}’,‘[’,‘]’ 的字符串 s ,判断字符串是否有效。
有效字符串需满足:
左括号必须用相同类型的右括号闭合。
左括号必须以正确的顺序闭合。
每个右括号都有一个对应的相同类型的左括号。示例 1:
输入:s = “()”
输出:true
示例 2:输入:s = “()[]{}”
输出:true
示例 3:输入:s = “(]”
输出:false提示:
1 <= s.length <= 104
s 仅由括号 ‘()[]{}’ 组成
方法1.栈
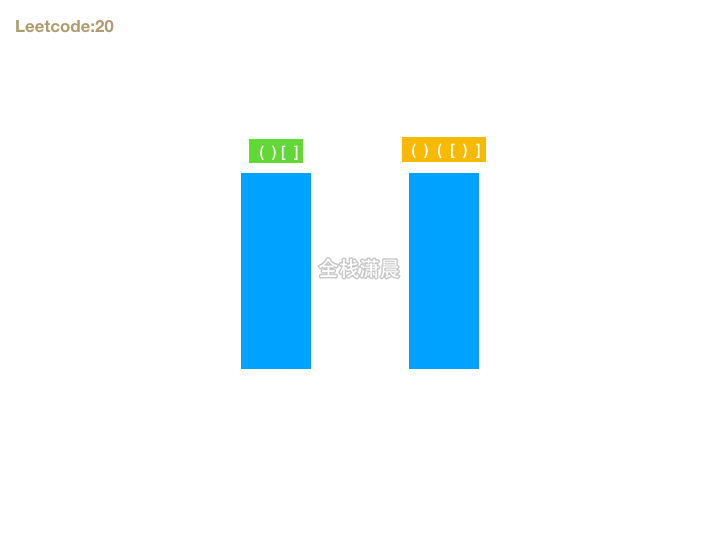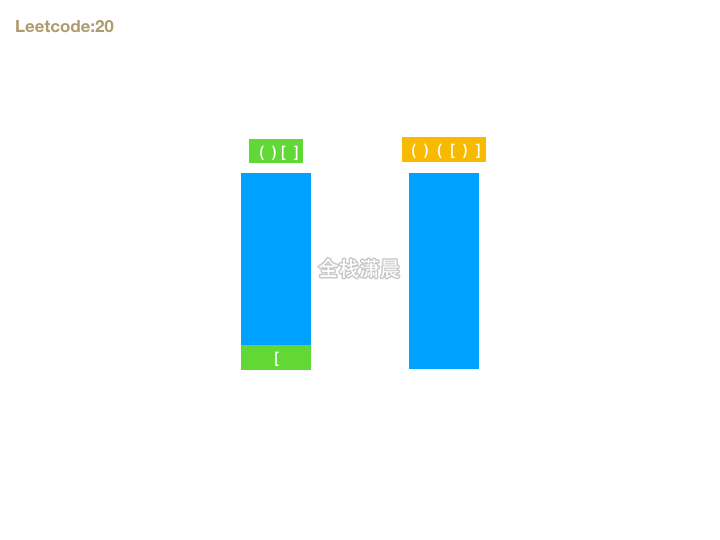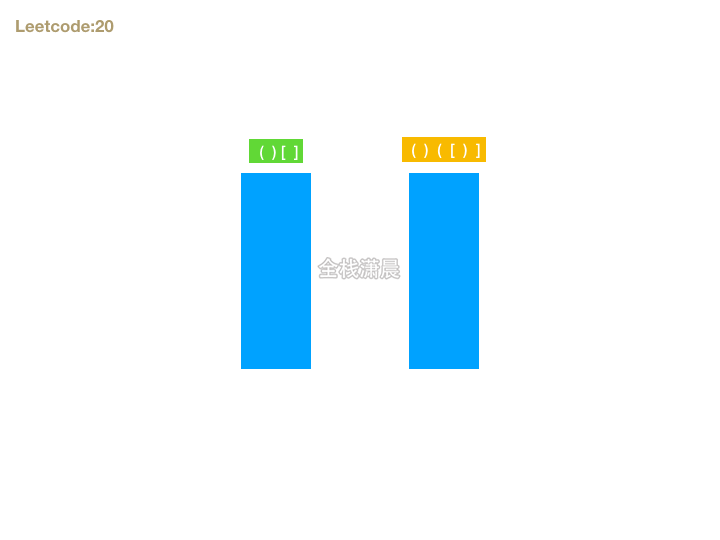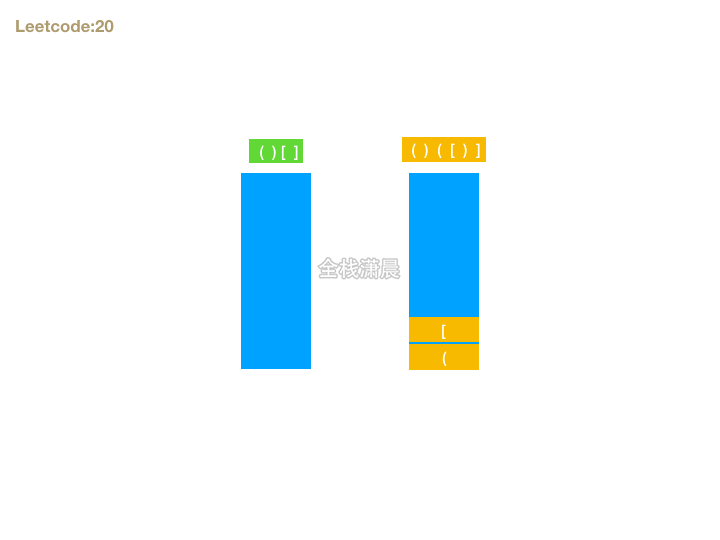
- 思路:首先如果字符串能组成有效的括号,则长度一定是偶数,我们可以遍历字符串,遇到左括号则暂存,期待后面有右括号可以和它匹配,如果遇到右括号则检查是否能和最晚暂存的做括号匹配。这就和栈这种数据结构先进后出的特性相吻合了。所以我们可以准备一个栈存放括号对,遍历字符串的时候,如果遇到左括号入栈,遇到右括号则判断右括号是否能和栈顶元素匹配,在循环结束的时候还要判断栈是否为空,如果不为空,则不是有效括号匹配的字符串
- 复杂度分析:时间复杂度
O(n),空间复杂度O(n),n为字符串的长度
js:
var isValid = function(s) {const n = s.length;if (n % 2 === 1) {//如果字符串能组成有效的括号,则长度一定是偶数return false;}const pairs = new Map([//用栈存储括号对[')', '('],[']', '['],['}', '{']]);const stk = [];for (let ch of s){//循环字符串if (pairs.has(ch)) {//遇到右括号则判断右括号是否能和栈顶元素匹配if (!stk.length || stk[stk.length - 1] !== pairs.get(ch)) {return false;}stk.pop();} else {stk.push(ch);//如果遇到左括号入栈}};return !stk.length;//循环结束的时候还要判断栈是否为空
};
445. 两数相加 II (medium)
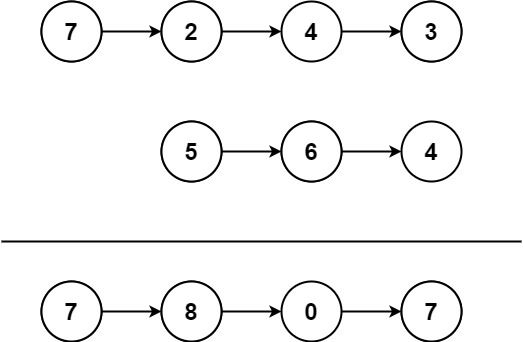
给你两个 非空 链表来代表两个非负整数。数字最高位位于链表开始位置。它们的每个节点只存储一位数字。将这两数相加会返回一个新的链表。
你可以假设除了数字 0 之外,这两个数字都不会以零开头。
示例1:
输入:l1 = [7,2,4,3], l2 = [5,6,4]
输出:[7,8,0,7]
示例2:输入:l1 = [2,4,3], l2 = [5,6,4]
输出:[8,0,7]
示例3:输入:l1 = [0], l2 = [0]
输出:[0]提示:
链表的长度范围为 [1, 100]
0 <= node.val <= 9
输入数据保证链表代表的数字无前导 0进阶:如果输入链表不能翻转该如何解决?
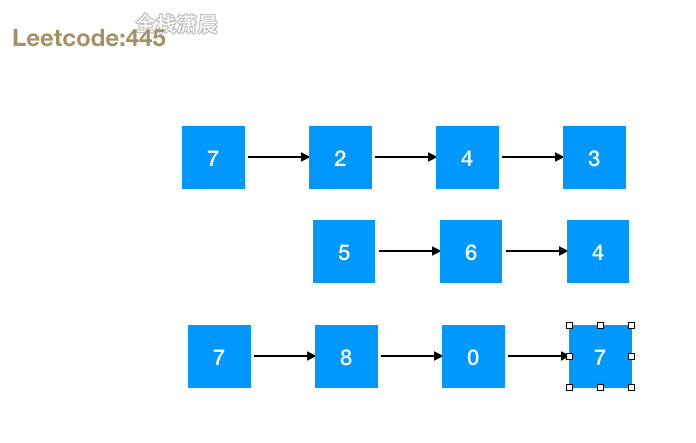
- 思路:将两个链表的节点都推入栈中,然后不断出栈,计算每个位置的值和进位,串连成一个新的链表
- 复杂度:时间复杂度
O(max(m,n)),m,n是两个链表的长度,空间复杂度O(m+n)
js:
var addTwoNumbers = function(l1, l2) {const stack1 = [];const stack2 = [];while (l1 || l2) {//两链表入栈if (l1) {stack1.push(l1.val);l1 = l1.next;}if (l2) {stack2.push(l2.val);l2 = l2.next;}}let carry = 0;let ansList = null;while (stack1.length || stack2.length || carry !== 0) {//不断出栈const s1 = stack1.length ? stack1.pop() : 0;const s2 = stack2.length ? stack2.pop() : 0;let val = s1 + s2 + carry;carry = parseInt(val / 10);//计算进位val = val % 10;//计算当前节点的值const curNode = new ListNode(val);curNode.next = ansList;//向链表前插入新节点ansList = curNode;//重新赋值ansList}return ansList;
};
682. 棒球比赛 (easy)
你现在是一场采用特殊赛制棒球比赛的记录员。这场比赛由若干回合组成,过去几回合的得分可能会影响以后几回合的得分。
比赛开始时,记录是空白的。你会得到一个记录操作的字符串列表 ops,其中 ops[i] 是你需要记录的第 i 项操作,ops 遵循下述规则:
整数 x - 表示本回合新获得分数 x
“+” - 表示本回合新获得的得分是前两次得分的总和。题目数据保证记录此操作时前面总是存在两个有效的分数。
“D” - 表示本回合新获得的得分是前一次得分的两倍。题目数据保证记录此操作时前面总是存在一个有效的分数。
“C” - 表示前一次得分无效,将其从记录中移除。题目数据保证记录此操作时前面总是存在一个有效的分数。
请你返回记录中所有得分的总和。示例 1:
输入:ops = [“5”,“2”,“C”,“D”,“+”]
输出:30
解释:
“5” - 记录加 5 ,记录现在是 [5]
“2” - 记录加 2 ,记录现在是 [5, 2]
“C” - 使前一次得分的记录无效并将其移除,记录现在是 [5].
“D” - 记录加 2 * 5 = 10 ,记录现在是 [5, 10].
“+” - 记录加 5 + 10 = 15 ,记录现在是 [5, 10, 15].
所有得分的总和 5 + 10 + 15 = 30
示例 2:输入:ops = [“5”,“-2”,“4”,“C”,“D”,“9”,“+”,“+”]
输出:27
解释:
“5” - 记录加 5 ,记录现在是 [5]
“-2” - 记录加 -2 ,记录现在是 [5, -2]
“4” - 记录加 4 ,记录现在是 [5, -2, 4]
“C” - 使前一次得分的记录无效并将其移除,记录现在是 [5, -2]
“D” - 记录加 2 * -2 = -4 ,记录现在是 [5, -2, -4]
“9” - 记录加 9 ,记录现在是 [5, -2, -4, 9]
“+” - 记录加 -4 + 9 = 5 ,记录现在是 [5, -2, -4, 9, 5]
“+” - 记录加 9 + 5 = 14 ,记录现在是 [5, -2, -4, 9, 5, 14]
所有得分的总和 5 + -2 + -4 + 9 + 5 + 14 = 27
示例 3:输入:ops = [“1”]
输出:1提示:
1 <= ops.length <= 1000
ops[i] 为 “C”、“D”、“+”,或者一个表示整数的字符串。整数范围是 [-3 * 104, 3 * 104]
对于 “+” 操作,题目数据保证记录此操作时前面总是存在两个有效的分数
对于 “C” 和 “D” 操作,题目数据保证记录此操作时前面总是存在一个有效的分数
- 复杂度:时间复杂度
O(n),空间复杂度O(n)
js:
let calPoints = function(ops) {let res = [];for(let i = 0; i < ops.length; i++){switch(ops[i]){case "C":res.pop();break;case "D":res.push(+res[res.length - 1] * 2);break;case "+":res.push(+res[res.length - 1] + +res[res.length - 2]);break;default:res.push(+ops[i]);}}return res.reduce((i, j) => i + j, 0);
};
视频讲解:传送门
相关文章:

用javascript分类刷leetcode17.栈(图文视频讲解)
目录 Stack的特点:先进后出(FILO) 使用场景:十进制转2进制 函数调用堆栈 js里没有栈,但是可以用数组模拟 42/2 42%20 21/2 21%21 10/2 10%20 5/2 5%21 2/2 2%20 1/2 1%21 stack: [0,1,0,1,0,1] res: 1 0 1 …...

转换大小写与完成字符串反转
问题 编写一个程序,实现字符串的大小写转换并倒序输出,如输入为“HelloWord”,输出为“DROwOLLEH”。 方法 需要掌握char与int的转换,需要将helloord大写输出和W小写输出,不能直接使用toUpperCase方法。因此可以使用ch…...

大数据框架之Hadoop:MapReduce(三)MapReduce框架原理——InputFormat数据输入
3.1.1切片与MapTask并行度决定机制 1、问题引出 MapTask的并行度决定Map阶段的任务处理并发度,进而影响到整个Job的处理速度。 思考:1G的数据,启动8个MapTask,可以提高集群的并发处理能力。那么1K的数据,也启动8个M…...
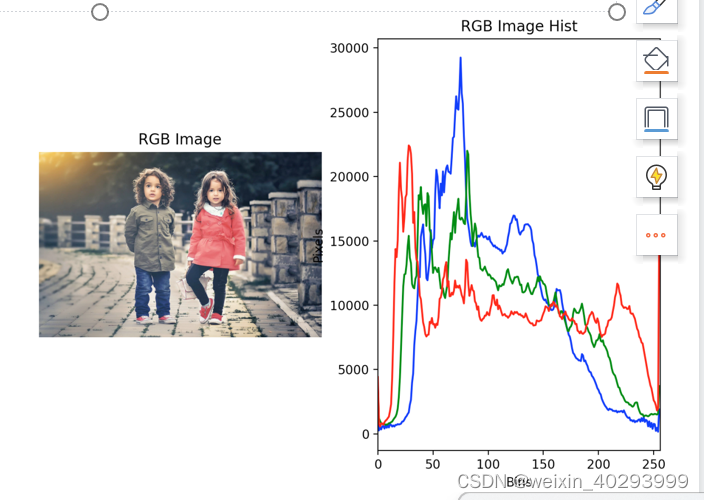
【Opencv 系列】 第4章 直方图
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录前言1、直方图的定义、意义、特征2、直方图:2.1 灰度直方图2.2 彩色直方图前言 提示:以下是本篇文章正文内容,下面案例可供参考 …...
C#反射原理
一、前言反射(Reflection)的内容在博客中已经写了一篇,什么是反射,反射的使用,反射优缺点总结;在面试中突然被问道反射的原理,按照理解反射就是在Reflection命名空间和对象的Type对象获取类的方…...
python+vue微信小程序的线上服装店系统
服装行业是一个传统的行业。根据当前发展现状,网络信息时代的全面普及,服装行业也在发生着变化,单就服饰这一方面,利用手机购物正在逐步进入人们的生活。传统的购物方式,不仅会耗费大量的人力、时间,有时候还会出错。小程序系统伴随智能手机为我们提供了新的方向。手机线上服装…...
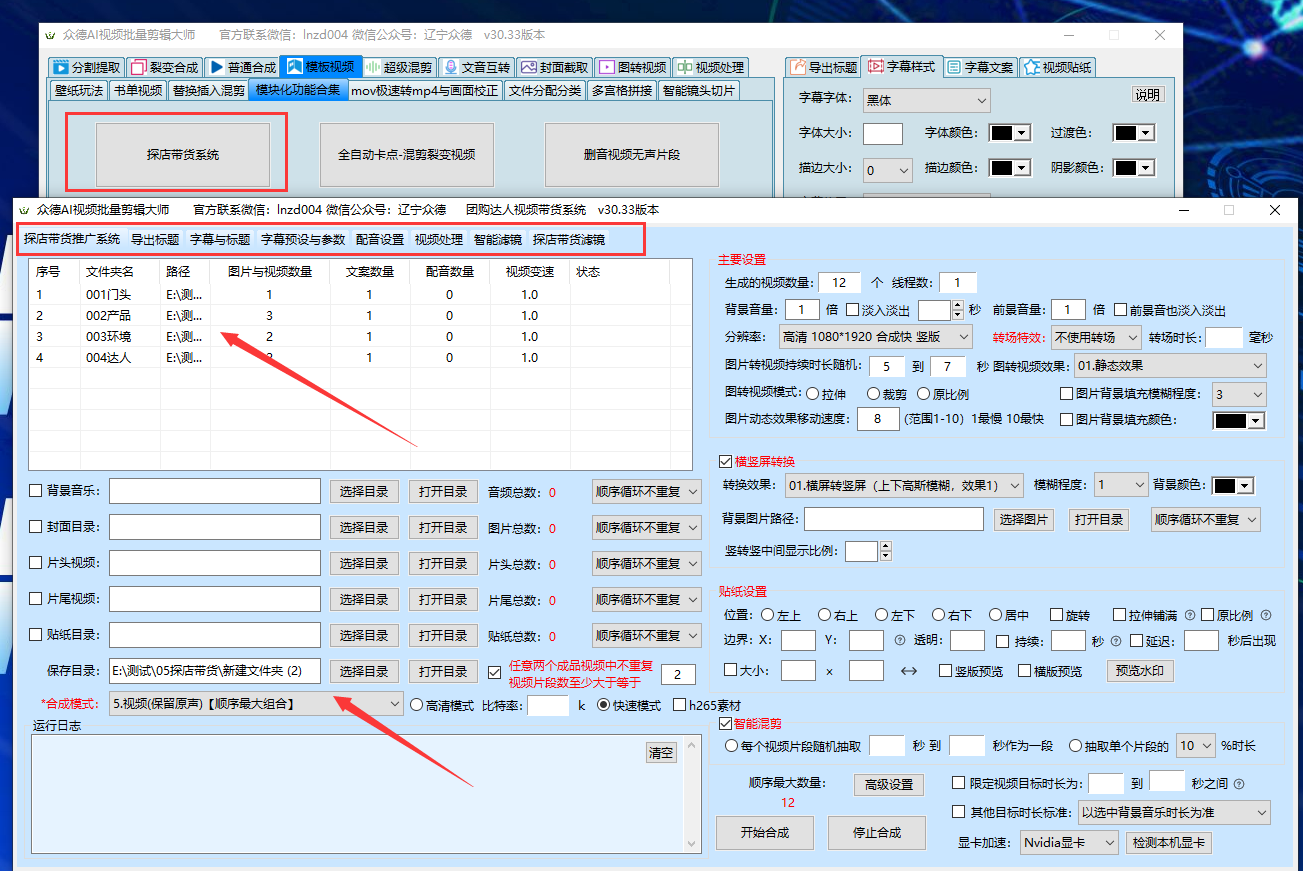
众德全自动批量剪辑工具,批量去重伪原创视频,全自动合成探店带货等视频
众德全自动批量剪辑工具已连续更新两年,服务了大大小小的自媒体公司工作室共200多个,成就了几百个草根创业者,实现月入10万,自从创办众德传媒之前,我一直坚信自媒体才是年轻草根创业者的出路,不需要技术门槛…...

【项目精选】基于网络爬虫技术的网络新闻分析(论文+源码+视频)
基于网络爬虫技术的网络新闻分析主要用于网络数据爬取。本系统结构如下: (1)网络爬虫模块。 (2)中文分词模块。 (3)中3文相似度判定模块。 (4)数据结构化存储模块。 &…...
)
华为OD机试 - 任务混部(JS)
任务混部 题目 公司创新实验室正在研究如何最小化资源成本,最大化资源利用率,请你设计算法帮他们解决一个任务混部问题:有taskNum项任务,每个任务有开始时间(startTime),结束时间(endTime),并行度(parallelism)三个属性,并行度是指这个任务运行时将会占用的服务…...
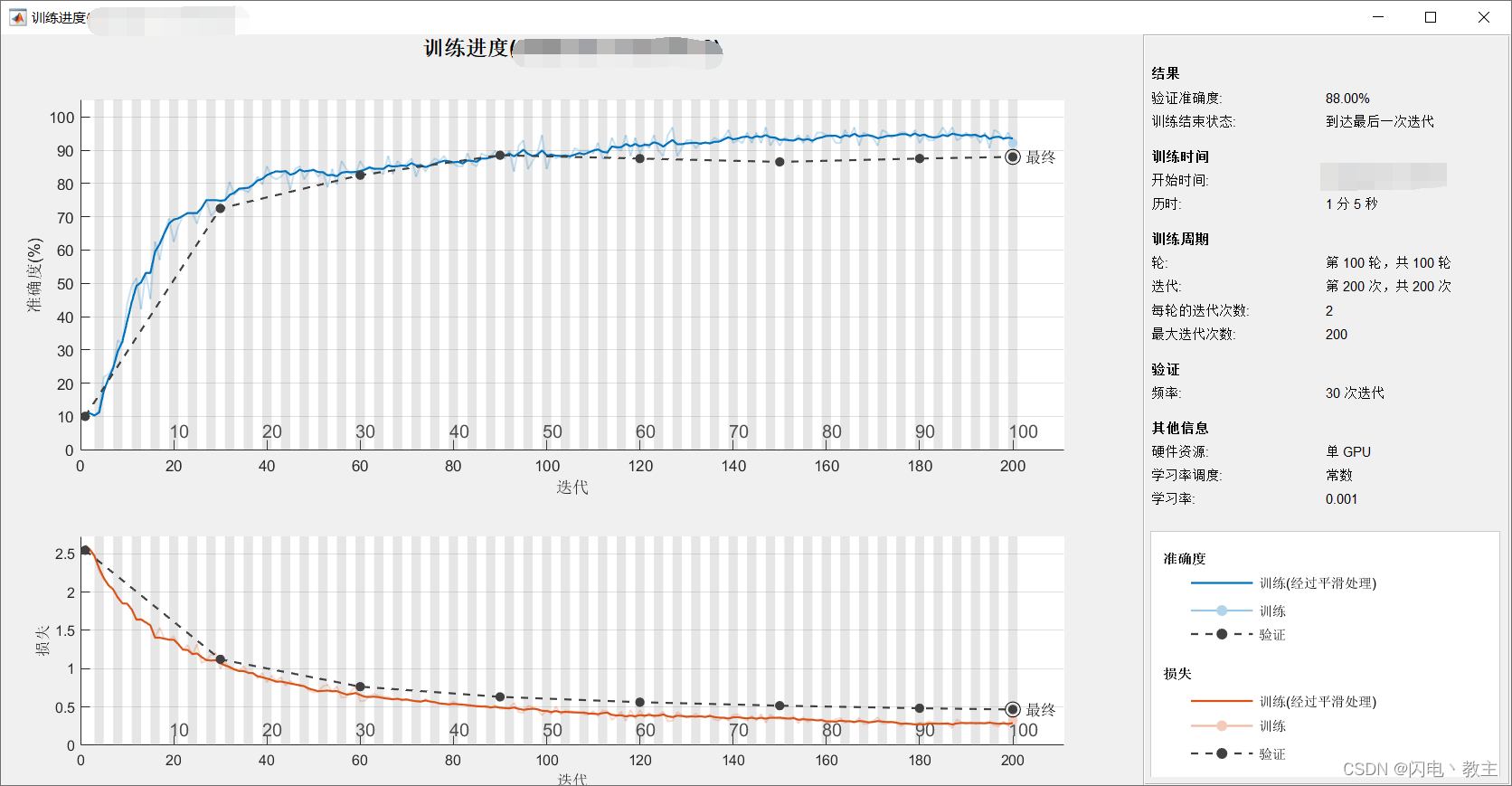
Matlab搭建AlexNet实现手写数字识别
Matlab搭建AlexNet实现手写数字识别 个人博客地址 文章目录Matlab搭建AlexNet实现手写数字识别环境内容步骤准备MNIST数据集数据预处理定义网络模型定义训练超参数网络训练和预测代码下载环境 Matlab 2020aWindows10 内容 使用Matlab对MNIST数据集进行预处理,搭建…...
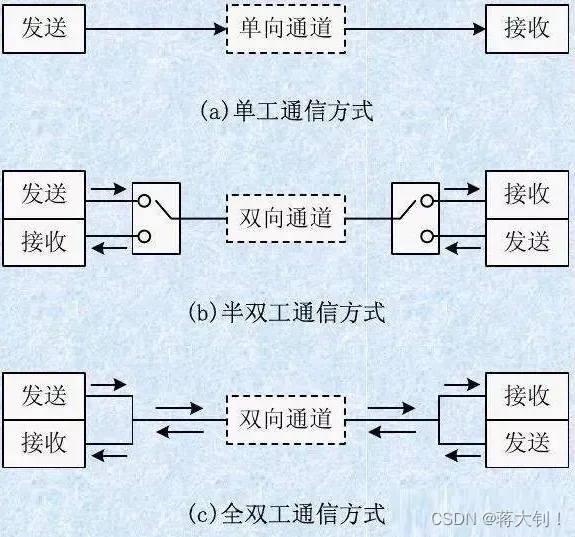
比较全面的HTTP和TCP网络传输的单工、全双工和半双工
文章目录单工、全双工、半双工1. 单工2. 半双工3. 全双工HTTP协议的工作模式TCP协议的工作模式本文参考: 图解网络传输单工、半双工、全双工 - 知乎 (zhihu.com) 问:HTTP是单工的还是双工的还是半双工的 - 简书 (jianshu.com) 关于TCP全双工模式的解释_忙…...

CSS Houdini
前言 最近看了几篇文章,是关于 CSS Houdini 的。作为一个前端搬砖的还真不知道这玩意,虽然不知道的东西挺多的,但是这玩意有点高大上啊。 Houdini 是一组底层 API,它们公开了 CSS 引擎的各个部分,从而使开发人员能够通…...

C++引用
这里写目录标题引用引用的基本使用引用做函数参数引用作为函数返回值引用的本质常量引用引用与指针的区别&的三种作用引用 引用的基本使用 作用: 给变量起别名 语法: 数据类型 &别名 原名 引用的本质是给变量起别名,因此࿰…...
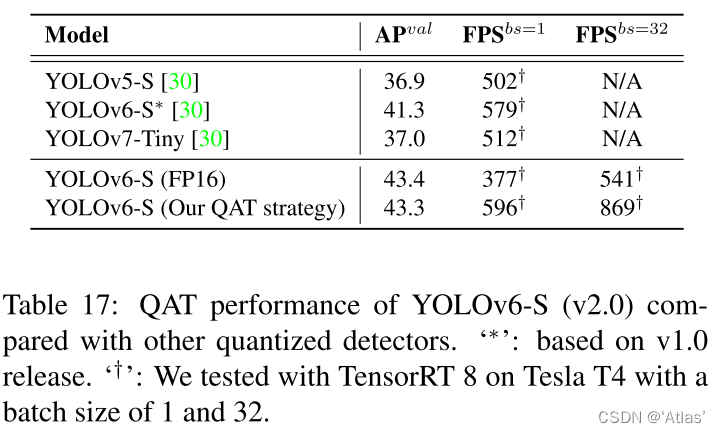
YOLOv6-目标检测论文解读
文章目录摘要问题算法网络设计BackboneNeckHead标签分配SimOTA(YOLOX提出):TAL(Task alignment learning,TOOD提出)损失函数分类损失框回归损失目标损失行业有用改进自蒸馏图像灰度边界填充量化及部署实验消…...

【factoryio】使用SCL编写 <机械手控制> 程序
使用虚拟工厂软件和博图联合仿真来编写【scl】机械手控制程序 文章目录 目录 文章目录 前言 二、程序编写 1.机械手运行部分 2.启动停止部分 3.急停复位部分 三、完整代码 总结 前言 在前面我们一起写过了许多案例控制的编写,在这一章我们一起来编写一下一个…...

QT学习记录散件
fromLocal8Bit() qt中fromLocal8Bit()函数可以设置编码。 因为QT默认的编码是unicode,不能显示中文的 而windows默认使用(GBK/GB2312/GB18030) 所以使用fromLocal8Bit()函数,可以实现从本地字符集GB到Unicode的转换,从…...
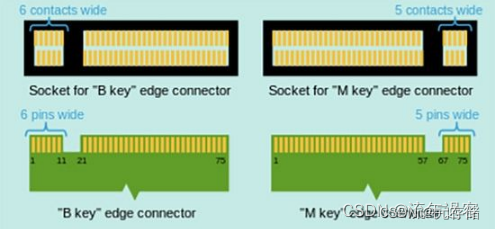
[SSD科普之1] PCIE接口详解及应用模式
PCI-Express(peripheral component interconnect express)是一种高速串行计算机扩展总线标准,它原来的名称为“3GIO”,是由英特尔在2001年提出的,旨在替代旧的PCI,PCI-X和AGP总线标准。一、PCI-E x1/x4/x8/x16插槽模式PCI-E有 x1/…...
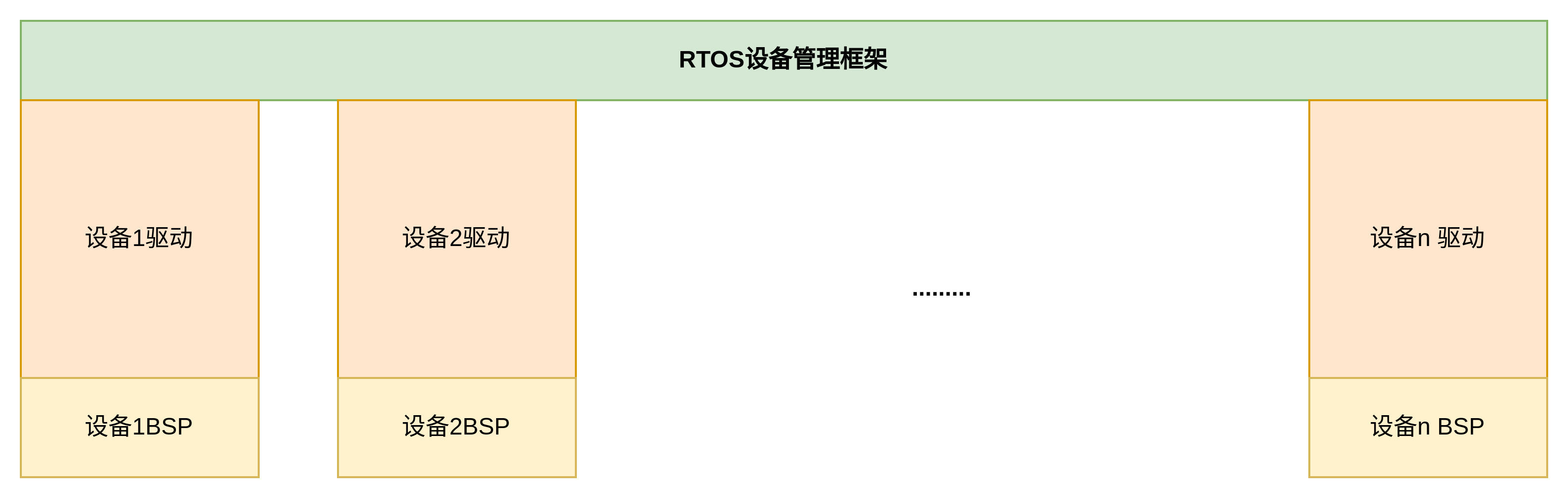
Linux设备驱动模型与 sysfs实现分析
RTOS和Linux系统上开发驱动的方式非常的不同,在RTOS系统下,驱动和驱动之间并没有实质性的联系,不同的驱动和BSP之间仅仅通过一层很薄很薄的设备管理框架聚合在一起构成RTOS的设备管理子系统。图形化表示如下: 设备驱动&BSP之间互相独立,互不影响,互不依赖,独立实现,…...

软考高级之制定备考计划
制定备考计划 高项准备时间最好是三个月以上,分为三个阶段来复习。 第一个阶段——熟悉知识点 第二个阶段——刷题 第三个阶段——冲刺复习 具体操作 第一个阶段 这个阶段的复习以教材和视频为主,掌握重要知识点。基础知识要打牢。例如࿱…...

[Pytorch] Linear层输出nan
参考链接: https://discuss.pytorch.org/t/well-formed-input-into-a-simple-linear-layer-output-nan/74720/11 总结原因: numpy需要更新 PS. 查看numpy版本号 打开Anaconda Prompt 进入环境 输入命令conda activate envname 然后输入pip show numpy…...

深入剖析AI大模型:大模型时代的 Prompt 工程全解析
今天聊的内容,我认为是AI开发里面非常重要的内容。它在AI开发里无处不在,当你对 AI 助手说 "用李白的风格写一首关于人工智能的诗",或者让翻译模型 "将这段合同翻译成商务日语" 时,输入的这句话就是 Prompt。…...

uni-app学习笔记二十二---使用vite.config.js全局导入常用依赖
在前面的练习中,每个页面需要使用ref,onShow等生命周期钩子函数时都需要像下面这样导入 import {onMounted, ref} from "vue" 如果不想每个页面都导入,需要使用node.js命令npm安装unplugin-auto-import npm install unplugin-au…...

零基础设计模式——行为型模式 - 责任链模式
第四部分:行为型模式 - 责任链模式 (Chain of Responsibility Pattern) 欢迎来到行为型模式的学习!行为型模式关注对象之间的职责分配、算法封装和对象间的交互。我们将学习的第一个行为型模式是责任链模式。 核心思想:使多个对象都有机会处…...

SpringCloudGateway 自定义局部过滤器
场景: 将所有请求转化为同一路径请求(方便穿网配置)在请求头内标识原来路径,然后在将请求分发给不同服务 AllToOneGatewayFilterFactory import lombok.Getter; import lombok.Setter; import lombok.extern.slf4j.Slf4j; impor…...

多种风格导航菜单 HTML 实现(附源码)
下面我将为您展示 6 种不同风格的导航菜单实现,每种都包含完整 HTML、CSS 和 JavaScript 代码。 1. 简约水平导航栏 <!DOCTYPE html> <html lang"zh-CN"> <head><meta charset"UTF-8"><meta name"viewport&qu…...

OPenCV CUDA模块图像处理-----对图像执行 均值漂移滤波(Mean Shift Filtering)函数meanShiftFiltering()
操作系统:ubuntu22.04 OpenCV版本:OpenCV4.9 IDE:Visual Studio Code 编程语言:C11 算法描述 在 GPU 上对图像执行 均值漂移滤波(Mean Shift Filtering),用于图像分割或平滑处理。 该函数将输入图像中的…...

保姆级教程:在无网络无显卡的Windows电脑的vscode本地部署deepseek
文章目录 1 前言2 部署流程2.1 准备工作2.2 Ollama2.2.1 使用有网络的电脑下载Ollama2.2.2 安装Ollama(有网络的电脑)2.2.3 安装Ollama(无网络的电脑)2.2.4 安装验证2.2.5 修改大模型安装位置2.2.6 下载Deepseek模型 2.3 将deepse…...

接口自动化测试:HttpRunner基础
相关文档 HttpRunner V3.x中文文档 HttpRunner 用户指南 使用HttpRunner 3.x实现接口自动化测试 HttpRunner介绍 HttpRunner 是一个开源的 API 测试工具,支持 HTTP(S)/HTTP2/WebSocket/RPC 等网络协议,涵盖接口测试、性能测试、数字体验监测等测试类型…...

【Linux系统】Linux环境变量:系统配置的隐形指挥官
。# Linux系列 文章目录 前言一、环境变量的概念二、常见的环境变量三、环境变量特点及其相关指令3.1 环境变量的全局性3.2、环境变量的生命周期 四、环境变量的组织方式五、C语言对环境变量的操作5.1 设置环境变量:setenv5.2 删除环境变量:unsetenv5.3 遍历所有环境…...

Docker拉取MySQL后数据库连接失败的解决方案
在使用Docker部署MySQL时,拉取并启动容器后,有时可能会遇到数据库连接失败的问题。这种问题可能由多种原因导致,包括配置错误、网络设置问题、权限问题等。本文将分析可能的原因,并提供解决方案。 一、确认MySQL容器的运行状态 …...