【学会动态规划】最大子数组和(19)
目录
动态规划怎么学?
1. 题目解析
2. 算法原理
1. 状态表示
2. 状态转移方程
3. 初始化
4. 填表顺序
5. 返回值
3. 代码编写
写在最后:
动态规划怎么学?
学习一个算法没有捷径,更何况是学习动态规划,
跟我一起刷动态规划算法题,一起学会动态规划!
1. 题目解析
题目链接:53. 最大子数组和 - 力扣(LeetCode)

题目很好理解,顾名思义,就是找最大的子数组和。
2. 算法原理
1. 状态表示
dp [ i ] 位置表示以 i 位置元素为结尾的所有子数组的最大和。
2. 状态转移方程
状态转移方程有两种情况,
1. 子数组长度为 1 时,最大和就是 i 位置的值
2. 子数组长度大于 1 是,最大和就是上一个位置的最大和 + 当前位置的值
所以我们就可以得出状态转移方程
dp [ i ] = max( nums[ i ],dp[ i ] + nums[ i ] )
3. 初始化
初始化就是防止越界,并且不影响后面的值,
初始化成 0 即可。
4. 填表顺序
从左往右即可。
5. 返回值
返回整个 dp 表里的最大值。
3. 代码编写
class Solution {
public:int maxSubArray(vector<int>& nums) {int n = nums.size();vector<int> dp(n + 1);int ans = INT_MIN;for(int i = 1; i <= n ; i++) {dp[i] = max(nums[i - 1], dp[i - 1] + nums[i - 1]);ans = max(ans, dp[i]);}return ans;}
};写在最后:
以上就是本篇文章的内容了,感谢你的阅读。
如果感到有所收获的话可以给博主点一个赞哦。
如果文章内容有遗漏或者错误的地方欢迎私信博主或者在评论区指出~
相关文章:

【学会动态规划】最大子数组和(19)
目录 动态规划怎么学? 1. 题目解析 2. 算法原理 1. 状态表示 2. 状态转移方程 3. 初始化 4. 填表顺序 5. 返回值 3. 代码编写 写在最后: 动态规划怎么学? 学习一个算法没有捷径,更何况是学习动态规划, 跟我…...

怎么做Tik Tok海外娱乐公会呢?新加坡市场怎么样?
一、为什么选择TikTok直播 1. 海外市场潜力巨大 • 自2016年始,多家直播平台陆续拓展至东南亚、中东、俄罗斯、日韩、欧美、拉美等地区。 • 海外市场作为直播发展新蓝海,2021年直播行业整申请cmxyci体规模达百亿美元,并维持高速增长。 &a…...
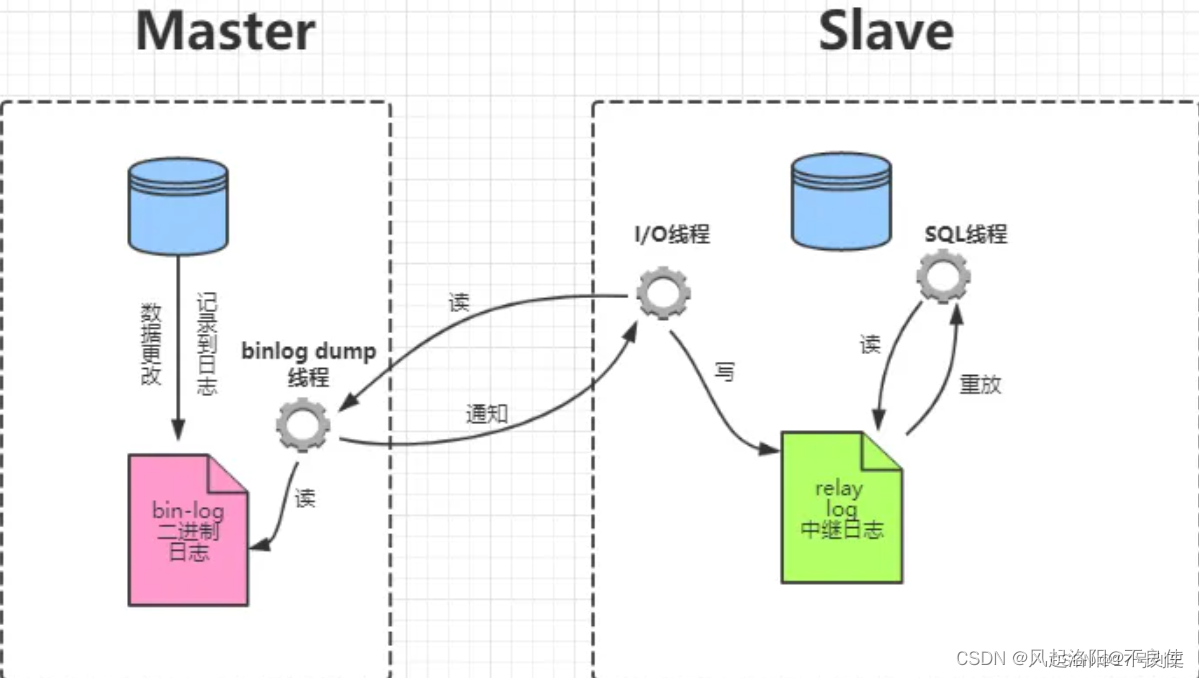
mysql主从复制搭建
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 前言MySQL复制过程分为三部: 一、准备工作二、配置>主库Master三、配置>从库SlaveSlave_IO_Running: YesSlave_SQL_Running: Yes 四、测试至此&am…...
Java:正则表达式案例:爬数据,重复数据替换,数据分割
使用正则表达式查找一段文本中的内容 需求:请把下面文本中的电话,邮箱,座机号码,热线都爬取出来。 String data "电话:1866668888,18699997777\n" "或者联系邮箱: boniuitcast.cn,\n" "座机…...

CF 765D Artsem and Saunders 构造
CF765D Artsem and Saunders 直接猜一种构造做法, h ( x ) h(x) h(x)的值域一定和 f ( x ) f(x) f(x)的值域一样,我们先满足 h ( g ( x ) ) f ( x ) h(g(x))f(x) h(g(x))f(x)这个条件,遍历 f ( x ) f(x) f(x),每次添加 h ( x ) h…...
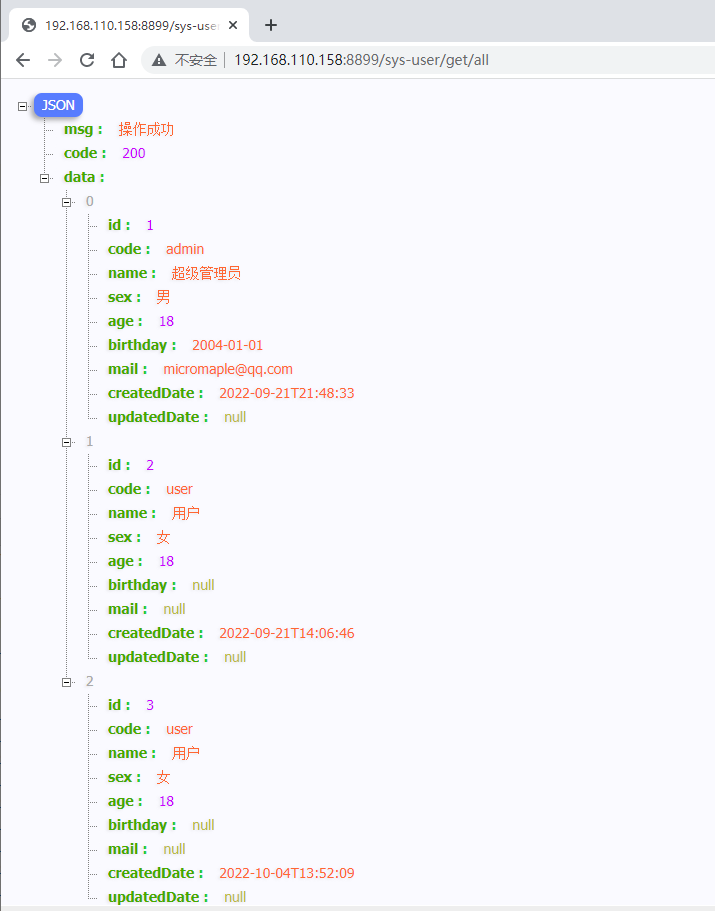
DevOps系列文章 之 SpringBoot整合GitLab-CI实现持续集成
在企业开发过程中,我们开发的功能或者是修复的BUG都需要部署到服务器上去,而这部分部署操作又是重复且繁琐的工作,GitLab-CI 持续集成为我们解决了这一痛点,将重复部署的工作自动化,大大的节省了程序员们的宝贵时间。本…...

K8S系列二:实战入门
I. 配置kubectl 1.1 什么是kubectl? 官方文档中介绍kubectl是: Kubectl 是一个命令行接口,用于对 Kubernetes 集群运行命令。Kubectl的配置文件在$HOME/.kube目录。我们可以通过设置KUBECONFIG环境变量或设置命令参数–kubeconfig来指定其他…...

form中表单切换,导致 relus 中的事件无法触发,原因:页面切换不要一直切换DOM,会导致问题,需要都显示出来
修改前,因为重复渲染DOM导致绑定rules失效 修改前代码使用 computed 计算出渲染的DOM,影响rules事件<el-formref"form"inline:model"billDetailCopy":rules"rules"size"small"label-position"right&quo…...

Android Ble蓝牙App(五)数据操作
Ble蓝牙App(五)数据操作 前言正文一、操作内容处理二、读取数据① 概念② 实操 三、写入数据① 概念② 实操 四、打开通知一、概念二、实操三、收到数据 五、源码 前言 关于低功耗蓝牙的服务、特性、属性、描述符都已经讲清楚了,而下面就是使…...
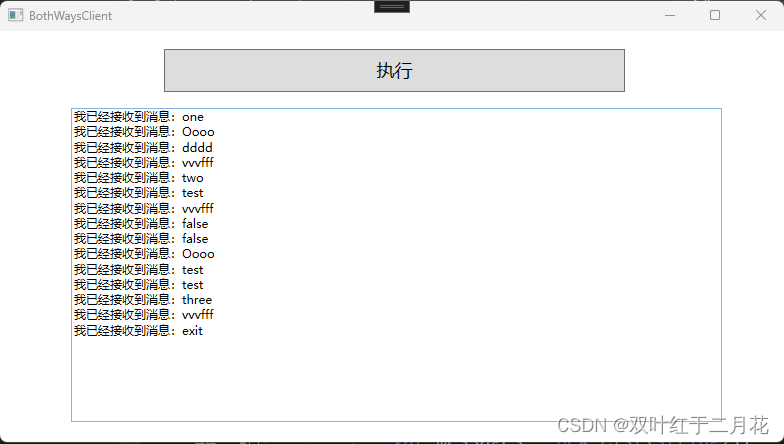
.netcore grpc双向流方法详解
一、双向流处理概述 简单来讲客户端可以向服务端发送消息流,服务端也可以向客户端传输响应流,即客户端和服务端可以互相通讯客户端无需发送消息即可开始双向流式处理调用 。 客户端可选择使用 RequestStream.WriteAsync 发送消息。 使用 ResponseStream…...

【Servlet】(Servlet API HttpServlet 处理请求 HttpServletRequest 打印请求信息 前端给后端传参)
文章目录 Servlet APIHttpServlet处理请求 HttpServletRequest打印请求信息前端给后端传参 Servlet API Servlet中常用的API HttpServlet 实际开发的时候主要重写 doXXX 方法, 很少会重写 init / destory / service destory 服务器终止的时候会调用. //下面的注解把当前类和…...
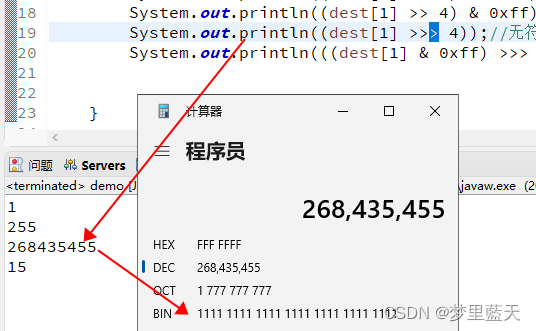
java中右移>>和无符号右移>>>的区别
public static void main(String[] args) {byte[] dest new byte[2];dest[0] 0x15; //0001 0101dest[1] (byte) 0xfb;//1111 1011System.out.println((dest[0] >> 4) & 0xff);//右移 应该是0000 0001 十进制结果显示1 结果也是1,正确System.out.printl…...

牛客周赛 Round 7
目录 A 游游的you矩阵 题目: 题解: AC 代码: B 游游的01串操作 题目: 题解: AC 代码: C 游游的正整数 题目: 题解: AC 代码: D 游游的选数乘积 题目…...
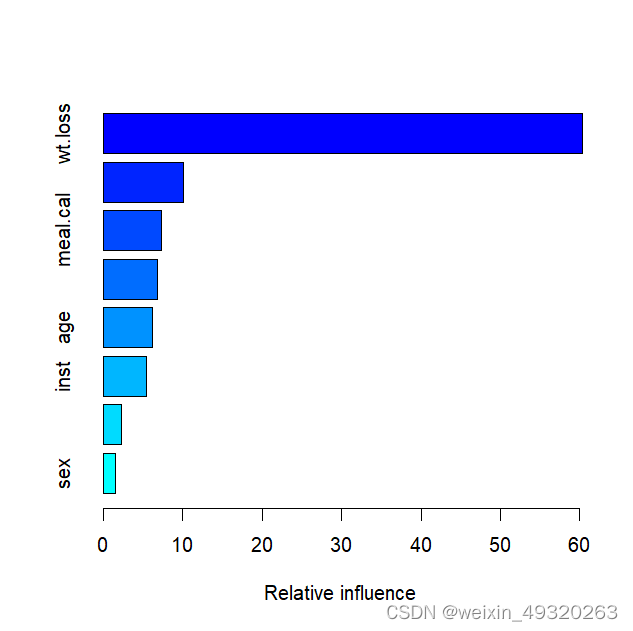
R语言生存分析(机器学习)(1)——GBM(梯度提升机)
GBM是一种集成学习算法,它结合了多个弱学习器(通常是决策树)来构建一个强大的预测模型。GBM使用“Boosting”的技术来训练弱学习器,这种技术是一个迭代的过程,每一轮都会关注之前轮次中预测效果较差的样本,…...

k8s和docker简单介绍
当涉及到容器技术和容器编排时,Docker和Kubernetes是两个重要的概念。我将更详细地介绍它们以及它们之间的关系。 Docker: Docker是一种容器化技术,它允许你将应用程序及其依赖项打包到一个称为"容器"的封闭环境中。每个容器都包…...
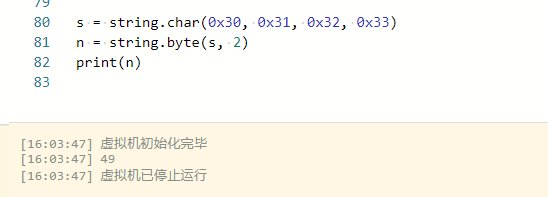
Lua学习记录
Lua基础了解 Lua的注释通过 (-- 单行注释,--[[ ]] 多行注释)可以不加; 多个变量赋值,按顺序赋值,没有则为nil; function的简单用法,多个返回值配合多重赋值,以end为结束标志 Lua下标从1开始&…...

三分钟完美解决你的C盘内存过大爆红
一、清理回收站 二、清理桌面 建议一 不要在桌面放太多图标或者文件会占用过多的内存,可以放到其他盘建议二、 将位置移动到别的盘 三、手动删除下载文件与缓存文件 日常使用中会通过Windows下载各种文件资料到电脑中,它默认也是直接下载在C盘中的。如果我们在以…...
)
C++ - equal(比较两个vector元素)
C标准库的std::equal函数。这个函数用于比较两个范围的元素是否相等。 在使用std::equal函数时,您需要提供两个范围的迭代器,以及一个可选的谓词函数(predicate)。函数会比较第一个范围内的元素和第二个范围内的元素是否相等。如果…...

多线程:线程池
线程池 提前创建多个线程放入线程池中,使用时直接获取,使用完直接放入池中;可以避免频繁创建销毁,实现重复利用,类似生活中的公共交通工具。好处:提高相应速度;降低资源消耗;便于线…...

9.3.2.2网络原理(传输层TCP)
TCP全部细节参考RFC标准文档 一.TCP特点: 有连接,可靠传输,面向字节流,全双工. 二.TCP数据报: 1.端口号是传输层的重要概念. 2.TCP的报头是变长的(UDP是固定的8字节),大小存在4位首部长度中,用4个bit位(0~15)表示长度单位是4字节.(TCP报头最大长度是60字节,前面20字节是固定…...

【Linux】shell脚本忽略错误继续执行
在 shell 脚本中,可以使用 set -e 命令来设置脚本在遇到错误时退出执行。如果你希望脚本忽略错误并继续执行,可以在脚本开头添加 set e 命令来取消该设置。 举例1 #!/bin/bash# 取消 set -e 的设置 set e# 执行命令,并忽略错误 rm somefile…...

Zustand 状态管理库:极简而强大的解决方案
Zustand 是一个轻量级、快速和可扩展的状态管理库,特别适合 React 应用。它以简洁的 API 和高效的性能解决了 Redux 等状态管理方案中的繁琐问题。 核心优势对比 基本使用指南 1. 创建 Store // store.js import create from zustandconst useStore create((set)…...

华为OD机试-食堂供餐-二分法
import java.util.Arrays; import java.util.Scanner;public class DemoTest3 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseint a in.nextIn…...

DIY|Mac 搭建 ESP-IDF 开发环境及编译小智 AI
前一阵子在百度 AI 开发者大会上,看到基于小智 AI DIY 玩具的演示,感觉有点意思,想着自己也来试试。 如果只是想烧录现成的固件,乐鑫官方除了提供了 Windows 版本的 Flash 下载工具 之外,还提供了基于网页版的 ESP LA…...

【android bluetooth 框架分析 04】【bt-framework 层详解 1】【BluetoothProperties介绍】
1. BluetoothProperties介绍 libsysprop/srcs/android/sysprop/BluetoothProperties.sysprop BluetoothProperties.sysprop 是 Android AOSP 中的一种 系统属性定义文件(System Property Definition File),用于声明和管理 Bluetooth 模块相…...

【Web 进阶篇】优雅的接口设计:统一响应、全局异常处理与参数校验
系列回顾: 在上一篇中,我们成功地为应用集成了数据库,并使用 Spring Data JPA 实现了基本的 CRUD API。我们的应用现在能“记忆”数据了!但是,如果你仔细审视那些 API,会发现它们还很“粗糙”:有…...

Python如何给视频添加音频和字幕
在Python中,给视频添加音频和字幕可以使用电影文件处理库MoviePy和字幕处理库Subtitles。下面将详细介绍如何使用这些库来实现视频的音频和字幕添加,包括必要的代码示例和详细解释。 环境准备 在开始之前,需要安装以下Python库:…...

数据库分批入库
今天在工作中,遇到一个问题,就是分批查询的时候,由于批次过大导致出现了一些问题,一下是问题描述和解决方案: 示例: // 假设已有数据列表 dataList 和 PreparedStatement pstmt int batchSize 1000; // …...

html css js网页制作成品——HTML+CSS榴莲商城网页设计(4页)附源码
目录 一、👨🎓网站题目 二、✍️网站描述 三、📚网站介绍 四、🌐网站效果 五、🪓 代码实现 🧱HTML 六、🥇 如何让学习不再盲目 七、🎁更多干货 一、👨…...

安全突围:重塑内生安全体系:齐向东在2025年BCS大会的演讲
文章目录 前言第一部分:体系力量是突围之钥第一重困境是体系思想落地不畅。第二重困境是大小体系融合瓶颈。第三重困境是“小体系”运营梗阻。 第二部分:体系矛盾是突围之障一是数据孤岛的障碍。二是投入不足的障碍。三是新旧兼容难的障碍。 第三部分&am…...
