【左神算法刷题班】第17节:在有序二维数组中查找目标值、等于目标字符串的子序列个数
第17节
题目1:在有序二维数组中查找目标值
给定一个每一行有序、每一列也有序,整体可能无序的二维数组
再给定一个数num,
返回二维数组中有没有num这个数
例子
数组如下,找 6 是否存在。
1 3 5 7
2 4 6 13
3 9 14 14
思路
力扣上做过原题。
从左下角开始,向右上角走。如果当前小于 target,则向右走。如果当前大于 target,则向上走。
题目2:
给定一个每一行有序、每一列也有序,整体可能无序的二维数组
在给定一个正数k,
返回二维数组中,整体第 k 小的数
Leetcode原题:
https://leetcode.com/problems/kth-smallest-element-in-a-sorted-matrix/
思路
1 3 5 7
2 4 6 13
3 9 14 14
假设我先任意选一个数字10,想要求出所有小于10的数有多少个。从右上角向左下角走,如果当前数小于10,就往下走(此时当前位置左方全是小于10的数),如果大于10,就往左走。沿途通过下标计算,累加所有小于10的数,假设有m个。
根据上述方式,我可以知道小于某个数字的数有多少个。
而整体来看,我知道整个数组最小值是左上角的 min,最大值是右下角的 max,这样我就可以通过二分查找的方式,让 mid=min+(max-min)/2,求出比 mid 小的数有 m 个,如果 m < k,就让 max = mid 继续二分;否则如果 m>k,让 min = mid 继续二分。
如果最后得到答案是 res,而整个数组中没有 res 这个数字,你需要找到距离 res 最近,并且比 res 小的数。
题目3
Leetcode原题:
https://leetcode.com/problems/palindrome-pairs/
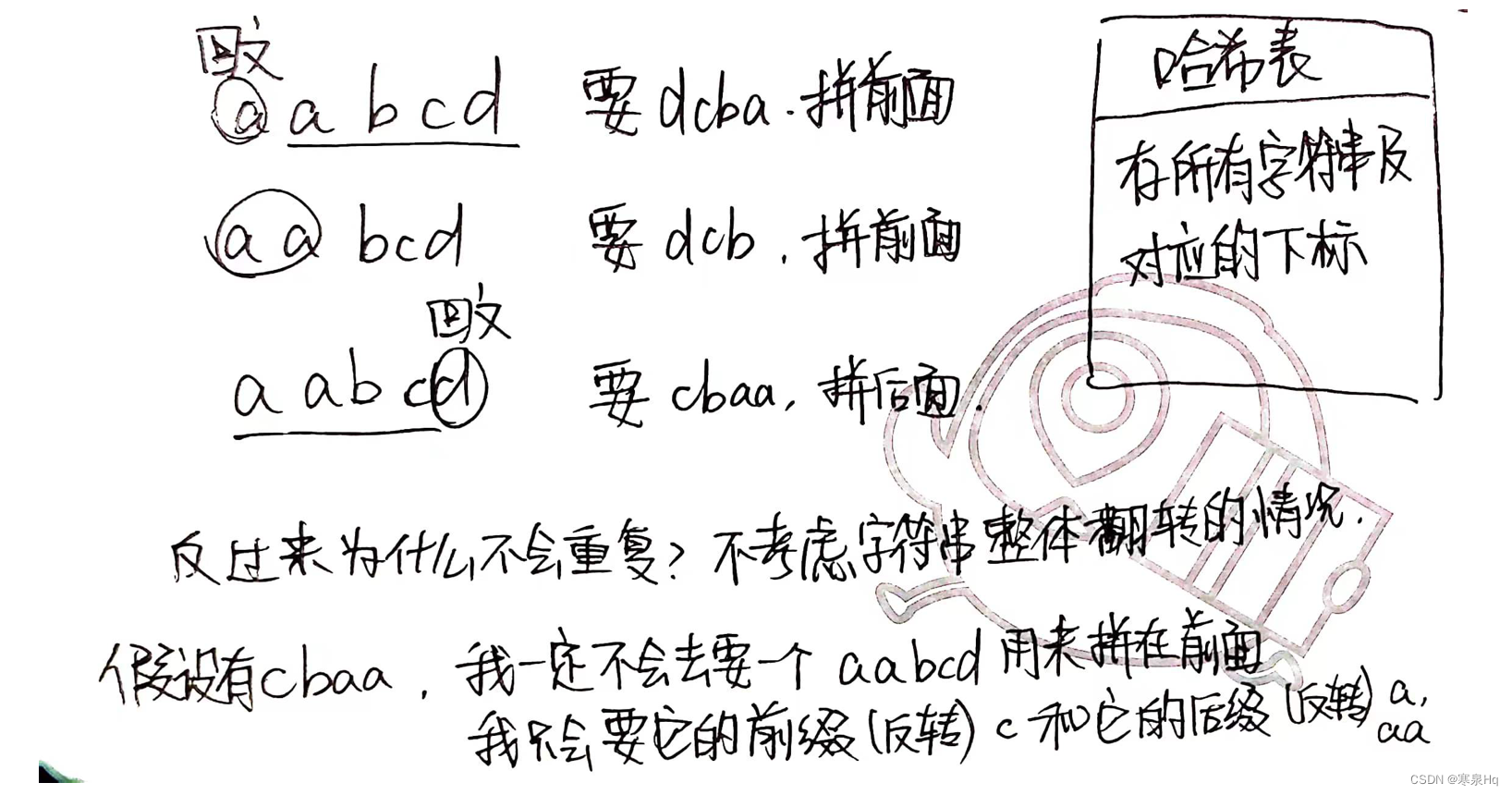
题目4:等于目标字符串的子序列个数(DP)
给定两个字符串S和T
返回S的所有子序列中
有多少个子序列的字面值等于T
思路
样本对应模型,可能性根据结尾字符来划分。
假设S的长度为i,T的长度为j,则 dp[i][j] 表示:从 S 序列 [0…i] 范围上随便选,有多少个子序列的字面值等于 T[0…j] 这个前缀字符串。
dp 表的右下角,就表示了 S 整体字符串有多少个子序列的字面值等于 T 字符串。
状态怎么转移?当我来到 dp[i][j] 的时候,
- 可能性1:不使用 i 位置的字符,则
dp[i][j] = dp[i-1][j] - 可能性2:只有在 S[i] == T[j] 的情况下才可以,使用 S 字符串 i 位置的字符来匹配 T 字符串 j 位置的字符,则
dp[i][j] = dp[i-1][j-1]
考虑上述两种可能性,相加,得到 dp[i][j] = dp[i-1][j] + dp[i-1][j-1]
public static int dp(String S, String T) {char[] s = S.toCharArray();char[] t = T.toCharArray();int N = s.length;int M = t.length;int[][] dp = new int[N][M];// s[0..0] T[0..0] dp[0][0]dp[0][0] = s[0] == t[0] ? 1 : 0;for (int i = 1; i < N; i++) {dp[i][0] = s[i] == t[0] ? (dp[i - 1][0] + 1) : dp[i - 1][0];}for (int i = 1; i < N; i++) {for (int j = 1; j <= Math.min(i, M - 1); j++) {dp[i][j] = dp[i - 1][j];if (s[i] == t[j]) {dp[i][j] += dp[i - 1][j - 1];}}}return dp[N - 1][M - 1];
}
题目5
给定一个字符串Str
返回Str的所有子序列中有多少不同的字面值
Leetcode原题:
https://leetcode.com/problems/distinct-subsequences-ii/
思路
主要是观察规律。
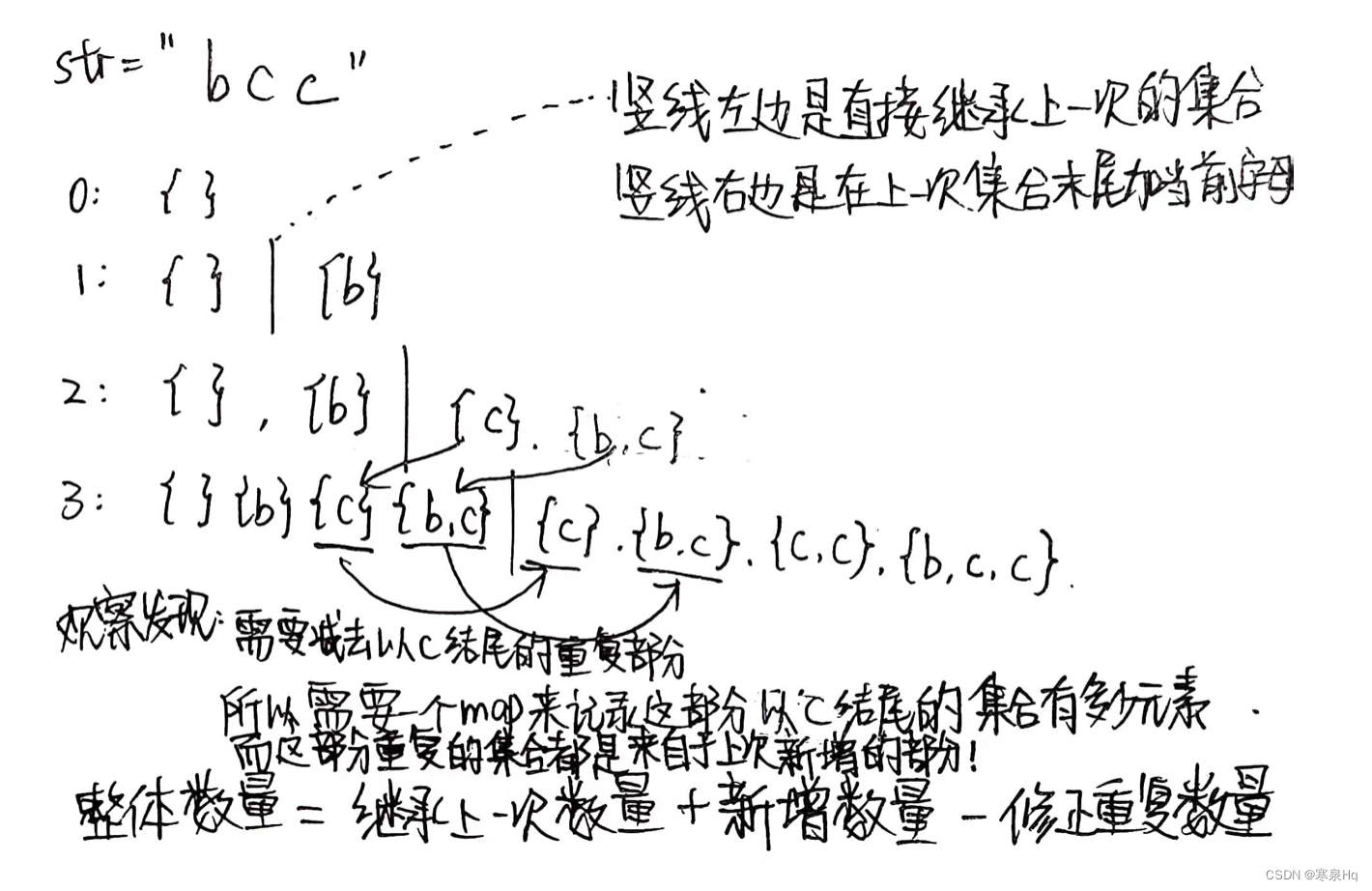
题目6
给定一个数组arr,长度为N,arr中的值只有1,2,3三种
arr[i] == 1,代表汉诺塔问题中,从上往下第i个圆盘目前在左
arr[i] == 2,代表汉诺塔问题中,从上往下第i个圆盘目前在中
arr[i] == 3,代表汉诺塔问题中,从上往下第i个圆盘目前在右
那么arr整体就代表汉诺塔游戏过程中的一个状况
如果这个状况不是汉诺塔最优解运动过程中的状况,返回-1
如果这个状况是汉诺塔最优解运动过程中的状况,返回它是第几个状况
题目7
Leetcode 原题:
https://leetcode.com/problems/shortest-bridge/
相关文章:

【左神算法刷题班】第17节:在有序二维数组中查找目标值、等于目标字符串的子序列个数
第17节 题目1:在有序二维数组中查找目标值 给定一个每一行有序、每一列也有序,整体可能无序的二维数组 再给定一个数num, 返回二维数组中有没有num这个数 例子 数组如下,找 6 是否存在。 1 3 5 7 2 4 6 13 3 9 14 …...
)
【Terraform学习】本地变量(Terraform配置语言学习)
背景: 关于如何在机器上拉terraform代码,初始化就不重复了,需要的可以查看前面的文章: 【Terraform学习】Terraform-AWS部署快速入门(快速入门)_向往风的男子的博客-CSDN博客 使用本地变量命名资源 将每…...
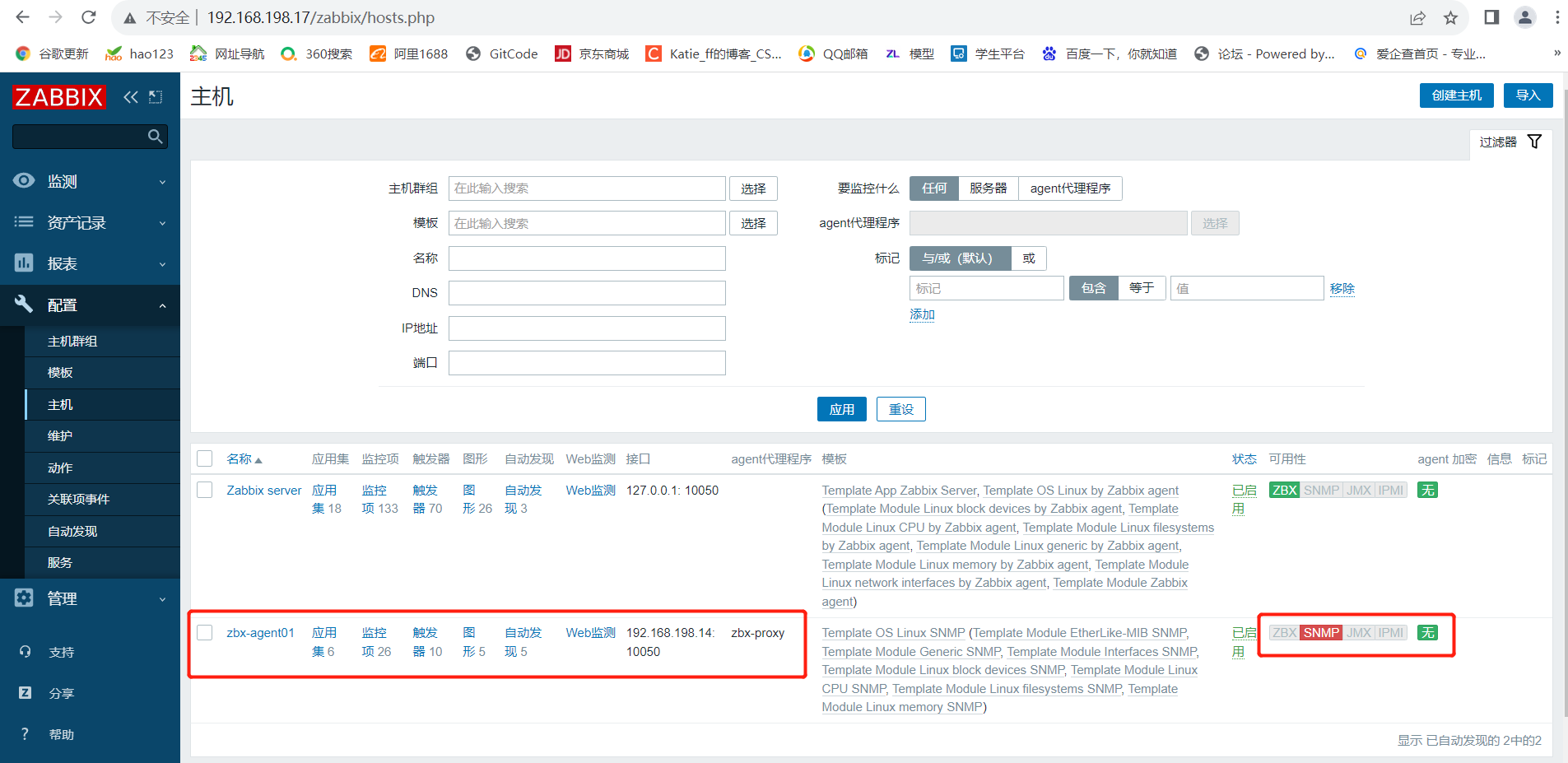
zabbix自动注册服务器以及部署代理服务器
文章目录 Zabbix自动注册服务器及部署代理服务器一.zabbix自动注册1.什么是自动注册2.环境准备3.zabbix客户端配置4.在 Web 页面配置自动注册5.验证自动注册 二.部署 zabbix 代理服务器1.分布式监控的作用:2.环境部署3.代理服务器配置4.客户端配置5.web页面配置5.1 …...

掌握Python的X篇_32_使用python编辑pdf文件_pdfrw
本篇介绍利用python操作pdf文件,我们平时也会有合并和拆分pdf的需求,此时我们就可以使用本节内容。 文章目录 1. pdfrw的安装2. 切分pdf文件3. pdfrw官网及实现一版四面的实例 1. pdfrw的安装 pip install pdfrw官网地址:https://github.co…...

【软件工程】软件测试
软件测试的对象 软件程序文档 测试对象:各个阶段产生的源程序和文档。 软件测试的目的 基于不同的立场,对软件测试的目的存在着两种完全对立的观点。 (1)一种观点是通过测试暴露出软件中所包含的故障和缺陷(从用户的角度)…...
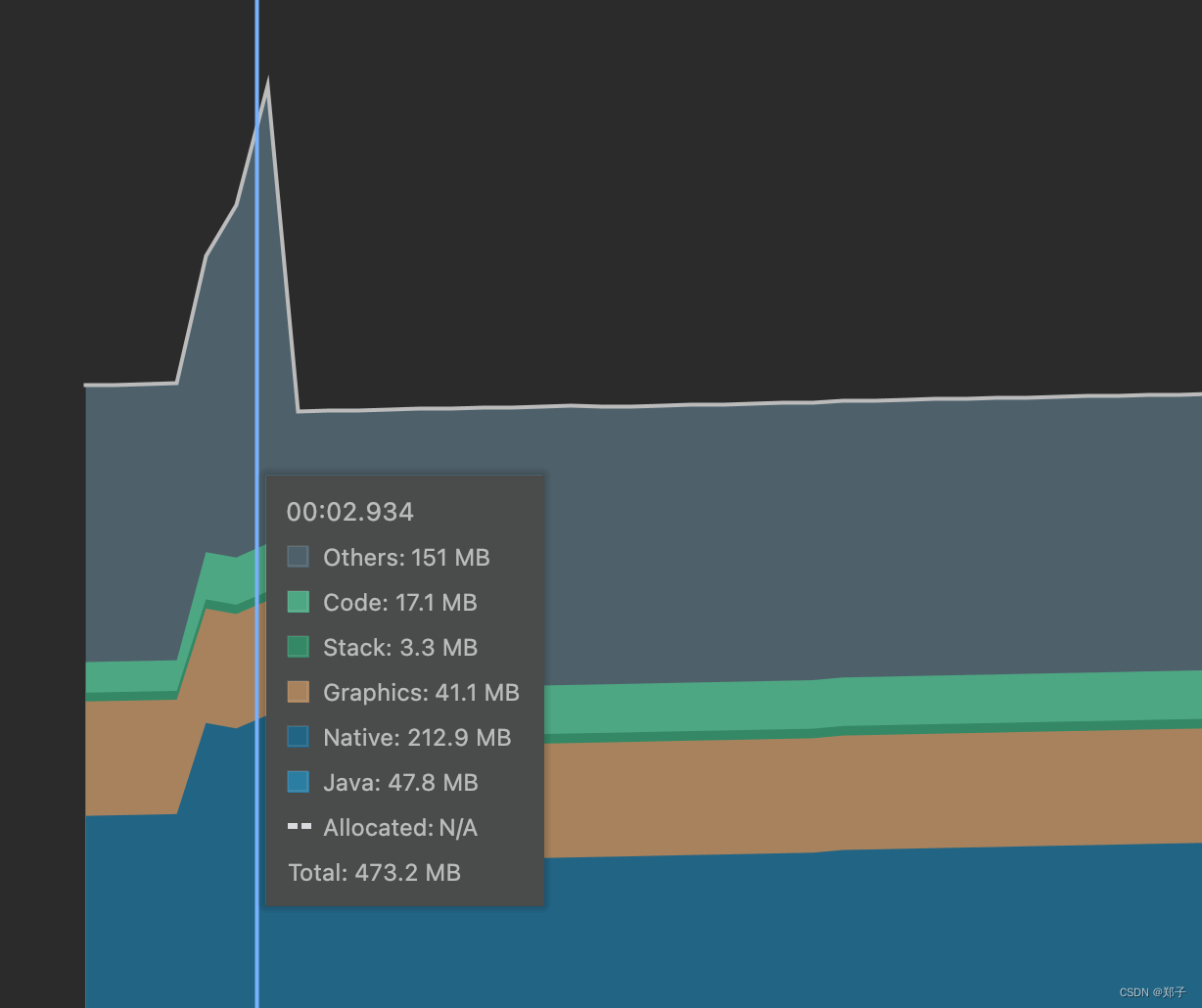
Android性能优化——内存优化
一、内存问题 内存抖动,锯齿状,GC导致卡顿内存泄漏,可用内存减少,频繁GC 内存溢出,OOM,程序异常 二、内存分析工具 Memory ProfilerMemory Analyzer LeakCanary Memory Profiler 实时图表展示应用内存使…...

Android Studio实现图形验证码
源代码 源代码MainActivity 效果图32行需要修改,不修改会报错:需要常量表达式,我的代码已修改 点击后 MainActivity import static com.example.graphicverificationcode.RxCaptcha.TYPE.NUMBER;import android.annotation.SuppressLint; …...

JAVA面试数据库篇
目录 一.优化 1.MYSQL中,如何定位慢查询? 2.SQL语句执行慢,如何分析呢? 3.索引 了解过索引吗?(什么是索引) 索引的底层数据结构了解过吗? B树和B树的区别是什么呢? 什么是聚…...

Android高手进阶教程(三)之----Android 中自定义View的应用.
大家好我们今天的教程是在Android 教程中自定义View 的学习,对于初学着来说,他们习惯了Android 传统的页面布局方式,如下代码: <?xml version"1.0" encoding"utf-8"?> <LinearLayout xmlns:android"htt…...

第一百一十三回 dart中的getter/setter方法
文章目录 概念介绍使用方法示例代码使用扩展 我们在上一章回中介绍了 flutter_screenutil包相关的内容,本章回中将介绍 dart中的setter/getter方法.闲话休提,让我们一起Talk Flutter吧。 概念介绍 我们在这里介绍的setter/getter方法属于编程语言中的…...

搭建Docker环境
目录 一、docker环境搭建 1、卸载旧版本docker 2、安装依赖和设置仓库 3、安装docker 4、启动并加入开机启动 5、验证是否安装成功 二、利用docker搭建nginx 1、拉取镜像 2、启动容器,部署nginx 一、docker环境搭建 1、卸载旧版本docker yum remove docke…...
微服务08-多级缓存
1.什么是多级缓存 传统的缓存策略一般是请求到达Tomcat后,先查询Redis,如果未命中则查询数据库,如图: 存在下面的问题: •请求要经过Tomcat处理,Tomcat的性能成为整个系统的瓶颈 •Redis缓存失效时,会对数据库产生冲击 多级缓存就是充分利用请求处理的每个环节,分…...

Intel汇编和ATT汇编的区别?
一、前缀不同 在 Intel 语法中,没有寄存器前缀或立即前缀。 然而,在 AT&T 中,寄存器的前缀是“%”,而 immed 的前缀是“$”。 Intel 语法十六进制或二进制即时数据分别带有“h”和“b”后缀。 此外,如果第一个十六…...
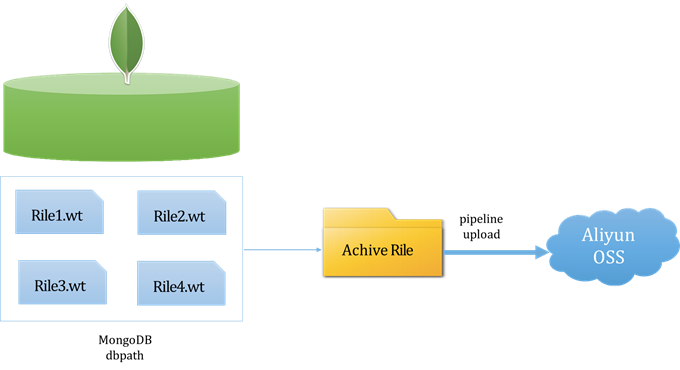
MongoDB 备份与恢复
1.1 MongoDB的常用命令 mongoexport / mongoimport mongodump / mongorestore 有以上两组命令在备份与恢复中进行使用。 1.1.1 导出工具mongoexport Mongodb中的mongoexport工具可以把一个collection导出成JSON格式或CSV格式的文件。可以通过参数指定导出的数据项,…...
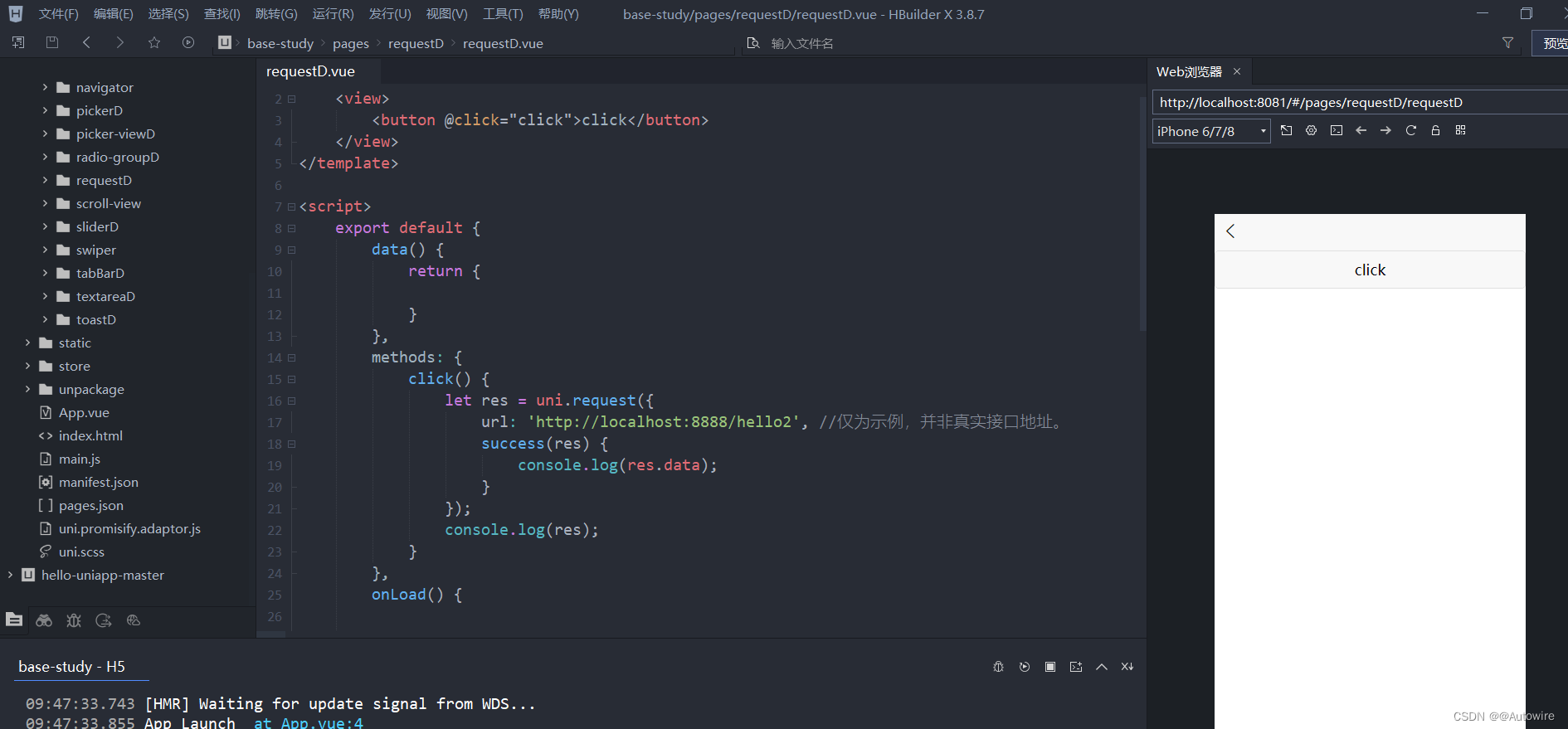
探讨uniapp的网络通信问题
uni-app 中有很多原生的 API,其中我们经常会用到的肯定有:uni.request(OBJECT) method 有效值 注意:method有效值必须大写,每个平台支持的method有效值不同,详细见下表。 success 返回参数说明 data 数据说明 最终…...
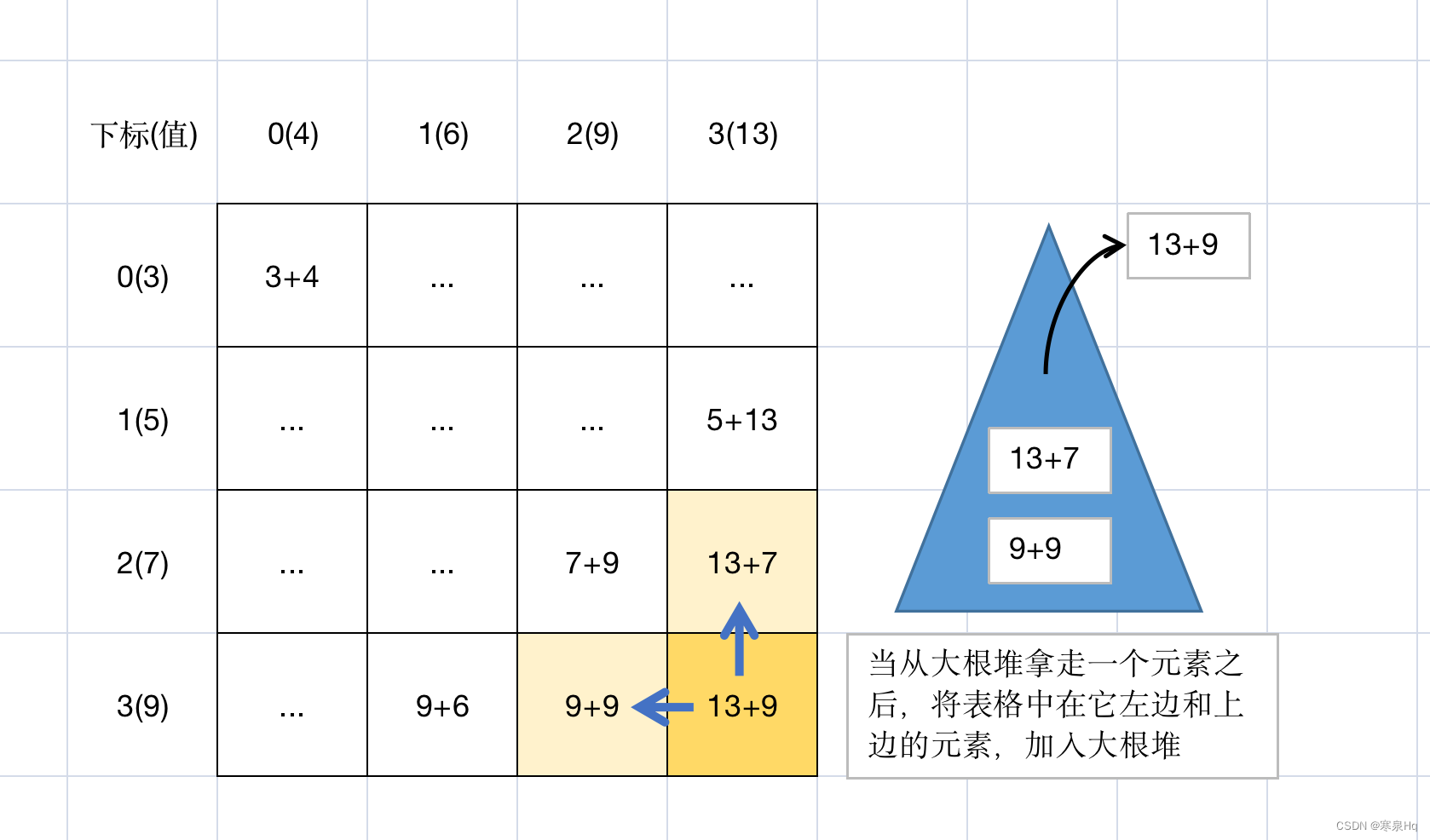
【左神算法刷题班】第18节:汉诺塔问题、岛屿问题、最大路径和问题
第18节 题目1:汉诺塔问题(变体) 体系学习班18节有讲暴力递归的汉诺塔原题。 给定一个数组arr,长度为N,arr中的值只有1,2,3三种 arr[i] 1,代表汉诺塔问题中,从上往下第…...
网络安全体系架构介绍
网络安全体系是一项复杂的系统工程,需要把安全组织体系、安全技术体系和安全管理体系等手段进行有机融合,构建一体化的整体安全屏障。针对网络安全防护,美国曾提出多个网络安全体系模型和架构,其中比较经典的包括PDRR模型、P2DR模…...

JSP实训项目设计报告—MVC简易购物商城
JSP实训项目设计报告—MVC简易购物商城 文章目录 JSP实训项目设计报告—MVC简易购物商城设计目的设计要求设计思路系统要求单点登录模块商品展示模块购物车展示模块 概要设计Model层View层Controller层 详细设计Model层View层登录界面系统主界面 Controller层 系统运行效果项目…...
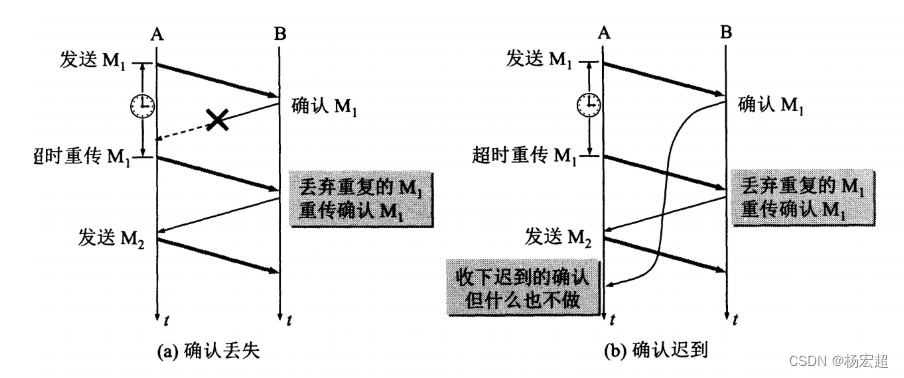
41、可靠传输——停等ARQ
前面两节内容我们学习了传输层的基本概况的一些知识,包括传输层在TCP/IP协议栈中负责的任务、传输层的两大协议,以及端口号、套接字等一些基本的概念。从这一节开始,我们将开启两大协议中TCP协议的学习。 但是,经过之前的学习&am…...

RK3568 cmake编译
一.简介 CMake是开源、跨平台的构建工具,可以让我们通过编写简单的配置文件去生成本地的Makefile,这个配置文件是独立于运行平台和编译器的,这样就不用亲自去编写Makefile了,而且配置文件可以直接拿到其它平台上使用,…...

【网络】每天掌握一个Linux命令 - iftop
在Linux系统中,iftop是网络管理的得力助手,能实时监控网络流量、连接情况等,帮助排查网络异常。接下来从多方面详细介绍它。 目录 【网络】每天掌握一个Linux命令 - iftop工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景…...

linux arm系统烧录
1、打开瑞芯微程序 2、按住linux arm 的 recover按键 插入电源 3、当瑞芯微检测到有设备 4、松开recover按键 5、选择升级固件 6、点击固件选择本地刷机的linux arm 镜像 7、点击升级 (忘了有没有这步了 估计有) 刷机程序 和 镜像 就不提供了。要刷的时…...

【决胜公务员考试】求职OMG——见面课测验1
2025最新版!!!6.8截至答题,大家注意呀! 博主码字不易点个关注吧,祝期末顺利~~ 1.单选题(2分) 下列说法错误的是:( B ) A.选调生属于公务员系统 B.公务员属于事业编 C.选调生有基层锻炼的要求 D…...

C++中string流知识详解和示例
一、概览与类体系 C 提供三种基于内存字符串的流,定义在 <sstream> 中: std::istringstream:输入流,从已有字符串中读取并解析。std::ostringstream:输出流,向内部缓冲区写入内容,最终取…...

OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别
OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别 直接训练提示词嵌入向量的核心区别 您提到的代码: prompt_embedding = initial_embedding.clone().requires_grad_(True) optimizer = torch.optim.Adam([prompt_embedding...

Rapidio门铃消息FIFO溢出机制
关于RapidIO门铃消息FIFO的溢出机制及其与中断抖动的关系,以下是深入解析: 门铃FIFO溢出的本质 在RapidIO系统中,门铃消息FIFO是硬件控制器内部的缓冲区,用于临时存储接收到的门铃消息(Doorbell Message)。…...
)
Android第十三次面试总结(四大 组件基础)
Activity生命周期和四大启动模式详解 一、Activity 生命周期 Activity 的生命周期由一系列回调方法组成,用于管理其创建、可见性、焦点和销毁过程。以下是核心方法及其调用时机: onCreate() 调用时机:Activity 首次创建时调用。…...

初探Service服务发现机制
1.Service简介 Service是将运行在一组Pod上的应用程序发布为网络服务的抽象方法。 主要功能:服务发现和负载均衡。 Service类型的包括ClusterIP类型、NodePort类型、LoadBalancer类型、ExternalName类型 2.Endpoints简介 Endpoints是一种Kubernetes资源…...

AI+无人机如何守护濒危物种?YOLOv8实现95%精准识别
【导读】 野生动物监测在理解和保护生态系统中发挥着至关重要的作用。然而,传统的野生动物观察方法往往耗时耗力、成本高昂且范围有限。无人机的出现为野生动物监测提供了有前景的替代方案,能够实现大范围覆盖并远程采集数据。尽管具备这些优势…...

作为测试我们应该关注redis哪些方面
1、功能测试 数据结构操作:验证字符串、列表、哈希、集合和有序的基本操作是否正确 持久化:测试aof和aof持久化机制,确保数据在开启后正确恢复。 事务:检查事务的原子性和回滚机制。 发布订阅:确保消息正确传递。 2、性…...
