每天一道leetcode:1129. 颜色交替的最短路径(图论中等广度优先遍历)
今日份题目:
给定一个整数 n,即有向图中的节点数,其中节点标记为 0 到 n - 1。图中的每条边为红色或者蓝色,并且可能存在自环或平行边。
给定两个数组 redEdges 和 blueEdges,其中:
-
redEdges[i] = [ai, bi]表示图中存在一条从节点ai到节点bi的红色有向边, -
blueEdges[j] = [uj, vj]表示图中存在一条从节点uj到节点vj的蓝色有向边。
返回长度为 n 的数组 answer,其中 answer[X] 是从节点 0 到节点 X 的红色边和蓝色边交替出现的最短路径的长度。如果不存在这样的路径,那么 answer[x] = -1。
示例1
输入:n = 3, red_edges = [[0,1],[1,2]], blue_edges = [] 输出:[0,1,-1]
示例2
输入:n = 3, red_edges = [[0,1]], blue_edges = [[2,1]] 输出:[0,1,-1]
提示
-
1 <= n <= 100 -
0 <= redEdges.length, blueEdges.length <= 400 -
redEdges[i].length == blueEdges[j].length == 2 -
0 <= ai, bi, uj, vj < n
题目思路
依旧是使用bfs广度优先遍历,详细过程可看代码中的注释。
本道题目主要是注意细节,比如三维表next、二维表dist等等。
代码
class Solution
{
public:vector<int> shortestAlternatingPaths(int n, vector<vector<int>>& redEdges, vector<vector<int>>& blueEdges) {vector<vector<vector<int> > > next(2,vector<vector<int> >(n));for(auto &e:redEdges) {next[0][e[0]].push_back(e[1]);//第一个二维表存放红边信息}for(auto &e:blueEdges) {next[1][e[0]].push_back(e[1]);//第二个二维表存放蓝边信息}vector<vector<int> > dist(2,vector<int>(n,INT_MAX)); //两种类型的颜色最短路径的长度queue<pair<int, int> > p;dist[0][0]=0;dist[1][0]=0;p.push({0,0});//第一个表的0p.push({0,1});//第二个表的0while(!p.empty()) {int xy=p.front();p.pop();for(auto y:next[1-xy.second][xy.first]) //遍历当前点的邻接点{if(dist[1-xy.second][y]!=INT_MAX) //表示遍历过了{continue;}//实现交替路径dist[1-xy.second][y]=dist[xy.second][xy.first]+1;//另一个颜色的边数加一p.push({y,1-xy.second});}}vector<int> ans(n);for(int i=0;i<n;i++) {ans[i]=min(dist[0][i],dist[1][i]);//两个图中最小的路径长if(ans[i]==INT_MAX) //不存在,置为-1{ans[i]=-1;}}return ans;}
};
提交结果
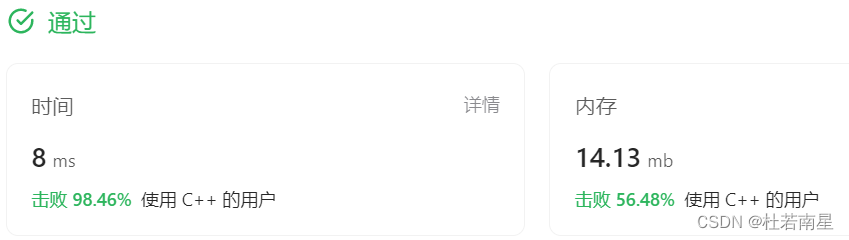
欢迎大家在评论区讨论,如有不懂的代码部分,欢迎在评论区留言!
相关文章:

每天一道leetcode:1129. 颜色交替的最短路径(图论中等广度优先遍历)
今日份题目: 给定一个整数 n,即有向图中的节点数,其中节点标记为 0 到 n - 1。图中的每条边为红色或者蓝色,并且可能存在自环或平行边。 给定两个数组 redEdges 和 blueEdges,其中: redEdges[i] [ai, bi…...
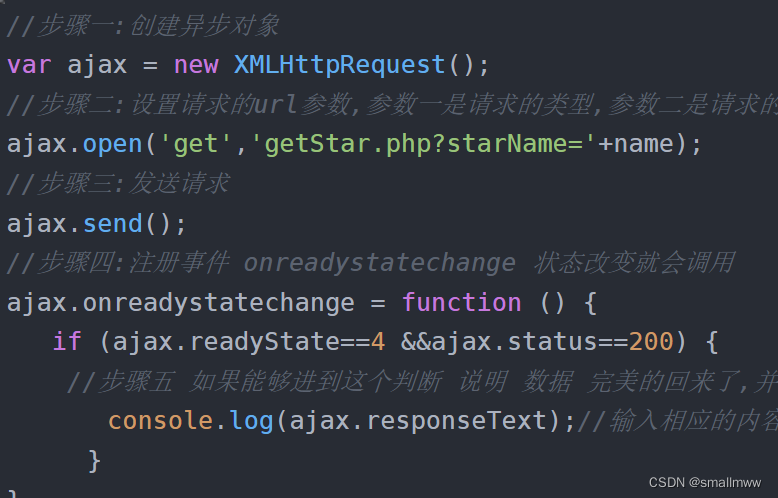
原生js发送ajax请求---ajax请求篇(一)
在原生js中我们使用的是XMLHttpRequest对象来发送ajax请求 主要步骤就是: 1.创建XMLHTTPRequest对象 2.使用open方法设置和服务器的交互信息 3.设置发送的数据,开始和服务器端交互 4.注册事件 5.更新界面 (1) get方式 //步骤一…...

【ARM 嵌入式 编译系列 2.1 -- GCC 编译参数学习】
文章目录 1.1 GCC 编译参数1.1.1 GCC arm-noe-eabi- 介绍1.1.1.1 ARM 和 Thumb 指令集区别1.1.2 GCC CFLAGS 介绍1.1.3 GCC LDFLAGS 介绍1.1.4 CXXFLAGS 介绍上篇文章:ARM 嵌入式 编译系列 2 – GCC 编译过程介绍 下篇文章:ARM 嵌入式 C 入门及渐进 3 – GCC attribute((weak…...

C++教程 - How to C++系列专栏第3篇
关于专栏 这个专栏是优质的C教程专栏,如果你还没看过第0篇,点击C教程 - How to C系列专栏第0篇去第0篇 本专栏一致使用操作系统:macOS Ventura,代码编辑器:CLion,C编译器:Clang 感谢一路相伴…...
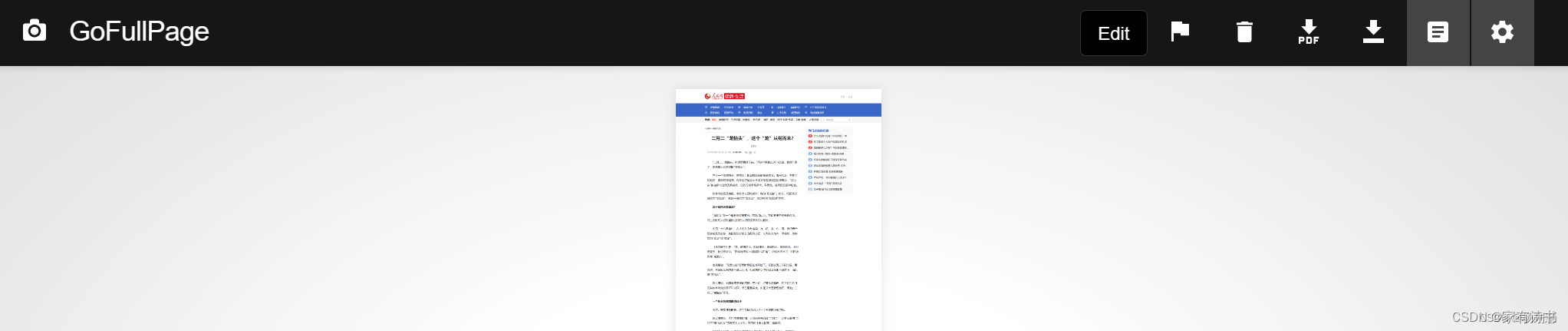
使用Edge和chrom扩展工具(GoFullPage)实现整页面截图或生成PDF文件
插件GoFullPage下载:点击免费下载 如果在浏览网页时,有需要整个页面截图或导出PDF文件的需求,这里分享一个Edge浏览器的扩展插件:GoFullPage。 这个工具可以一键实现页面从上到下滚动并截取。 一、打开“管理扩展”(…...

image has dependent child images
问题:很多none的镜像无法被删除 解决过程: 1、通过 docker image prune -f 提示可删除为 0 2、直接进行删除报错: docker rmi 8f5116cbc201Error response from daemon: conflict: unable to delete 8f5116cbc201 (cannot be forced) - im…...

Linux系统中基于NGINX的代理缓存配置指南
作为一名专业的爬虫程序员,你一定知道代理缓存在加速网站响应速度方面的重要性。而使用NGINX作为代理缓存服务器,能够极大地提高性能和效率。本文将为你分享Linux系统中基于NGINX的代理缓存配置指南,提供实用的解决方案,助你解决在…...
)
openCV项目开发实战--详细介绍如何改善夜间图像的照明(附python和C++源码)
文末附完整的代码实现下载链接 介绍 对于非摄影师来说,在光线不佳的条件下拍出好照片似乎很神奇。完成低光摄影需要技巧、经验和正确的设备的结合。在弱光下拍摄的图像缺乏色彩和独特的边缘。它们还遭受能见度差和深度未知的困扰。这些缺点使得此类图像不适合个人使用或图像处…...

rabbitmq的消息应答
消费者完成一个任务可能需要一段时间,如果其中一个消费者处理一个长的任务并仅只完成 了部分突然它挂掉了,会发生什么情况。RabbitMQ 一旦向消费者传递了一条消息,便立即将该消 息标记为删除。在这种情况下,突然有个消费者挂掉了…...
)
如何重置树莓派 Pico(重置外围设备失败)
有时候需要重置树莓派 Pico,一种方法是按住 Pico 上的“BOOTSEL”按钮再插入 USB;或者用按钮连接“RUN”和“GND”针脚,然后同时按下这个按钮和“BOOTSEL”按钮。这样就可以进入 USB 模式,这样从一定程度进行了重置。 但是这种方…...

LaWGPT基于中文法律知识的大语言模型_初步安装
准备代码,创建环境 # 下载代码 git clone gitgithub.com:pengxiao-song/LaWGPT.git cd LaWGPT# 创建环境 conda create -n lawgpt python3.10 -y conda activate lawgpt国内网络环境问题。你可以把requirements.txt里面的github.com替换成kgithub.com(这…...

一文学会sklearn中的交叉验证方法,cross_validate和KFlod实战案例
前言 在机器学习中,我们经常需要评估模型的性能。而为了准确评估模型的性能,我们需要使用一种有效的评估方法。五折交叉验证(5-fold cross-validation)就是其中一种常用的模型评估方法,用于评估机器学习模型的性能和泛…...

《面试1v1》ElasticSearch倒排索引
🍅 作者简介:王哥,CSDN2022博客总榜Top100🏆、博客专家💪 🍅 技术交流:定期更新Java硬核干货,不定期送书活动 🍅 王哥多年工作总结:Java学习路线总结…...
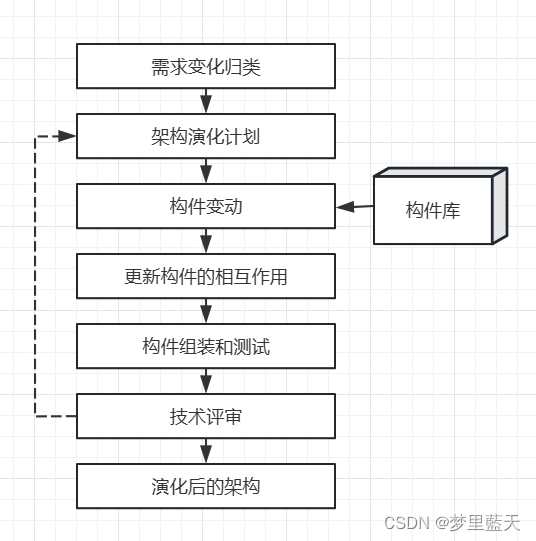
基于架构的软件开发方法
基于架构的软件开发方法 基于架构的软件开发方法是由架构驱动的,即指由构成体系结构的商业、质量和功能需求的组合驱动的。使用ABSD 方法,设计活动可以从项目总体功能框架明确就开始,这意味着需求抽取和分析还没有完成(甚至远远没有完成)&am…...
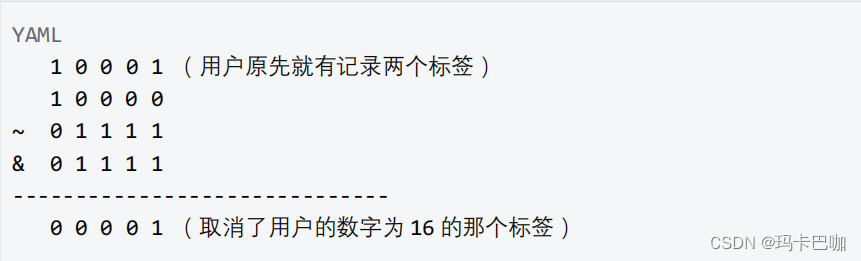
实战篇之基于二进制思想的用户标签系统(Mysql+SpringBoot)
一: 计算机中的二进制 计算机以二进制表示数据,以表示电路中的正反。在二进制下,一个位只有 0 和 1 。逢二进一 位。类似十进制下,一个位只有 0~9 。逢十进一位。 二: 进制常用运算 (位运算)…...

Ansible 进阶
Ansible 进阶 ⤴️Ansible 入门看这篇文章⤵️Ansible 实战看这篇文章 一.Ansible 中的 Playbook 1.1 Playbook 介绍 如下图,ansible 在整个管理过程中使用 playbook 的大体流程。 Playbook 中包含多个 role,每个 role 对应于在远程主机完成某个比较复…...

滴滴Ceph分布式存储系统优化之锁优化
摘自:https://mp.weixin.qq.com/s/oWujGOLLGItu1Bv5AuO0-A 2020-09-02 21:45 0.引言 Ceph是国际知名的开源分布式存储系统,在工业界和学术界都有着重要的影响。Ceph的架构和算法设计发表在国际系统领域顶级会议OSDI、SOSP、SC等上。Ceph社区得到Red Hat…...

flutter开发实战-MethodChannel实现flutter与iOS双向通信
flutter开发实战-MethodChannel实现flutter与iOS双向通信 最近开发中需要iOS与flutter实现通信,这里使用的MethodChannel 如果需要flutter与Android实现双向通信,请看 https://blog.csdn.net/gloryFlow/article/details/132218837 这部分与https://bl…...
)
华为、阿里巴巴、字节跳动 100+ Python 面试问题总结(七)
系列文章目录 个人简介:机电专业在读研究生,CSDN内容合伙人,博主个人首页 Python面试专栏:《Python面试》此专栏面向准备面试的2024届毕业生。欢迎阅读,一起进步!🌟🌟🌟 …...
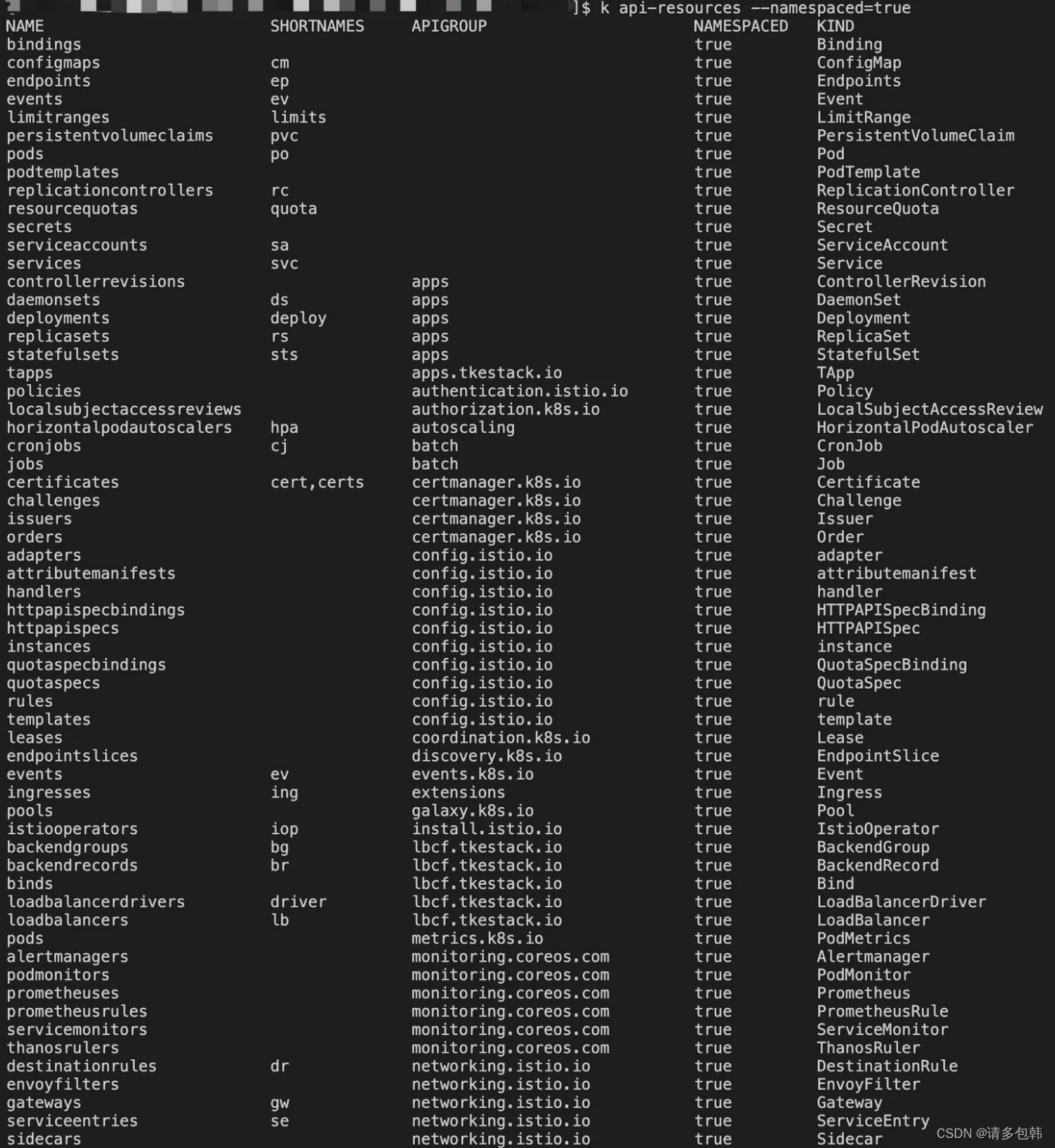
K8S系列一:概念入门
写在前面 本文组织方式: K8S的架构、作用和目的。需要首先对K8S整体有所了解。 K8S是什么? 为什么是K8S? K8S怎么做? K8S的重要概念,即K8S的API对象。要学习和使用K8S必须知道和掌握的几个对象。 Pod 实例 Volume 数…...

华为云AI开发平台ModelArts
华为云ModelArts:重塑AI开发流程的“智能引擎”与“创新加速器”! 在人工智能浪潮席卷全球的2025年,企业拥抱AI的意愿空前高涨,但技术门槛高、流程复杂、资源投入巨大的现实,却让许多创新构想止步于实验室。数据科学家…...

Docker 离线安装指南
参考文章 1、确认操作系统类型及内核版本 Docker依赖于Linux内核的一些特性,不同版本的Docker对内核版本有不同要求。例如,Docker 17.06及之后的版本通常需要Linux内核3.10及以上版本,Docker17.09及更高版本对应Linux内核4.9.x及更高版本。…...

<6>-MySQL表的增删查改
目录 一,create(创建表) 二,retrieve(查询表) 1,select列 2,where条件 三,update(更新表) 四,delete(删除表…...

简易版抽奖活动的设计技术方案
1.前言 本技术方案旨在设计一套完整且可靠的抽奖活动逻辑,确保抽奖活动能够公平、公正、公开地进行,同时满足高并发访问、数据安全存储与高效处理等需求,为用户提供流畅的抽奖体验,助力业务顺利开展。本方案将涵盖抽奖活动的整体架构设计、核心流程逻辑、关键功能实现以及…...

【HarmonyOS 5.0】DevEco Testing:鸿蒙应用质量保障的终极武器
——全方位测试解决方案与代码实战 一、工具定位与核心能力 DevEco Testing是HarmonyOS官方推出的一体化测试平台,覆盖应用全生命周期测试需求,主要提供五大核心能力: 测试类型检测目标关键指标功能体验基…...

基于Uniapp开发HarmonyOS 5.0旅游应用技术实践
一、技术选型背景 1.跨平台优势 Uniapp采用Vue.js框架,支持"一次开发,多端部署",可同步生成HarmonyOS、iOS、Android等多平台应用。 2.鸿蒙特性融合 HarmonyOS 5.0的分布式能力与原子化服务,为旅游应用带来…...

Frozen-Flask :将 Flask 应用“冻结”为静态文件
Frozen-Flask 是一个用于将 Flask 应用“冻结”为静态文件的 Python 扩展。它的核心用途是:将一个 Flask Web 应用生成成纯静态 HTML 文件,从而可以部署到静态网站托管服务上,如 GitHub Pages、Netlify 或任何支持静态文件的网站服务器。 &am…...

CocosCreator 之 JavaScript/TypeScript和Java的相互交互
引擎版本: 3.8.1 语言: JavaScript/TypeScript、C、Java 环境:Window 参考:Java原生反射机制 您好,我是鹤九日! 回顾 在上篇文章中:CocosCreator Android项目接入UnityAds 广告SDK。 我们简单讲…...

《基于Apache Flink的流处理》笔记
思维导图 1-3 章 4-7章 8-11 章 参考资料 源码: https://github.com/streaming-with-flink 博客 https://flink.apache.org/bloghttps://www.ververica.com/blog 聚会及会议 https://flink-forward.orghttps://www.meetup.com/topics/apache-flink https://n…...

蓝桥杯3498 01串的熵
问题描述 对于一个长度为 23333333的 01 串, 如果其信息熵为 11625907.5798, 且 0 出现次数比 1 少, 那么这个 01 串中 0 出现了多少次? #include<iostream> #include<cmath> using namespace std;int n 23333333;int main() {//枚举 0 出现的次数//因…...
