Floyd算法
正如我们所知道的,Floyd算法用于求最短路径。Floyd算法可以说是Warshall算法的扩展,三个for循环就可以解决问题,所以它的时间复杂度为O(n^3)。
Floyd算法的基本思想如下:从任意节点A到任意节点B的最短路径不外乎2种可能,1是直接从A到B,2是从A经过若干个节点X到B。所以,我们假设Dis(AB)为节点A到节点B的最短路径的距离,对于每一个节点X,我们检查Dis(AX) + Dis(XB) < Dis(AB)是否成立,如果成立,证明从A到X再到B的路径比A直接到B的路径短,我们便设置Dis(AB) = Dis(AX) + Dis(XB),这样一来,当我们遍历完所有节点X,Dis(AB)中记录的便是A到B的最短路径的距离。
很简单吧,代码看起来可能像下面这样:
for ( int i = 0; i < 节点个数; ++i ){for ( int j = 0; j < 节点个数; ++j ){for ( int k = 0; k < 节点个数; ++k ){if ( Dis[i][k] + Dis[k][j] < Dis[i][j] ){// 找到更短路径Dis[i][j] = Dis[i][k] + Dis[k][j];}}}}但是这里我们要注意循环的嵌套顺序,如果把检查所有节点X放在最内层,那么结果将是不正确的,为什么呢?因为这样便过早的把i到j的最短路径确定下来了,而当后面存在更短的路径时,已经不再会更新了。
让我们来看一个例子,看下图:
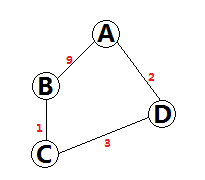
图中红色的数字代表边的权重。如果我们在最内层检查所有节点X,那么对于A->B,我们只能发现一条路径,就是A->B,路径距离为9。而这显然是不正确的,真实的最短路径是A->D->C->B,路径距离为6。造成错误的原因就是我们把检查所有节点X放在最内层,造成过早的把A到B的最短路径确定下来了,当确定A->B的最短路径时Dis(AC)尚未被计算。所以,我们需要改写循环顺序,如下:
for ( int k = 0; k < 节点个数; ++k ){for ( int i = 0; i < 节点个数; ++i ){for ( int j = 0; j < 节点个数; ++j ){if ( Dis[i][k] + Dis[k][j] < Dis[i][j] ){// 找到更短路径Dis[i][j] = Dis[i][k] + Dis[k][j];}}}}这样一来,对于每一个节点X,我们都会把所有的i到j处理完毕后才继续检查下一个节点。
那么接下来的问题就是,我们如何找出最短路径呢?这里需要借助一个辅助数组Path,它是这样使用的:Path(AB)的值如果为P,则表示A节点到B节点的最短路径是A->...->P->B。这样一来,假设我们要找A->B的最短路径,那么就依次查找,假设Path(AB)的值为P,那么接着查找Path(AP),假设Path(AP)的值为L,那么接着查找Path(AL),假设Path(AL)的值为A,则查找结束,最短路径为A->L->P->B。
那么,如何填充Path的值呢?很简单,当我们发现Dis(AX) + Dis(XB) < Dis(AB)成立时,就要把最短路径改为A->...->X->...->B,而此时,Path(XB)的值是已知的,所以,Path(AB) = Path(XB)。
好了,基本的介绍完成了,接下来就是实现的时候了,这里我们使用图以及邻接矩阵:
#define INFINITE 1000 // 最大值#define MAX_VERTEX_COUNT 20 // 最大顶点个数//struct Graph{int arrArcs[MAX_VERTEX_COUNT][MAX_VERTEX_COUNT]; // 邻接矩阵int nVertexCount; // 顶点数量int nArcCount; // 边的数量};//首先,我们写一个方法,用于读入图的数据:
void readGraphData( Graph *_pGraph ){std::cout << "请输入顶点数量和边的数量: ";std::cin >> _pGraph->nVertexCount;std::cin >> _pGraph->nArcCount;std::cout << "请输入邻接矩阵数据:" << std::endl;for ( int row = 0; row < _pGraph->nVertexCount; ++row ){for ( int col = 0; col < _pGraph->nVertexCount; ++col ){std::cin >> _pGraph->arrArcs[row][col];}}}接着,就是核心的Floyd算法:
void floyd( int _arrDis[][MAX_VERTEX_COUNT], int _arrPath[][MAX_VERTEX_COUNT], int _nVertexCount ){// 先初始化_arrPathfor ( int i = 0; i < _nVertexCount; ++i ){for ( int j = 0; j < _nVertexCount; ++j ){_arrPath[i][j] = i;}}//for ( int k = 0; k < _nVertexCount; ++k ){for ( int i = 0; i < _nVertexCount; ++i ){for ( int j = 0; j < _nVertexCount; ++j ){if ( _arrDis[i][k] + _arrDis[k][j] < _arrDis[i][j] ){// 找到更短路径_arrDis[i][j] = _arrDis[i][k] + _arrDis[k][j];_arrPath[i][j] = _arrPath[k][j];}}}}}OK,最后是输出结果数据代码:
void printResult( int _arrDis[][MAX_VERTEX_COUNT], int _arrPath[][MAX_VERTEX_COUNT], int _nVertexCount ){std::cout << "Origin -> Dest Distance Path" << std::endl;for ( int i = 0; i < _nVertexCount; ++i ){for ( int j = 0; j < _nVertexCount; ++j ){if ( i != j ) // 节点不是自身{std::cout << i+1 << " -> " << j+1 << "\t\t";if ( INFINITE == _arrDis[i][j] ) // i -> j 不存在路径{std::cout << "INFINITE" << "\t\t";}else{std::cout << _arrDis[i][j] << "\t\t";// 由于我们查询最短路径是从后往前插,因此我们把查询得到的节点// 压入栈中,最后弹出以顺序输出结果。std::stack<int> stackVertices;int k = j;do{k = _arrPath[i][k];stackVertices.push( k );} while ( k != i );//std::cout << stackVertices.top()+1;stackVertices.pop();unsigned int nLength = stackVertices.size();for ( unsigned int nIndex = 0; nIndex < nLength; ++nIndex ){std::cout << " -> " << stackVertices.top()+1;stackVertices.pop();}std::cout << " -> " << j+1 << std::endl;}}}}}好了,是时候测试了,我们用的图如下:
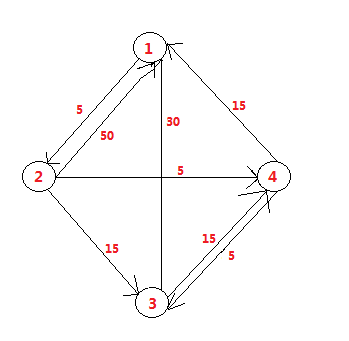
测试代码如下:
int main( void ){Graph myGraph;readGraphData( &myGraph );//int arrDis[MAX_VERTEX_COUNT][MAX_VERTEX_COUNT];int arrPath[MAX_VERTEX_COUNT][MAX_VERTEX_COUNT];// 先初始化arrDisfor ( int i = 0; i < myGraph.nVertexCount; ++i ){for ( int j = 0; j < myGraph.nVertexCount; ++j ){arrDis[i][j] = myGraph.arrArcs[i][j];}}floyd( arrDis, arrPath, myGraph.nVertexCount );//printResult( arrDis, arrPath, myGraph.nVertexCount );//system( "pause" );return 0;}如图:
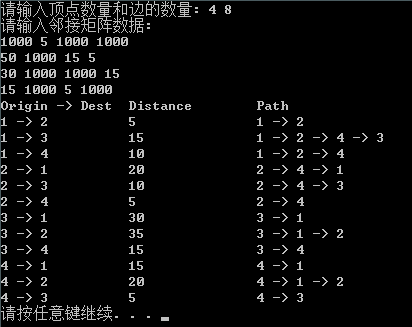
相关文章:

Floyd算法
正如我们所知道的,Floyd算法用于求最短路径。Floyd算法可以说是Warshall算法的扩展,三个for循环就可以解决问题,所以它的时间复杂度为O(n^3)。 Floyd算法的基本思想如下:从任意节点A到任意节点B的最短路径不外乎2种可能ÿ…...

SpringBoot究竟应该如何学习?
如果你有Spring的基础,学习Spring Boot就很简单了。 首先要知道Spring Boot是建立在Spring框架之上的,它旨在简化和加速Java应用程序的开发过程。 Spring Boot的目标是简化Spring应用程序的配置和开发,通过提供自动配置、快速开发和零配置的…...

为什么很多人认为ChatGPT最好的替代工具是Claude?
ChatGPT引领着生成式AI聊天机器人领域,但Claude AI看起来是一个有力的竞争者。 前段时间,ChatGPT的强劲竞争对手Claude2面世。当时很多人认为它可能会取代ChatGPT,在体验过一段时间之后,深以为然。原因如下: 更强大的…...

学习Vue:简介和优势
什么是 Vue.js? Vue.js 是一个用于构建用户界面的渐进式 JavaScript 框架。它专注于视图层,并且可以轻松地集成到现有的项目中。Vue.js 的设计理念是渐进式,这意味着您可以根据项目的需要逐步引入 Vue.js,从而更好地控制应用的复…...

***is not a commit and a branch ‘***‘ cannot be created from it 报错
git执行如下代码 git checkout -b daily/1.0.0 origin/daily/1.0.0遇到报错 fatal: ‘origin/daily/1.0.27’ is not a commit and a branch ‘daily/1.0.27’ cannot be created from it 解决办法: git fetch --all原因: 报错说is not a commit而不是说branch doesn’t exis…...

QT信号槽连接方式
1.QT信号槽主要分两个连接方式,手动和自动: 1.1 使用 connect() 函数手动连接信号和槽: QObject::connect(sender, SIGNAL(signal()), receiver, SLOT(slot())); 自动: 1.2 使用 lambda 表达式连接信号和槽: connect(s…...
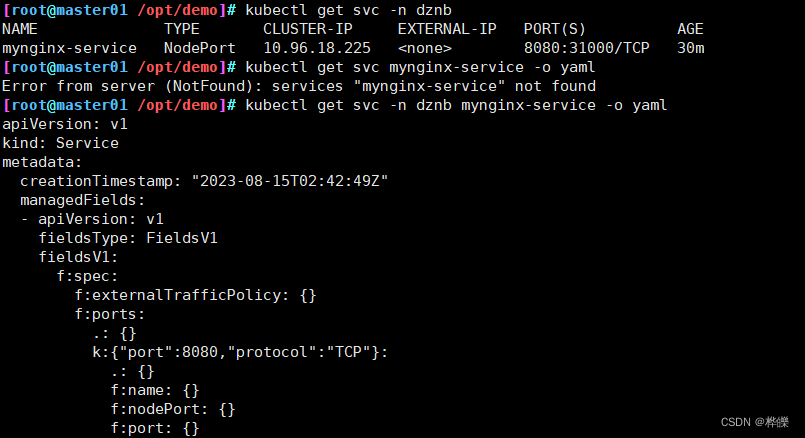
【yml文件的解释】
目录 一、yml的简介二、手写yml文件进行配置三、使用yaml格式导出生成模板四、deployment.yaml文件详解五、Pod yaml文件详解六、Service yaml文件详解 一、yml的简介 Kubernetes 支持 YAML 和 JSON 格式管理资源对象 JSON 格式:主要用于 api 接口之间消息的传递 Y…...
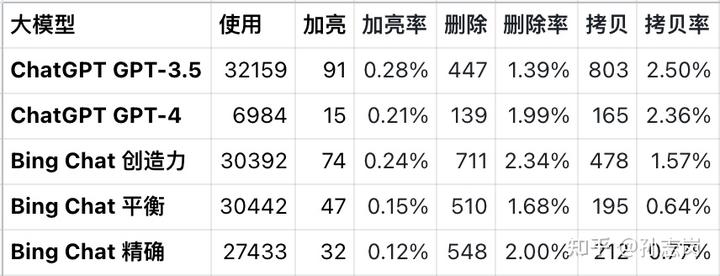
ChatGPT or BingChat
你相信我们对大模型也存在「迷信权威」吗? ChatGPT 的 GPT-4 名声在外,我们就不自觉地更相信它,优先使用它。但我用 ChatALL 比较 AI 大模型们这么久,得到的结论是: ChatGPT GPT-4 在大多数情况下确实是最强…...

QT 使用第三方库QtXlsx操作Excel表
1.简介 一直以来,都想学习一下C/C如何操作excel表,在网上调研了一下,觉得使用C/C去操作很麻烦,遂转向QT这边;QT有一个自带的类QAxObject,可以使用他去操作,但随着了解的深入,觉得他…...

警惕网络个人技术人员:隐藏代码风险的启示
在当今数字化时代,我们对网络上个人技术人员的需求日益增加,这使得技术服务成为一项不可或缺的资源。然而,我最近的经历却引发了我对这种服务可靠性的怀疑,特别是当这些个人技术人员没有正式公司背景,缺乏可信的运营保…...
VBA 学习笔记1 对象以及属性
目录 1 取得VBA对象1.1 取得工作簿对象1.2 取得工作表对象1.3 取得单元格对象1.4 取得对象的属性1.5 文档的方法1 进入vba 界面 方式之一: 快捷键:ALTERF11 运行方式之一: 进入vba界面,点击绿色三角符号 1 取得VBA对象 1.1 取得…...

netty核心组件以及实现原理
Netty核心组件 网络通信层:这一层有三个核心组件:Bootstrap、ServerBootStrap和Channel。Bootstrap负责客户端的启动,并用来链接远程Netty Server;ServerBootStrap负责服务端监听,用来监听指定端口;Channe…...
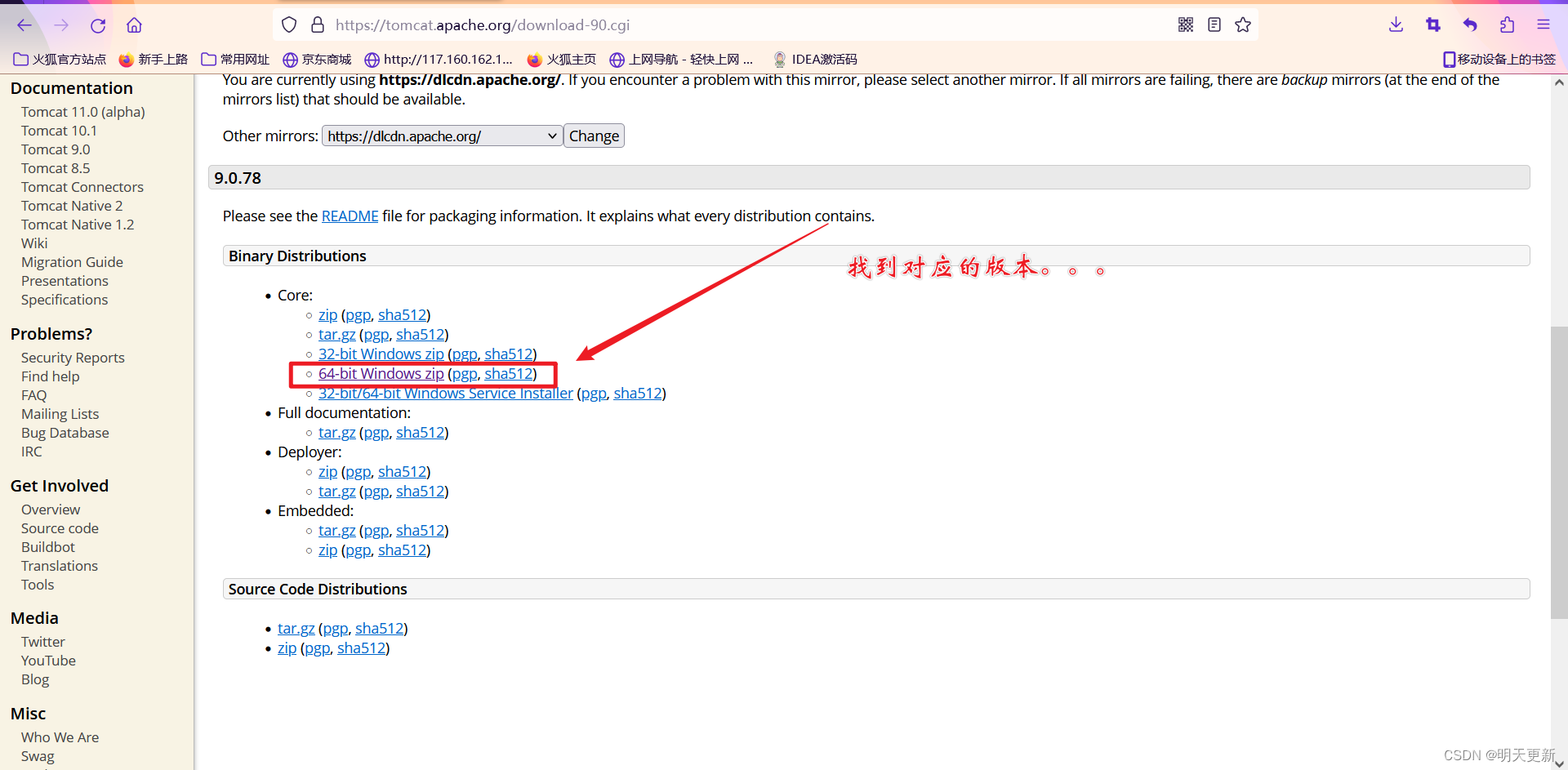
如何正确下载tomcat???
亲爱的小伙伴,千万别再去找下网站下载啦,这样詪容易携带病毒。 我们去官方网址下载。 Apache Tomcat - Welcome! 最后下载解压即可。。。...
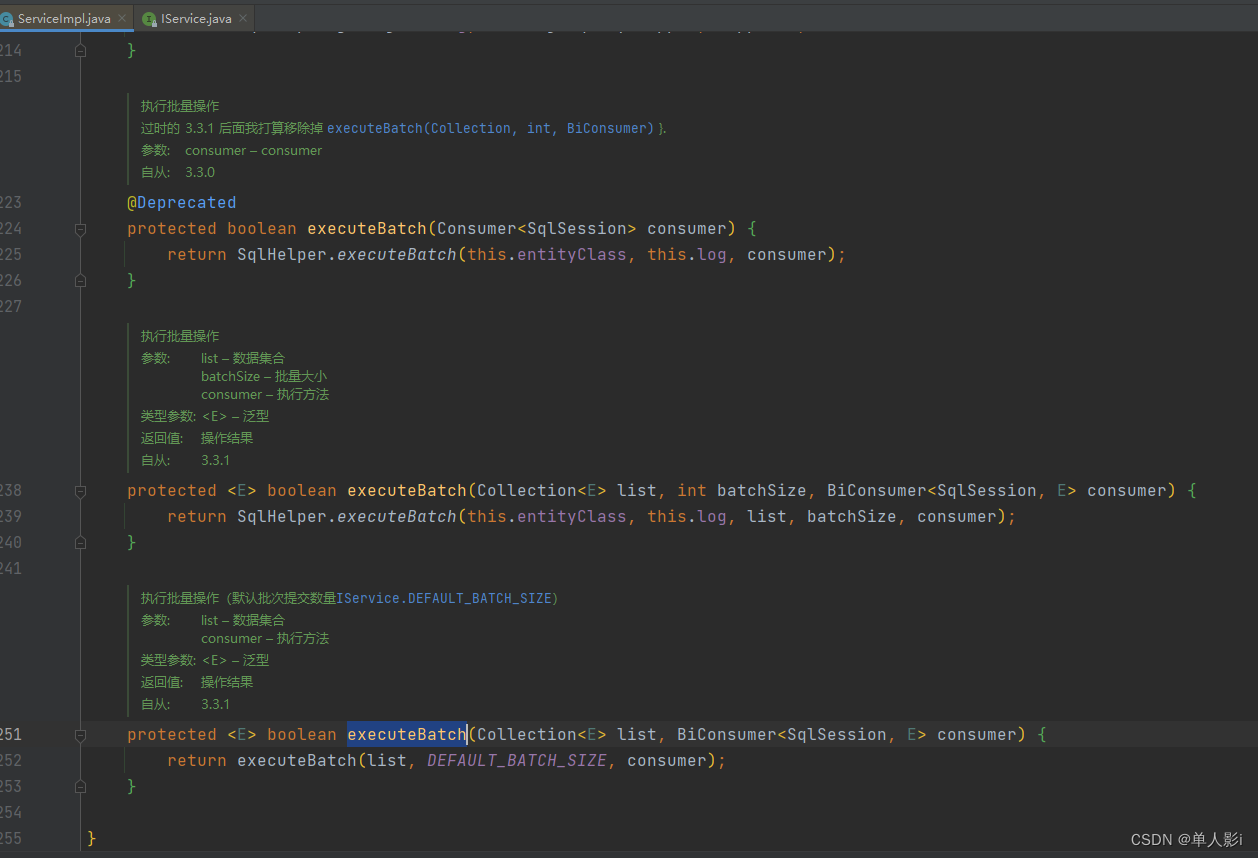
mybatis-plus 根据指定字段 批量 删除/修改
mybatis-plus 提供了根据id批量更新和修改的方法,这个大家都不陌生 但是当表没有id的时候怎么办 方案一: 手写SQL方案二: 手动获取SqlSessionTemplate 就是把mybatis plus 干的事自己干了方案三 : 重写 executeBatch 方法结论: mybatis-plus 提供了根据id批量更新和修改的方法,…...

MQTT宝典
文章目录 1.介绍2.发布和订阅3.MQTT 数据包结构4.Demo5.EMQX 1.介绍 什么是MQTT协议 MQTT(消息队列遥测传输协议),是一种基于发布/订阅(publish/subscribe)模式的“轻量级”通讯协议,该协议构建于TCP/IP协…...
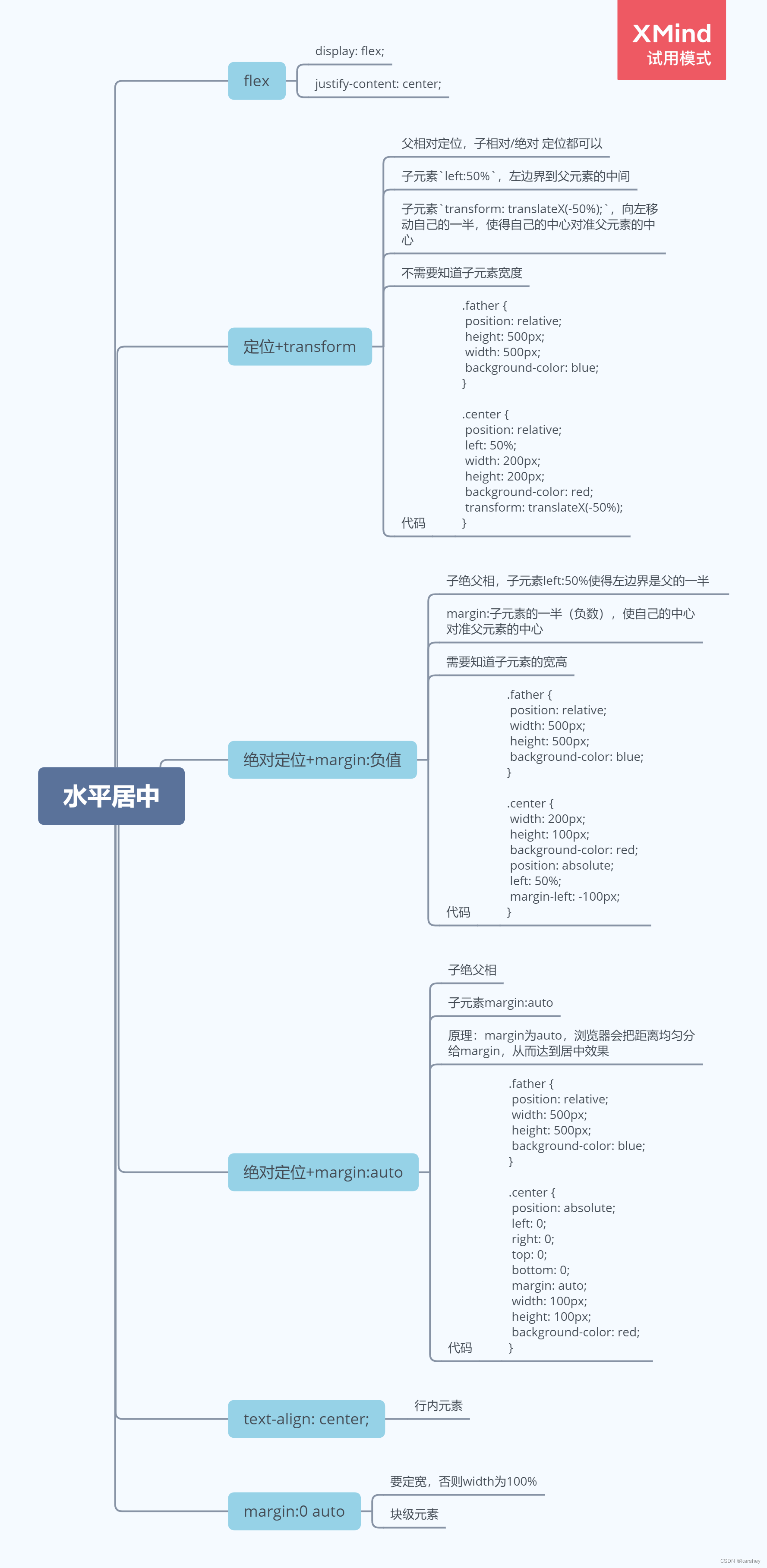
【前端】CSS水平居中的6种方法
文章目录 flex绝对定位margin:auto绝对定位margin:负值定位transformtext-align: center;margin: 0 auto;思维导图 后文:【前端】CSS垂直居中的7种方法_karshey的博客-CSDN博客 左右两边间隔相等的居中 flex display: flex;justify-content: center; <div clas…...

nginx如何获取真实的ip
我这里使用是springboot项目,使用nginx做代理,但header里面的参数没有将ip带过来,所有需要配置nginx将ip带过来。 nginx.conf文件 server {listen 80;listen 443 ssl;server_name xxx.xxx.com;ssl_certificate /web/project/ai…...

kotlin + LiveData 测试
viewModel测试:https://developer.android.com/codelabs/basic-android-kotlin-compose-test-viewmodel#3 androidTestImplementation "org.jetbrains.kotlin:kotlin-test:1.9.0"androidTestImplementation org.jetbrains.kotlinx:kotlinx-coroutines-tes…...
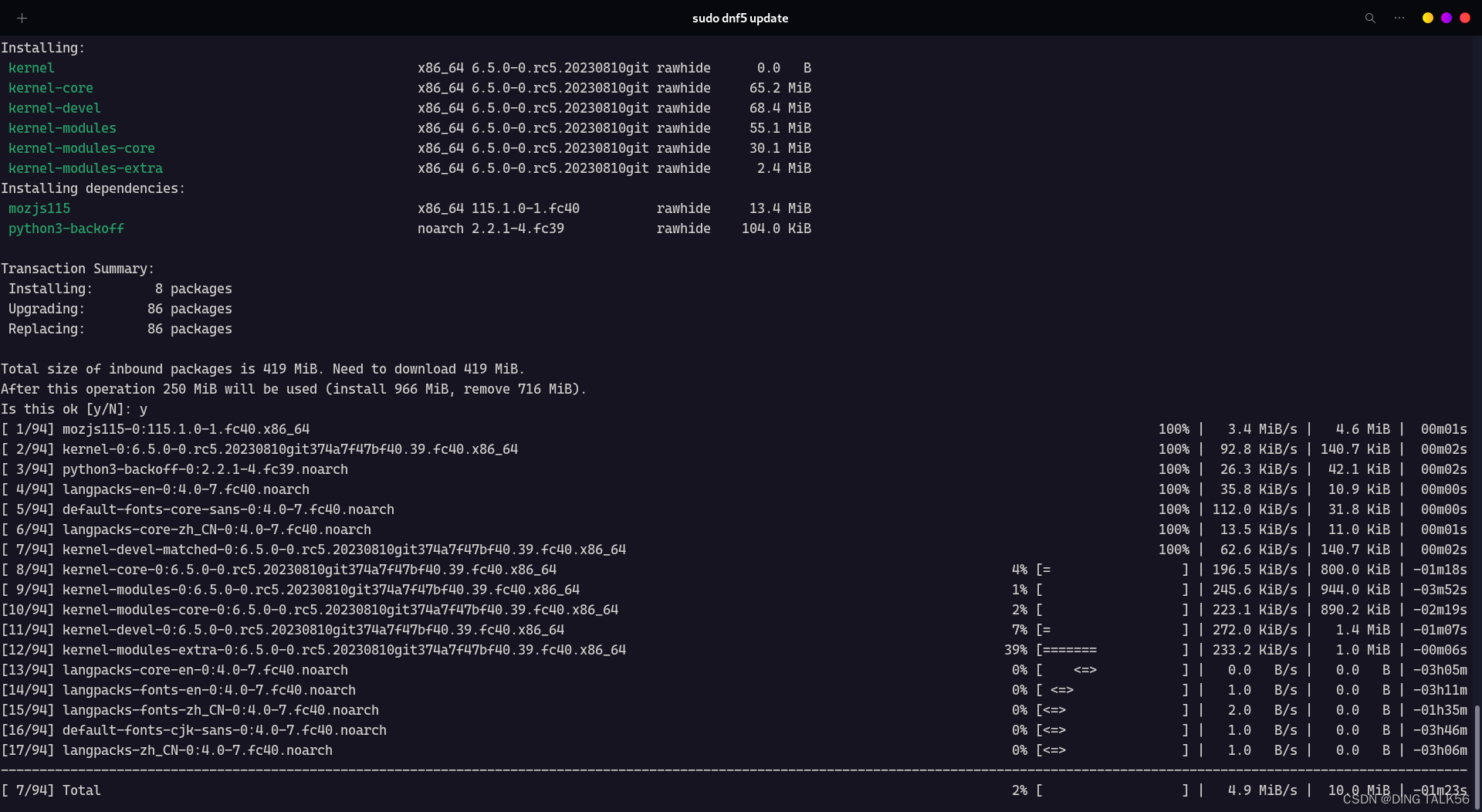
【dnf5文档】新一代RedHat自动化包管理器
前言 HI,CSDN的码友们,距离上一次我发文章已经过去了半年的时间,现在我又来介绍自己新发现和探究的开源技术了。计算机的发展总是飞速的,当我在写这篇文章的时候,Fedora rawhide已经进入了40版本、默认采用的自动化包管理器为dnf…...

数据可视化工具的三大类报表制作流程分享
电脑(pc)、移动、大屏三大类型的BI数据可视化报表制作步骤基本相同,差别就在于尺寸调整和具体的报表布局。这对于采用点击、拖拉拽方式来制作报表的奥威BI数据可视化工具来说就显得特别简单。接下来,我们就一起看看不这三大类型的…...

Python:操作 Excel 折叠
💖亲爱的技术爱好者们,热烈欢迎来到 Kant2048 的博客!我是 Thomas Kant,很开心能在CSDN上与你们相遇~💖 本博客的精华专栏: 【自动化测试】 【测试经验】 【人工智能】 【Python】 Python 操作 Excel 系列 读取单元格数据按行写入设置行高和列宽自动调整行高和列宽水平…...

Linux相关概念和易错知识点(42)(TCP的连接管理、可靠性、面临复杂网络的处理)
目录 1.TCP的连接管理机制(1)三次握手①握手过程②对握手过程的理解 (2)四次挥手(3)握手和挥手的触发(4)状态切换①挥手过程中状态的切换②握手过程中状态的切换 2.TCP的可靠性&…...

leetcodeSQL解题:3564. 季节性销售分析
leetcodeSQL解题:3564. 季节性销售分析 题目: 表:sales ---------------------- | Column Name | Type | ---------------------- | sale_id | int | | product_id | int | | sale_date | date | | quantity | int | | price | decimal | -…...

零基础设计模式——行为型模式 - 责任链模式
第四部分:行为型模式 - 责任链模式 (Chain of Responsibility Pattern) 欢迎来到行为型模式的学习!行为型模式关注对象之间的职责分配、算法封装和对象间的交互。我们将学习的第一个行为型模式是责任链模式。 核心思想:使多个对象都有机会处…...

Unit 1 深度强化学习简介
Deep RL Course ——Unit 1 Introduction 从理论和实践层面深入学习深度强化学习。学会使用知名的深度强化学习库,例如 Stable Baselines3、RL Baselines3 Zoo、Sample Factory 和 CleanRL。在独特的环境中训练智能体,比如 SnowballFight、Huggy the Do…...

CSS | transition 和 transform的用处和区别
省流总结: transform用于变换/变形,transition是动画控制器 transform 用来对元素进行变形,常见的操作如下,它是立即生效的样式变形属性。 旋转 rotate(角度deg)、平移 translateX(像素px)、缩放 scale(倍数)、倾斜 skewX(角度…...

人工智能--安全大模型训练计划:基于Fine-tuning + LLM Agent
安全大模型训练计划:基于Fine-tuning LLM Agent 1. 构建高质量安全数据集 目标:为安全大模型创建高质量、去偏、符合伦理的训练数据集,涵盖安全相关任务(如有害内容检测、隐私保护、道德推理等)。 1.1 数据收集 描…...

抽象类和接口(全)
一、抽象类 1.概念:如果⼀个类中没有包含⾜够的信息来描绘⼀个具体的对象,这样的类就是抽象类。 像是没有实际⼯作的⽅法,我们可以把它设计成⼀个抽象⽅法,包含抽象⽅法的类我们称为抽象类。 2.语法 在Java中,⼀个类如果被 abs…...

Unity VR/MR开发-VR开发与传统3D开发的差异
视频讲解链接:【XR马斯维】VR/MR开发与传统3D开发的差异【UnityVR/MR开发教程--入门】_哔哩哔哩_bilibili...

Vue3 PC端 UI组件库我更推荐Naive UI
一、Vue3生态现状与UI库选择的重要性 随着Vue3的稳定发布和Composition API的广泛采用,前端开发者面临着UI组件库的重新选择。一个好的UI库不仅能提升开发效率,还能确保项目的长期可维护性。本文将对比三大主流Vue3 UI库(Naive UI、Element …...
