TypeScript教程(三)变量声明
一、变量声明
变量是一种使用方便的占位符,用于引用计算机内存地址,可以将变量看做存储数据的容器
命名规则:
1.变量名称可以包含数字和字母
2.除了下划线_和美元$符号外,不能包含其他特殊字符,包括空格
3.变量名不能以数字开头
以下四种方式声明变量:
1.声明变量的类型及初始值:
var [变量名] : [类型] = 值;var uname:string = "SSS"2.声明变量的类型,但没有初始值,变量值会设置为undefined:
var [变量名] = [类型];var uname = string3.声明变量名和初始值,但不设置类型,该变量可以为任意类型
var [变量名] = 值;var uname = "SSS"4.声明变量没有设置类型和初始值,类型可以是任意类型,默认初始值为undefined:
var [变量名]var uname;示例:
ts:
var uname:string = "Runoob";
var score1:number = 50;
var score2:number = 42.50
var sum = score1 + score2
console.log("名字: "+uname)
console.log("第一个科目成绩: "+score1)
console.log("第二个科目成绩: "+score2)
console.log("总成绩: "+sum)注:变量不要使用name,否则会与DOM中的全局window对象下的name属性出现重名
js:
var uname = "Runoob";
var score1 = 50;
var score2 = 42.50;
var sum = score1 + score2;
console.log("名字: " + uname);
console.log("第一个科目成绩: " + score1);
console.log("第二个科目成绩: " + score2);
console.log("总成绩: " + sum);结果:
名字: Runoob
第一个科目成绩: 50
第二个科目成绩: 42.5
总成绩: 92.5二、类型断言(Type Assertion)
类型断言可以用来手动指定一个值的类型,即允许变量从一种类型改为另一种类型
语法格式:
<类型> 值或值 as 类型示例:
var str = '1'
var str2:number = <number> <any> str //str、str2 是 string 类型
console.log(str2)TypeScript是如何确定单个断言是否足够:
当S类型是T类型的子集,或者T类型是S类型的子集时,S能被成功断言为T,这是为了在进行类型断言时提供额外的安全性,完全毫无根据的断言是危险的,除非用any
此之所以不能被称为类型转换,是因为转换通常意味着某种运行时的支持,但是,类型断言是一个编译时语法,同时,也是一种为编译器提供关于如何分析代码的方法
以上代码编译后的结果:
var str = '1';
var str2 = str; //str、str2 是 string 类型
console.log(str2);三、类型推断
当类型没有给出时,TypeScript编译器利用类型推断来推断类型
如果由于缺乏声明而不能推断出类型,那么它的类型被视作默认的动态any类型
var num = 2; // 类型推断为 number
console.log("num 变量的值为 "+num);
num = "12"; // 编译错误
console.log(num);第一行代码声明了变量num并=设置初始值为2,注意变量声明没有指定类型,因此,程序使用类型推断来确定变量的数据类型,第一次赋值为2,num设置为number类型
第三行,当再次为变量设置字符串类型的值时,编译会错误,因为变量已经设置了number类型
error TS2322: Type '"12"' is not assignable to type 'number'.四、变量作用域
变量作用域指定了变量定义的位置
程序中变量的可用性由变量作用域决定
TypeScript有以下几种作用域:
1.全局作用域:全局变量定义在程序结构的外部,它可以在代码的任何位置使用
2.类作用域:这个变量也可以称为字段,类变量声明在一个类里头,但在类的方法外面,该变量可以通过类的对象来访问,类变量可以是静态的,静态的变量可以通过类名直接访问
3.局部作用域:局部变量,局部变量只能在声明他的一个代码块(方法)中使用
示例:
ts:
var global_num = 12 // 全局变量
class Numbers { num_val = 13; // 实例变量static sval = 10; // 静态变量storeNum():void { var local_num = 14; // 局部变量}
}
console.log("全局变量为: "+global_num)
console.log(Numbers.sval) // 静态变量
var obj = new Numbers();
console.log("实例变量: "+obj.num_val)js:
var global_num = 12; // 全局变量
var Numbers = /** @class */ (function () {function Numbers() {this.num_val = 13; // 实例变量}Numbers.prototype.storeNum = function () {var local_num = 14; // 局部变量};Numbers.sval = 10; // 静态变量return Numbers;
}());
console.log("全局变量为: " + global_num);
console.log(Numbers.sval); // 静态变量
var obj = new Numbers();
console.log("实例变量: " + obj.num_val);结果:
全局变量为: 12
10
实例变量: 13如果在方法外调用局部变量会报错:
error TS2322: Could not find symbol 'local_num'.相关文章:
变量声明)
TypeScript教程(三)变量声明
一、变量声明 变量是一种使用方便的占位符,用于引用计算机内存地址,可以将变量看做存储数据的容器 命名规则: 1.变量名称可以包含数字和字母 2.除了下划线_和美元$符号外,不能包含其他特殊字符,包括空格 3.变量名…...

【数据结构】堆的实现,堆排序以及TOP-K问题
目录 1.堆的概念及结构 2.堆的实现 2.1初始化堆 2.2销毁堆 2.3取堆顶元素 2.4返回堆的大小 2.5判断是否为空 2.6打印堆 2.7插入元素 2.8堆的向上调整 2.9弹出元素 2.10堆的向下调整 3. 建堆时间复杂度 4. 堆的应用 4.1 堆排序 4.2 TOP-K问题 1.堆的概念及结构 …...
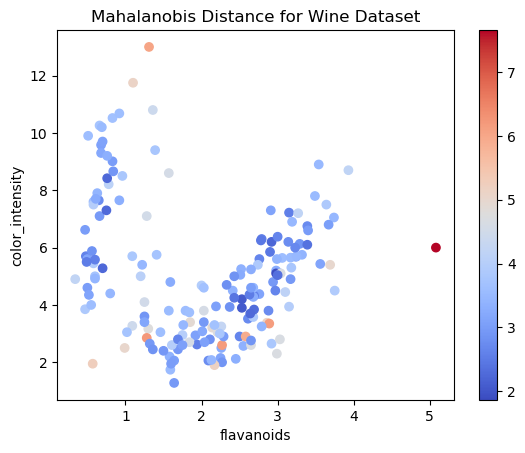
释放马氏距离的力量:用 Python 探索多元数据分析
一、说明 马哈拉诺比斯距离(Mahalanobis Distance)是一种测量两个概率分布之间距离的方法。它是基于样本协方差矩阵的函数,用于评估两个向量之间的相似程度。Mahalanobis Distance考虑了数据集中各个特征之间的协方差,因此比欧氏距…...
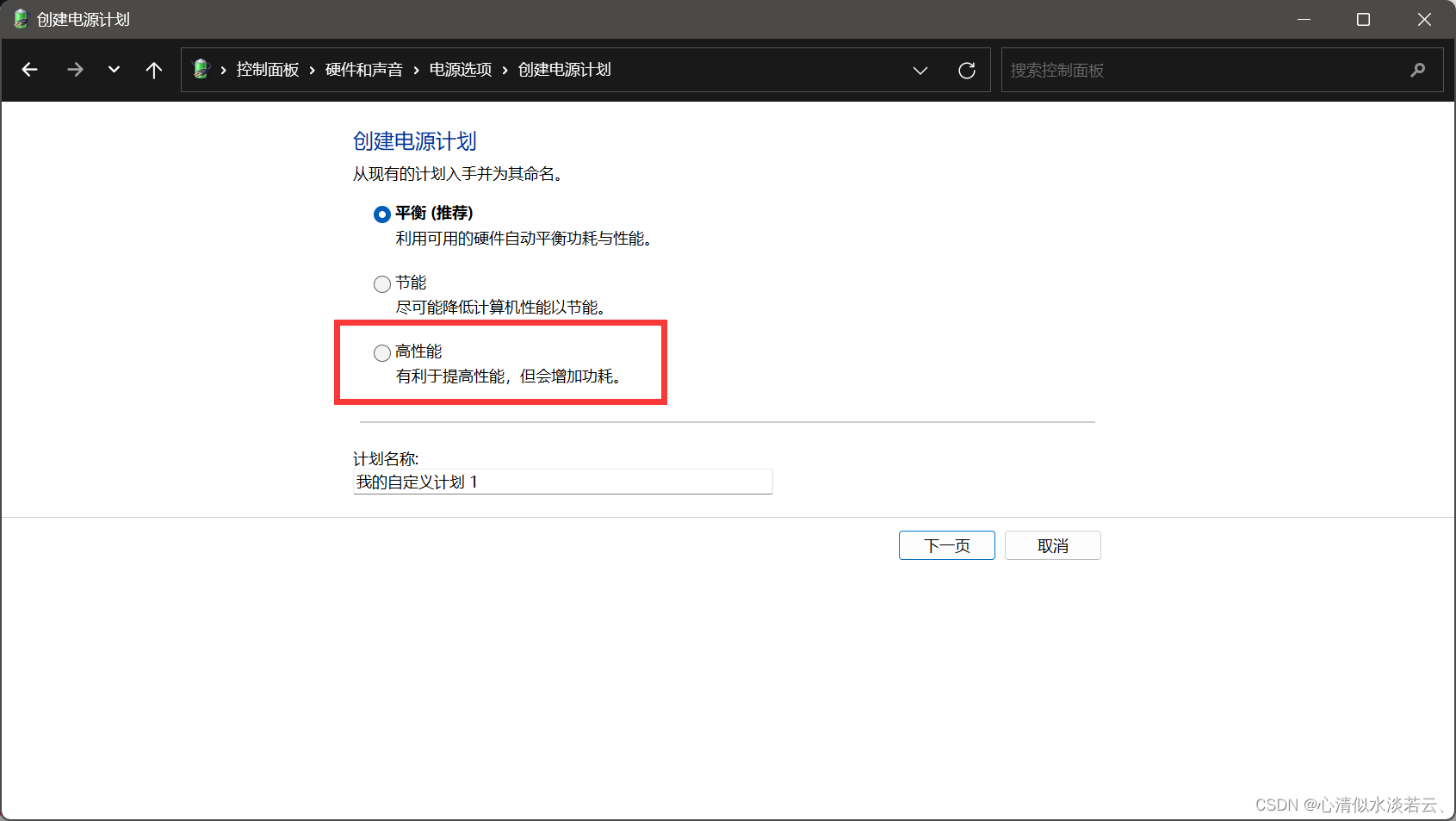
【不限于联想Y9000P电脑关盖再打开时黑屏的解决办法】
不限于联想Y9000P电脑关盖再打开时黑屏的解决办法 问题的前言问题的出现问题拟解决 问题的前言 事情发生在昨天,更新了Win11系统后: 最惹人注目的三处地方就是: 1.可以查看时间的秒数了; 2.右键展示的内容变窄了; 3.按…...
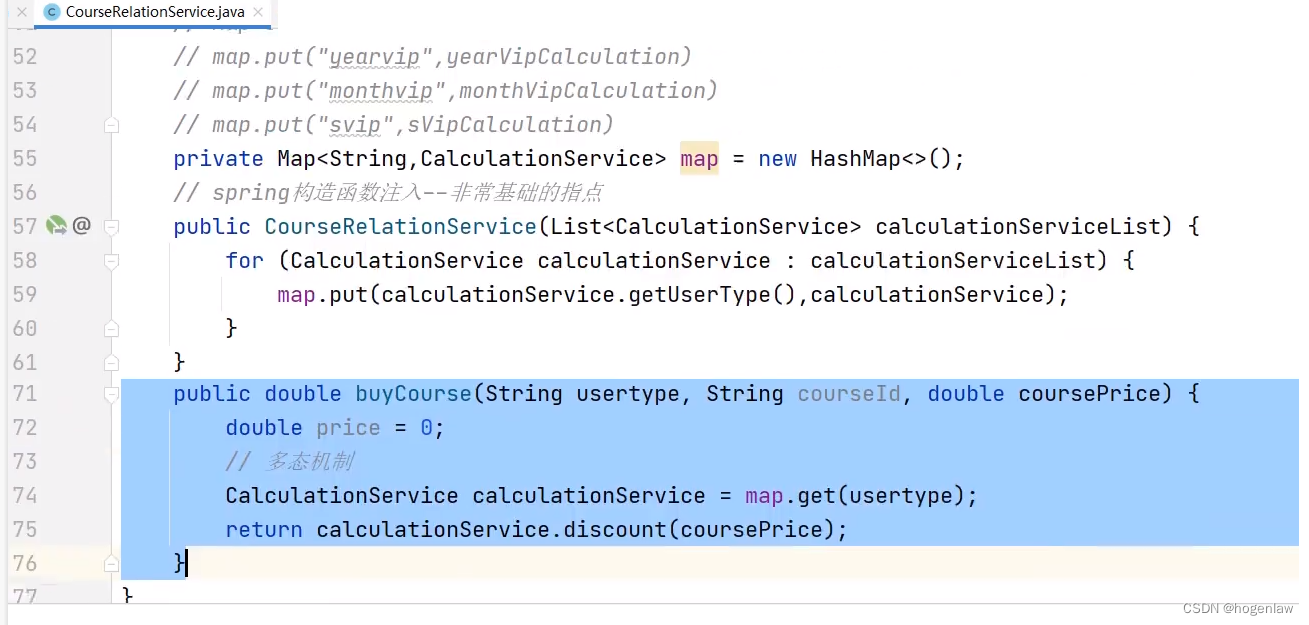
策略模式实战应用
场景 假设做了个卖课网站,会员等级分为月vip、年vip、终生vip,每个等级买课的优惠力度不一样,传统的写法肯定是一堆的 if-else,现在使用策略模式写出代码实现 代码实现 策略模式的核心思想就是对扩展开放,对修改关闭…...

JAVA集合-Map
// 【Map】:双列集合,键值对形式存储,映射关系(kay,value) // 实现:HashMap // 子接口:SortedMap Map的子接口 // 实现类:TreeMap // HashMap // 1。可以插入null // …...

利用Simulink Test进行模型单元测试 - 1
1.搭建用于测试的简单模型 随手搭建了一个demo模型MilTestModel,模型中不带参数 2.创建测试框架 1.模型空白处右击 测试框架 > 为‘MilTestModel’创建 菜单 2.在创建测试框架对话框中,点击OK,对应的测试框架MilTestMode_Harness1就自动…...

深入探讨代理技术:保障网络安全与高效爬虫
1. Socks5代理与IP代理的区别与应用 Socks5代理和IP代理是代理技术中的两个重要方面,它们有着不同的特点和应用场景。Socks5代理是一种协议,支持TCP和UDP流量传输,适用于需要实时数据传输的场景,例如在线游戏或实时通信应用。而I…...
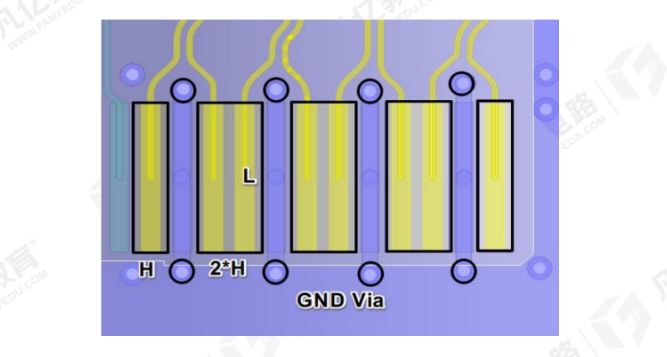
HDMI接口的PCB布局布线要求
高清多媒体接口(High Definition Multimedia Interface),简称:HDMI,是一种全数字化视频和声音发送接口,可以发送未压缩的音频及视频信号。随着技术的不断提升,HDMI的传输速率也不断的提升&#…...
)
Linux tar包安装 Prometheus 和 Grafana(知识点:systemd Unit/重定向)
0. 介绍 用tar包的方式安装 Prometheus 和 Grafana Prometheus:开源的监控方案Grafana:将Prometheus的数据可视化平台 Prometheus已经有了查询功能为什么还需要grafana呢?Prometheus基于promQL这一SQL方言,有一定门槛!Grafana基于浏览器的操作与可视化图表大大降低了理解难…...
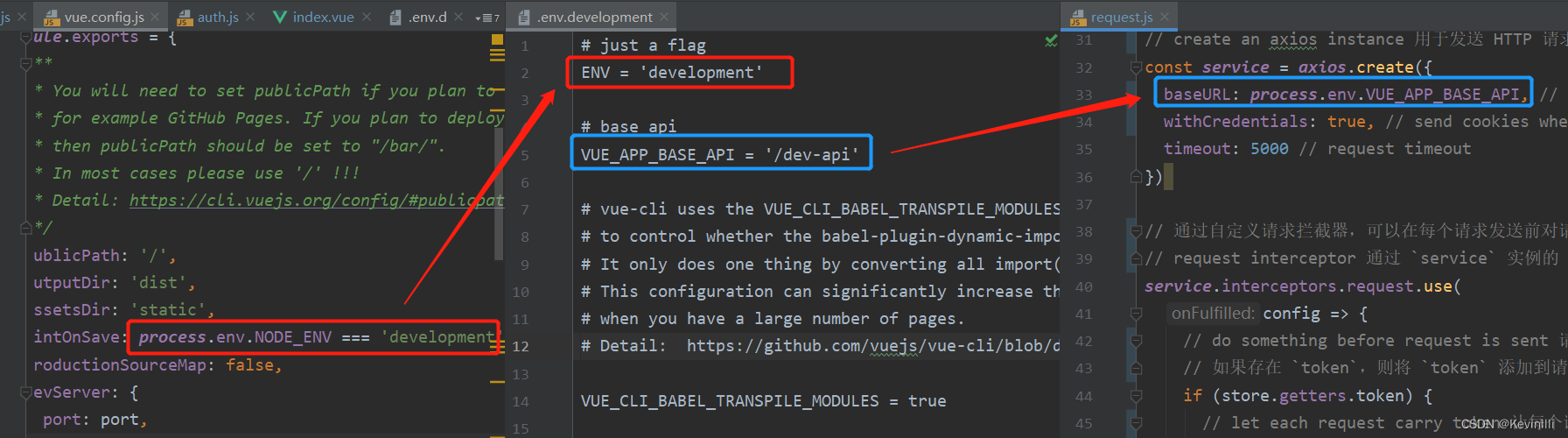
【Vue框架】用户和请求
前言 在上一篇 【Vue框架】Vuex状态管理 针对Vuex状态管理以getters.js进行说明,没有对其中state引入的对象进行详细介绍,因为整体都比较简单,也就不对全部做详细介绍了;但其中的user.js涉及到获取用户的信息、前后端请求的token…...
NGINX组件(rewrite)
一、location匹配的规则和优先级(*) URI:统一资源标识符,是一种字符串标识,用于标识抽象的或者是物理资源;如:文件、图片、视频等 nginx中的URI匹配的是:网址”/“后的路径 如&…...
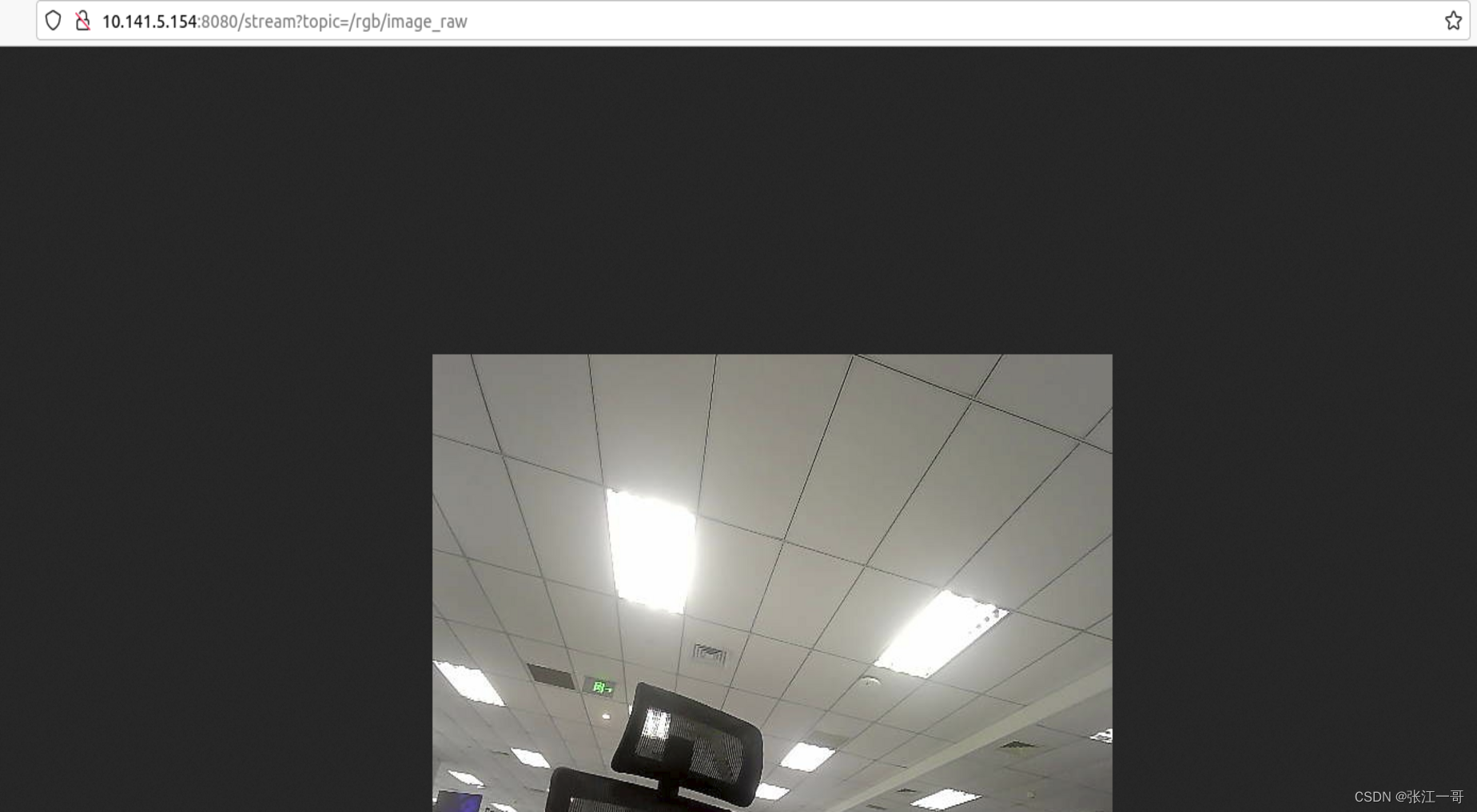
网页显示摄像头数据的方法---基于web video server
1. 背景: 在ros系统中有发布摄像头的相关驱动rgb数据,需求端需要将rgb数据可以直接在网页上去显示。 问题解决: web_video_server功能包,相关链接: web_video_server - ROS Wiki 2. 下载,安装和编译&a…...

SIFT 算法 | 如何在 Python 中使用 SIFT 进行图像匹配
介绍 人类通过记忆和理解来识别物体、人和图像。你看到某件事的次数越多,你就越容易记住它。此外,每当一个图像在你的脑海中弹出时,它就会将该项目或图像与一堆相关的图像或事物联系起来。如果我告诉你我们可以使用一种称为 SIFT 算法的技术来教机器做同样的事情呢? 尽管…...
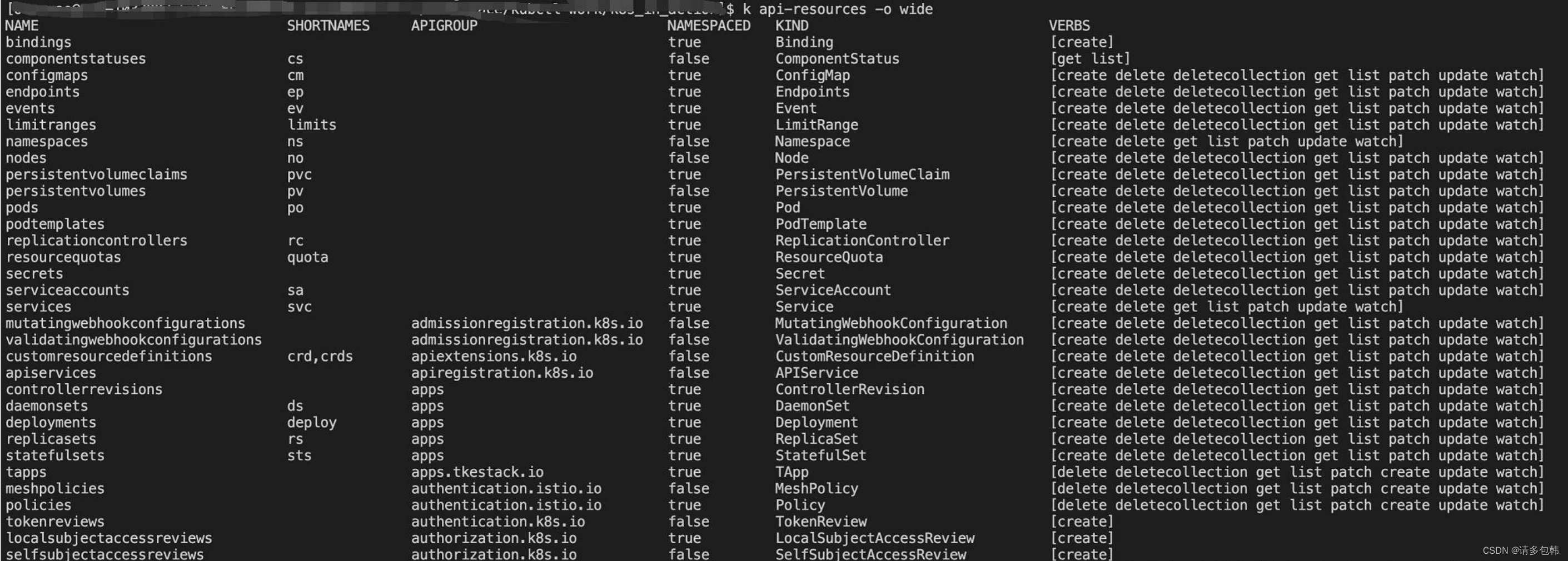
K8S系列四:服务管理
写在前面 本文是K8S系列第四篇,主要面向对k8s新手同学。阅读本文需要读者对k8s的基本概念,比如Pod、Deployment、Service、Namespace等基础概念有所了解,尚且不了解的同学推荐先阅读本系列的第一篇文章《K8S系列一:概念入门》[1]…...

冠达管理:融券卖出交易规则?
融券卖出买卖是指投资者在没有实际持有某只股票的情况下,经过借入该股票并卖出来取得赢利的一种股票买卖方式。融券卖出买卖规矩针对不同市场、不同证券公司之间可能会存在一些差异,但基本的规矩包含如下几个方面。 一、融资融券的资历要求 在进行融券卖…...
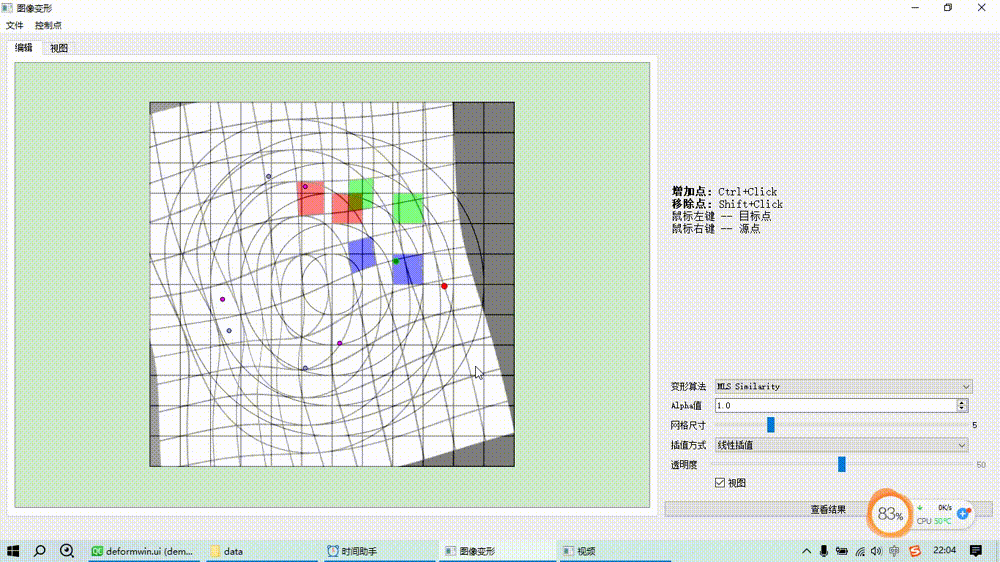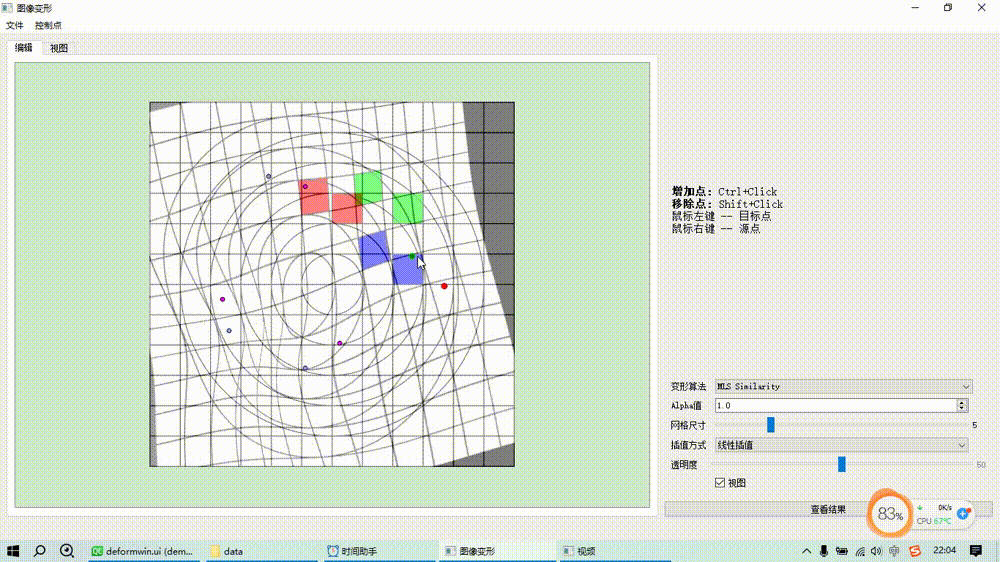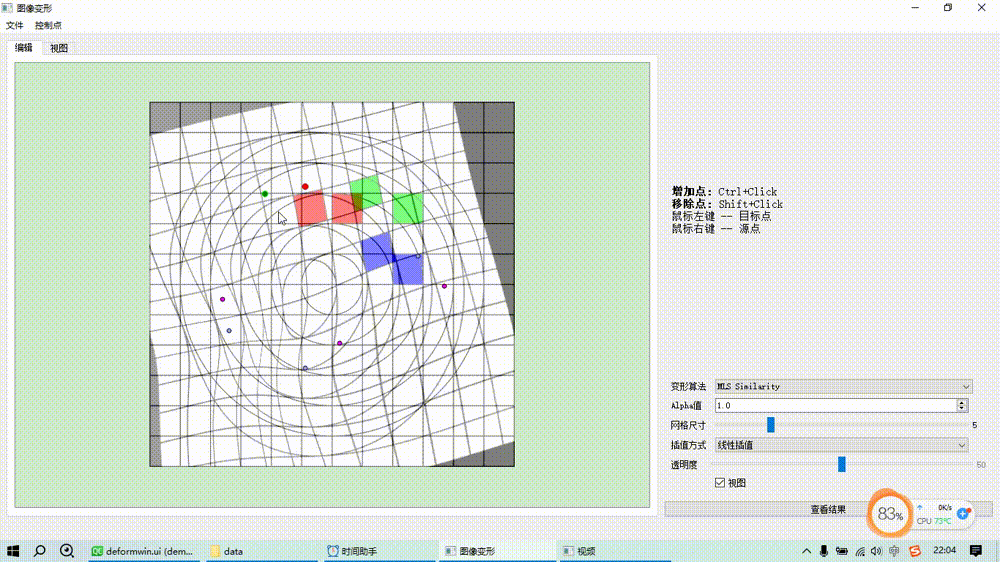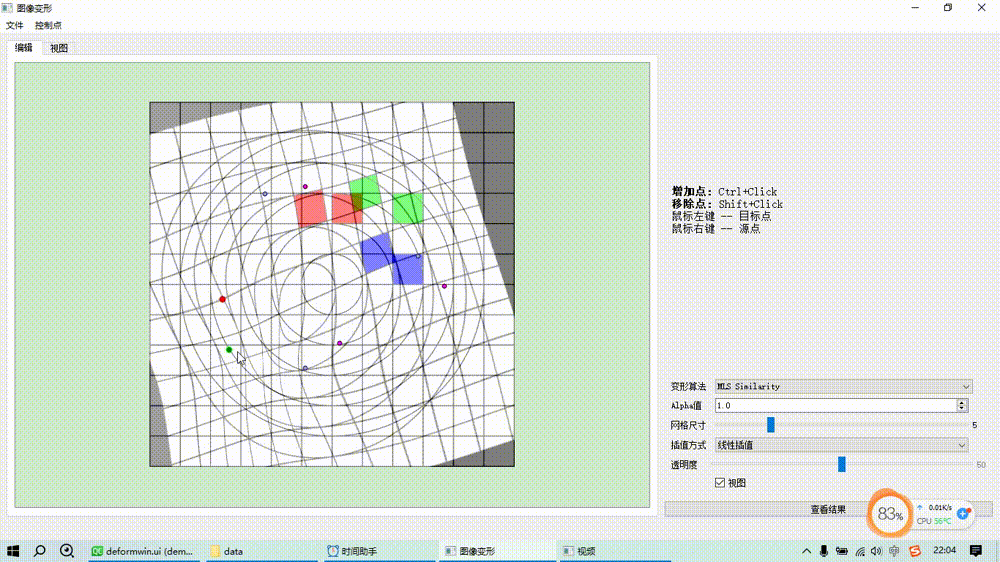
图像变形之移动最小二乘算法(MLS)
基本原理 基于移动最小二乘的图像变形是通过一组源控制点和目标控制点来控制变形,对于每一个待求变形后位置的点而言,根据预设的形变类型(如仿射变换、相似变换、刚性变换)求解一个最小二乘优化目标函数估计一个局部的坐标变换矩阵…...

搭建一个功能齐全的网站
搭建一个功能齐全的网站,需要准备和掌握的一些关键技术和功能可概括如下: 前端技术: HTML/CSS - 网页内容结构和样式JavaScript - 实现网页交互功能前端框架(Vue、React等) - 更高效开发交互页面响应式设计 - 网站适配移动端 后端技术: 服务器(Linux、Nginx等) - 提供网站访…...

Java-jar和war包的区别
jar包和war包的区别: 1、war是一个web模块,其中需要包括WEB-INF,是可以直接运行的WEB模块;jar一般只是包括一些class文件,在声明了Main_class之后是可以用java命令运行的。 2、war包是做好一个web应用后,通…...
分类预测 | MATLAB实现CNN-BiGRU-Attention多输入分类预测
分类预测 | MATLAB实现CNN-BiGRU-Attention多输入单输出分类预测 目录 分类预测 | MATLAB实现CNN-BiGRU-Attention多输入单输出分类预测预测效果基本介绍模型描述程序设计参考资料 预测效果 基本介绍 Matlab实现CNN-BiGRU-Attention多特征分类预测,卷积双向门控循环…...

大数据学习栈记——Neo4j的安装与使用
本文介绍图数据库Neofj的安装与使用,操作系统:Ubuntu24.04,Neofj版本:2025.04.0。 Apt安装 Neofj可以进行官网安装:Neo4j Deployment Center - Graph Database & Analytics 我这里安装是添加软件源的方法 最新版…...

对WWDC 2025 Keynote 内容的预测
借助我们以往对苹果公司发展路径的深入研究经验,以及大语言模型的分析能力,我们系统梳理了多年来苹果 WWDC 主题演讲的规律。在 WWDC 2025 即将揭幕之际,我们让 ChatGPT 对今年的 Keynote 内容进行了一个初步预测,聊作存档。等到明…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个生活电费的缴纳和查询小程序
一、项目初始化与配置 1. 创建项目 ohpm init harmony/utility-payment-app 2. 配置权限 // module.json5 {"requestPermissions": [{"name": "ohos.permission.INTERNET"},{"name": "ohos.permission.GET_NETWORK_INFO"…...

LLM基础1_语言模型如何处理文本
基于GitHub项目:https://github.com/datawhalechina/llms-from-scratch-cn 工具介绍 tiktoken:OpenAI开发的专业"分词器" torch:Facebook开发的强力计算引擎,相当于超级计算器 理解词嵌入:给词语画"…...

HTML前端开发:JavaScript 常用事件详解
作为前端开发的核心,JavaScript 事件是用户与网页交互的基础。以下是常见事件的详细说明和用法示例: 1. onclick - 点击事件 当元素被单击时触发(左键点击) button.onclick function() {alert("按钮被点击了!&…...

多模态大语言模型arxiv论文略读(108)
CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文标题:CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文作者:Sayna Ebrahimi, Sercan O. Arik, Tejas Nama, Tomas Pfister ➡️ 研究机构: Google Cloud AI Re…...

什么?连接服务器也能可视化显示界面?:基于X11 Forwarding + CentOS + MobaXterm实战指南
文章目录 什么是X11?环境准备实战步骤1️⃣ 服务器端配置(CentOS)2️⃣ 客户端配置(MobaXterm)3️⃣ 验证X11 Forwarding4️⃣ 运行自定义GUI程序(Python示例)5️⃣ 成功效果
PAN/FPN
import torch import torch.nn as nn import torch.nn.functional as F import mathclass LowResQueryHighResKVAttention(nn.Module):"""方案 1: 低分辨率特征 (Query) 查询高分辨率特征 (Key, Value).输出分辨率与低分辨率输入相同。"""def __…...

mac:大模型系列测试
0 MAC 前几天经过学生优惠以及国补17K入手了mac studio,然后这两天亲自测试其模型行运用能力如何,是否支持微调、推理速度等能力。下面进入正文。 1 mac 与 unsloth 按照下面的进行安装以及测试,是可以跑通文章里面的代码。训练速度也是很快的。 注意…...

pycharm 设置环境出错
pycharm 设置环境出错 pycharm 新建项目,设置虚拟环境,出错 pycharm 出错 Cannot open Local Failed to start [powershell.exe, -NoExit, -ExecutionPolicy, Bypass, -File, C:\Program Files\JetBrains\PyCharm 2024.1.3\plugins\terminal\shell-int…...
