神经网络基础-神经网络补充概念-11-向量化逻辑回归
概念
通过使用 NumPy 数组来进行矩阵运算,将循环操作向量化。
向量化的好处在于它可以同时处理多个样本,从而加速计算过程。在实际应用中,尤其是处理大规模数据集时,向量化可以显著提高代码的效率。
代码实现-以逻辑回归为例
import numpy as npdef sigmoid(z):return 1 / (1 + np.exp(-z))def compute_loss(X, y, theta):m = len(y)h = sigmoid(X.dot(theta))loss = (-1/m) * np.sum(y * np.log(h) + (1 - y) * np.log(1 - h))return lossdef batch_gradient_descent(X, y, theta, learning_rate, num_iterations):m = len(y)losses = []for _ in range(num_iterations):h = sigmoid(X.dot(theta))gradient = X.T.dot(h - y) / mtheta -= learning_rate * gradientloss = compute_loss(X, y, theta)losses.append(loss)return theta, losses# 生成一些模拟数据
np.random.seed(42)
m = 100
n = 2
X = np.random.randn(m, n)
X = np.hstack((np.ones((m, 1)), X))
theta_true = np.array([1, 2, 3])
y = (X.dot(theta_true) + np.random.randn(m) * 0.2) > 0# 初始化参数和超参数
theta = np.zeros(X.shape[1])
learning_rate = 0.01
num_iterations = 1000# 执行批量梯度下降(向量化)
theta_optimized, losses = batch_gradient_descent(X, y, theta, learning_rate, num_iterations)# 打印优化后的参数
print("优化后的参数:", theta_optimized)# 绘制损失函数下降曲线
import matplotlib.pyplot as plt
plt.plot(losses)
plt.xlabel('迭代次数')
plt.ylabel('损失')
plt.title('损失函数下降曲线')
plt.show()相关文章:

神经网络基础-神经网络补充概念-11-向量化逻辑回归
概念 通过使用 NumPy 数组来进行矩阵运算,将循环操作向量化。 向量化的好处在于它可以同时处理多个样本,从而加速计算过程。在实际应用中,尤其是处理大规模数据集时,向量化可以显著提高代码的效率。 代码实现-以逻辑回归为例 i…...

openGauss学习笔记-40 openGauss 高级数据管理-锁
文章目录 openGauss学习笔记-40 openGauss 高级数据管理-锁40.1 语法格式40.2 参数说明40.3 示例 openGauss学习笔记-40 openGauss 高级数据管理-锁 如果需要保持数据库数据的一致性,可以使用LOCK TABLE来阻止其他用户修改表。 例如,一个应用需要保证表…...
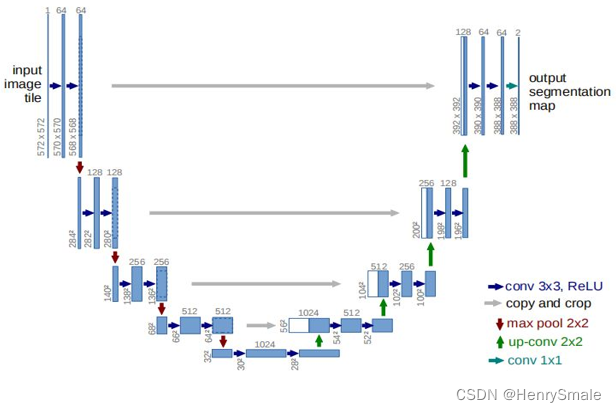
勘探开发人工智能技术:机器学习(6)
0 提纲 7.1 循环神经网络RNN 7.2 LSTM 7.3 Transformer 7.4 U-Net 1 循环神经网络RNN 把上一时刻的输出作为下一时刻的输入之一. 1.1 全连接神经网络的缺点 现在的任务是要利用如下语料来给apple打标签: 第一句话:I like eating apple!(我喜欢吃苹…...

代理类型中的 HTTP、HTTPS 和 SOCKS 有什么区别?
HTTP、HTTPS 和 SOCKS 都是代理(Proxy)协议,用于在网络通信中转发请求和响应,但它们在工作原理和用途上有一些区别。下面是它们之间的主要区别: HTTP代理: 工作原理: HTTP 代理主要用于转发 HTT…...
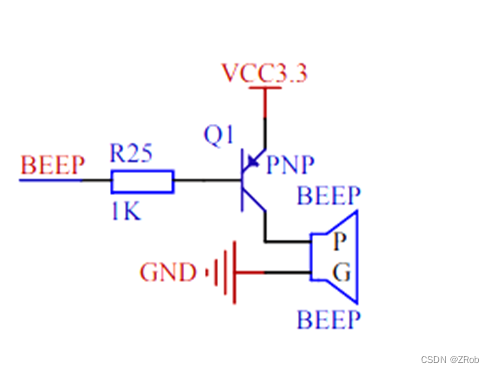
【STM32RT-Thread零基础入门】 3. PIN设备(GPIO)的使用
硬件:STM32F103ZET6、ST-LINK、usb转串口工具、4个LED灯、1个蜂鸣器、4个1k电阻、2个按键、面包板、杜邦线 文章目录 前言一、PIN设备介绍1. 引脚编号获取2. 设置引脚的输入/输出模式3. 设置引脚的电平值4. 读取引脚的电平值5. 绑定引脚中断回调函数6. 脱离引脚中断…...
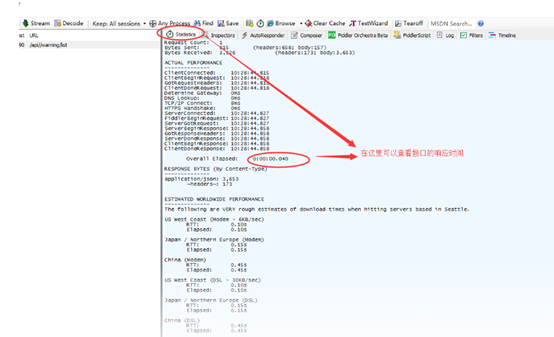
fiddler抓包工具的用法以及抓取手机报文定位bug
前言: fiddler抓包工具是日常测试中常用的一种bug定位工具 一 抓取https报文步骤 使用方法: 1 首先打开fiddler工具将证书导出 点击TOOLS------Options------Https-----Actions---选中第二个选项 2 把证书导出到桌面后 打开谷歌浏览器 设置---高级…...

spring中时间格式化的两种方式
方法一:自己格式化 自己写一个格式化的类,把date类型的时间传进去: public class DateUtil {public static String formatDate(Date date){SimpleDateFormat simpleDateFormatnew SimpleDateFormat("yyyy-MM-dd HH:mm:ss");retur…...
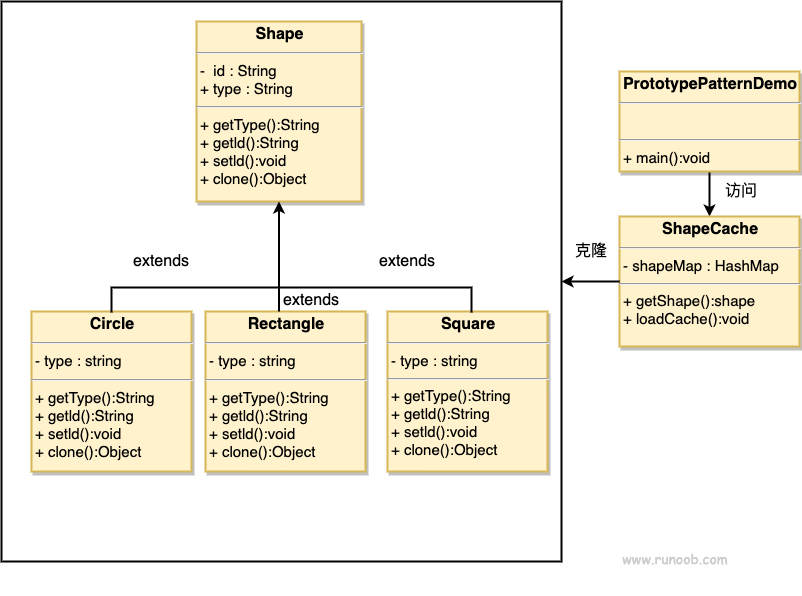
【设计模式】原型模式
原型模式(Prototype Pattern)是用于创建重复的对象,同时又能保证性能。这种类型的设计模式属于创建型模式,它提供了一种创建对象的最佳方式之一。 这种模式是实现了一个原型接口,该接口用于创建当前对象的克隆。当直接…...
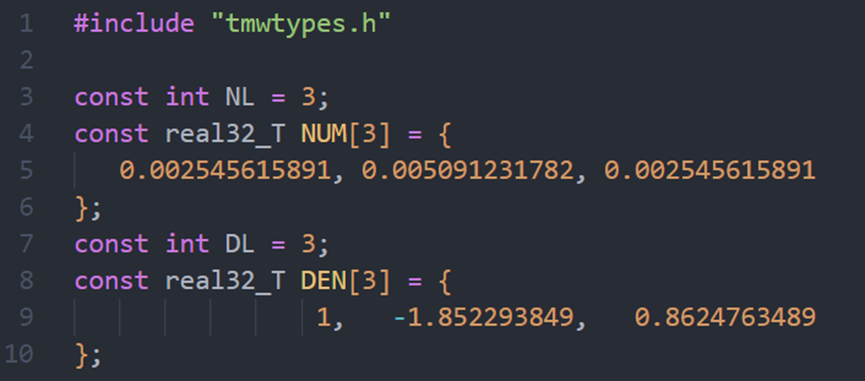
Matlab的Filter Designer工具设计二阶低通滤波器
Matlab版本:2018b 本文要求:设计一个二阶巴特沃斯低通滤波器用于嵌入式软件滤波,传感器采样频率是20KHz,截止频率是333Hz,获取滤波系数,本文不包括二阶滤波推导和代码编写。 打开Matlab->APP->Filt…...

软件测试基础篇——LAMP环境搭建
LAMP 1、Linux系统的其他命令 find命令:在目录下查找文件 格式一:find 路径 参数 文件名 路径:如果没有指定路径,默认是在当前目录下 参数:-name 根据文件名来查找,区分大小写; -…...

使用dom4j将xml转为String并去掉所有格式
文章目录 功能描述实现代码 功能描述 有以下xml内容,需要转成String字符串。同时,要去掉文中所有格式。 <root><student><name>张三</name><sex>男</sex><age>16</age><class>1班</class>…...
wsl2安装docker引擎(Install Docker Engine on Debian)
安装 1.卸载旧版本 在安装 Docker 引擎之前,您必须首先确保卸载任何冲突的软件包。 发行版维护者在他们的存储库。必须先卸载这些软件包,然后才能安装 Docker 引擎的正式版本。 要卸载的非官方软件包是: docker.iodocker-composedocker-…...

百日筑基篇——python爬虫学习(一)
百日筑基篇——python爬虫学习(一) 文章目录 前言一、python爬虫介绍二、URL管理器三、所需基础模块的介绍1. requests2. BeautifulSoup1. HTML介绍2. 网页解析器 四、实操1. 代码展示2. 代码解释1. 将大文件划分为小的文件(根据AA的ID数量划…...
【Spring专题】Spring之底层架构核心概念解析
目录 前言前置知识课程内容一、BeanDefinition:图纸二、BeanDefinitionReader:图纸注册器——Spring工厂基础设施之一2.1 AnnotatedBeanDefinitionReader2.2 XmlBeanDefinitionReader2.3 ClassPathBeanDefinitionScanner基本介绍总结使用示例 三、BeanFa…...

electron 使用node C++插件 node-gyp
node C插件使用,在我们常规使用中,需要使用node-gyp指定对饮的node版本即可 在electron的使用中,我们需要指定的是electron版本要不然会报错使用的v8内核版本不一致导致C扩展无法正常引入 electron官方文档-node原生模块 package.json {&quo…...
)
学习Vue:使用条件渲染指令(v-if,v-else,v-show)
在 Vue.js 中,条件与循环是实现动态交互界面的关键要素。通过使用条件渲染指令,您可以根据不同的条件决定是否显示或隐藏特定的内容。在本文中,我们将介绍三个常用的条件渲染指令:v-if、v-else 和 v-show,以及它们的用…...

【图像去噪的滤波器】非局部均值滤波器的实现,用于鲁棒的图像去噪研究(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...

Redis辅助功能
一、Redis队列 1.1、订阅 subscribe ch1 ch2 1.2 publish:发布消息 publish channel message 1.3 unsubscribe: 退订 channel 1.4 模式匹配 psubscribe ch* 模糊发布,订阅,退订, p* <channelName> 1.5 发布订阅原理 订阅某个频道或…...
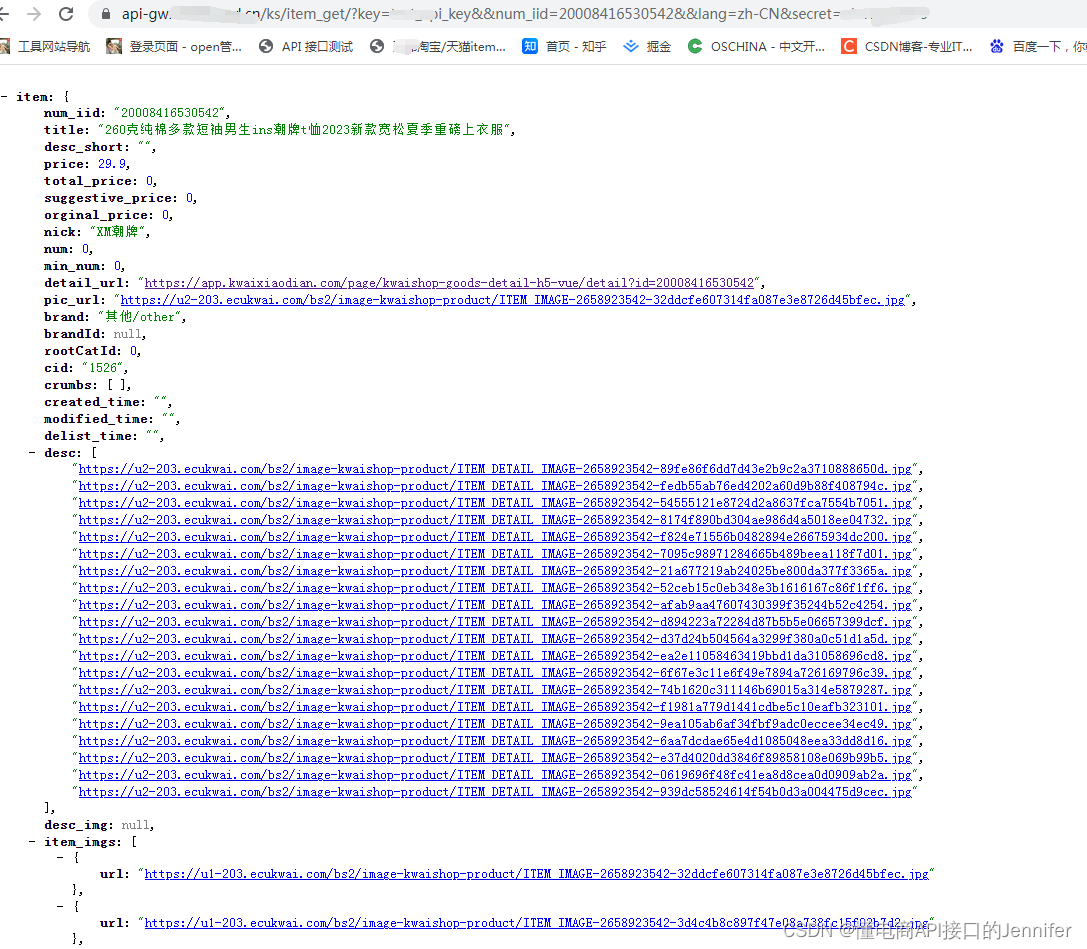
快手商品详情数据API 抓取快手商品价格、销量、库存、sku信息
快手商品详情数据API是用来获取快手商品详情页数据的接口,请求参数为商品ID,这是每个商品唯一性的标识。返回参数有商品标题、商品标题、商品简介、价格、掌柜昵称、库存、宝贝链接、宝贝图片、商品SKU等。 接口名称:item_get 公共参数 名…...

linux系统部署jenkins详细教程
一、Linux环境 1、下载war包 官网下载地址: https://get.jenkins.io/war-stable/2.332.4/jenkins.war 2、将war包上传至服务器 创建目录/home/ubuntu/jenkins 上传war包至该目录 3、将jenkins添加到环境变量 进入环境变量文件 vim /etc/profile # 文件下方追加…...

FastAPI 教程:从入门到实践
FastAPI 是一个现代、快速(高性能)的 Web 框架,用于构建 API,支持 Python 3.6。它基于标准 Python 类型提示,易于学习且功能强大。以下是一个完整的 FastAPI 入门教程,涵盖从环境搭建到创建并运行一个简单的…...

DIY|Mac 搭建 ESP-IDF 开发环境及编译小智 AI
前一阵子在百度 AI 开发者大会上,看到基于小智 AI DIY 玩具的演示,感觉有点意思,想着自己也来试试。 如果只是想烧录现成的固件,乐鑫官方除了提供了 Windows 版本的 Flash 下载工具 之外,还提供了基于网页版的 ESP LA…...

学习STC51单片机31(芯片为STC89C52RCRC)OLED显示屏1
每日一言 生活的美好,总是藏在那些你咬牙坚持的日子里。 硬件:OLED 以后要用到OLED的时候找到这个文件 OLED的设备地址 SSD1306"SSD" 是品牌缩写,"1306" 是产品编号。 驱动 OLED 屏幕的 IIC 总线数据传输格式 示意图 …...

2025 后端自学UNIAPP【项目实战:旅游项目】6、我的收藏页面
代码框架视图 1、先添加一个获取收藏景点的列表请求 【在文件my_api.js文件中添加】 // 引入公共的请求封装 import http from ./my_http.js// 登录接口(适配服务端返回 Token) export const login async (code, avatar) > {const res await http…...

微信小程序云开发平台MySQL的连接方式
注:微信小程序云开发平台指的是腾讯云开发 先给结论:微信小程序云开发平台的MySQL,无法通过获取数据库连接信息的方式进行连接,连接只能通过云开发的SDK连接,具体要参考官方文档: 为什么? 因为…...

什么?连接服务器也能可视化显示界面?:基于X11 Forwarding + CentOS + MobaXterm实战指南
文章目录 什么是X11?环境准备实战步骤1️⃣ 服务器端配置(CentOS)2️⃣ 客户端配置(MobaXterm)3️⃣ 验证X11 Forwarding4️⃣ 运行自定义GUI程序(Python示例)5️⃣ 成功效果
第 86 场周赛:矩阵中的幻方、钥匙和房间、将数组拆分成斐波那契序列、猜猜这个单词
Q1、[中等] 矩阵中的幻方 1、题目描述 3 x 3 的幻方是一个填充有 从 1 到 9 的不同数字的 3 x 3 矩阵,其中每行,每列以及两条对角线上的各数之和都相等。 给定一个由整数组成的row x col 的 grid,其中有多少个 3 3 的 “幻方” 子矩阵&am…...
-HIve数据分析)
大数据学习(132)-HIve数据分析
🍋🍋大数据学习🍋🍋 🔥系列专栏: 👑哲学语录: 用力所能及,改变世界。 💖如果觉得博主的文章还不错的话,请点赞👍收藏⭐️留言Ǵ…...

关键领域软件测试的突围之路:如何破解安全与效率的平衡难题
在数字化浪潮席卷全球的今天,软件系统已成为国家关键领域的核心战斗力。不同于普通商业软件,这些承载着国家安全使命的软件系统面临着前所未有的质量挑战——如何在确保绝对安全的前提下,实现高效测试与快速迭代?这一命题正考验着…...

QT3D学习笔记——圆台、圆锥
类名作用Qt3DWindow3D渲染窗口容器QEntity场景中的实体(对象或容器)QCamera控制观察视角QPointLight点光源QConeMesh圆锥几何网格QTransform控制实体的位置/旋转/缩放QPhongMaterialPhong光照材质(定义颜色、反光等)QFirstPersonC…...
