arcgis数据采集与拓扑检查
1、已准备好一张配准好的浙江省行政区划图,如下:
2、现在需要绘制湖州市县级行政区划。需要右击文件夹新建文件地理数据库,如下:

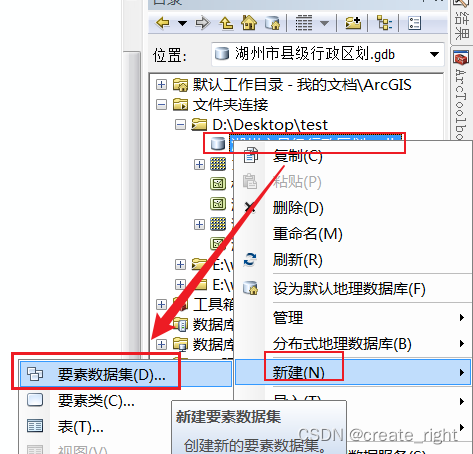
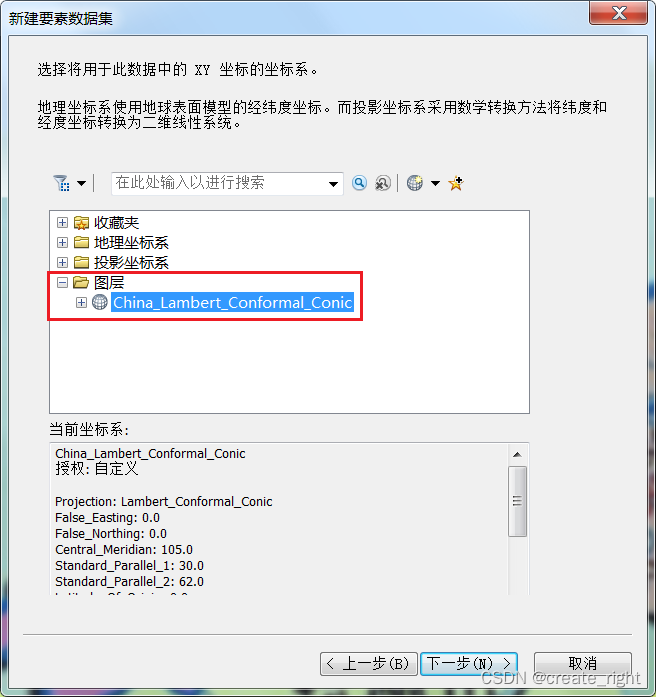
其余步骤均默认即可。
创建好县级要素数据集后,再新建要素类,命名为县。
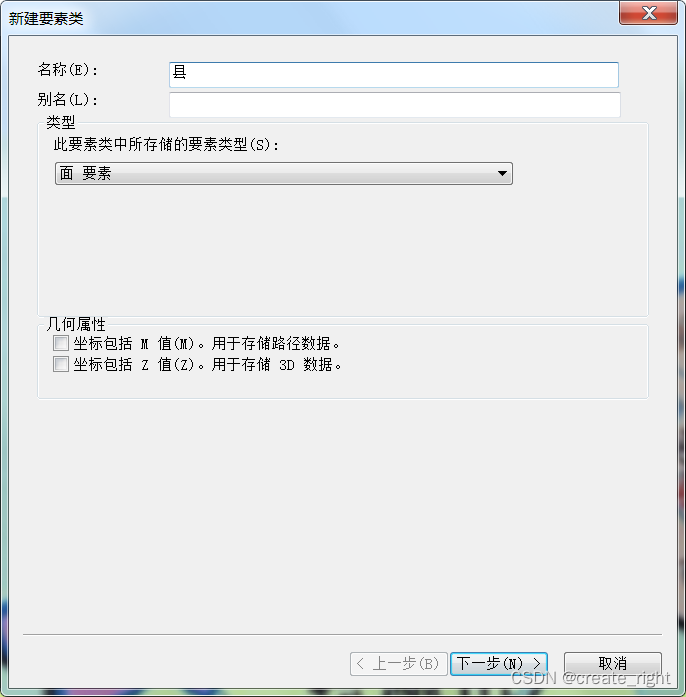

为要素类添加三个字段,具体见上图。其余均默认设置。创建成功后,将要素类导入arcmap中。
3、打开编辑器,选择开始编辑,随后点击创建要素按钮,开始沿着配准好的地图采集数据。如下:


开始采集湖州市县级行政区划边界,如下:

4、采集后填写属性信息。需要单击属性按钮,然后在右侧填写属性信息,比如所属省份等。
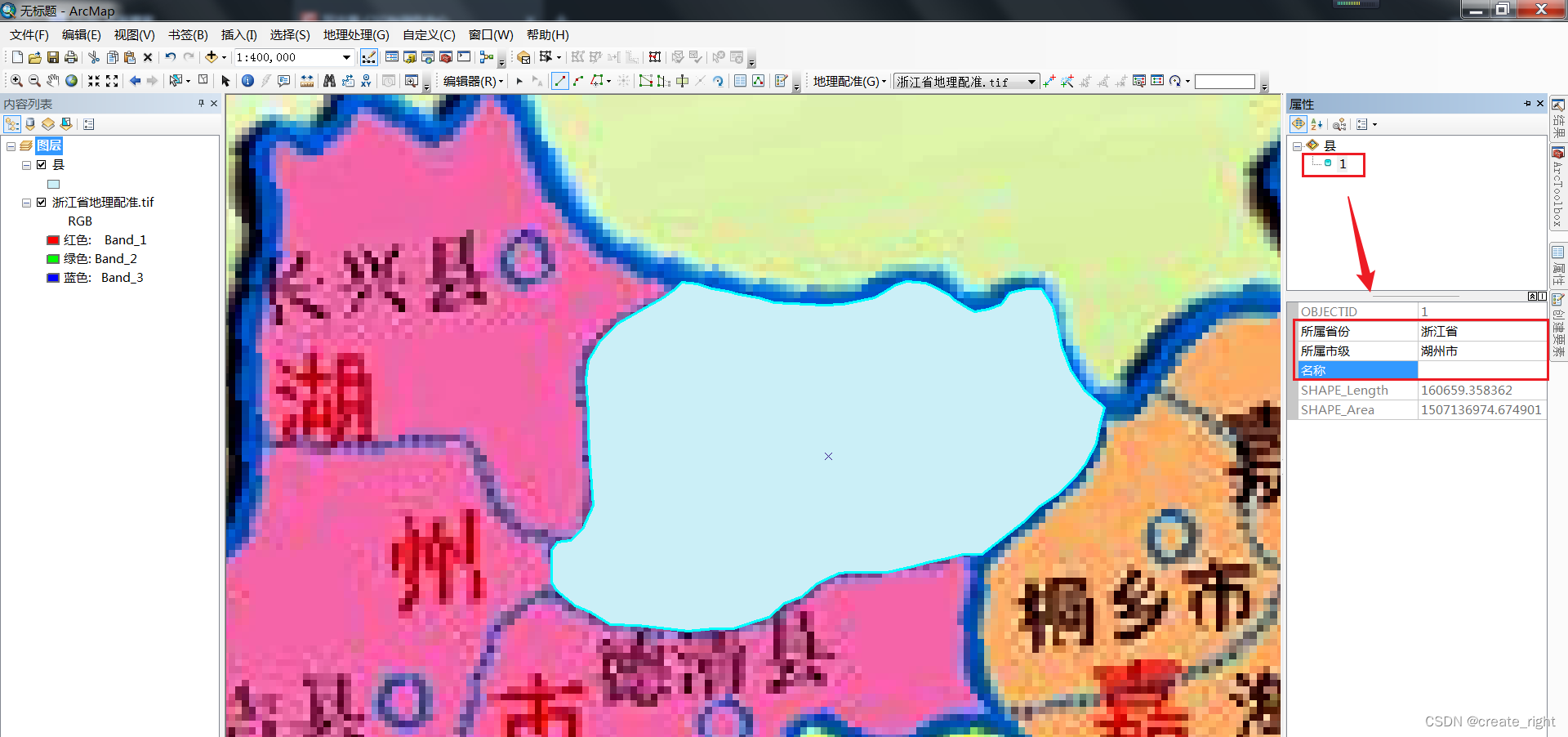
调整县层的透明度,再绘制其他县级行政区划。

先不需要管绘制的边界是否重叠或空缺,后面的拓扑检查会解决这个问题,继续绘制其他县的边界。绘制完成后,点击保存编辑,并退出编辑。

5、右键要素数据集,选择新建,新建拓扑。具体如下:
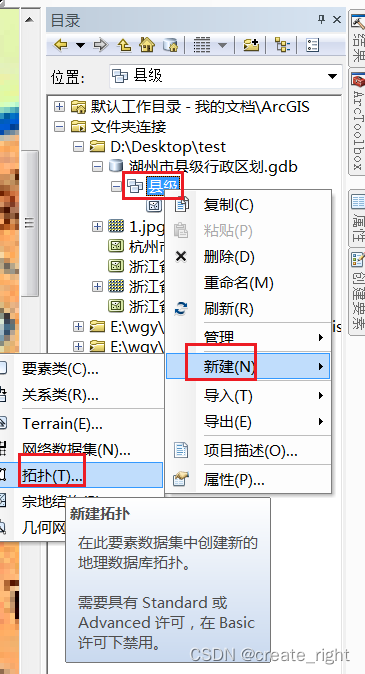

添加两个规则,如上图所示。其余页面选择默认即可,一直点击下一步,直到完成。

将拓扑拖入arcmap中,点击开始编辑按钮,开始对错误进行修改。

6、对于不能有空隙的错误,选择创建新要素,然后按住shift键选择两个要素,将其合并即可。调出拓扑工具,选择错误检查器,查看错误列表。
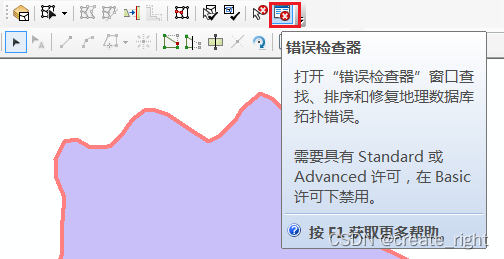

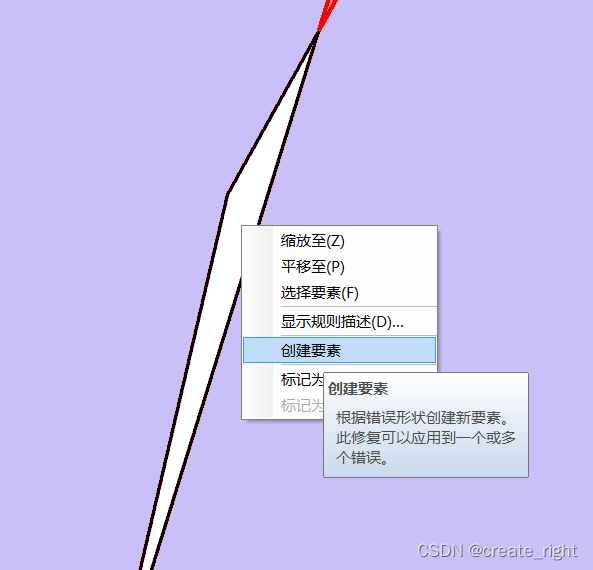
对于不能有空隙类的错误,需要先创建要素填充,然后选择与邻接要素合并。
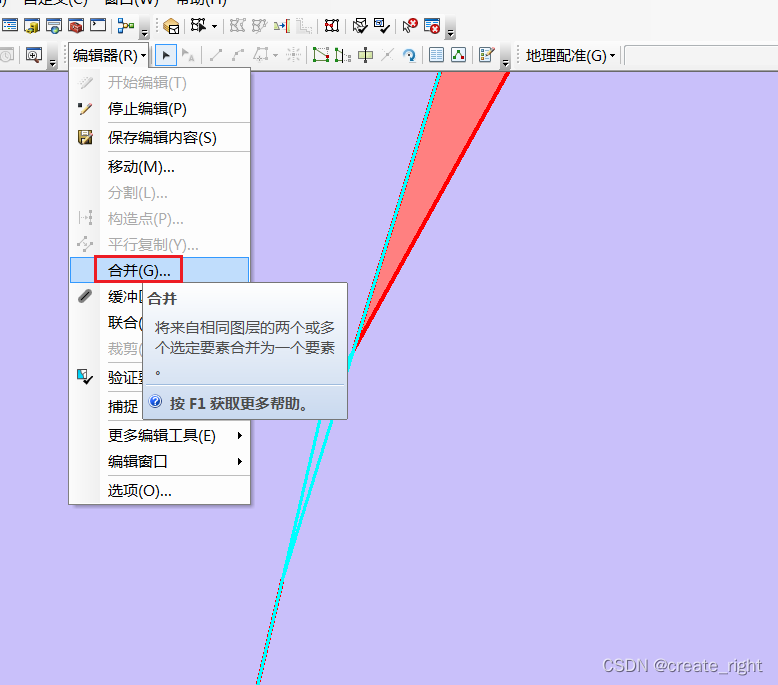

7、对于不能重叠类的错误,选择合并即可。
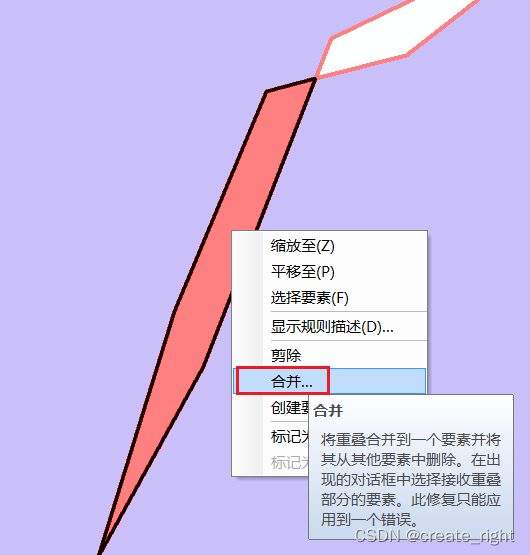
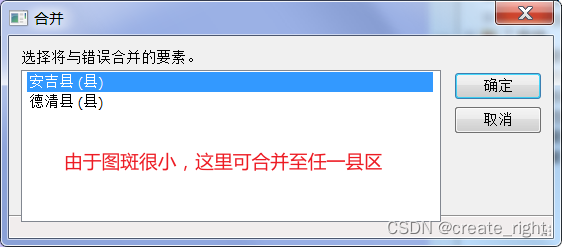
8、两类错误全部处理好之后,就能得到湖州市的县级行政区划数据了。如下:
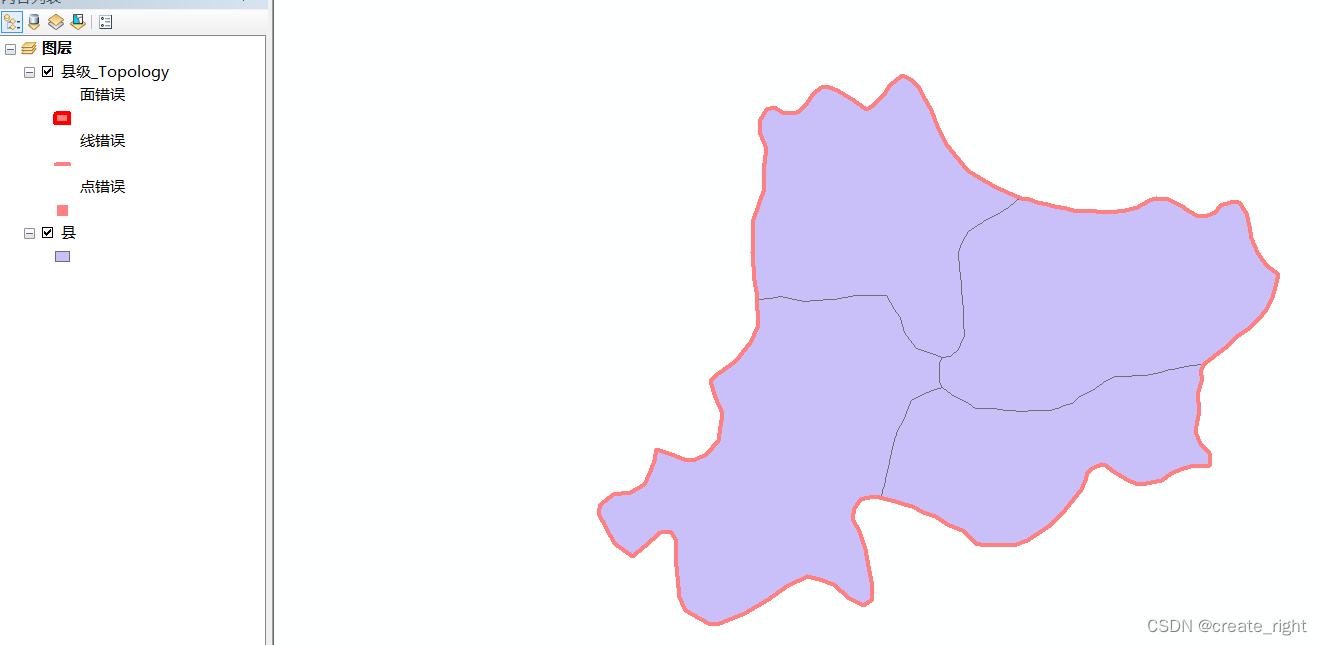
由于外围是空白的,所以拓扑检查时将其判断为不能有空隙类错误,实际上这个错误是可以直接忽略的,因为我们所需要的就是湖州市的县级行政区划,外围必然为空,故此错误无法避免,故将其忽略。
相关文章:

arcgis数据采集与拓扑检查
1、已准备好一张配准好的浙江省行政区划图,如下: 2、现在需要绘制湖州市县级行政区划。需要右击文件夹新建文件地理数据库,如下: 其余步骤均默认即可。 创建好县级要素数据集后,再新建要素类,命名为县。 为…...
【前端 | CSS】滚动到底部加载,滚动监听、懒加载
背景 在日常开发过程中,我们会遇到图片懒加载的功能,基本原理是,滚动条滚动到底部后再次获取数据进行渲染。 那怎么判断滚动条是否滚动到底部呢?滚动条滚动到底部触发时间的时机和方法又该怎样定义? 针对以上问题我…...

word将mathtype公式批量转为latex公式
最近,由于工作学习需要,要将word里面的mathype公式转为latex公式。 查了查资料,有alt\的操作,这样太慢了。通过下面链接的操作,结合起来可以解决问题。 某乎:https://www.zhihu.com/question/532353646 csd…...
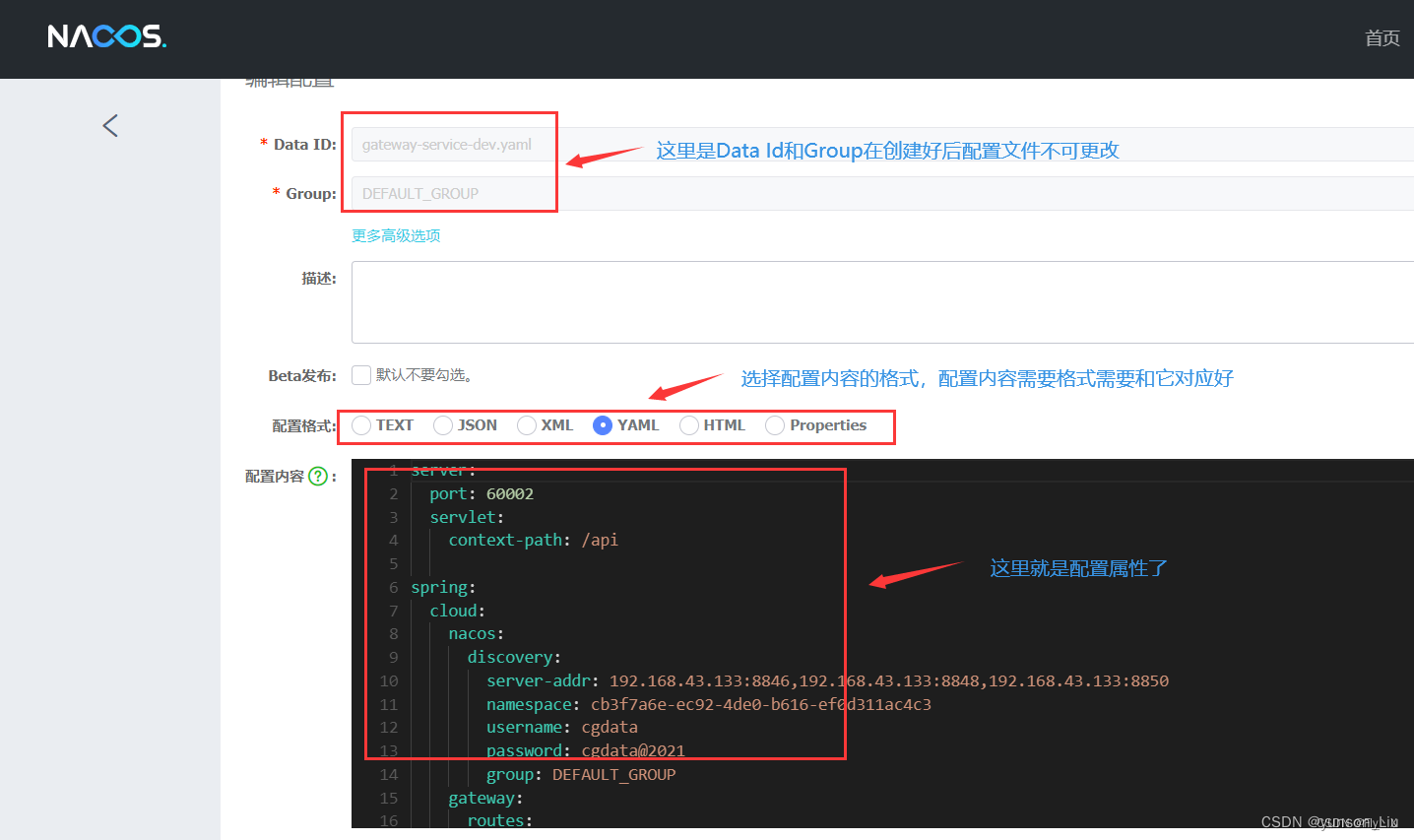
docker-compose部署nacos 2.2.3
1、编写docker-compose.yml文件 version: "3.1" services:nacos:restart: alwaysimage: nacos/nacos-server:v2.2.3container_name: nacosenvironment:- NACOS_AUTH_ENABLEtrue- MODEstandalone- NACOS_AUTH_TOKEN8b92c609089f74db3c5ee04bd7d4d89e8b92c609089f74db…...
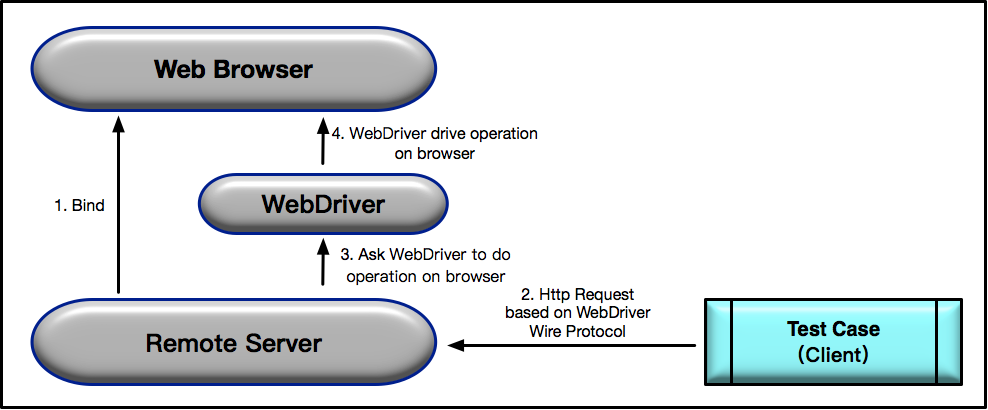
软件测试52讲-学习笔记
测试基础知识篇(11讲) 01 你真的懂测试吗?从“用户登录”测试谈起 测试用例设计框架 基于功能性需求和非功能性需求思考: 功能性需求使用等价类划分、边界值分析、错误推断法设计用例 非功能性需求考虑安全(信息的保存…...

【ARM 嵌入式 编译系列 4 -- GCC 编译属性 __read_mostly 详细介绍】
文章目录 __read_mostly 介绍__read_mostly 在 linux 中的使用.data.read_mostly 介绍 __read_mostly 介绍 __read_mostly 是一个在Linux内核编程中用到的宏定义,这是一个gcc编译器的属性,用于告诉编译器此变量主要用于读取,很少进行写入&am…...
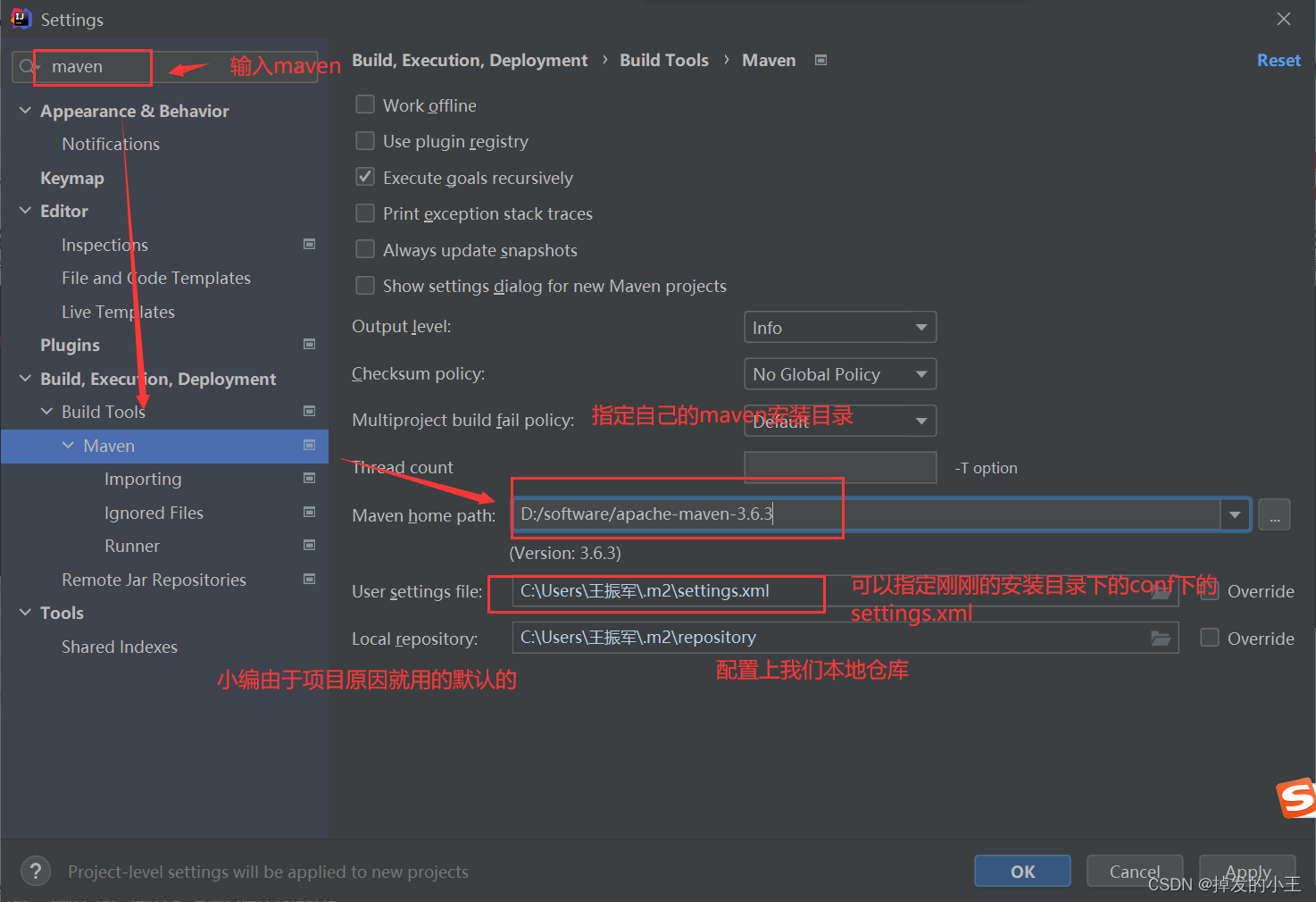
Maven在IDEA2021版本中全局配置(一次配置处处生效)
前言 我们在开发中,Maven是必不可少的,但是每次都需要设置一遍Maven的仓库和settings.xml。真的是心累,今天教大家全局配置一下。再也不要每次项目都配了,Maven还经常出问题。 解决方案 友情提示:小编的IDEA版本为2…...

名侦探番外——Arduino“炸弹”引爆摩天大楼
名侦探番外——Arduino“炸弹”引爆摩天大楼 硬件准备1.材料准备2.模块介绍 电路设计1.硬件接线 程序设计1.设计思路2.部分程序3.功能优化 总结 好久不见,童鞋们!小编突然想到很久以前看的柯南剧场版——计时引爆摩天大楼的情景,对剧里的“炸…...
自适应AI chatgpt智能聊天创作官网html源码
我们致力于开发先进的自适应AI智能聊天技术,旨在为用户提供前所未有的聊天体验。通过融合自然语言处理、机器学习和深度学习等领域的顶尖技术,我们的智能聊天系统能够准确理解用户的需求并给出相应的回应。 我们的自适应AI智能聊天系统具备以下核心特点…...

防抖,节流
概念 防抖(debounce):类似法师技能读条,读条没完再按技能就会重新读条,在触发后的n秒内只会执行一次,若在这n秒内重复触发则重新计算 节流(throttle):连续发生的事件在n秒内只执行一次函数 参考 【前端面试必问】—…...
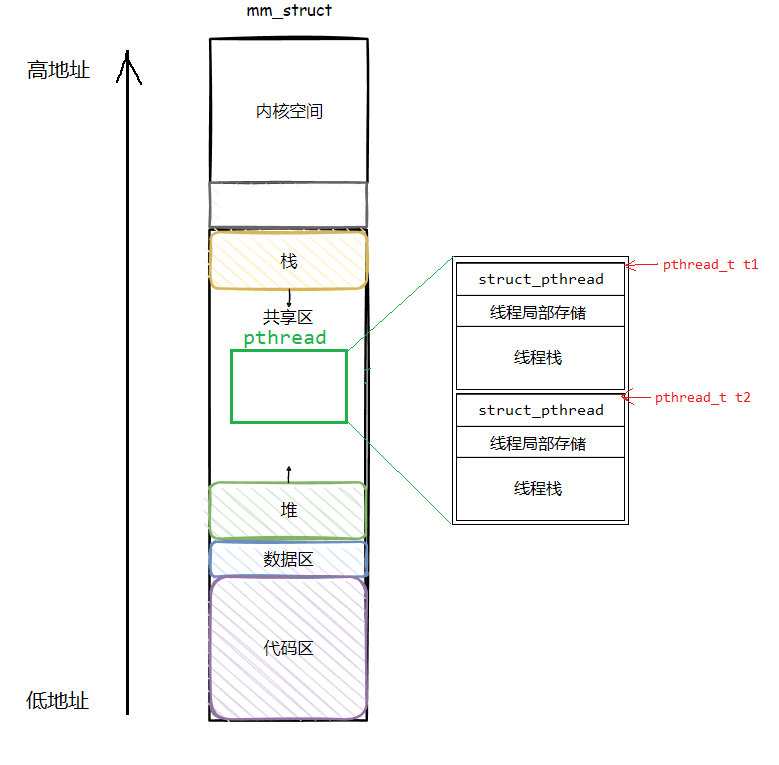
【Linux】多线程1——线程概念与线程控制
文章目录 1. 线程概念什么是线程Linux中的线程线程的优点线程的缺点线程的独立资源和共享资源 2. 线程控制Linux的pthread库用户级线程 📝 个人主页 :超人不会飞)📑 本文收录专栏:《Linux》💭 如果本文对您有帮助&…...
【Maven】SpringBoot项目使用maven-assembly-plugin插件多环境打包
SpringBoot项目使用maven-assembly-plugin插件多环境打包 1.创建SpringBoot项目并在pom.xml文件中添加maven-assembly-plugin配置 <!-- 多环境配置 --><profiles><!-- 开发环境 --><profile><id>dev</id><properties><prof…...

指令集_基础
指令集-基础 一、提示过程1,文章摘要2,数学问题求解 二、角色提示三、多范例提示 一、提示过程 指导人工智能,执行任务的过程,称为提示过程。向AI 提供一组指令(提示),然后它执行任务 1,文章摘要 例如&a…...

学习Vue:数据绑定的基本概念
在 Vue.js 中,Vue 实例是您构建应用程序的核心。它允许您将数据和界面连接起来,实现动态的数据绑定,使您的应用程序能够根据数据的变化自动更新界面。让我们来深入了解 Vue 实例与数据绑定的基本概念。 Vue 实例与数据绑定 什么是 Vue 实例&…...
 - 迭代器 - 生成器 - 闭包)
Python 装饰器 - 推导式(列表推导式) - 迭代器 - 生成器 - 闭包
目录 推导式 1、列表推导式(用得最多的) 给你一个列表,求所有数据的绝对值 列表推导式跟if运算 打印50以内能被3整除的数的平方(filter)(if的使用) 找到1000以内开平方的结果是整数的数&am…...

【大数据】Flink 详解(二):核心篇 Ⅲ
Flink 详解(二):核心篇 Ⅲ 29、Flink 通过什么实现可靠的容错机制? Flink 使用 轻量级分布式快照,设计检查点(checkpoint)实现可靠容错。 30、什么是 Checkpoin 检查点? Checkpoint …...
Jmeter性能测试系列-性能测试需求分析
性能测试需求分析 性能测试需求分析与传统的功能测试需求有所不同,功能测试需求分析重点在于从用户层面分析被测对象的功能性、易用性等质量特性,性能测试则需要从终端用户应用、系统架构设计、硬件配置等多个纬度分析系统可能存在性能瓶颈的业务。 性…...

Syncfusion Essential Studio JavaScrip Crack
Syncfusion Essential Studio JavaScrip Crack 数据透视表 添加了在将数据透视表导出到PDF文档时自定义列宽的支持。 签名 添加了对在特定位置绘制文本的支持。 Syncfusion Essential Studio for JavaScript在一个包中包含80多个高性能、轻量级、模块化和响应式UI组件。包括Jav…...

8.13黄金是否进入下行通道?下周开盘如何布局
近期有哪些消息面影响黄金走势?黄金多空该如何研判? 黄金消息面解析:周五(8月11日)现货黄金小幅收低,受累于美元走强和美国国债收益率上升,本周录得6月底以来最差单周表现。投资者在评估最新一批通胀报告和消费者信…...
Idea的基本使用带案例---详细易懂
一.idea是什么 有专业人士说,idea是天生适合做微软,当时我还想肯定是夸大其词了,但当你用起来的时候确实很爽,😊😊 ntelliJ IDEA是一种集成开发环境(IDE),由JetBrains开发…...
)
uniapp 对接腾讯云IM群组成员管理(增删改查)
UniApp 实战:腾讯云IM群组成员管理(增删改查) 一、前言 在社交类App开发中,群组成员管理是核心功能之一。本文将基于UniApp框架,结合腾讯云IM SDK,详细讲解如何实现群组成员的增删改查全流程。 权限校验…...

模型参数、模型存储精度、参数与显存
模型参数量衡量单位 M:百万(Million) B:十亿(Billion) 1 B 1000 M 1B 1000M 1B1000M 参数存储精度 模型参数是固定的,但是一个参数所表示多少字节不一定,需要看这个参数以什么…...

【解密LSTM、GRU如何解决传统RNN梯度消失问题】
解密LSTM与GRU:如何让RNN变得更聪明? 在深度学习的世界里,循环神经网络(RNN)以其卓越的序列数据处理能力广泛应用于自然语言处理、时间序列预测等领域。然而,传统RNN存在的一个严重问题——梯度消失&#…...

蓝桥杯 2024 15届国赛 A组 儿童节快乐
P10576 [蓝桥杯 2024 国 A] 儿童节快乐 题目描述 五彩斑斓的气球在蓝天下悠然飘荡,轻快的音乐在耳边持续回荡,小朋友们手牵着手一同畅快欢笑。在这样一片安乐祥和的氛围下,六一来了。 今天是六一儿童节,小蓝老师为了让大家在节…...

376. Wiggle Subsequence
376. Wiggle Subsequence 代码 class Solution { public:int wiggleMaxLength(vector<int>& nums) {int n nums.size();int res 1;int prediff 0;int curdiff 0;for(int i 0;i < n-1;i){curdiff nums[i1] - nums[i];if( (prediff > 0 && curdif…...

vue3 字体颜色设置的多种方式
在Vue 3中设置字体颜色可以通过多种方式实现,这取决于你是想在组件内部直接设置,还是在CSS/SCSS/LESS等样式文件中定义。以下是几种常见的方法: 1. 内联样式 你可以直接在模板中使用style绑定来设置字体颜色。 <template><div :s…...

Mac软件卸载指南,简单易懂!
刚和Adobe分手,它却总在Library里给你写"回忆录"?卸载的Final Cut Pro像电子幽灵般阴魂不散?总是会有残留文件,别慌!这份Mac软件卸载指南,将用最硬核的方式教你"数字分手术"࿰…...

BCS 2025|百度副总裁陈洋:智能体在安全领域的应用实践
6月5日,2025全球数字经济大会数字安全主论坛暨北京网络安全大会在国家会议中心隆重开幕。百度副总裁陈洋受邀出席,并作《智能体在安全领域的应用实践》主题演讲,分享了在智能体在安全领域的突破性实践。他指出,百度通过将安全能力…...

重启Eureka集群中的节点,对已经注册的服务有什么影响
先看答案,如果正确地操作,重启Eureka集群中的节点,对已经注册的服务影响非常小,甚至可以做到无感知。 但如果操作不当,可能会引发短暂的服务发现问题。 下面我们从Eureka的核心工作原理来详细分析这个问题。 Eureka的…...

AI病理诊断七剑下天山,医疗未来触手可及
一、病理诊断困局:刀尖上的医学艺术 1.1 金标准背后的隐痛 病理诊断被誉为"诊断的诊断",医生需通过显微镜观察组织切片,在细胞迷宫中捕捉癌变信号。某省病理质控报告显示,基层医院误诊率达12%-15%,专家会诊…...
