面试热题(全排列)
给定一个不含重复数字的整数数组
nums,返回其 所有可能的全排列 。可以 按任意顺序 返回答案。输入:nums = [1,2,3] 输出:[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]
先在这里说明一下排列和组合的区别?
组合:是指从一个元素集合中选择出若干个元素,形成一个无序的子集,组合不考虑元素的顺序,只关注元素的选择
排列:是指从一个元素集合中选择出若干元素,形成一个有序的序列。排列关注元素的顺序。
简单的来说,就是排列是元素是有序的,组合是无序的
一般排列组合问题我们都可以看成是一棵树(每个元素不允许重复)
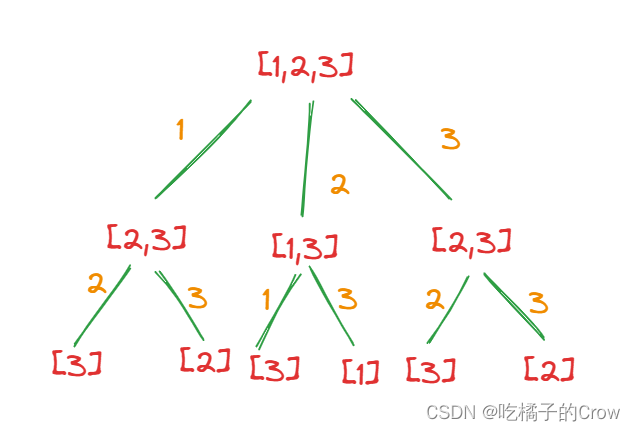
因为我们这题要求的是不重复的排列数,所以我们的模板就可以套了(模板必须要记的——理解)
//不含重复元素的排列数
void backTrack(int[] nums){1for(int i=0;i<nums.length;i++){if(uesd[i])continue;used[i]=true;path.addLast(nums[i]);backTrack(nums);path.removeLast(nums[i]);used[i]=false;}源代码如下:
//存储结果集List<List<Integer>> list = new ArrayList<>();//路径Deque<Integer> path = new LinkedList<>();//是否被访问boolean[] visited = null;public List<List<Integer>> permute(int[] nums) {//对入参进行判断if (nums == null || nums.length == 0) {return list;}//对数组进行初始化visited=new boolean[nums.length];//开始递归,因为是排列,后面的元素也有可能在前面的元素前面,所以不需要传递索引backtracking(nums);//返回结果集return list;}private void backtracking(int[] nums) {//找到满足条件得到一种情况,存入结果集中if (path.size()== nums.length) {list.add(new ArrayList<>(path));return;}//遍历每一个元素for (int j = 0; j < nums.length; j++) {//如果被访问过,直接跳过,避免重复选择if(visited[j]){continue;}path.add(nums[j]);visited[j]=true;backtracking(nums);//回溯path.removeLast();visited[j]=false;}
}在这里给大家提供我刷组合排列问题总结的模板:
组合子集问题每个元素的相对位置已经固定,所以每次去枚举的时候都是从自身的右侧开始枚举
排列问题的每个元素的相对位置是不固定的。左侧的元素可能会出现在右侧,故每次每次枚举都是从0位置上开始枚举的
-
元素无重不可复选(nums中的元素唯一,每个元素最多只能被使用一次)
/*组合/子集问题回溯模板*/
/* [1,2,3] */
void backTrack(int[] nums,int start){//顺序无关,每次从自身的右边开始for(int i=start;i<nums.length;i++){path.addLast(nums[i]);backTrack(nums,i+1);path.removeLast(nums[i]);}
}
/* 排列问题回溯模板*/
void backTrack(int[] nums){//顺序有关,每次从0开始for(int i=0;i<nums.length;i++){if(uesd[i])continue;used[i]=true;path.addLast(nums[i]);backTrack(nums);path.removeLast(nums[i]);used[i]=false;}
}-
.元素可重不可复选(nums中的元素可以存在重复,每个元素最多只能被使用一次)
Arrays.sort(nums); /* 组合/子集问题回溯算法框架 */ void backtrack(int[] nums, int start) {// 回溯算法标准框架for (int i = start; i < nums.length; i++) {// 剪枝逻辑,跳过值相同的相邻树枝if (i > start && nums[i] == nums[i - 1]) {continue;}// 做选择track.addLast(nums[i]);// 注意参数backtrack(nums, i + 1);// 撤销选择track.removeLast();} }Arrays.sort(nums); /* 排列问题回溯算法框架 */ void backtrack(int[] nums) {for (int i = 0; i < nums.length; i++) {// 剪枝逻辑if (used[i]) {continue;}// 剪枝逻辑,固定相同的元素在排列中的相对位置if (i > 0 && nums[i] == nums[i - 1] && !used[i - 1]) {continue;}// 做选择used[i] = true;track.addLast(nums[i]);backtrack(nums);// 撤销选择track.removeLast();used[i] = false;} }
有很多人对上述剪枝操作不理解,看了这幅图你就会豁然开
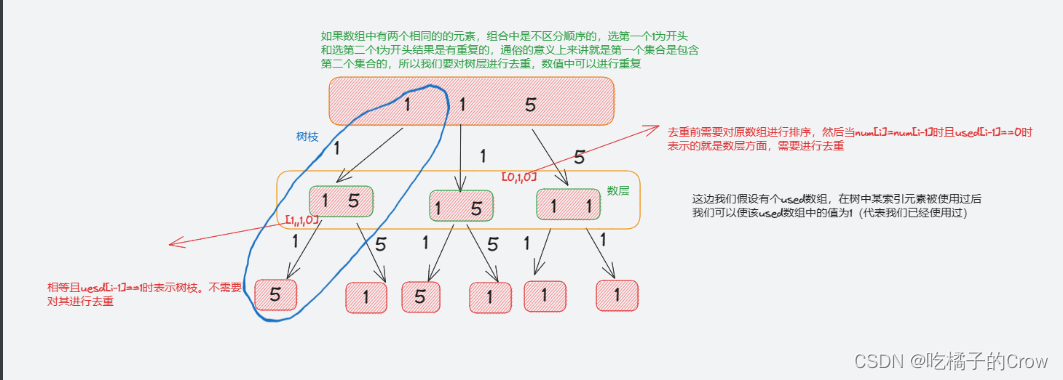
-
元素无重可复选(nums中的元素都是唯一的,每个元素可以被使用若干次)
/* 组合/子集问题回溯算法框架 */ void backtrack(int[] nums, int start) {// 回溯算法标准框架for (int i = start; i < nums.length; i++) {// 做选择track.addLast(nums[i]);// 可以复选,所以i不用+1作为参数backtrack(nums, i);// 撤销选择track.removeLast();} }/* 排列问题回溯算法框架 */ void backtrack(int[] nums) {for (int i = 0; i < nums.length; i++) {// 做选择track.addLast(nums[i]);backtrack(nums);// 撤销选择track.removeLast();} }
相关文章:

面试热题(全排列)
给定一个不含重复数字的整数数组 nums ,返回其 所有可能的全排列 。可以 按任意顺序 返回答案。 输入:nums [1,2,3] 输出:[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]] 先在这里说明一下排列和组合的区别? 组合:是指从一…...

一文走进时序数据库性能测试工具 TSBS
一、背景 在物联网、车联网等时序数据场景中,数据的高速写入能力至关重要,会对产品方案的可用性、可靠性和扩展性产生影响。 以物联网为例,当面临千万甚至上亿设备、平均每个设备采集几十个到几百个指标时,每秒生成的数据将达到…...
通俗讲解-动量梯度下降法原理与代码实例
本站原创文章,转载请说明来自《老饼讲解-BP神经网络》bp.bbbdata.com 目录 一.动量梯度下降法介绍 1.1 动量梯度下降法简介与思想 1.2 动量梯度下降法的算法流程 二.动量梯度下降法代码实例 2.1 动量梯度下降法实例代码 一.动量梯度下降法介绍…...
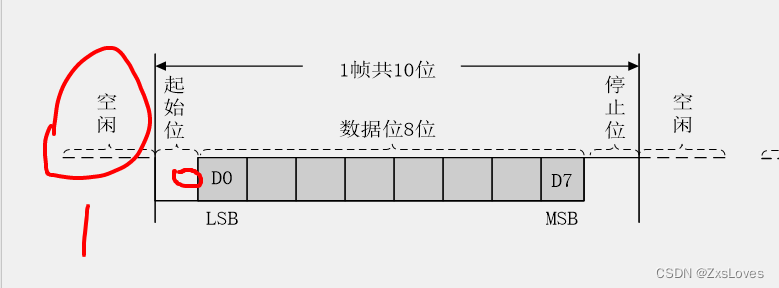
【【STM32-USART串口协议】】
STM32-USART串口协议 USART串口协议 •通信的目的:将一个设备的数据传送到另一个设备,扩展硬件系统 •通信协议:制定通信的规则,通信双方按照协议规则进行数据收发 就是我们并不能在芯片上设计完全部的一下子完成所有的设计&…...

vue3.0组件通信
1、props 没有加TS限制类型的时候 1. 数组写法 defineProps([count, changCount]) 2. 对象写法 defineProps({count: Number,changCount: Function }) 3. 配置对象 defineProps({count: {type: Number,default: 2},changCount: {type: Function,required: true} })注意: defi…...

费曼学习法
费曼学习法 费曼学习法(Feynman Technique)是一种学习和理解复杂概念的方法,以理查德费曼(Richard Feynman)这位著名的理论物理学家命名。该方法的核心思想是通过将学习内容简化并用自己的话解释给别人,来…...

Kubernetes介绍和部署,使用
1.k8s kubernetes来自希腊语舵手,google, 8是ubernete 1.管理docker容器 go写的(并发) 2.用于微服务 3.cncf云原生基金会 2.mater(管理节点)和nodes(微服务节点) 3.部署 1.minikube kind官网在线测试语句 2.kubeadm(官方)(安装比较方便 添加) 3.github下载二进制包 4.yum(老) …...
视频汇聚平台EasyCVR视频监控播放平台WebRTC流地址无法播放的问题解决方案
开源EasyDarwin视频监控TSINGSEE青犀视频平台EasyCVR能在复杂的网络环境中,将分散的各类视频资源进行统一汇聚、整合、集中管理,在视频监控播放上,TSINGSEE青犀视频安防监控汇聚平台可支持1、4、9、16个画面窗口播放,可同时播放多…...

node.js 基础高并发案例
什么是高并发 高并发是指系统在同一时间段内需要处理大量的并发请求或同时进行大量的操作。在计算机领域中,高并发通常指的是在短时间内有大量的用户或客户端同时访问系统或进行操作,对系统的并发处理能力提出了较高的要求。 高并发的特点包括 大量的…...
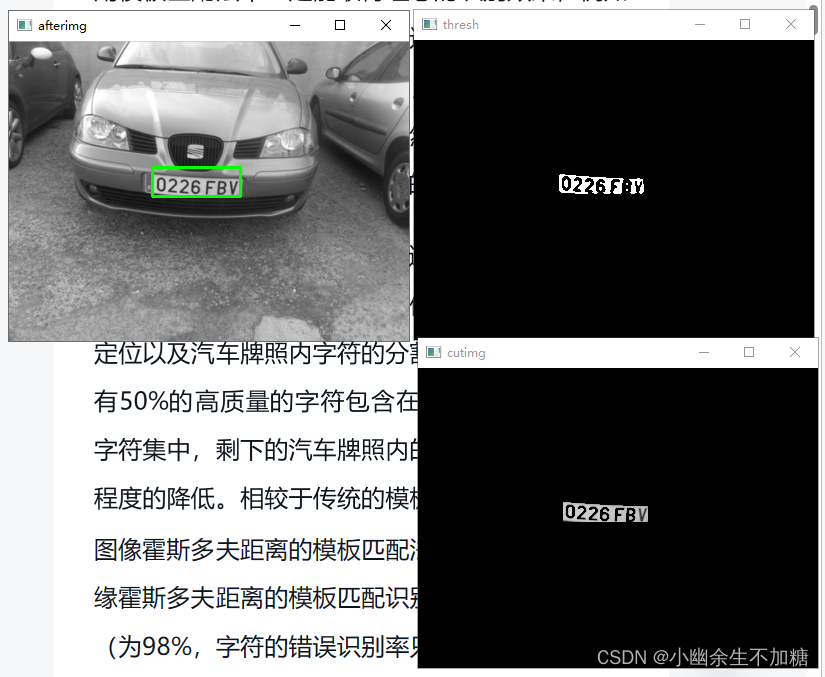
OpenCV实例(八)车牌字符识别技术(二)字符识别
车牌字符识别技术(二)字符识别 1.字符识别原理及其发展阶段2.字符识别方法3.英文、数字识别4.车牌定位实例 1.字符识别原理及其发展阶段 匹配判别是字符识别的基本思想,与其他模式识别的应用非常类似。字符识别的基本原理就是对字符图像进行…...

svn文章五:问题排查与修复 - 出了问题怎么办?SVN故障排除与修复指南
文章五:问题排查与修复 - “出了问题怎么办?SVN故障排除与修复指南” 概述:在使用SVN时,难免会遇到一些问题和错误。在这篇文章中,我们将教您如何进行故障排查和修复,保护您的SVN仓库和数据安全。 1. 引言…...

国产开源ambari之DataSophon部署
介绍 DataSophon致力于快速实现部署、管理、监控以及自动化运维大数据云原生平台,帮助您快速构建起稳定、高效、可弹性伸缩的大数据云原生平台。 主要特性有: 快速部署,可快速完成300个节点的大数据集群部署兼容复杂环境,极少的依赖使其很容易适配各种复杂环境监控指标全面丰…...

面试之快速学习STL- vector
1. vector底层实现机制刨析: 简述:使用三个迭代器表示的:  这也就解释了,为什么 vector 容器在进行扩容后,与其相关的指针、引用以及迭代器可能会失效的原因。 insert 整体向后移 erase 整体向前移…...
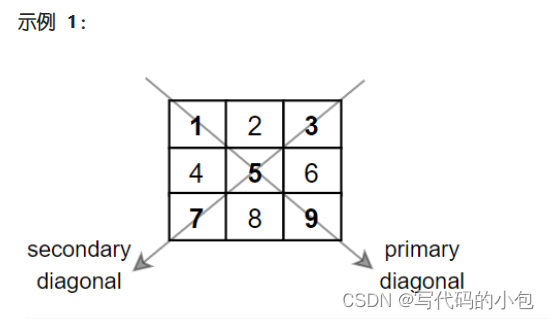
LeetCode_03Java_1572. 矩阵对角线元素的和
给你一个正方形矩阵 mat,请你返回矩阵对角线元素的和。 请你返回在矩阵主对角线上的元素和副对角线上且不在主对角线上元素的和。 输入:mat [[1,2,3],[4,5,6],[7,8,9]] 输出:25 解释:对角线的和为:1 5 9 3 7 2…...

系统架构设计师---职责及与其他角色的关系区别
一. 系统架构设计师的职责如下: 系统架构设计师是系统或产品线的设计责任人,是一个负责理解和管理并最终确认和评估非功能性系统需求(比如软件的可维护性、性能、复用性、可靠性、有效性和可测试性等),给出 开发规范,搭建系统实现的核心构架,对整个软件架构、关键构件、…...
【Visual Studio Code】--- Win11 C盘爆满 修改 Code 插件数据和缓存的保存路径
Win11 C盘爆满 修改 Code 插件数据和缓存的保存路径 一、概述二、修改 Code 插件数据和缓存的保存路径 一、概述 一个好的文章能够帮助开发者完成更便捷、更快速的开发。书山有路勤为径,学海无涯苦作舟。我是秋知叶i、期望每一个阅读了我的文章的开发者都能够有所成…...

mapbox-gl中mvt、pbf 矢量切片 feature id bug
1.版本:mapbox-gl.js 2.13.0,pbf采用 postgis生成 2.调用矢量切片时,采用如下方法查询矢量切片要素,报错 map.on(mousemove, function(e) { var bbox = [ [e.point.x - 5, e.point.y - 5], [e.point…...

206、仿真-51单片机锂电池蓄电池电压电流加按键控制开关状态Proteus仿真设计(程序+Proteus仿真+配套资料等)
毕设帮助、开题指导、技术解答(有偿)见文未 目录 一、硬件设计 二、设计功能 三、Proteus仿真图 四、程序源码 资料包括: 需要完整的资料可以点击下面的名片加下我,找我要资源压缩包的百度网盘下载地址及提取码。 方案选择 单片机的选择 方案一&a…...
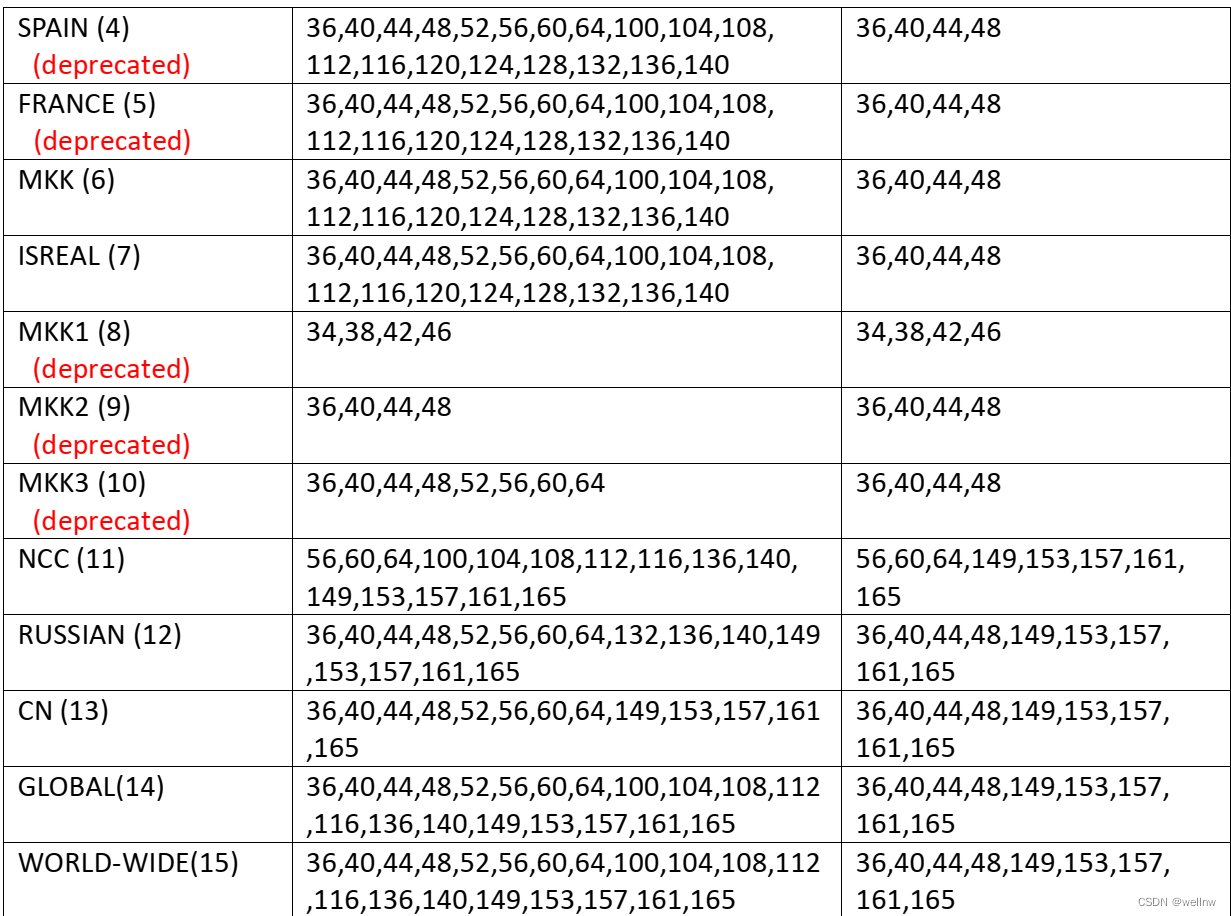
【Realtek sdk-3.4.14b】RTL8197F+RTL8812F欧洲屏蔽5G天气雷达信道DFS信道120、124、128方法
需求描述 对于欧洲国家来说,默认支持DFS信道,但是有三个信道比较特殊,是天气雷达信道,如下图所示120、124、128,天气雷达信道有个特点就是在信号可以发射之前需要检测静默15min,如果信道自动选择到了天气雷达信道,就会有15min的时间无法连接到WiFi热点,严重影响用户体验…...
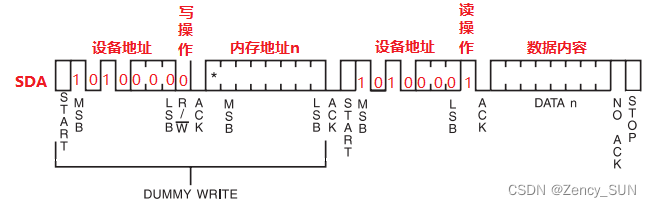
【嵌入式学习笔记】嵌入式入门7——IIC总线协议
1.IIC简介 IIC即Inter Integrated Circuit,集成电路总线,是一种同步,串行,半双工通信总线。 IIC总线协议——总线就是传输数据通道,协议就是传输数据的规则,有以下特点: 由时钟线SCL和数据线S…...

Spark 之 入门讲解详细版(1)
1、简介 1.1 Spark简介 Spark是加州大学伯克利分校AMP实验室(Algorithms, Machines, and People Lab)开发通用内存并行计算框架。Spark在2013年6月进入Apache成为孵化项目,8个月后成为Apache顶级项目,速度之快足见过人之处&…...

简易版抽奖活动的设计技术方案
1.前言 本技术方案旨在设计一套完整且可靠的抽奖活动逻辑,确保抽奖活动能够公平、公正、公开地进行,同时满足高并发访问、数据安全存储与高效处理等需求,为用户提供流畅的抽奖体验,助力业务顺利开展。本方案将涵盖抽奖活动的整体架构设计、核心流程逻辑、关键功能实现以及…...

线程同步:确保多线程程序的安全与高效!
全文目录: 开篇语前序前言第一部分:线程同步的概念与问题1.1 线程同步的概念1.2 线程同步的问题1.3 线程同步的解决方案 第二部分:synchronized关键字的使用2.1 使用 synchronized修饰方法2.2 使用 synchronized修饰代码块 第三部分ÿ…...

vscode(仍待补充)
写于2025 6.9 主包将加入vscode这个更权威的圈子 vscode的基本使用 侧边栏 vscode还能连接ssh? debug时使用的launch文件 1.task.json {"tasks": [{"type": "cppbuild","label": "C/C: gcc.exe 生成活动文件"…...

LeetCode - 394. 字符串解码
题目 394. 字符串解码 - 力扣(LeetCode) 思路 使用两个栈:一个存储重复次数,一个存储字符串 遍历输入字符串: 数字处理:遇到数字时,累积计算重复次数左括号处理:保存当前状态&a…...

渲染学进阶内容——模型
最近在写模组的时候发现渲染器里面离不开模型的定义,在渲染的第二篇文章中简单的讲解了一下关于模型部分的内容,其实不管是方块还是方块实体,都离不开模型的内容 🧱 一、CubeListBuilder 功能解析 CubeListBuilder 是 Minecraft Java 版模型系统的核心构建器,用于动态创…...

C++ 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

「全栈技术解析」推客小程序系统开发:从架构设计到裂变增长的完整解决方案
在移动互联网营销竞争白热化的当下,推客小程序系统凭借其裂变传播、精准营销等特性,成为企业抢占市场的利器。本文将深度解析推客小程序系统开发的核心技术与实现路径,助力开发者打造具有市场竞争力的营销工具。 一、系统核心功能架构&…...

认识CMake并使用CMake构建自己的第一个项目
1.CMake的作用和优势 跨平台支持:CMake支持多种操作系统和编译器,使用同一份构建配置可以在不同的环境中使用 简化配置:通过CMakeLists.txt文件,用户可以定义项目结构、依赖项、编译选项等,无需手动编写复杂的构建脚本…...
:LSM Tree 概述)
从零手写Java版本的LSM Tree (一):LSM Tree 概述
🔥 推荐一个高质量的Java LSM Tree开源项目! https://github.com/brianxiadong/java-lsm-tree java-lsm-tree 是一个从零实现的Log-Structured Merge Tree,专为高并发写入场景设计。 核心亮点: ⚡ 极致性能:写入速度超…...
